第四章 矩阵的标准型PPT幻灯片

称 J 为 A 的Jordan标准型。并称方阵
i
Ji (i )
1
i O
O
1
, i 1,2,L,s
i mimi
为 m i 阶Jordan 块。
数学系 李继根（jgli@）
定理 2 设 ACnn。如果 A 的特征多项式可
分解因式为 () ( 1 ) m 1 L (s ) m s
数学系 李继根（jgli@）
§1、矩阵的Jordan标准型
由于一般矩阵与对角矩阵不相似，因此我 们“退而求其次”，寻找“几乎对角的” 矩阵。这就引出了矩阵在相似下的各种标 准型问题，其中Jordan标准型是最接近 对角的矩阵，只在第1条对角线上取1或0。 弄清楚了矩阵相似的本质，理论上、计算 上以及应用上的许多问题就容易处理了， 当然花费也大了。
2 1 1 1
A
2
1
3
2
1 1 0 1
1
1
2
2
数学系 李继根（jgli@）
解： A 的特征值为 `1 0 ,`2`3`4 1 ，则
JA
A1(2)
A2(1)
因为特征值 `1 0 为单根，所以 A1(0) 0
并从 (A0I)x解得对应的特征向量为
1(1,3,1,2)T
数学系 李继根（jgli@）
最后，由可逆线性变换 x P y 得原方程组的解
xx12
c2et c3t et 2c2et c3(2t
1)et
x3 c1e2t c2et c3(t 1)et
数学系 李继根（jgli@）
例 5 现代控制理论中，线性定常系统(Linear time
i
阶的Jordan子矩阵，有 k
个
i
阶数为 n i j ( n i 1 n i 2 L n i k i n i ) 的
Jordan块，即 A i ( i ) d i a g ( J 1 ( i ) , J 2 ( i ) , L , J k i ( i ) )
数学系 李继根（jgli@）
JA A1(2)
A2(1)
因为特征值 `1 2 为单根，所以 A1(2) 2
并从 (A2I)x解得对应的特征向量为
1 (1,2,4)T
数学系 李继根（jgli@）
对于二重特征值 `2,3 1 ，由 (AI)x
只解得唯一的特征向量为
2 (1,1,1)T
因此 A 2 ( 1 ) 中只有一个Jordan块，即
根据 J A 的结构，将Jordan变换矩阵 P 列分块为
P (p 1 ,p 2 ,L ,p t) 其中 p i 是 n n i 阶的矩阵。 由 APPJA ，可知
A p i p iA i(i)( i 1 ,2 ,L ,t)
数学系 李继根（jgli@）
进一步，根据 A i ( i ) 的结构，将 p i 列分块为
这里 x(x 1,x 2,x 3)T ,d d x t(d d x t1,d d x t2,d d x t3)T ,
1 1 0
A
4
3
0
1 0 2
数学系 李继根（jgli@）
由上例，存在可逆线性变换 x P y 使得
P1APJA
其中
0 1 0
2 0 0
P0 2 1, JA0 1 1
二、 Jordan标准型的一种简易求法
把 A 的同一个特征值的若干个Jordan块排列在一起，
就得到Jordan标准型 J A d i a g ( A 1 ( 1 ) , A 2 ( 2 ) , L , A t ( t ) )
(n 1 n 2 L n t n )
其中 A i ( i ) 是 n
数学系 李继根（jgli@）
第四章 矩阵的标准型
数学系 李继根（jgli@）
标准型的理论源自矩阵的相似性，因为相 似矩阵有许多相似不变量：特征多项式、特征 值（包括代n 数重数和几何重数）、行列式、迹 及秩等，并且特征向量也可以借助于可逆的相 似变换矩阵互相求出。这自然导出了寻找相似 矩阵集合中的“代表矩阵”的问题。“代表矩 阵”当然越简单越好。对于可对角化矩阵， “代表矩阵”就是特征值组成的对角矩阵。特 别地，对于正规矩阵，可逆的相似变换矩阵特 殊化为酉矩阵或正交矩阵。但是令人非常遗憾 的是：一般矩阵未必与对角矩阵相似！！！
2 (1,2,1)T
对重根有几个特 征向量，就有几 个约旦块
因此 A 2 ( 1 ) 中只有一个Jordan块，即
1 1
A2
(1)
0
1
求解 (AI)2，可得所需的广义特征向量
(0,1,1)T
数学系 李继根（jgli@）
综合上述，可得
0 1 0
2 0 0
P0 2 1, JA0 1 1
其中， pi(1 j)(j1 ,2,L,ki)是矩阵 A 关于特征
值 i 的一个特征向量，
的广义特征向量,称
p
( i
n j
i
j
)
pi(2j),L,
为 i 的
p(ni j ) 则称为 ij
n i j 级根向量。
i
数学系 李继根（jgli@）
当所有的 n i j 1 时，可知 k i n i ，此时矩阵没
invariant , LTI )的状态空间描述为
x& Ax Bu
y
Cx
Du
这里矩阵 A 表示了系统内部状态变量之间的联系，
称为系统矩阵；矩阵 B 称为输入矩阵或控制矩阵；
矩阵 C 称为输出矩阵或观测矩阵；矩阵 D 称为直
接观测矩阵。
数学系 李继根（jgli@）
做可逆线性变换 x& P x ，则
1 1
A2(1)
0
1
求解 (AI)2，可得所需的广义特征向量
(1,0,1)T
数学系 李继根（jgli@）
综合上述，可得
1 1 1
2 0 0
P2 1 0, JA0 1 1
4 1 1
0 0 1
1 2 1
P
1
1 9
2
6
5 3
2
3
数学系 李继根（jgli@）
n 1
n 2
n t
即矩阵 A 是可对角化矩阵。显然正规矩阵是一类最
特殊的可对角化矩阵。
数学系 李继根（jgli@）
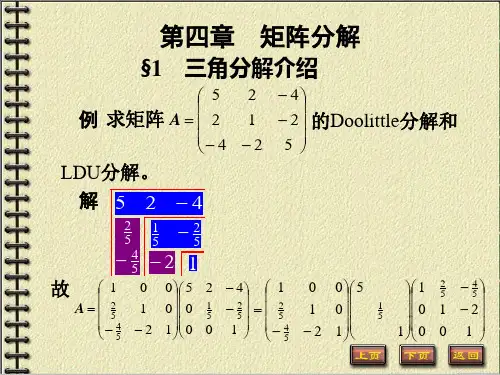
例 3 求矩阵 A 的 Jordan标准型 J A 和相应的
Jordan变换矩阵 P ，其中
1 1 0
A
4
3
0
1 0 2
数学系 李继根（jgli@）
求下列状态方程的约当标准型：
0 1 0 0 x&AxBu0 0 1x0u
2 3 0 1
这里矩阵 A 是特征多项式 | I A|的友矩阵。
数学系 李继根（jgli@）
解：|I A | 3 3 2 ( 2 ) ( 1 ) 2 0
A 的特征值为 `12, `2`31，故设
解： A
特征值为 `12,`2`31，所以设
JA
A1(2)
A2(1)
因为特征值 `1 2 为单根，所以 A1(2) 2
并从 (A2I)x解得对应的特征向量为
1 (0,0,1)T
数学系 李继根（jgli@）
对于二重特征值 `2 `3 1 ，由 (AI)x
只解得唯一的特征向量为
最后，根据 J j ( i ) 的结构，设
p ij (p i(1 j),p i(2 j),L ,p i(n jij))
由 A pij pijJj( i)，可知
(
A
i
I
)
p
( i
1 j
)
(
A
iI
)
p
( i
2 j
)
p
( i
1 j
)
L
(
A
iI
)
p ( ni j ) ij
p ( ni j 1) ij
因此经过可逆线性变换 x& P x 后，系统矩阵 A 和
控制矩阵 B 分别为
2 0 0
A P1AP0 1
1
J
0 0 1
2
B
P 1B
1 9
1
.
1
数学系 李继根（jgli@）
例 6 求矩阵 A 的 Jordan标准型 J A 和相应的
Jordan变换矩阵 P ，其中
则 V 可分解成不变子空间的直和
V N 1 排 N 2L ? N s
这里 N iK er((T iE )m i)
数学系 李继根（jgli@）
适当选取每个子空间 N i 的基（称为Jordan基）， 则每个子空间的Jordan基合并起来即为 V 的Jordan
基，并且 V 在该Jordan基下的矩阵为块对角阵 J d i a g ( J 1 ( 1 ) , J 2 ( 2 ) , L , J s ( s ) )
1 1 1
0 0 1
数学系 李继根（jgli@）
例 4 用 Jordan标准型理论求解线性微分方程组
d x1 dt
x1
x2
d d
x2 t
4 x1
3 x2
d x3 dt
x1
2 x3
数学系 李继根（jgli@）
解： 方程组的矩阵形式为
dx Ax dt
p i (p i1 ,p i2 ,L ,p ik i)
其中
p ij(j 1 ,2 ,L ,k i)是 n ni
阶矩阵。
j
由 Api piA i(i) ，可知
A p i j p i j J j ( i )( j 1 , 2 , L , k i )
数学系 李继根（jgli@）