大工14春《高层建筑结构》辅导资料十一
- 格式:doc
- 大小:2.27 MB
- 文档页数:12

高层结构施工复习资料高层结构施工复习资料一、引言高层结构施工是建筑工程中一项重要的环节,涉及到建筑物的稳定性和安全性。
在施工过程中,需要考虑多个因素,包括结构设计、材料选择、施工方法等。
本文将对高层结构施工的相关知识进行复习和总结,以便读者对该领域有更深入的了解。
二、结构设计高层建筑的结构设计是确保建筑物能够承受外部荷载和内部力的重要因素。
常见的高层建筑结构形式包括框架结构、筒体结构和剪力墙结构等。
框架结构是最常见的一种形式,由柱、梁和楼板组成,能够承受垂直和水平荷载。
筒体结构则是通过建筑物的外壳来承受荷载,适用于曲线形状的建筑。
剪力墙结构则通过设置墙体来承受水平荷载,适用于地震区域。
在结构设计中,还需要考虑建筑物的抗震性能。
抗震设计是为了保证建筑物在地震发生时能够保持稳定,减少损坏和倒塌的风险。
常见的抗震设计措施包括增加结构的刚度、设置剪力墙和加固柱子等。
三、材料选择在高层结构施工中,材料的选择对建筑物的稳定性和安全性有着重要影响。
常见的结构材料包括钢筋混凝土、钢结构和预应力混凝土等。
钢筋混凝土是最常用的结构材料之一,具有良好的抗压和抗拉强度。
在高层建筑中,钢筋混凝土常用于柱子、梁和楼板等部位。
钢结构则具有较高的强度和刚度,适用于大跨度的建筑。
预应力混凝土则通过在混凝土中设置预应力钢筋来提高结构的抗拉能力,适用于需要较大荷载的建筑。
四、施工方法高层结构施工需要采用合适的施工方法,以确保施工过程的安全和高效。
常见的施工方法包括顶升法、模板支撑法和悬挂脚手架法等。
顶升法是一种常用的施工方法,适用于大型建筑物的施工。
该方法通过设置临时支撑和液压顶升设备,将建筑物逐层顶升,以便进行下层结构的施工。
模板支撑法则是通过设置模板和支撑来进行楼板的施工。
悬挂脚手架法则是通过悬挂脚手架来进行外墙的施工。
五、施工安全高层结构施工的安全性是至关重要的。
在施工过程中,需要采取一系列安全措施,以确保工人和建筑物的安全。
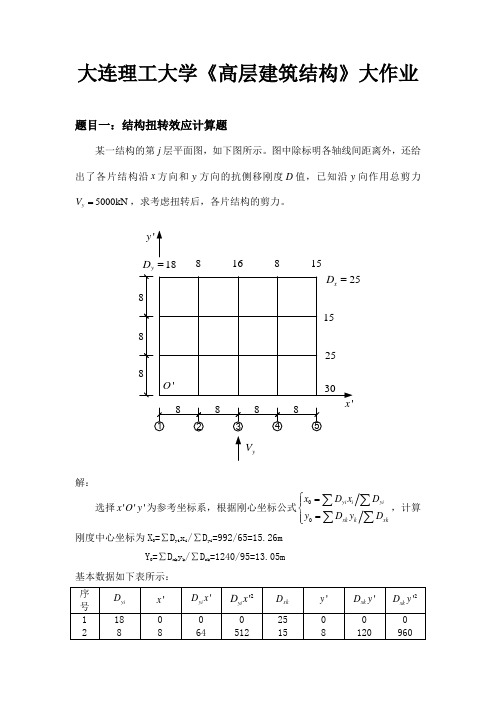
大连理工大学《高层建筑结构》大作业题目一:结构扭转效应计算题某一结构的第j 层平面图,如下图所示。
图中除标明各轴线间距离外,还给出了各片结构沿x 方向和y 方向的抗侧移刚度D 值,已知沿y 向作用总剪力5000kN y V =,求考虑扭转后,各片结构的剪力。
'yyV 18y D 816815888解:选择'''x O y 为参考坐标系,根据刚心坐标公式00yi iyi xk kxkx D x Dy D y D⎧=⎪⎨=⎪⎩∑∑∑∑,计算刚度中心坐标为X 0=∑D yi x i /∑D yi =992/65=15.26mY 0=∑D xk y k /∑D xk =1240/95=13.05m基本数据如下表所示:以刚度中心为原点,建立坐标系统D xO y 。
因为0'y y y =-,0'xkxk Dy y D =∑∑,所以∑D xk y 2=24640-13.05*13.05*95=8461 同理可得:∑D yi x 2=24576-15.26*15.26*65=9440根据公式可得a yi =1+65*0.74/(8461+9440)*x i =1+0.00269*x i各片结构的y α值为x 1=-15.26 a y1=1-0.00269*15.26=0.959 x 2=-7.26 a y2=1-0.00269*7.26=0.980 x 3=-0.74 a y3=1+0.00269*0.74=1.002 x 4=-8.74 a y4=1+0.00269*8.74=1.024 x 5=-16.74 a y5=1+0.00269*16.74=1.045由此可以计算各片结构承担的剪力值 v y1=0.959*18/65*5000=1327.8KN v y2=0.980*8/65*5000=603.1KN v y3=1.002*16/65*5000=1233.2KN v y4=1.024*8/65*5000=630.2KN v y5=1.045*15/65*5000=1205.8KN题目三:计算水平地震作用有哪些方法?适用于什么样的建筑物?答:计算水平地震作用的具体方法分为反应谱底部剪力法和反应谱振型分解法。

第一章1,《高层建筑混凝土结构技术规程》将10层及10层以上或高度超过28m的钢筋混凝土结构称为高层建筑结构。
当建筑高度超过100m时,称为超高层建筑。
《民用建筑设计通则》、《高层民用建筑设计防火规范》将10层及10层以上的住宅建筑与高度超过24m的公共建筑和综合性建筑称为高层建筑。
建筑高度:建筑高度指建筑物室外地而到其檐口或屋而屋而板板顶的高度,屋顶上的瞭望塔、水箱间、电梯机房、排烟机房和出屋面的楼梯间等不计入建筑高度和层数内。
第二章1,H前高层建筑结构的结构形式按材料区分,主要有砌体结构,钢筋混凝土结构,钢结构和混合结构四种。
2,常见的结构体系A,框架结构体系B,剪力墙结构体系C,框架剪力墙或框架筒体结构体系及框架支撑结构D,筒体结构体系E,框架■核心筒结构体系。
4但由于框筒的筒壁是网络式的结构,使得腹板框架和翼缘框架中的各柱的轴力分布不均匀,角柱的轴力大,中柱的轴力小,这种现象称为剪力滞后。
5,结构的总体布置包括结构的平面布置和竖向布置。
结构平面布置的原则为:(1)对高层建筑的每一个独立单元,宜使结构平面布置简单、规则和对称,结构的抗侧力结构和刚度分布力求均匀;(2)宜选择风压较小的建筑平而体型,并注意邻近高层建筑对该风压分布的影响;(3)选择有利于抗震的结构平而;(4)避免在建筑物的两端或拐角部位设置电梯间或楼梯间,以避免削弱这些受力集屮或易产生扭转变形的部位的楼板刚度;(5)选用合理的楼盖形式。
P18 沉降缝、伸缩缝和防震缝统称为变形缝。
7,宜考虑设置沉降缝的情况:(1)建筑主体结构高度悬殊,重量差别过人;(2)地基不均匀;(3)同一建筑结构不同的单元采用不同基础形式;(4)上部结构采用不同的结构形式或结构体系的交接处。
P198,不设置沉降缝而可供采取的有效措施主耍有:(1)结构全部采用桩基,桩支撑在基岩上;或采用减小沉降的有效措施,并经计算使沉降差控制在允许范围内;(2)主楼与裙房采用不同的基础形式,调整地基土压力使两者沉降基木接近;(3)当地基承载力高, 沉降计算较为可靠时,预昭沉降差,施工时葫将主楼和裙房的基础分开,先施工主楼,后施工裙房,使最后沉降值接近。

高层建筑结构辅导资料九主题:第四章高层建筑结构近似算法(第2.2—2.3节)学习时间:2014年5月26日--6月1日内容:这周我们将学习第四章中的第2.2—2.3节,这部分主要介绍框架结构在水平荷载作用下的内力计算方法(即反弯点法和D值法)以及框架结构变形及稳定验算,下面整理出的框架供同学们学习,希望能够帮助大家更好的学习这部分知识。
一、学习要求1、掌握框架结构在水平荷载作用下的内力计算(反弯点法、D值法);2、掌握框架结构变形及稳定验算。
二、主要内容(一)反弯点法适于各层结构较均匀(层高、梁线刚度变化不大)、节点梁柱线刚度比大于3的多层框架。
1、基本假定(1)柱间剪力分配时认为梁柱线刚比无限大;(2)除底层,柱受力后上下端的转角相等;(3)梁端弯矩可由节点平衡条件求出。
按以上假定,确定反弯点高度、侧移刚度、反弯点处剪力以及杆端弯矩。
2、反弯点高度反弯点高度:反弯点至该层柱底距离。
如下图1所示。
对于上层各柱,由于柱上下端转角及端弯矩相等,故反弯点在柱中央;对于底层柱,由于柱子下端转角为零,上端弯矩小,所以反弯点上移,取2/3柱高处。
P PP 32H 22H 13H 12H 32H 22H图1 反弯点位置图3、侧移刚度D侧移刚度D 的定义:柱端有单位侧移时在柱中产生的剪力值大小,定义为柱子的侧移刚度。
在计算柱子侧移刚度时,按横梁刚度为无限大,则各柱端转角为零,由位移方程可求得柱的侧移刚度表达式如下:321212ci EI D h h== 式中:h ——某层柱的柱高;c i ——某柱的线刚度。
4、同层各柱反弯点处的剪力计算反弯点处弯矩为零,剪力不为零。
自上而下依次沿每层反弯点处取脱离体。
对顶层取脱离体如下图2所示。
3P 32H 313233图2 顶层脱离体图根据水平力平衡有,可以求得顶层各柱在反弯点处的剪力值如下:313131333j jD V D P D =∆=∑323232333jjD V D P D =∆=∑ 333333333j jD V D P D =∆=∑同理,对顶第二层和底层取脱离体如下图3、4所示。

第一章高层建筑结构概述特别提示:结构-构件概念-计算-构造措施1.我国对高层建筑的分类:我国《高层建筑混凝土结构技术规程》(JGJ3-2010)中规定:10层及10层以上或房屋高度大于28m的住宅建筑和房屋高度大于24m的其他高层民用建筑为高层建筑。
建筑高度超过100m的建筑均为超高层建筑。
2.高层建筑的特点A高层建筑中,水平荷载和地震作用对结构设计起着决定性的作用;B水平位移要给予限制;C动力反应不可低估;D结构轴向变形、剪切变形以及温度、沉降的影响加剧;E轴向变形在水平变形中占重要比例。
F材料用量、工程造价呈抛物线关系增长。
3.建筑物高度与水平荷载效应的关系随着高度增大,位移增加最快(4次方关系),弯矩次之(平方关系),轴力则是高度的线性函数。
4.高层建筑结构受力特点(a) 空间整体作用(b)水平力起控制作用(c)侧向变形必须限制(d)柱、墙的轴向变形影响过大的侧向变形会使人不舒服,影响使用。
过大的侧向变形会使填充墙或建筑装修出现裂缝或损坏,也会使电梯轨道变形。
过大的侧向变形会使主体结构出现裂缝,甚至损坏。
过大的侧向变形会使结构产生附加内力,甚至引起倒塌。
钢结构:优点:强度高、韧性大、抗震性能好、易于加工,能缩短现场施工工期,施工方便。
缺点:用钢量大,造价很高,而且耐火性能差。
深圳地王大厦,(81层,383.95m)北京的京广中心(56层,208m)钢筋混凝土结构:优点:造价较低,材料来源丰富,可浇注成各种复杂断面形状,可以组成多种结构体系;可节省钢材,承载能力较高,经过合理设计,可获得较好的抗震性能。
缺点:构件断面大,占据面间大,自重大广州广东国际大厦(63层,200.18m)底层柱尺寸已达1.8*2.2m组合结构:(1)优点:在钢筋混凝土结构基础上,充分发挥钢结构优良的抗拉性能以及混凝土结构的抗压性能进一步减轻结构重量,提高结构延性(2)类型1)用钢材加强钢筋混凝土构件,钢骨钢筋混凝土构件,钢管钢筋混凝土构件.2)部分抗侧力结构用钢结构,另一部分采用钢筋混凝土结构(或部分采用钢骨钢筋混凝土结构)高层建筑结构的结构体系?基本结构体系:1) 框架体系;2) 剪力墙体系;3) 筒体体系。

高层建筑结构辅导资料十六主题:第六章钢筋混凝土框架结构设计(第4—5节)学习时间:2014年7月14日--7月20日内容:这周我们将学习第六章中的第4—5节,这部分主要介绍钢筋混凝土框架结构框架内力调整及框架梁的设计,下面整理出的框架供同学们学习,希望能够帮助大家更好的学习这部分知识。
一、学习要求1、掌握框架内力调整方法;2、掌握框架梁的抗弯和抗剪承载力计算与构造要求。
二、主要内容(一)框架内力调整进行框架结构抗震设计时,允许在梁端出现塑性铰。
为了便于浇捣混凝土,也往往希望节点处梁的负钢筋放得少些。
对于装配式或装配整体式框架,节点并非绝对刚性,梁端实际弯矩将小于其弹性计算值。
因此,在进行框架结构设计时,一般均对梁端弯矩进行调幅,即人为地减小梁端负弯矩,减小节点附近梁顶面的配筋量。
设某框架梁AB 在竖向荷载作用下,计算出梁端的最大负弯矩分别为AO M 、BO M ,梁跨中最大正弯矩为CO M ,则调幅后梁端弯矩如下式中:β——弯矩调幅系数。
对于现浇框架,可取0.80.9β=;对于装配整体式框架,由于接头焊接不牢或由于节点混凝土灌筑不密实等原因,节点容易产生变形而达不到绝对刚性,框架梁端的实际弯矩比弹性计算值要小,因此,弯矩调幅系数允许取得低一些,一般取0.70.8β=。
梁端弯矩调幅后,在相应荷载作用下的跨中弯矩必将增加,这时应校核梁的静力平衡条件,如下图1所示。
支座弯矩调幅后梁端弯矩A M 、B M 的平均值与跨中调整后的正弯矩C M 之和不应小于按简支梁计算的跨中弯矩值0M 。
图1 支座弯矩调幅必须指出,我国有关规范规定:弯矩调幅只对竖向荷载作用下的内力进行,即水平荷载作用下产生的弯矩不参加调幅,因此,弯矩调幅应在内力组合之前进行。
同时还规定,梁截面设计时所采用的跨中正弯矩不应小于按简支梁计算的跨中弯矩的一半。
(二)框架梁的设计1、框架设计抗震等级我国《建筑抗震设计规范》(GB50011-2010)采用二阶段设计方法。
高层建筑结构辅导资料四主题:第二章高层建筑结构体系与布臵原则(第6节)学习时间:2014年4月21日--4月27日内容:这周我们将学习第二章中的第6节,这部分主要介绍高层建筑结构体系的布臵原则,主要包括:房屋结构的最大适用高度及高宽比限值、结构的平面及竖向布臵要求、变形缝的类型与设臵、不规则结构的类型与确定,另外对高层建筑基础还作了简要介绍。
下面整理出的框架供同学们学习,希望能够帮助大家更好的学习这部分知识。
一、学习要求1、熟悉高层建筑结构总体布臵的原则;2、了解各种结构缝的处理方法;3、了解地基基础选型。
二、主要内容(一)最大适用高度《高层建筑混凝土结构技术规程》(JGJ3-2010)(以下简称高规)划分了A 级高度的高层建筑和B级高度的高层建筑。
A级高度的钢筋混凝土高层建筑是指常规的、一般的建筑,也是目前数量最多,应用最广泛的建筑;B级高度的高层建筑是指较高的、设计上有严格要求高层建筑。
A级、B级高度钢筋混凝土高层建筑的最大适用高度见下表1、2所示。
在学习中应该注意新旧规范的不同,大家在学习时以课件为主。
表1 A级高度钢筋混凝土高层建筑的最大适用高度(m)表2 B级高度钢筋混凝土高层建筑的最大适用高度(m)说明:相比于2002规范,新规范增加了对8度0.3g设防的结构适用高度的要求;A级高度高层建筑中,框架结构高度适当降低,板柱-剪力墙结构高度增大较多。
(二)房屋的高宽比高层建筑的高宽比,是对结构刚度、整体稳定、承载能力和经济合理性的宏观控制。
钢筋混凝土高层建筑结构的高宽比不宜超过下表3的规定。
表3 钢筋混凝土高层建筑结构适用的高宽比说明:相比于2002规范,新规范将A级高度与B级高度的适用高宽比限值进行了合并处理,不再强调“最大高宽比”概念;将筒中筒结构和框架-核心筒结构的高宽比限值分开规定,适当提高了筒中筒结构的适用高宽比。
(三)高层建筑结构抗震等级抗震设计的钢筋混凝土高层建筑结构,根据设防烈度、结构类型、房屋高度区分为不同的抗震等级,采用相应的计算和构造措施。
高层建筑结构辅导资料十三主题:第五章扭转近似计算(第1—2节)学习时间:2014年6月23日--6月29日内容:这周我们将学习第五章中的第1—2节,这部分主要介绍高层建筑结构的扭转近似计算方法,包括结构的质量中心(质心)、结构的抗侧移刚度中心(刚心)以及扭转偏心矩的计算方法,下面整理出的框架供同学们学习,希望能够帮助大家更好的学习这部分知识。
一、学习要求1、了解高层建筑结构的扭转近似计算方法;2、掌握结构质心、刚心以及扭转偏心矩的计算方法。
二、主要内容(一)扭转近似计算概述前面介绍了框架结构、剪力墙结构以及框架—剪力墙结构在水平荷载作用下,结构的内力与侧移的计算,这些计算都假定结构在楼面结构平面内刚度无限大(忽略楼面结构在平面的弯曲变形和剪切变形),并且均假定结构的侧移仅由平动产生。
这些计算是在水平荷载合力作用线通过结构抗侧刚度的中心时的计算。
当水平荷载合力作用线不通过结构的抗侧刚度中心时,结构在产生平移变形的同时还会产生扭转变形。
结构虽然平面形状对称,水平荷载合力通过平面形心,但抗侧力结构布臵不对称,结构会发生扭转。
工程中主要从设计方案,结构布臵,配筋、连接构造考虑,从而减少扭转和加强结构抗扭能力,来解决结构的扭转问题。
扭转的计算方法大致可以分为两类:一种是相对比较精确的空间分析方法,将结构视作空间结构,按3个方向的变形协调条件分析内力和位移。
另一种方法是简化近似分析,将结构看作若干榀平面结构的组合,考虑空间协调共同工作。
这种方法不能得到真正的扭转效应,只作为一种设计补充手段,但这种计算方法概念清楚,计算简便,可以手算。
对比较规则的结构可以得到相对较好的效果。
对不规则的结构而言,这种近似计算方法也能在一定程度上估计出扭转效应。
我们要学习的扭转计算只能作为一种近似计算,这种方法建立在荷载作用方向、平面结构及楼板在自身平面内刚度无限大这3个基本假定的基础上。
这种近似计算是先作平移变形条件下的内力分析,再考虑扭转作用时平移下的内力与位移计算结果进行修正,将修正结果作为考虑扭转作用效应下的内力和位移。
大连理工大学《高层建筑学》大作业学习中心: 姓 名: 学 号:题目二:底部剪力法。
钢筋混凝土5层框架经质量集中后计算简图如下图所示,各层高均为3m ,集中于各楼层的重力荷载代表值分别为:1500kN G =,2550kN G =,3580kN G =,4600kN G =,5450kN G =。
结构阻尼比0.05ξ=,自振周期为10.55s T =,Ⅰ1类场地类别,设计地震分组为第一组,抗震设防烈度为8度(设计基本地震加速度为0.30g )。
按底部剪力法计算结构在多遇地震时的水平地震作用及地震剪力。
3580kN=2550kN =1500kN=(a )计算简图4600kN=5450kN=解:查《建筑设计抗震规范》表5.2.1知,Tg=0.25s<T 1=0.55s<5Tg.表5.1.5,算得地震影响系数α1=(Tg/T 1)r η2αmax=(0.25/0.55)0.9×1.0×0.24=0.118总水平地震作用标准值:F Ek =α1Geq=0.118×(500+550+580+600+450)×85%=268.804kN因为T1=0.55s>1.4 Tg=1.4×0.25=0.35s,δn=0.08T+0.07=0.114各楼层水平地震作用标准值:Fi =GiHiFEk(1-δn)/∑GjHj(i=1,2,3…n)∑Gj Hj=500×3+550×6+580×9+450×15=23970kN·mF1k=[500×3×268.804×(1-0.114)]/23970=14.9kN F2k=[550×6×268.804×(1-0.114)]/23970=32.8kN F3k=[580×9×268.804×(1-0.114)]/23970=51.9kN F4k=[600×12×268.804×(1-0.114)]/23970=71.5kN F5k=[450×15×268.804×(1-0.114)]/23970=67.1kN 各楼层地震剪力为:V 1= F1k+ F2k+ F3k+ F4k+ F5k=238.2kNV 2= F2k+ F3k+ F4k+ F5k=223.3kNV 3= F3k+ F4k+ F5k=190.5kNV 4= F4k+ F5k=138.6 kN题目三:设计反应谱是通过什么样的结构计算模型得到的?阻尼比对反应谱有什么影响?钢筋混凝土结构及钢结构的阻尼比分别为多少?答:(1)设计反应谱是通过单自由度弹性体系的结构技术模型得到的。
一.高层建筑常见的结构体系?框架结构体系剪力墙结构体系框架-剪力墙结构体系筒体结构体系巨型结构体系二. 高层建筑结构布置原则?高层建筑结构应注重概念设计,重视结构的选型和平面、立面布置的规则性。
加强构造措施,择优选用抗震和抗风性能良好且经济合理的结构体系。
在抗震设计时,应保证结构的整体抗震性能,使整体结构具有必要的承载力、刚度和延性三基础有哪些类型及选型原则类型钢筋混凝土筏形基础箱型基础桩基选型原则1.当地基土质均匀、承载力高而沉降量小时,可以采用天然地基和竖向刚度较小的基础;反之,则应采用人工地基或竖向刚度较大的整体式基础2.当高层建筑基础直接搁置于未风华或微风化的岩层上,或者层数较少的独立裙房,可采用单独基础和条形基础;采用独立基础时应设置纵横向的拉梁3.当采用桩基时,应尽可能采用单根、单排大直径桩或扩底墩,使上部结构的荷载直接由柱或墙体传至桩顶,基础底板因此可以做得较薄四风荷载计算中各个系数含义和与之相关的影响系数影响系数:基本风压值w0:基本风压值w0系以当地比较空旷平坦地面上离地10m高统计所得的50年一遇10min平均最大风速v为标准,按w=1/2PV2确定的风压值风载体型系数:与建筑物平面外形、高宽比、风向与受风墙面所形成的角度有关,而且还与建筑物的立面处理、周围建筑物密集程度及其高低有关风压高度变化系数:地面粗糙度和高度,位于山区的高层建筑,还应考虑地形修正风振系数五剪力墙结构特点,布置以及按受力不同进行分类?剪力墙结构特点:钢筋混凝土剪力墙是截面高度较大而厚度型相对较小的“片”状构件,具有平面内承载力和刚度大的优点,但也具有剪切变化相对较大。
平面外较薄弱等不立性能。
剪力墙主要承受压、拉、弯、剪作用,在这些力作用下,剪力墙的破坏形态可分为弯曲破坏、弯剪破坏,剪切破坏和滑移破坏。
弯曲破坏分为大偏压和小偏压破坏。
大偏压破坏具有延性的破坏形态,而小偏压破坏的延性很小。
剪切破坏属于脆性破坏。
高层建筑结构辅导资料十一主 题:第四章 高层建筑结构近似算法(第3.4节) 学习时间:2014年6月9日--6月15日内 容:这周我们将学习第四章中的第3.4节,这部分主要介绍剪力墙结构在水平荷载作用下的内力与位移计算,下面整理出的框架供同学们学习,希望能够帮助大家更好的学习这部分知识。
一、学习要求1、掌握剪力墙结构在水平荷载作用下的内力与位移计算。
二、主要内容剪力墙结构在水平荷载作用下的内力与位移计算可按纵、横两个方向墙体分别按平面结构进行计算。
总水平荷载可以按各片剪力墙的等效刚度分配,然后进行单片剪力墙的计算。
max max 11()()()c eq ii m c eqjj E I q q E I+==∑ 11()()c eq ii m c eqjj E I F F E I+==∑ 式中:max q ——剪力墙承受倒三角形荷载时顶点的荷载;F ——剪力墙的顶点集中荷载;max ()i q ——第i 片剪力墙分配到的倒三角形荷载顶点的荷载; i F ——第i 片剪力墙分配到的顶点集中荷载; c E ,eq I ——分别为剪力墙的弹性模量及等效惯性矩。
(一)整体墙的内力与位移计算 1、应力计算当剪力墙孔洞面积与墙面面积之比不大于15%,且孔洞净距及孔洞至墙边距离大于孔洞边长时,可以作为整截面悬臂构件按平截面假定计算截面应力分布,如下图1所示。
My Iσ=VS Ibτ=式中:σ,τ,M 和V ——截面的正应力、剪应力、弯矩及剪力;I ,S ,b 和y ——截面惯性矩、静面矩,截面宽度及截面重心到所求正应力点的距离。
M V图1 整体墙内力分布2、顶点位移位移计算时,要考虑洞口对截面面积及刚度的削弱影响。
(1)小洞口整体墙的折算截面面积如下。
(1q A A =- 式中:A ——墙截面毛面积;OP A ——墙立面洞口面积; 0A ——墙立面总面积。
(2)等效惯性矩q I等效惯性矩取有洞口截面与无洞口截面的惯性矩按高度的加权平均值。
i i qiI h I h =∑∑(3)顶点位移墙高宽比H/h w ≤4时,除了弯曲变形,还应考虑剪切变形影响。
()()()3023023023.64111......60411............8311............3q q q q q q q q q EI V H EI H GA EI V H EI H GA EI V H EI H GA μμμ⎧⎛⎫+⎪ ⎪ ⎪⎪⎝⎭⎪⎛⎫⎪∆=+ ⎪⎨ ⎪⎪⎝⎭⎪⎛⎫⎪+ ⎪⎪ ⎪⎝⎭⎩倒三角形分布荷载均布荷载顶部集中荷载式中:0V ——底部截面剪力;G ——混凝土的剪切模量,取0.4c G E =μ——截面形状系数,矩形截面时=1.2μ;I 形截面取μ等于墙全截面面积除以腹板毛截面面积。
为了计算上的方便,引入等效刚度的概念,它把剪切变形与弯曲变形综合成弯曲变形的形式,上面各式可以写成如下形式:()()()30303011 (601)............81............3c eq c eq c eqV H E I V H E I V H E I ⎧⎪⎪⎪⎪∆=⎨⎪⎪⎪⎪⎩倒三角形分布荷载均布荷载顶部集中荷载 式中:eq I ——等效惯性矩,如果取0.4c G E =,则291qeq q q I I I A H μ=+(二)整体小开口墙的内力与位移计算 1、内力计算整体小开口墙墙肢截面的正应力可以看作是由两部分弯曲应力组成的,其中一部分是作为整体悬臂墙作用产生的正应力,另一部分是作为独立悬臂墙产生的正应力。
局部弯矩不超过整体弯矩的15%,如下图2所示。
图2 小开口墙的受力情况整体小开口墙的内力可按下式计算。
墙肢弯矩 0.850.15j jj iijI I M M M II=+∑墙肢轴力 0.85j j j iA y N M I=墙肢剪力 2jj i j j jA I V V A I ⎛⎫=+⎪ ⎪⎝⎭∑∑ 式中:i M ,i V ——第i 层总弯矩和总剪力;j I ,j A ——第j 墙肢的截面惯性矩和截面面积; j y ——第j 墙肢截面形心至组合截面形心的距离;I ——组合截面惯性矩。
连梁的剪力可由上、下墙肢的轴力差计算。
剪力墙多数墙肢基本均匀,又符合整体小开口墙的条件,当有个别细小墙肢时,仍可按整体小开口墙计算内力,但小墙肢端部宜按下式计算,附加局部弯曲的影响如下式:0j j j M M M =+∆2j jh M V ∆= 式中:0j M ——按整体小开口墙计算的墙肢弯矩;j M ∆——由于小墙肢局部弯曲增加的弯矩; j V ——第j 墙肢剪力; 0h ——洞口高度。
2、顶点位移考虑到开孔后刚度的削弱,应将计算结果乘以 1.20。
因此整体小开口墙的顶点位移可以按下式计算。
()()()4max 2424211 3.641.21......6041.21...................831.21..................3q H EI EI GAH qH EI EI GAH PH EI EI GAH μμμ⎧⎛⎫⨯+ ⎪⎪⎝⎭⎪⎪⎪⎛⎫∆=⨯+⎨ ⎪⎝⎭⎪⎪⎛⎫⨯+⎪ ⎪⎪⎝⎭⎩倒三角形分布荷载均布荷载顶部集中荷载 式中:A ——截面总面积,1mj j A A ==∑I——剪力墙对组合截面形心的惯性矩,1211m mj j j j j I I A y +===+∑∑(三)联肢墙的内力与位移计算 1、连续化方法:把连梁看做分散在整个高度上的连续连杆。
如下图3所示。
0l a H0l a1I 2I 1A 2A图3 双肢墙及连梁连续化示意图2、基本假定:(1)忽略连梁轴向变形,即同一高度上各个墙肢的水平位移相同。
(2)各墙肢的变形曲线相似,即各墙肢在同一高度上,截面转角和曲率相等,因此连梁的两端转角相等,连梁的反弯点在跨中,连梁的作用可以沿高度均匀分布的连续弹性薄片代替。
(3)各墙肢截面、连梁截面、层高等几何参数沿高度均不变。
3、内力求解以等肢双肢剪力墙为例,如下图4所示。
()x δ()x τ()x τ图4 双肢墙的基本体系将连续化后的连系梁沿中线切开,由于跨中为反弯点,故切开后截面上只有集度()x τ及轴力集度()x δ。
沿连梁切口处未知力()x τ方向上各因素将使其产生相对位移,但总的相对位移为零。
连梁轴力不引起连梁竖向相对位移,不改变整体截面的总弯矩。
墙肢剪切变形不引起连梁竖向相对位移。
墙肢弯曲变形、墙肢轴向变形以及连梁弯曲变形和剪切变形引起连梁中点切口处竖向相对位移,如下图5所示。
3δ2δ1δ(a)连梁弯曲和剪切变形(b)墙肢轴向变形(c)墙肢弯曲变形1θ2θ12mθθθ==图5 连梁中点的相对位移由于连梁中点处总的相对位移为零,则有:123()()()0x x x δδδ++=式中:1()x δ——墙肢弯曲变形产生的相对位移;2()x δ——墙肢轴向变形产生的相对位移; 3()x δ——连梁弯曲或剪切变形产生的相对位移。
将各种变形产生的δ代入上式,经整理可得:()()()()2123121200032312120312031212''()()24121......()()121......................................()12.......b b b b b I A A a x x hl I I A A I a EI l V x V I I hl H G A A H hl I a x V I I hl HI a V I I hlττμ⎡⎤+-+⎢⎥+⎣⎦⎛⎫⋅-- ⎪++⎝⎭⎛⎫=⋅- ⎪+⎝⎭-⋅+倒三角形荷载均布荷载..........................................()⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩顶部集中荷载 式中:0V ——基底总剪力;b I ——计及剪切变形影响后的连梁折算惯性矩;000022123011b b b b b b b I I I EI I GA l A l μμ=≈++l ——连梁的计算跨度,02bh l l =+; μ——截面上剪力分布的不均匀系数,对矩形截面, 1.2μ=; 解微分方程,可以求得()x τ,()x τ求得后可得双肢墙的内力。
连梁对墙肢的约束弯矩为()()m x x a τ=⋅j 层连梁的剪力为:()bj j V x h τ=⋅ j 层连梁的端弯矩为:02bj bj l M V =⋅j 层墙肢的轴力为:...(1,2)nij bk k jN V i ===∑j 层墙肢的弯矩为:11122212()j j n j pj k k j I M M I I I M M I I M M m x =⎧=⎪+⎪⎪⎪=⎨+⎪⎪=-⎪⎪⎩∑4、联肢墙顶点位移30303011......()601........()81........()3c eq c eq c eqV H E I V H E I V H E I ⎧⋅⎪⎪⎪⎪∆=⋅⎨⎪⎪⎪⋅⎪⎩倒三角形荷载均布荷载顶部集中荷载 式中c eq E I 为双肢墙的等效刚度,三种荷载下分别按下式计算。
2221 3.641413c ic i c eq c i E I T T E I E I T T E I T T αααγψγψγψ⎧⎪+-+⎪⎪⎪=⎨+-+⎪⎪⎪+-+⎪⎩∑∑∑ 232222260122sh 2sh +113ch ch ch 8112sh +2ch ch 3sh 1ch αααααααααααψαααααααααα⎧⎛⎫-- ⎪⎪⎝⎭⎪⎪⎛⎫=--⎨ ⎪⎝⎭⎪⎪⎛⎫-⎪ ⎪⎝⎭⎩22=ii iE I H G A γμ∑∑5、双肢墙位移及内力分布规律,如下图6所示。
HHOH α值较小α值较大图6 双肢墙变形与内力沿高度变化图(1)侧移曲线呈弯曲型,连梁与墙的刚度比α越大,墙的抗侧刚度越大。
(2)连梁的最大剪力不在底层,随着连梁与墙刚度比α的增大,连梁的剪力加大,剪力最大的梁在高度上的位置下移。
(3)墙肢轴力等于该截面以上所有连梁剪力之和,当连梁与墙的刚度比α增大时,连梁剪力加大,墙肢轴力也加大。
(4)连梁与墙的刚度比α增大时,墙肢弯矩则减小,轴力必然增大。
(四)壁式框架的内力与位移计算 1、计算简图当连梁刚度较大时,当连梁刚度接近于或者大于墙肢刚度的时候,其性能接近于框架,大部分层墙肢具有反弯点,可以按带刚域框架进行内力位移计算,这种框架具有宽梁宽柱的特点,也可以把连梁、墙肢简化成带刚域的变截面杆件,假定刚域部分没有转角,成为带刚域框架或称为壁式框架。
1c l 2c l 1b l 2b l cb ch 1c 2c 1a 2a 刚域图7 壁式框架计算简图上图7中的刚域是指壁梁、柱截面相交区(非结点),认为不产生变形的刚性区域。