第三章37概率

第三章 随机变量与分布函数1、直线上有一质点，每经一个单位时间，它分别以概率p 或p -1向右或向左移动一格，若该质点在时刻0从原点出发，而且每次移动是相互独立的，试用随机变量来描述这质点的运动（以n S 表示时间n 时质点的位置）。

2、设ξ为贝努里试验中第一个游程（连续的成功或失败）的长，试求ξ的概率分布。

3、c 应取何值才能使下列函数成为概率分布：（1）;,,2,1,)(N k Nck f Λ==（2）,,2,1,!)(Λ==k k c k f k λ 0>λ。

4、证明函数)(21)(||∞<<-∞=-x e x f x 是一个密度函数。

5、若ξ的分布函数为N （10，4），求ξ落在下列范围的概率：（1）（6，9）；（2）（7，12）；（3）（13，15）。

6、若ξ的分布函数为N （5，4），求a 使：（1）90.0}{=<a P ξ；（2）01.0}|5{|=>-a P ξ。

7、设}{)(x P x F ≤=ξ，试证)(x F 具有下列性质：（1）非降；（2）右连续；（3）,0)(=-∞F 1)(=+∞F 。

8、试证：若αξβξ-≥≥-≥≤1}{,1}{12x P x P ，则)(1}{21βαξ+-≥≤≤x x P 。

9、设随机变量ξ取值于[0，1]，若}{y x P <≤ξ只与长度x y -有关（对一切10≤≤≤y x ），试证ξ服从[0，1]均匀分布。

10、若存在Θ上的实值函数)(θQ 及)(θD 以及)(x T 及)(x S ，使)}()()()(ex p{)(x S D x T Q x f ++=θθθ，则称},{Θ∈θθf 是一个单参数的指数族。

证明（1）正态分布),(20σm N ，已知0m ，关于参数σ；（2）正态分布),(200σm N ，已知0σ，关于参数m ；（3）普阿松分布),(λk p 关于λ都是一个单参数的指数族。

但],0[θ上的均匀分布，关于θ不是一个单参数的指数族。

高中数学必修3 第三章 概率 知识点总结及强化训练一、 知识点总结3.1.1 —3.1.2随机事件的概率及概率的意义 1、基本概念：（1）必然事件：在条件S 下，一定会发生的事件，叫相对于条件S 的必然事件； （2）不可能事件：在条件S 下，一定不会发生的事件，叫相对于条件S 的不可能事件； （3）确定事件：必然事件和不可能事件统称为相对于条件S 的确定事件；（4）随机事件：在条件S 下可能发生也可能不发生的事件，叫相对于条件S 的随机事件；（5）频数与频率：在相同的条件S 下重复n 次试验，观察某一事件A 是否出现，称n 次试验中事件A出现的次数nA 为事件A 出现的频数；称事件A 出现的比例fn(A)=n n A为事件A 出现的概率：对于给定的随机事件A ，如果随着试验次数的增加，事件A 发生的频率fn(A)稳定在某个常数上，把这个常数记作P （A ），称为事件A 的概率。

（6）频率与概率的区别与联系：随机事件的频率，指此事件发生的次数nA 与试验总次数n 的比值n n A，它具有一定的稳定性，总在某个常数附近摆动，且随着试验次数的不断增多，这种摆动幅度越来越小。

我们把这个常数叫做随机事件的概率，概率从数量上反映了随机事件发生的可能性的大小。

频率在大量重复试验的前提下可以近似地作为这个事件的概率3.1.3 概率的基本性质 1、基本概念：（1）事件的包含、并事件、交事件、相等事件（2）若A ∩B 为不可能事件，即A ∩B=ф，那么称事件A 与事件B 互斥；（3）若A ∩B 为不可能事件，A ∪B 为必然事件，那么称事件A 与事件B 互为对立事件；（4）当事件A 与B 互斥时，满足加法公式：P(A ∪B)= P(A)+ P(B)；若事件A 与B 为对立事件，则A ∪B 为必然事件，所以P(A ∪B)= P(A)+ P(B)=1，于是有P(A)=1—P(B)2、概率的基本性质：1）必然事件概率为1，不可能事件概率为0，因此0≤P(A)≤1； 2）当事件A 与B 互斥时，满足加法公式：P(A ∪B)= P(A)+ P(B)；3）若事件A 与B 为对立事件，则A ∪B 为必然事件，所以P(A ∪B)= P(A)+ P(B)=1，于是有P(A)=1—P(B)；4）互斥事件与对立事件的区别与联系，互斥事件是指事件A 与事件B 在一次试验中不会同时发生，其具体包括三种不同的情形：（1）事件A 发生且事件B 不发生；（2）事件A 不发生且事件B 发生；（3）事件A 与事件B 同时不发生，而对立事件是指事件A 与事件B 有且仅有一个发生，其包括两种情形；（1）事件A 发生B 不发生；（2）事件B 发生事件A 不发生，对立事件互斥事件的特殊情形。

第三章 随机变量与分布函数1、直线上有一质点，每经一个单位时间，它分别以概率p 或p −1向右或向左移动一格，若该质点在时刻0从原点出发，而且每次移动是相互独立的，试用随机变量来描述这质点的运动（以n S 表示时间n 时质点的位置）。

2、设ξ为贝努里试验中第一个游程（连续的成功或失败）的长，试求ξ的概率分布。

3、c 应取何值才能使下列函数成为概率分布：（1）;,,2,1,)(N k N c k f L ==（2）,,2,1,!)(L ==k k c k f kλ 0>λ。

4、证明函数)(21)(||∞<<−∞=−x e x f x 是一个密度函数。

5、若ξ的分布函数为N （10，4），求ξ落在下列范围的概率：（1）（6，9）；（2）（7，12）；（3）（13，15）。

6、若ξ的分布函数为N （5，4），求a 使：（1）90.0}{=<a P ξ；（2）01.0}|5{|=>−a P ξ。

7、设}{)(x P x F ≤=ξ，试证)(x F 具有下列性质：（1）非降；（2）右连续；（3）,0)(=−∞F 1)(=+∞F 。

8、试证：若αξβξ−≥≥−≥≤1}{,1}{12x P x P ，则)(1}{21βαξ+−≥≤≤x x P 。

9、设随机变量ξ取值于[0，1]，若}{y x P <≤ξ只与长度x y −有关（对一切10≤≤≤y x ），试证ξ服从[0，1]均匀分布。

10、若存在Θ上的实值函数)(θQ 及)(θD 以及)(x T 及)(x S ，使)}()()()(exp{)(x S D x T Q x f ++=θθθ，则称},{Θ∈θθf 是一个单参数的指数族。

证明（1）正态分布),(20σm N ，已知0m ，关于参数σ；（2）正态分布),(200σm N ，已知0σ，关于参数m ；（3）普阿松分布),(λk p 关于λ都是一个单参数的指数族。

概率论与数理统计统计课后习题答案(有过程)第一章习题解答1．解：（1）Ω=｛0，1，…，10｝；（2）Ω=｛，1，…，100n｝，其中n为小班人数；n（3）Ω=｛√,×√, ××√, ×××√,…｝,其中√表示击中，×表示未击中；（4）Ω=｛（x,y）｝。

2．解：（1）事件AB表示该生是三年级男生，但不是运动员；（2）当全学院运动员都是三年级学生时，关系式是正确的；（3）全学院运动员都是三年级的男生，ABC=C成立；（4）当全学院女生都在三年级并且三年级学生都是女生时，=B成立。

3．解：（1）ABC；（2）AB；（3）；（4）；（5）；（6）4．解：因，则P（ABC）≤P（AB）可知P（ABC）=0 所以A、B、C至少有一个发生的概率为P（A∪B∪C）=P（A）+P（B）+P（C）-P（AB）-P（AC）-P（BC）+P（ABC）=3×1/4-1/8+0 =5/85．解：（1）P（A∪B）= P（A）+P（B）-P（AB）=0.3+0.8-0.2=0.9 P(A)=P（A）-P（AB）=0.3-0.2=0.1（2）因为P（A∪B）= P（A）+P（B）-P（AB）≤P（A）+P（B）=α+β, 所以最大值maxP （A∪B）=min(α+β,1)；又P（A）≤P（A∪B），P（B）≤P（A∪B）,故最小值min P（A∪B）=max(α,β)6．解：设A表示事件“最小号码为5”，B表示事件“最大号码为5”。

223由题设可知样本点总数，。

2C52C411所以；7．解：设A表示事件“甲、乙两人相邻”，若n个人随机排成一列，则样本点总数为n!，， 1若n个人随机排成一圈.可将甲任意固定在某个位置，再考虑乙的位置。

表示按逆时针方向乙在甲的第i个位置，。

则样本空间，事件所以8．解：设A表示事件“偶遇一辆小汽车，其牌照号码中有数8”，则其对立事件A表示“偶遇一辆小汽车，其牌照号码中没有数8”，即号码中每一位都可从除8以外的其他9个数中取，因此A包含的基本事件数为，样本点总数为104。

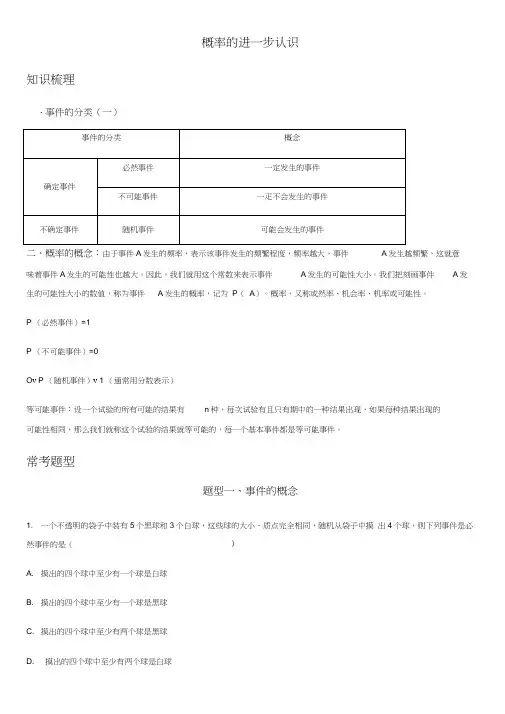
概率的进一步认识知识梳理、事件的分类（一）二、概率的概念：由于事件A发生的频率，表示该事件发生的频繁程度，频率越大，事件A发生越频繁，这就意味着事件A发生的可能性也越大。

因此，我们就用这个常数来表示事件A发生的可能性大小。

我们把刻画事件A发生的可能性大小的数值，称为事件A发生的概率，记为P（A）。

概率，又称或然率、机会率、机率或可能性。

P （必然事件）=1P （不可能事件）=0O v P （随机事件）v 1 （通常用分数表示）等可能事件：设一个试验的所有可能的结果有n种，每次试验有且只有期中的一种结果出现，如果每种结果出现的可能性相同，那么我们就称这个试验的结果就等可能的，每一个基本事件都是等可能事件。

常考题型题型一、事件的概念1. 一个不透明的袋子中装有5个黑球和3个白球，这些球的大小、质点完全相同，随机从袋子中摸出4个球，则下列事件是必然事件的是（）A. 摸出的四个球中至少有一个球是白球B. 摸出的四个球中至少有一个球是黑球C. 摸出的四个球中至少有两个球是黑球D. 摸出的四个球中至少有两个球是白球2. 从标号分别为1、2、3、4、5的5张卡片中，随机抽出1张。

下列事件中，必然事件是（A、标号小于6 B 、标号大于6C标号是奇数 D 、标号是33、把下列事件进行分类A. 如果|a|=|b| ，那么a=bB. 三角形的内角和是360 °C. 明天太阳从西边升起D. 篮球队员在罚球线上投篮一次，未投中E. 实心铁球投入水中会沉入水底F. 抛出一枚硬币，落地后正面朝上抛掷一枚硬币四次，有两次正面朝上G. 打开电视频道，正在播放《十二在线》H. 射击运动员射击一次，命中十环I. 方程x2-2x-仁0 必有实数根J. 单项式加上单项式，和为多项式K. 13名同学中至少有两名同学的出生月份相同L. 体育课上，小刚跑完1000米所用时间为1分钟M. 扇形统计图中，所有百分比的和为100%（1）必然事件：⑵不可能事件：____________________________________________随机事件：______________题型二、频率概率（1）一次概率问题1 •端午节吃粽子是中华民族的传统习俗，妈妈买了2只红豆粽、3只碱水粽、5只咸肉粽，粽子除内部馅料不同外1 11 1 A. 10 B.5C.3D.22•甲、乙、丙三人站成一排拍照，则甲站在中间的概率是（ ）111A. 6 B • 3 C • 23.下列说法正确的是（ ）B. 随机抛一枚硬币，落地后正面一定朝上C. 同时掷两枚均匀的骰子，朝上一面的点数和为 61D. 在一副没有大小王的扑克牌中任意抽一张，抽到的牌是 6的概率是134.在一个不透明的布袋中装有若干个只有颜色不同的小球，如果袋中有红球5个，黄球4个，其余为白球，从袋1子中随机摸出一个球，“摸出黄球”的概率为 2 3，则袋中白球的个数为（）A. 2 B . 3 C . 4 D . 125. 用2, 3, 4三个数字排成一个三位数，则排出的数是偶数的概率为 _______________6. 长度分别为3cm, 4cm, 5cm, 9cm 的四条线段，任取其 中三条能组成三角形的概率是（2）二次概率（用树状图求概率）1. 一个不透明的袋子中有三个完全相同的小球，把它们分别标号为1,2,3,随机摸出一个小球，记下标号后放回，再随机摸出一个小球并记下标号，两次摸出的小球标号的和是偶数的概率是（）2 在一个不透明的袋子中，有 2个白球和2个红球，它们只有颜色上的区别，从袋子中随机地摸出一个球记下颜色 放回，再随机地摸出一个球 ，则两次都摸到白球的概率为 。

概率论与数理统计实践考核37作业第⼀章随机事件与概率三、计算题1.设P (A )=0.4, P (B )=0.2, (|)0.3P B A =, 求P (AB )以及P (A |B ).解:由(|)0.3P B A =得:()0.3,()P AB P A =即()()0.31()P B P AB P A -=-, 解得:P (AB )=0.02. 从⽽, ()0.02(|)0.1()0.2P AB P A B P B ===.2.已知,()0.2,()0.3,A B P A P B ?==求：(1)(),()P A P B ；(2)P (AB )；(3)()P AB ；(4) ()P A B ；(5)P (B -A ).解：(1)由概率的性质，知()1()0.8,P A P A =-=()1()0.7P B P B =-=； (2)因为A B ?，所以AB A =，P (AB )=P (A )=0.2； (3)()P AB =P (A -AB )=P (A )-P (AB )=P (A )-P (A )=0； (4) 因为A B ?，所以A B B =, ()P A B =P (B )=0.3；或者，()P A B =P (A )+P(B )-P (AB )=0.2+0.3-0.2=0.3； (5) P (B -A )=P (B )-P (AB )=0.3-0.2=0.1.3.若事件A 与B 互不相容，P (A )=0.6, P (A+B )=0.9, 求：(1)()P AB ；(2)(|)P A B ；(3)()P AB .解:(1) 因A 与B 互不相容，故AB =Φ，P (AB )=0，所以()P AB =1-P (AB )=1；(2) 因A 与B 互不相容，由加法公式：P (A+B )=P (A )+P (B )，得P (B )=0.3，从⽽ (|)P A B =()()()0.661()0.77()P AB P A P AB P B P B -===-；(3) ()P AB =1()1()10.90.1P AB P A B -=-+=-=.4.已知事件A 与B 相互独⽴，且P (A )=0.4, P (A+B )=0.6, 求(1)P (B )；(2)()P AB ；(3)P (A|B ).解：(1)因为事件A 与B 相互独⽴，所以P (AB )=P (A )P (B )，()()()()()()()()P A B P A P B P AB P A P B P A P B +=+-=+- 0.6=0.4+P (B )-0.4P (B )，解得：P (B )=13；(2) 因为事件A 与B 相互独⽴，所以A 与B 也相互独⽴，故()P AB =4()()15P A P B =； (3) 因为事件A 与B 相互独⽴，所以P (A|B )=P (A )=0.4.四、应⽤题6.盒⼦中有8个红球和4个⽩球，每次从盒⼦中任取⼀球，不放回地抽取两次，试求：(1) 两次取出的都是红球的概率；(2)在第⼀次取出⽩球的条件下，第⼆次取出红球的概率；(3)第⼆次取到红球的概率.解：A 1“第⼀次取出的是红球”，A 2“第⼆次取出的是红球”，则 (1)由乘法公式得，两次取出的都是红球的概率为：121218714()()(|)121133P A A P A P A A ===； (2)在第⼀次取出⽩球的条件下，第⼆次取出红球的概率为：218(|)11P A A =； (3)由全概率公式得，第⼆次取到红球的概率为： 2121121()()(|)()(|)P A P A P A A P A P A A =+ 87482121112113 =+=. 第⼆章随机变量及其概率分布三、计算题1.设连续型随机变量X 的分布函数为20,0(),011,1x F x x x x=≤，求X 的概率密度函数.解：由分布函数与概率密度函数之间的关系()()F x f x '=知，当0当1x ≥或0x ≤时，()f x =0，所以，X 的概率密度为2,01()0,x x f x <2.设X 服从参数p =0.2的0-1分布，求X 的分布函数及P (X <0.5).解：X 的分布律为当0x <时，()()F x P X x =≤=0；当01x ≤<时，()()F x P X x =≤=(0)0.8P X ==；当1x ≥时，()()F x P X x =≤=(0)(1)0.80.21P X P X =+==+=.所以，X 的分布函数为0,0()0.8,011,1x F x x x=≤；⽽P (X <0.5)= P (X =0)=0.8.3.设随机变量X ~U (a , b )，求X 的密度函数与分布函数.解：X 的密度函数为1,()0,a xb f x b a ?<=-其它；分布函数()()x F x f t dt -∞=?，当x a <时，()()x F x f t dt -∞=?00xdt -∞==?；当a x b ≤<时，()()xF x f t dt -∞=?10a xax a dt dt b a b a-∞-=+=--??；当x b ≥时，()()xF x f t dt -∞=?1001abx ab dt dt dt b a-∞=++=-??.所以，X 的分布函数为0,(),1,x a x a F x a x b b ax b=≤4.设随机变量X ~N (3, 4)，求：(1)P (2P (|X|>2)；(4)P (X >3).解：(1)P (2(3)(2)()()22F F ---=Φ-Φ(0)(0.5)=Φ-Φ- (0)[1(0.5)]=Φ--Φ=0.1915；(2) P (-4(10)(4)()()22F F -----=Φ-Φ =(3.5)(3.5)2(3.5)1Φ-Φ-=Φ-=0.9996；(3) P (|X|>2)=1(||2)P X -≤=1(22)1[(2)(2)]P X F F --≤≤=--- =2323 1[()()]22----Φ-Φ=(0.5)(2.5)1Φ-Φ+=0.6977； (4)P (X >3)=1(3)P X -≤=33 1(3)1()1(0)2F --=-Φ=-Φ=0.5.5.已知随机变量X 的密度函数为2,01()0,kx x f x ?<<=??其它，求：(1)常数k ；(2)分布函数；(3)(10.5)P X -<<..解：(1)因为()1f x dx +∞-∞=?，所以123100|133k kkx dx x ===?，故k =3. 即随机变量X 的概率密度为23,01()0,x x f x ?<<=??其它；(2)当0x <时，()()xF x f t dt -∞=?=0，当01x ≤<时，()()x F x f t dt -∞=?=023003xdt t dt x -∞+=??，当1x ≥时，()()xF x f t dt -∞=?=01210301xdt t dt dt -∞++=.所以，随机变量X 的分布函数为30,0(),011,1x F x x x x=≤；(3)(10.5)P X -<<3(0.5)(1)0.500.125F F =--=-=；第三章多维随机变量及其概率分布三、计算题1.已知⼆维离散型随机变量(X , Y )的联合分布为：(1)确定常数C ；(2)求(X , Y )关于X ，Y 的边缘分布.解：(1)由概率分布的性质知，11111+++++=1464812C ，解得：C =18；(2)11113(0)46824P X ==++=，11111(1)481224P X ==++=，从⽽，(X , Y )关于X 的边缘分布为：111(0)442P Y ==+=，117(1)6824P Y ==+=，115(2)81224P Y ==+=，从⽽，(X, Y)关于Y的边缘分布为：2.已知⼆维离散型随机变量(X, Y)的联合分布为：求(X , Y )关于X ，Y 的边缘分布. 解：111(0)012126P X ==++=，，，，所以，(X , Y )关于X 的边缘分布为：，，，从⽽，(X , Y )关于Y 的边缘分布为：3.设⼆维离散型随机变量(X , Y )的等可能值为(0, 0), (0, 1), (1, 0), (1, 1).求： (1) (X , Y )的联合概率分布律； (2) (X , Y )关于X , Y 的边缘概率分布. 解：(1)由题设知：115(1)+04612P X ==+=111(3)0+1264P X ==+=111(5)012126P X ==++=11(1)01241212P Y ==+++=(2)006124P Y ==+++=1111P Y ==+++=所以，(X , Y )的联合概率分布为：(2) 与上⾯1，2题作法相同，可得(X , Y )关于X , Y 的边缘概率分布分别为：1(0,0)(0,1)(1,0)(1,1)4P X Y P X Y P X Y P X Y ============4.设⼆维随机变量(X , Y )只能取下列数组中的值：1(0,0),(1,1),(1,),(2,0)3--，且取这些值的概率依次为1115,,,631212.(1)写出(X , Y )的分布律；(2)求(X , Y )关于X ，Y 的边缘分布律.解：(1)由题设可得(X , Y )的分布律为：(2) ，，，所以，(X , Y )关于X 的边缘分布为：115(1)012312P X =-=++=1(0)6P X ==5(2)12P X ==，，，从⽽，(X , Y )关于Y 的边缘分布为：5.设⼆维随机变量(X , Y )的分布律为：试问：X 与Y 是否相互独⽴？为什么？157(0)061212P Y ==++=11()312P Y ==1.解：可求得(X , Y )关于X ，Y 的边缘概率分布分别为：因为所以，X 与Y 相互独⽴.第四章随机变量的数字特征三、计算题1.设随机变量X 的分布律为求：(1)EX ；(2)E (X 2)；(3)E (3X 3+5).解：(1)EX =； (2)E (X 2)=；(3)E (3X 3+5)=3E (X 3)+5，⽽E (X 3)=，所以，.(,)()(),1,2;1,2.P X i Y j P X i P Y j i j =======(2)0.400.320.30.2-?+?+?=-222(2)0.400.320.3 2.8-?+?+?=333(2)0.400.320.30.8-?+?+?=-33(35)3()53(0.8)5 2.6E X E X +=+=?-+=2.设随机变量X 的分布律为求：期望EX 与⽅差DX ..解：；， .3.设随机变量X 的概率密度为6(1),01()0,x x x f x -<解：；， . 10.220.530.3 2.1EX =?+?+?=2222()10.220.530.3 4.9E X =?+?+?=222()() 4.9(2.1)0.49DX E X EX =-=-=()EX xf x dx +∞-∞=?1234100316(1)(2)|22x x dx x x =-=-=?22()()E X x f x dx +∞-∞=?13451003636(1)()|2510x x dx x x =-=-=?22()()DX E X EX =-31110420=-=4.设随机变量X的概率密度为||1()0,||1x f x x <=≥?，求：期望EX 与⽅差DX ..解：；，=.5.设随机变量X 的概率密度为,01()2,120,x x f x x x ≤≤??=-<其它，求：期望EX 与⽅差DX .解：=； =， =.第五章⼤数定律及中⼼极限定理三、计算题()EX xf x dx +∞-∞=10-==?22()()E X x f x dx +∞-∞=22110122-===?22()()DX E X EX =-1()EX xf x dx +∞-∞=?12231232010111(2)|()|133x dx x x dx x x x +-=+-=??22()()E X x f x dx +∞-∞=?12324134201011217(2)|()|4346x dx x x dx x x x +-=+-=?22()()DX E X EX =-161.已知随机变量X 服从均匀分布U [0，1]，估计下列概率：(1){|0.5|P X -≥； (2) 13{}22P X -<<.解：因为X ~U [0，1]，所以.(1)由切⽐雪夫不等式，得；(2).2.设X i (i =1, 2, ...,50)是相互独⽴的随机变量，且都服从泊松分布P (0.03), 令1i i Z X ==∑，试⽤中⼼极限定理计算(3)P Z ≥.解：因为X i ~P (0.03), 故EX i =DX i =0.03，且,11,212EX DX =={|0.5|P X -≥21112143DX ≤==13{}22P X -<<11{11}{||1}22P X P X =-<-<=-<21111111212DX ≥-=-=5011.5i i EZ EX ===∑,由中⼼极限定理知：.所以 ==1-0.8888=0.1112.3.设P (A )=0.4，现在进⾏1000次独⽴重复试验，(1)估计事件A 发⽣的次数在300~500之间的概率；(2)求事件A 发⽣的次数在300~500之间的概率.解：设随机变量X 表⽰1000次试验中A 发⽣的次数，由题意知：X ~B (1000,0.4), EX =400, DX =240.(1)由切⽐雪夫不等式得， =0.976.(2)因为n =1000很⼤，所以不能直接⽤⼆项分布计算. 由中⼼极限定理知，.≈1.4.设P (A )=0.5，利⽤中⼼极限定理求在100次重复独⽴试验中A ⾄少发⽣60次的概率.5011.5i i DZ DX ===∑~(1.51.5)Z N 近似，(3)P Z≥1(3)1(3)1P Z F =-<=-≈-Φ1(1.22)-Φ2(300500)(|400|100)1100DXP X P X <<=-<≥-~(400,240)X N近似(300500)21P X <<≈Φ-Φ=Φ-解：X 表⽰在100次重复独⽴试验中A 发⽣的次数，则X ~B (100，0.5),EX =50，DX =25，由中⼼极限定理：.所求概率为=1-0.9772=0.0228. 5.设X ~U [-1，1], Y ~N (0，14)，且X 与Y 相互独⽴，估计概率P (-1. 第六章统计量及其抽样分布三、计算题 1.已知样本值如下：19.1, 20.0, 21.2, 18.8, 19.6, 20.5, 22.0, 21.6, 19.4, 20.3. 求样本均值x ，样本⽅差2s ，样本⼆阶中⼼矩2b .解：样本均值；样本⽅差； ~(50,25)X N近似(60)1(60)1P X P X ≥=-<≈-Φ14410,123EX DX ===14()0,E X Y EX EY +=+=7(),12D X Y DX DY +=+=2()75(11)(||1)1111212D X Y P X Y P X Y +-<+<=+<≥-=-=101120.2510i i x x ===∑102211() 1.165101i i s x x ==-=-∑样本⼆阶中⼼矩2.设总体2~(,)X N µσ，样本121,,...,,n n X X X X +来⾃总体X ，2,n n X S 表⽰12,,...,n X X X 的样本均值和样本⽅差..解：因为，，且与相互独⽴，所以. ⼜，由t 分布的定义知：t (n -1).102211() 1.048510i i b x x ==-=∑211~(,)n n i i X X N n nσµ==∑21~(,)n X N µσ+n X 1n X +211~(0, )n n n X X N n σ++-~(0,1)n N 222(1)~(1)nn S n χσ--~(1),t n -。

北师大版九年级上册第三章概率的进一步认识知识归纳及例题【学习目标】1.进一步认识频率与概率的关系，加深对概率的理解；2.会用列表和画树状图等方法计算简单事件发生的概率；3.能利用重复试验的频率估计随机事件的概率；4.学会运用概率知识解决简单的实际问题. 【知识点梳理】要点一、用树状图或表格求概率 1.树状图当一次试验要涉及3个或更多个因素时，为了不重不漏地列出所有可能的结果，通常采用树形图，也称树形图、树图.树形图是用树状图形的形式反映事件发生的各种情况出现的次数和方式，以及某一事件发生的可能的次数和方式，并求出概率的方法. 知识点诠释：(1)树形图法适用于各种情况出现的总次数不是很大时，求概率的问题；(2)在用树形图法求可能事件的概率时，应注意各种情况出现的可能性务必相同. 2.列表法当一次试验要涉及两个因素，并且可能出现的结果数目较多时，为不重不漏地列出所有可能的结果，通常采用列表法.列表法是用表格的形式反映事件发生的各种情况出现的次数和方式，以及某一事件发生的可能的次数和方式，并求出概率的方法. 知识点诠释：（1）列表法适用于各种情况出现的总次数不是很大时，求概率的问题； （2）列表法适用于涉及两步试验的随机事件发生的概率. 3.用列举法求概率的一般步骤（1）列举（列表、画树状图）事件所有可能出现的结果，并判断每个结果发生的可能性是否都相等； （2）如果都相等，再确定所有可能出现的结果的个数n 和其中出现所求事件A 的结果个数m ； （3）用公式计算所求事件A 的概率.即P （A ）=. 知识点二、用频率估计概率 1.频率与概率的定义频率：在相同条件下重复n 次试验，事件A 发生的次数m 与试验总次数n 的比值.概率：事件A 的频率接近与某个常数，这时就把这个常数叫做事件A 的概率，记作P （A ）. 2.频率与概率的关系事件的概率是一个确定的常数，而频率是不确定的，当试验次数较少时，频率的大小摇摆不定，当试验次数增大时，频率的大小波动变小，并逐渐稳定在概率附近.可见，概率是频率的稳定值，而频率是概率的近似值. 知识点诠释：（1）频率本身是随机的，在试验前不能确定，无法从根本上来刻画事件发生的可能性的大小，在大量nm nm重复试验的条件下可以近似地作为这个事件的概率；（2）频率和概率在试验中可以非常接近，但不一定相等；（3）概率是事件在大量重复试验中频率逐渐稳定到的值，即可以用大量重复试验中事件发生的频率去估计得到事件发生的概率，但二者不能简单地等同，两者存在一定的偏差是正常的，也是经常的. 3.利用频率估计概率当试验的可能结果不是有限个，或各种结果发生的可能性不相等时，一般用统计频率的方法来估计概率.知识点诠释：用试验去估计随机事件发生的概率应尽可能多地增加试验次数，当试验次数很大时，结果将较为精确.类型一、用树状图或表格求概率1.同时抛掷两枚均匀硬币，正面都同时向上的概率是（ ）A ．B ．C ．D ．【答案】B.【解析】可能性有（正，正），（正，反），（反，正），（反，反）4种，正面都同时向上的占1种，所以概率为. 【总结升华】利用树状图法列出所有的可能，看符合题意的占多少. 举一反三：【变式1】袋中装有一个红球和一个黄球，它们除了颜色外其余均相同，随机从中摸出一球，记录下颜色放回袋中，充分摇匀后，再随机从中摸出一球，两次都摸到黄球的概率是（ ） A ．B ．C ．D ．【答案】C.【变式2】随机地掷两次骰子，两次掷得的点数相同的概率是（ ）. A ．BC D【答案】 D.2. （2016•大庆）一个盒子装有除颜色外其它均相同的2个红球和3个白球，现从中任取2个球，则取到的是一个红球、一个白球的概率为（ ） A ．B ．C ．D ．【思路点拨】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与取到的是一个红球、一个白球的情况，再利用概率公式求解即可求得答案．13141234141312143413【答案】C.【解析】解：画树状图得：∵共有20种等可能的结果，取到的是一个红球、一个白球的有12种情况， ∴取到的是一个红球、一个白球的概率为：=．故选C ．【总结升华】此题考查了列表法或树状图法求概率．注意此题是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．举一反三：【变式1】从分别标有1到9数字的9张卡片中任意抽取一张，抽到所标数字是3的倍数的概率为（ ）A ．B ．C ．D ． 【答案】D.【变式2】如图是地板格的一部分，一只蟋蟀在该地板格上跳来跳去，如果它随意停留在某一个地方，则它停留在阴影部分的概率是_____.【答案】P （停在阴影部分）=. 类型二、频率与概率3.关于频率和概率的关系，下列说法正确的是（ ） A. 频率等于概率 B. 当试验次数很大时，频率稳定在概率附近 C. 当试验次数很大时，概率稳定在频率附近 D. 试验得到的频率与概率不可能相等【思路点拨】对于某个确定的事件来说，其发生的概率是固定不变的，而频率是随着试验次数的变化而变化的. 【答案】B.【解析】事件的概率是一个确定的常数，而频率是不确定的，当试验次数较少时，频率的大小摇摆不定，当试验次数增大时，频率的大小波动变小，并逐渐稳定在概率附近. 【总结升华】概率是频率的稳定值，而频率是概率的近似值.1918291323类型三、利用频率估计概率4. 某商场设立了一个可以自由转动的转盘(如图)，并规定：顾客购物10元以上能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品，下表是活动进行中的一组统计数据：(1)计算并完成表格：落在“铅笔”的频率(2)请估计，当很大时，频率将会接近多少？(3)转动该转盘一次，获得铅笔的概率约是多少？(4)在该转盘中，标有“铅笔”区域的扇形的圆心角大约是多少？(精确到 1°)【答案与解析】(1) 0.68、0.74、0.68、0.69、0.6825、0.701；(2) 0.70；(3) 由（1）的频率值可以得出P（获得铅笔）=0.70；(4) 0.70×360°=252°.【总结升华】(1)试验的次数越多，所得的频率越能反映概率的大小；(2)频数分布表、扇形图、条形图、直方图都能较好地反映频数、频率的分布情况，我们可以利用它们所提供的信息估计概率．5.（2015春•泰兴市期末）在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球，其中红球有4个，白球有10个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在20%．（1）试求出a的值；（2）从中任意摸出一个球，下列事件：①该球是红球；②该球是白球；③该球是蓝球．试估计这三个事件发生的可能性的大小，并将三个事件按发生的可能性从小到大的顺序排列（用序号表示事件）．【思路点拨】（1）根据频率估计概率，可得到摸到红球的概率为20%，然后利用概率公式计算a的值；（2）根据概率公式分别计算出摸出一个球是红球或白球或蓝球的概率，然后根据概率的大小判断这三个事件发生的可能性的大小．【答案与解析】解：（1）a=4÷20%=20；（2）在一个暗箱里放有20个除颜色外都完全相同的红、白、蓝三种球，其中红球有4个，白球有10个，蓝求有6个，所以从中任意摸出一个球，该球是红球的概率=20%；该球是白球的概率==50%；该球是蓝球的概率==30%，所以可能性从小到大排序为：①③②．【总结升华】用频率估计概率，强调“同样条件，大量试验”. 举一反三：【变式1】为了估计池塘里有多少条鱼，从池塘里捕捞了1000条鱼做上标记，然后放回池塘里，经过一段时间，等有标记的鱼完全混合于鱼群中以后，再捕捞200条，若其中有标记的鱼有10条，则估计池塘里有鱼______________条． 【答案】条 .【变式2】一只箱子里原有3个球，其中2个白球，1个红球，它们除颜色外均相同．（1）从箱子中任意摸出两个球，用树状图或列表法列举出所有可能并求两次摸出球的都是白球的概率． （2）若从箱子中任意摸出一个球是红球的概率为，则需要再加入几个红球？ 【答案】类型四、概率的简单应用6. 把一副扑克牌中的3张黑桃牌（它们的正面牌面数字分别是3、4、5）洗匀后正面朝下放在桌面上．（1）如果从中随机抽取一张牌，那么牌面数字是的概率是多少？（2）小王和小李玩摸牌游戏，游戏规则如下：先由小王随机抽出一张牌，记下牌面数字后放回，洗匀后正面朝下，再由小李随机抽出一张牌，记下牌面数字．当张牌面数字相同时，小王胜；当张牌面数字不相同时，小李胜．现请你利用树状图或列表法分析游戏规则对双方是否公平？并说明理由.【思路点拨】（1）问属于古典概型；（2）问可以采用列表法或树状图法列出所有的可能，计算小王和小李各自取胜的概率，再去做判断. 【答案与解析】（1）P （抽到牌面数字４）=；（2）游戏规则对双方不公平，理由如下：53一共有9种可能的结果，每种结果发生的可能性相等，∴P（牌面数字相同）=；P（牌面数字不相同）=，∴小李胜的概率要大，游戏不公平.【总结升华】列表法可以不重不漏地列出所有可能的结果.举一反三：【变式】（2015•漳州）在一只不透明的袋中，装着标有数字3，4，5，7的质地、大小均相同的小球，小明和小东同时从袋中随机各摸出1个球，并计算这两个球上的数字之和，当和小于9时小明获胜，反之小东获胜．（1）请用树状图或列表的方法，求小明获胜的概率；（2）这个游戏公平吗？请说明理由．【答案】解：（1）根据题意画图如下：∵从表中可以看出所有可能结果共有12种，其中数字之和小于9的有4种，∵P（小明获胜）==；（2）∵P（小明获胜）=，∵P（小东获胜）=1﹣=，∵这个游戏不公平．23。