下载文档原格式
第一章静力学【竞赛知识要点】重心共点力作用下物体的平衡物体平衡的种类力矩刚体的平衡流体静力学（静止流体中的压强）【内容讲解】一.物体的重心1.常见物体的重心：质量均匀分布的三角板的重心在其三条中线的交点；质量均匀分布的半径R的半球体的重心在其对称轴上距球心3R/8处；质量均匀分布的高为h的圆锥体的重心在其对称轴上距顶点为3h/4处。
2.重心：在xyz 三维坐标系中，将质量为m的物体划分为质点m1、m2、m3……m n.设重心坐标为（x0,y0，z0）,各质点坐标为（x1,y1,z1）,(x2,y2,z2)……(x n,y n,z n).那么：mx0=∑m i x i my0=∑m i y i mz0=∑m i z i【例题】1、（1）有一质量均匀分布、厚度均匀的直角三角板ABC，∠A=30°∠B=90°，该三角板水平放置，被A、B、C三点下方的三个支点支撑着，三角板静止时，A、B、C三点受的支持力各是N A、N B、N C，则三力的大小关系是.（2）半径为R的均匀球体，球心为O点，今在此球内挖去一半径为0.5R的小球，且小球恰与大球面内切，则挖去小球后的剩余部分的重心距O点距离为.2、如图所示，质量分布均匀、厚度均匀的梯形板ABCD，CD=2AB，求该梯形的重心位置。
3、在质量分布均匀、厚度均匀的等腰直角三角形ABC（角C为直角）上，切去一等腰三角形APB，如图所示。
如果剩余部分的重心恰在P点，试证明：△APB的腰长与底边长的比为5：4.4、（1）质量分别为m,2m,3m……nm的一系列小球（可视为质点），用长均为L的细绳相连，并用长也是L的细绳悬于天花板上，如图所示。
求总重心的位置5、如图所示，质量均匀分布的三根细杆围成三角形ABC，试用作图法作出其重心的位置。
6、如图所示，半径为R圆心角为θ的一段质量均匀分布的圆弧，求其重心位置。
7、论证质量均匀分布的三角形板的重心在三条中线的交点上8、求半径为R的厚薄均匀的半圆形薄板的重心9、均匀半球体的重心问题10、均匀圆锥体的重心11、如图所示，有一固定的半径为R 的光滑半球体，将一长度恰好等于R 21、质量为m 的均匀链条搭在球体上，其一端恰在球体的顶点上，并用水平拉力拉住链条使之静止，求拉力的大小。
第一章静力学基础学习目标：1.理解力、刚体、约束、约束力的概念和静力学公理。
2.掌握物体受力图分析。
静力学是研究物体在力系作用下平衡规律的科学，主要解决两类问题：一是将作用在物体上的力系进行简化，即用一个简单的力系等效地替换一个复杂的力系，这类问题称为“力系的简化（或力系的合成）问题”；二是建立物体在各种力系作用下的平衡条件，这类问题称为“力系的平衡问题”。
静力学是建筑力学的基础，在土木工程实际中有着广泛的应用。
它所研究的两类问题（力系的简化和力系的平衡），对于研究物体的受力和变形都有十分重要的意义。
力在物体平衡时所表现出来的基本性质，也同样表现于物体在一般运动的情形中。
在静力学中关于力的合成、分解与力系简化的研究结果，可以直接应用于动力学。
本章将阐述静力学中的一些基本概念、静力学公理、建筑工程上常见的典型约束力与约束反力，以及物体的受力分析。
第一节基本概念一、力力的概念是人们在生活和生产实践中，通过长期的观察、分析和总结而逐步形成的。
当人们推动小车时，由于手臂肌肉的紧张和收缩而感受到了力的作用。
这种作用不仅存在于人与物体之间，而且广泛地存在于物体与物体之间，例如机车牵引车辆加速前进或者制动时，机车与车辆之间、车辆与车辆之间都有力的作用。
大量事实表明，力是物体（指广义上的物体，其中包括人）之间的相互作用，离开了物体，力就不可能存在。
力虽然看不见摸不着，但它的作用效应完全可以直接观察，或用仪器测量出来。
实际上，人们正是从力的效应来认识力本身的。
1.力的定义力是物体之间相互的机械作用。
由于力的作用，物体的机械运动状态将发生改变，同时还引起物体产生变形。
前者称为力的运动效应（或外效应）；后者称为力的变形效应（或内效应）。
在本课程中，主要讨论力对物体的变形效应。
2.力的三要素实践表明，力对物体作用的效应，决定于力的大小、方向（包括方位和指向）和作用点，这三个因素称为力的三要素。
力的大小表示力对物体作用的强弱。
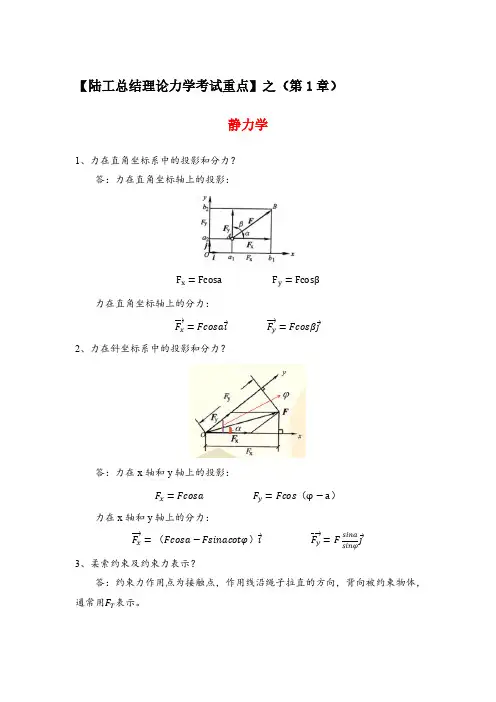
【陆工总结理论力学考试重点】之（第1章）静力学1、力在直角坐标系中的投影和分力？答：力在直角坐标轴上的投影：F x=Fcosa F y=Fcosβ力在直角坐标轴上的分力：F x⃗⃗⃗ =Fcosai F y⃗⃗⃗ =Fcosβj2、力在斜坐标系中的投影和分力？答：力在x轴和y轴上的投影：F x=Fcosa F y=Fcos（φ−a）力在x轴和y轴上的分力：jF x⃗⃗⃗ =（Fcosa−Fsinacotφ）i F y⃗⃗⃗ =F sinasinφ3、柔索约束及约束力表示？答：约束力作用点为接触点，作用线沿绳子拉直的方向，背向被约束物体，通常用F T表示。
4、光滑面约束及约束力表示？答：约束力作用点为接触点，方向总是沿接触面的公法线指向物体（即约束力总是垂直于公切线），通常用F N表示。
5、光滑中间铰链及约束力表示？答：约束力通常用两个正交分力F Ax、F Ay表示。
6、固定铰链支座及约束力表示？答：约束力通过销钉中心，通常用两个正交分力F Ax、F Ay表示。
7、活动铰链支座及约束力表示？答：约束力垂直于支撑面并通过铰链中心，通常用F N表示。
8、固定端约束及约束力表示？答：通常用两个正交分力F Ax、F Ay来限制物体的移动，用一个力偶M A（也称弯矩）来限制转动。
9、二力构件？答：在两个力作用下保持平衡的构件，称为二力构件。
二力构件可以是直杆，也可以是曲杆，如图中的AB、BC构件均为二力构件。
二力构件的特点：二力构件的二个作用力必通过两个端点的连线。
其AB、BC的受力图可表示为：二力构件的受力特点结论：两端是铰链连接，两端之间没有别的力作用的杆件，一定是二力构件；二力构件的二个作用力的作用线必通过两个作用点的连线。
10、平面汇交力系的简化？答：i 几何法（平行四边形法则）平行四边形法则求合力ii 解析法答：将平面汇交力系（F1、F2、⋯、F n）中的每个力向x轴和y轴投影，得到每个力在x轴和y轴上的分力F xi和F yi,则：合力在x轴上的投影：F Rx=∑F xi合力在y轴上的投影：F Ry=∑F yi 合力：F R=√F Rx2+F Ry211、力对点之矩？答：M o(F)=±Fh（单位：N∙m）点O称为矩心，距离h称为力臂（过O点做力F的作用线的垂线得到）。
