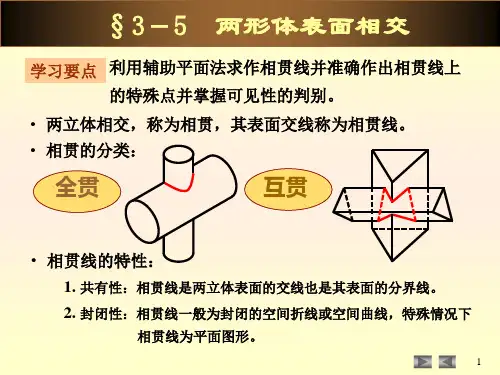
331 两立体相贯圆柱与平面体圆柱与圆柱相贯
- 格式:ppt
- 大小:2.42 MB
- 文档页数:13
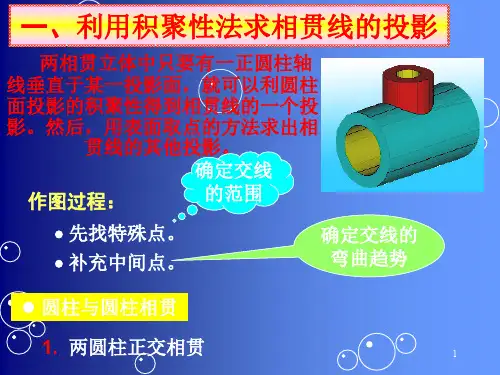


圆柱与圆柱相贯
1.表面取点法求作相贯线
两圆柱正交,且圆柱轴线为投影面垂直线时,在该投影面上,圆柱面投影是有积聚性的,相贯线在该投影面上的投影,就落在圆柱面有积聚性的投影上。
因此,可以在首先确定出相贯线的两面投影,在这些相贯线的已知投影上取一些点,再利用投影关系求作出相贯线的第三面投影上相应的点,这就是表面取点法。
例1:如图4-15所示,求作两正交圆柱的相贯线。
解:由图4-15b 可见,大、小圆柱的轴线分别垂直于侧立投影面和水平投影面,大圆柱的侧面投影积聚为圆,小圆柱的水平投影积聚为圆。
那么相贯线的侧面投影为圆弧(与大圆柱的部分积聚投影重合),相贯线的水平投影为圆(与小圆柱的水平积聚投影重合)。
相贯线的正面投影,可用已知点、线的两个投影求另外一个投影的方法来求得。
作图步骤如下(如图4-14c 所示):
a) 立体图 b) 原题 c) 作图步骤
图4-15 圆柱与圆柱正交 l )先求特殊点,即求相贯线上的最前、最后、最左、最右、最上、最下等点。
在水平投影的小圆周上直接确定出相贯线上最左、最右点的投影1、3和最前、最后点的投影2、4;对应在侧面投影中为1”、(3”)和2”、4”,也是相贯线上的最高、最低点的侧面投影;按投影关系可得出它们的正面投影1’、3’和2’、(4’)。
因为相贯两圆柱体前后对称,故最前、最后两点的正面投影重合。
2)求作一般位置点。
依连线光滑准确的需要,作出相贯线上若干个中间点的投影。
如在水平投影上取5、6点,其侧面投影为5”、6”,再求出其正面投影5’和6’。
3)依次光滑连接l’、5’、2’(4’)、6’、3’各点,即得相贯线的正面投影。