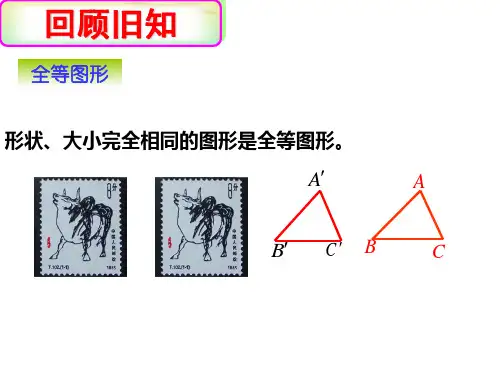
A1
B1
A
F1
C1
F
B C
E1
D1
E
D
问题1:在这两个多边形中,是否有对应相等的内角?
问题2:在这两个多边形中,夹相等内角的两边是否成比例?
形成认识:
对于四条线段a、b、c、
2.相似多边形的特征: 对应角相等,对应边的比相等. 符号语言(以四边形为例):
∵四边形ABCD∽四边形A′B′C′D′,
d,如果其中两条线段
• 改变k值的大小(如1∶3),再试一试.
• 通过上面的活动,你猜出了什么结 论?
AB 和 AC 都等于 AB AC 给定的值k (如 3 ).
2
判定三角形相似的方法
• 两边对应成比例且夹角相等的两个三角形相似.
A
B
A′
B′
C
C′
• 如图,在△ ABC与△A′B′C′中,如果
AB AC , 且∠A=∠A′,
2.若△ABC与△ A′B′C′ 相似,且AB:A′B′=1:2,
则△ABC与△ A′B′C′的相似比是
,
△ A′B′C′与△ABC的相似比是 2 .
当堂练习
1.观察下面的图形(a)~(g),其中哪些是与图形(1),(2)或(3) 相似的?
2.如图的两个四边形是否相似?
3.填空:
⑴如图1是两个相似的四边形, 则x= 2.5 ,y = 1.5 ,α= 90°;
的比(即它们长度的比)
与另两条线段的比相等,
如
a b
c d
(即ad=bc)
我们就说这四条线段是
AB BC CD DA AB BC CD DA
成比例线段,简称比例 线段.
A A, B B, C C, D D