1.2 锐角三角函数的计算

初中数学锐角三角函数初中知识点一、锐角三角函数的定义1.勾股定理：直角三角形两直角边a .b 的平方和等于斜边c 的平方。

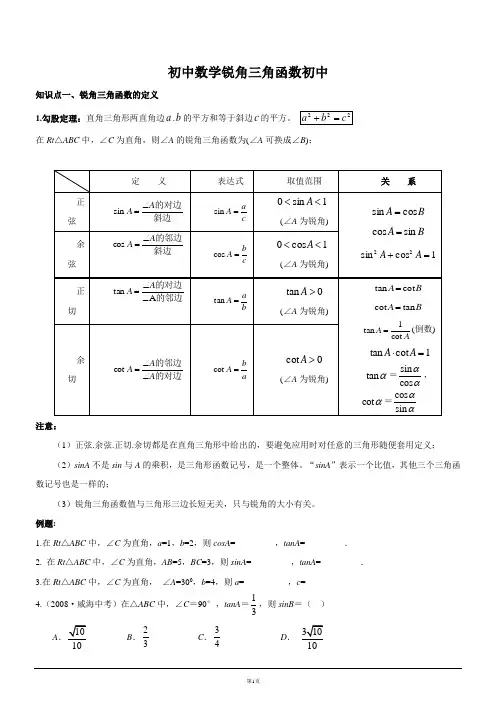
222c b a =+ 在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B )：定 义表达式 取值范围 关 系正弦 斜边的对边A A ∠=sin c aA =sin1sin 0<<A(∠A 为锐角)B A cos sin = B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=coscbA =cos1cos 0<<A(∠A 为锐角)正切的邻边的对边A tan ∠∠=A Aba A =tan 0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A Atan α＝sin cos αα，cot α＝cos sin αα余切的对边的邻边A A A ∠∠=cotab A =cot 0cot >A(∠A 为锐角)注意：（1）正弦.余弦.正切.余切都是在直角三角形中给出的，要避免应用时对任意的三角形随便套用定义；（2）sinA 不是sin 与A 的乘积，是三角形函数记号，是一个整体。

“sinA ”表示一个比值，其他三个三角函数记号也是一样的；（3）锐角三角函数值与三角形三边长短无关，只与锐角的大小有关。

例题:1.在Rt △ABC 中，∠C 为直角，a =1，b =2，则cosA =________ ，tanA =_________．2. 在Rt △ABC 中，∠C 为直角，AB =5，BC =3，则sinA =________ ，tanA =_________．3.在Rt △ABC 中，∠C 为直角， ∠A =300，b =4，则a =__________，c =__________4.（2008·威海中考）在△ABC 中，∠C ＝90°，tanA ＝31，则sinB ＝（ ） A ．1010B ．23 C ．34D ．310105.在△ABC 中，∠C =90°，a, b, c 分别为∠A ，∠B ，∠C 的对边，下列各式错误的是（ ）A .a =c ·sinAB ．b =c ·cosBC ．b =a ·tanBD ．a =b ·tanA6.在△ABC 中，∠C ＝90°，(1)已知：c ＝ 83，∠A ＝60°，求∠B .a .b ． (2) 已知：a ＝36， ∠A ＝30°，求∠B .b .c .7.（2009·漳州中考）三角形在方格纸中的位置如图所示，则tan 的值是（ ）A ．35B ．43 C ．34D ．45练习:1.在Rt △ABC 中，∠C 为直角，若sinA =53，则cosB =_________． 2.已知cosA =23，且∠B =900-∠A ，则sinB =__________． 3.∠A 为锐角，已知sinA =135，那么cos (900-A)=___________ ． 4.在Rt △ABC 中，∠C 为直角，AC =4，BC =3，则sinA =（ ） A ．43 B ．34 C ． 53 D ．54 5.在Rt △ABC 中，∠C 为直角，sinA =22，则cosB 的值是( ) A ．21 B ．23 C ．1D ．22知识点二、特殊角所对的三角函数值1. 0°.30°.45°.60°.90°特殊角的三角函数值(重要)三角函数0° 30°45°60°90° αsin0 2122 231 αcos1 23 22210 αtan 0 331 3- αcot-3133注意：记忆特殊角的三角函数值，可用下述方法：0°.30°.45°.60°.90°的正弦值分别是02.12.22.32.42，而它们的余弦值分别是42.32.22.12.02；30°.45°.60°的正切值分别是13.22.31，而它们的余切值分别是31.22.13。

2023合肥数学中考考点合肥数学中考考点1.解直角三角形1.1.锐角三角函数锐角a的正弦、余弦和正切统称∠a的三角函数。

如果∠a是Rt△ABC的一个锐角，则有1.2.锐角三角函数的计算1.3.解直角三角形在直角三角形中，由已知的一些边、角，求出另一些边、角的过程，叫做解直角三角形。

2.直线与圆的位置关系2.1.直线与圆的位置关系当直线与圆有两个公共点时，叫做直线与圆相交;当直线与圆有公共点时，叫做直线与圆相切，公共点叫做切点;当直线与圆没有公共点时，叫做直线与圆相离。

直线与圆的位置关系有以下定理：直线与圆相切的判定定理：经过半径的外端并且垂直这条半径的直线是圆的切线。

圆的切线性质：经过切点的半径垂直于圆的切线。

2.2.切线长定理从圆外一点作圆的切线，通常我们把圆外这一点到切点间的线段的长叫做切线长。

切线长定理：过圆外一点所作的圆的两条切线长相等。

2.3.三角形的内切圆与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形。

三角形的内心是三角形的三条角平分线的交点。

3.三视图与表面展开图3.1.投影物体在光线的照射下，在某个平面内形成的影子叫做投影。

光线叫做投影线，投影所在的平面叫做投影面。

由平行的投射线所形成的投射叫做平行投影。

可以把太阳光线、探照灯的光线看成平行光线，它们所形成的投影就是平行投影。

3.2.简单几何体的三视图物体在正投影面上的正投影叫做主视图，在水平投影面上的正投影叫做俯视图，在侧投影面上的正投影叫做左视图。

主视图、左视图和俯视图合称三视图。

产生主视图的投影线方向也叫做主视方向。

3.3.由三视图描述几何体三视图不仅反映了物体的形状，而且反映了各个方向的尺寸大小。

3.4.简单几何体的表面展开图将几何体沿着某些棱“剪开”，并使各个面连在一起，铺平所得到的平面图形称为几何体的表面展开图。

圆柱可以看做由一个矩形ABCD绕它的一条边BC旋转一周，其余各边所成的面围成的几何体。

浙教版数学九年级下册1.2《锐角三角函数的计算》说课稿2一. 教材分析《锐角三角函数的计算》是浙教版数学九年级下册第1章第2节的内容。

本节内容是在学生已经学习了锐角三角函数的定义和概念的基础上进行讲解的，主要让学生掌握锐角三角函数的计算方法，培养学生的运算能力和解决问题的能力。

教材通过例题和练习题的形式，使学生能够熟练运用锐角三角函数的计算方法解决实际问题。

二. 学情分析九年级的学生已经具备了一定的数学基础，对于锐角三角函数的定义和概念已经有了初步的了解。

但是，学生在计算方面可能还存在一些问题，如对计算过程的理解不够深入，运算速度和准确性有待提高。

因此，在教学过程中，需要注重引导学生理解计算方法，并通过练习题来提高学生的运算能力。

三. 说教学目标1.知识与技能目标：使学生掌握锐角三角函数的计算方法，能够熟练运用计算方法解决实际问题。

2.过程与方法目标：通过例题和练习题的讲解和练习，培养学生的运算能力和解决问题的能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的耐心和细心，使学生感受到数学在生活中的应用。

四. 说教学重难点1.教学重点：使学生掌握锐角三角函数的计算方法。

2.教学难点：对计算过程的理解和运用。

五. 说教学方法与手段1.教学方法：采用讲解法、例题解析法、练习法、小组合作学习法等。

2.教学手段：利用多媒体课件进行讲解和展示，使用黑板、粉笔进行板书。

六. 说教学过程1.导入：通过复习锐角三角函数的定义和概念，引导学生回顾已学的知识，为新课的学习做好铺垫。

2.讲解：讲解锐角三角函数的计算方法，通过例题进行解析，让学生理解计算过程和方法。

3.练习：布置练习题，让学生进行计算练习，巩固所学知识。

4.小组合作：学生分组进行讨论和合作，共同解决问题，培养学生的合作意识和解决问题的能力。

5.总结：对本节课的内容进行总结，强调计算方法和注意事项。

6.布置作业：布置适量的作业，让学生进行巩固练习。

锐角三角函数的计算（1）第一部分1．(1)用计算器求：sin20°= ；sin40°= ；sin60°= ；sin80°= ；由此，可用不等号连接：sin20°sin40°sin60°sin80°．(2)用计算器求：cos15°= ；cos35°= ；cos55°= ；cos75°= ．由此，可用不等号连接：cos15°cos35°cos55°cos75°．由此你能得到什么结论吗?2．用计算器求下列各式的值．（精确到)(1) sin15°18/+cos7°30/－tan54°42/；(2) sin48°25/+cos23°27/－tan48°•tan 81°52/.3．在△ABC中，∠C=90°，已知AB=10cm, =42°, 求△ABC的周长和面积.(精确到4．在某一时刻测得太阳光线与水平地面成44°角, 一棵竖起生长的松树在水平地面上的影子长为12m,则这棵松树的高度为(精确到.第二部分1. sin30°= ， cos45°= ， tan60°= ．2. 用计算器求：（1）sin18°= ；(2)cos36°= ；(3)tan63°= ．3. 用计算器比较大小：sin20° sin40°；cos55° cos75°．4.计算: °tan 40tan 50 = ．5. 与°°sin 34cos34的值相等的是（ ） A. sin68° B. cos68° C. tan68° D. tan34° 6.计算： sin25°+cos25°= ．(保留四个有效数字) 7. 用不等号连接右面的式子：cos40°_____cos20°．8. 若α为锐角，且sin α=35，则tan α等于 ．9.计算：(1) sin20°·cos20°(结果保留四个有效数字)；(2) sin 266°+cos 266°－tan27°·tan63°．10. 如图，小红从A 地向北偏东28°的方向走100米到B 地，再从B 地向正西走200米到C 地，求这时小红距A 地的距离.参考答案第一部分1．(1)0.3420,0.6428,0.8660,0.9848，<<<； （2）,,,,>>> 2．(1),(2); 3．,4．树高=12·tan44°≈ 第二部分1. sin30°= , cos45°= , tan60°= .答案：1222. 用计算器求：（1）sin18°= ；(2)cos36°= ；(3)tan63°= .答案：(1) (2) (3)3. 用计算器比较大小:：sin20° sin40°；cos55° cos75°.答案：< >4.计算： °tan 40tan 50 = .答案：15. 与°°sin 34cos34的值相等的是（ ）A. sin68°B. cos68°C. tan68°D. tan34° 答案：D6.计算： sin25°+cos25°= .(保留四个有效数字)答案：7. 用不等号连接右面的式子：cos40°_____cos20°.答案：<8. 若α为锐角，且sin α=35，则tan α等于 .答案：9.计算：(1) sin20°·cos20°(结果保留四个有效数字)；(2) sin266°+cos266°－tan27°·tan63°．答案：(1) (2) 010. 如图，小红从A地向北偏东28°的方向走100米到B地，再从B地向正西走200米到C地，求这时小红距A地的距离.解：∵AB=100m, ∠B=28°, ∴AD=AB·sin B=100sin28°,BD= AB·cos B=100cos28°. ∴CD=200－100cos28°.∴AC≈.。