计算机图形学边缘讲义填充算法

扫描线多边形填充算法扫描线多边形区域填充算法是按照扫描线顺序，计算扫描线与多边形的相交区间，再用要求的颜色显示这些去区间的像素（即完成填充）。

填充过程：1 求交：计算扫面线与多边形个边的交点。

2 排序: 把所有交点按x值地震顺序排序。

2 配对：两两配对，1,和2,3和4 等等。

每对交点代表扫面线与多边形的一个相交区间。

4 填充：把相交区间内的像素设置成多边形颜色。

相交顶点的数目确定：检查相交顶点的两条边的另外两个定点的y值。

按这两个y值中大于交点y值得个数是0,1,2来决定是取0,1或2个。

边界像素取舍：对扫描线与多边形的相交区间取左闭右开。

水平边界处理：水平边不参与求交计算，跳过。

相交：把多边形的所有边放在一个表中，处理每条扫描线是，按顺序从表中取出所有边，分别与扫面线求交。

改进：效率低，可只求与它相交的多边形的边进行求交运算。

算法思想及实现：活性边：与当前扫描线相交的边。

活性边表：把活性边按与扫描线线交点x坐标递增的顺序存放在一个链表中。

活性边的每个节点的内容：X ，X的变化量，Y的最大值，一个指针。

1 存放当前扫描线与边的交点坐标x值。

2 存放从当前扫描线到下一条扫描线间x的增量3 存放该边所交的最高扫面线号ymax;4 存放指向下一条边的指针。

算法的主要步骤：建立NET(new edge list)从最低扫面线开始到最高扫面线循环。

建立或调整AET(active edge list)按照AET总的接点顺序填充。

算法描述：算法描述：void polyfill (多边形polygon, 颜色color){for (各条扫描线i ){ 初始化新边表头指针NET [i]；把ymin = i 的边放进边表NET [i];}y = 最低扫描线号；初始化活性边表AET为空；for (各条扫描线i ){ 把新边表NET[i]中的边结点用插入排序法插入AET表，使之按x坐标递增顺序排列；遍历AET表，把配对交点区间(左闭右开)上的象素(x,y)，用drawpixel (x, y, color) 改写象素颜色值；遍历AET表，把y max= i +1的结点从AET表中删除，并把y max > i+1结点的x值递增D x；若允许多边形的边自相交，则用冒泡排序法对AET表重新排序；}} /* polyfill */。

68图3-26 各条扫描线的活性边表例如，扫描线0.5的y桶为空，则该扫描线对应的活性边表为空。

而扫描线1.5的y桶不为空，则将扫描线1.5的y桶指向的新边表插入到扫描线1.5对应的活性边表中。

在建立扫描线2.5的y桶时，首先检查是否有旧边删除，由于y = 2.5，大于扫描线1.5的活性边表中的y max，所以将边P1P2的结点信息从扫描线2.5的活性边表中删除；然后对未删除的P2P3边结点信息进行更新，即按照x = x + ∆x更新其中的x值；最后检查是否有新边插入，由于扫描线2.5的y桶不为空，所以将扫描线2.5的y桶指向的新边表中的结点信息按x值由小到大的顺序插入到扫描线2.5的活性边表中。

依此类推，当处理完所有的扫描线并建立相应的活性边表后，对每一条扫描线，依次从活性边表中成对地取出交点，并激活相应的像素。

其填充结果如图3-24所示。

3.4.4 边填充算法有序边表算法是一个有效的多边形填充算法，它将扫描转换过程中的计算种类减少，将求交计算方法简化，而且由于对每个显示的像素只访问一次，因此对于帧缓存输入输出的要求可降低为最小。

此外，由于算法与输入输出的具体操作无关，因此算法与设备也无关。

算法的主要缺点是数据结构复杂，表的维护和排序的开销较大，不适合硬件实现。

本小节要介绍的边填充算法无需复杂的链表结构，并且特别适合于有帧缓冲存储器的显示器。

1．简单的边填充算法边填充算法的基本思想是，对每一条与多边形相交的中心扫描线，将像素中心位于交点右方的全部像素取补（即异或写）。

屏幕像素的异或写操作的特点就是，第一次异或写操作，像素被置成前景色，第二次异或写操作，像素恢复为背景色。

算法的具体描述为：对于每一条与多边形相交的扫描线，计算中心扫描线与边的交点，设其交点为(x1, y1)，将像素中心位于(x1, y1)右方即满足x+0.5＞x1的全部像素取补（相当于异或写操作）。

对多边形的每一条边分别应用上述算法，处理的顺序可以是任意的，当所有的边都处理完以后，即可得到填充后的多边形。

计算机图形学——区域填充算法（基本光栅图形算法）⼀、区域填充概念区域：指已经表⽰成点阵形式的填充图形，是象素的集合。

区域填充：将区域内的⼀点（常称【种⼦点】）赋予给定颜⾊，然后将这种颜⾊扩展到整个区域内的过程。

区域填充算法要求区域是连通的，因为只有在连通区域中，才可能将种⼦点的颜⾊扩展到区域内的其它点。

1、区域有两种表⽰形式1）内点表⽰：枚举出区域内部的所有象素，内部所有象素着同⼀个颜⾊，边界像素着与内部象素不同的颜⾊。

2）边界表⽰：枚举出区域外部的所有象素，边界上的所有象素着同⼀个颜⾊，内部像素着与边界象素不同的颜⾊。

21）四向连通区域：从区域上⼀点出发可通过【上、下、左、右】四个⽅向移动的组合，在不越出区域的前提下，到达区域内的任意象素。

2）⼋向连通区域：从区域上⼀点出发可通过【上、下、左、右、左上、右上、左下、右下】⼋个⽅向移动的组合，在不越出区域的前提下，到达区域内的任意象素。

⼆、简单种⼦填充算法给定区域G⼀种⼦点（x, y）,⾸先判断该点是否是区域内的⼀点，如果是，则将该点填充为新的颜⾊，然后将该点周围的四个点（四连通）或⼋个点（⼋连通）作为新的种⼦点进⾏同样的处理，通过这种扩散完成对整个区域的填充。

这⾥给出⼀个四连通的种⼦填充算法（区域填充递归算法），使⽤【栈结构】来实现原理算法原理如下：种⼦像素⼊栈，当【栈⾮空】时重复如下三步：这⾥给出⼋连通的种⼦填充算法的代码：void flood_fill_8(int[] pixels, int x, int y, int old_color, int new_color){if(x<w&&x>0&&y<h&&y>0){if (pixels[y*w+x]==old_color){pixels[y*w+x]== new_color);flood_fill_8(pixels, x,y+1,old_color,new_color);flood_fill_8(pixels, x,y-1,old_color,new_color);flood_fill_8(pixels, x-1,y,old_color,new_color);flood_fill_8(pixels, x+1,y,old_color,new_color);flood_fill_8(pixels, x+1,y+1,old_color,new_color);flood_fill_8(pixels, x+1,y-1,old_color,new_color);flood_fill_8(pixels, x-1,y+1,old_color,new_color);flood_fill_8(pixels, x-1,y-1,old_color,new_color);}}}简单种⼦填充算法的不⾜a)有些像素会多次⼊栈，降低算法效率，栈结构占空间b)递归执⾏，算法简单，但效率不⾼，区域内每⼀像素都要进/出栈，费时费内存c)改进算法，减少递归次数，提⾼效率三、扫描线种⼦填充算法基本思想从给定的种⼦点开始，填充当前扫描线上种⼦点所在的⼀区段，然后确定与这⼀段相邻的上下两条扫描线上位于区域内的区段（需要填充的区间），从这些区间上各取⼀个种⼦点依次把它们存起来，作为下次填充的种⼦点。

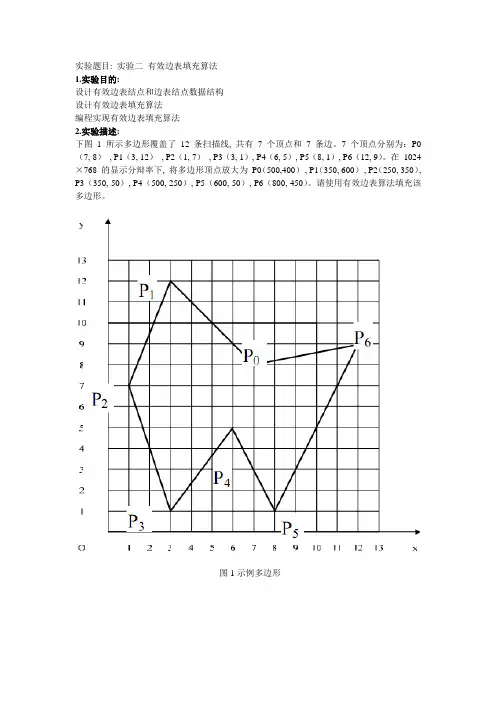
实验题目: 实验二有效边表填充算法1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图 1 所示多边形覆盖了12 条扫描线, 共有7 个顶点和7 条边。

7 个顶点分别为：P0（7, 8）, P1（3, 12）, P2（1, 7）, P3（3, 1）, P4（6, 5）, P5（8, 1）, P6（12, 9）。

在1024×768 的显示分辩率下, 将多边形顶点放大为P0（500,400）, P1（350, 600）, P2（250, 350）, P3（350, 50）, P4（500, 250）, P5（600, 50）, P6（800, 450）。

请使用有效边表算法填充该多边形。

图1示例多边形图2 屏幕显示多边形3.算法设计:（1）建立AET和BUCKET类；（2）初始化桶, 并在建立桶结点时为其表示的扫描线初始化为带头结点的链表；（3）对每个桶结点进行循环, 将桶内每个结点的边表合并为有效边表, 并进行有效边表循环；（4）按照扫描线从小到大的移动顺序, 计算当前扫描线与多边形各边的交点, 然后把这些交点按X值递增的顺序进行排序, 配对, 以确定填充区间；（5）用指定颜色点亮填充区间内的所有像素, 即完成填充工作。

4.源程序:1)//AET.hclass AET{public:AET();virtual ~AET();double x;int yMax;double k;//代替1/kAET *next;};//AET..cppAET::AET(){}AET::~AET(){}2) //Bucket.h#include "AET.h"class Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;};// Bucket.cppBucket::Bucket(){}Bucket::~Bucket(){}3)//TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数, 顶点存放在整型二维数组Point[N]中class CTestView : public CView{。

任课教师：李陶深教授tshli@12直线生成算法圆与椭圆的绘制算法5图元的概念436区域填充算法裁剪反走样技术4.4 区域填充算法4.4 区域填充算法—基础知识（3）线框多边形物体:只需扫描转换线段填充多边形物体:要扫描转换多边形本质：点阵表示。

特点：面着色，画面明暗自然、色彩丰富。

4.4 区域填充算法4.4 区域填充算法—基础知识（4）图形学中多边形的两种表示方式顶点表示：用多边形的有序顶点序列表示多边形点阵表示：用位于多边形内部的像素集合来表示多边形4.4 区域填充算法多边形边界的矢量形式数据之上，可用于程序填色，也可用于交互填色。

形边界的图像形式数据之上，并还需提供多边形边界内一点的坐标。

概括地说，该算法先画边界，然后对内定义区域填充。

所以，它一般只能用于人机交互填色，而难以用于程序填色。

4.4 区域填充算法—多边形填色算法的问题多边形填色算法面临的一个首要问题，是判断一个像素是在多边形内还是多边形外。

Question1: How to Judge…?Question2: How to improve …?图4.14 射线法图4.15 转角法4.4 区域填充算法4.4 区域填充算法4.4 区域填充算法4.4 区域填充算法4.4 区域填充算法大量的求交、乘除运算4.4 区域填充算法—扫描线填色算法（1）基本思路：扫描线算法按扫描线的顺序计算出扫描线与多边形的相交区间，然后用要求的颜色填充这些区间内的像素。

该算法利用了扫描线的连续性和边的连续性，避免对像素的逐点判断和反复求交运算，减少了计算量，提高了算法速度。

具体处理过程：先求出扫描线与多边形边的交点，利用扫描线的连续性求出多边形与扫描线相交的连续区域，然后利用多边形边的连续性，求出下一条扫描线与多边形的交点，对所有扫描线由上到下依次处理。

4.4 区域填充算法—扫描线填色算法（2） 算法实现的步骤：对每一条扫描线执行如下四步:(1) 求交：求扫描线与多边形各边的交点;(2) 排序：将求得的交点按递增顺序进行排序;(3) 交点配对：确定相交区间;(4) 区间填色：将相交区间内的像素置成多边形色, 相交区间外的像素置成背景色。

计算机图形学多边形填充算法计算机图形学中的多边形填充算法是指将给定的多边形区域进行颜色填充，以使其完全填充的过程。

在图形学中，多边形是由一系列连续的线段组成的封闭图形。

填充算法可用于渲染图形、绘制图像等应用场景。

多边形填充算法的目标是根据设计要求和用户输入，给定一个多边形的边界，将多边形的内部区域进行颜色填充。

填充算法的实现涉及到图像的扫描线和区域判定，以确定填充的区域和颜色。

在本文中，我们将介绍常见的多边形填充算法，包括扫描线填充算法、边界填充算法等，并讨论它们的优缺点和适用场景。

扫描线填充算法扫描线填充算法是一种常见且简单的多边形填充算法。

该算法将多边形划分为一条条水平扫描线，并通过判断扫描线与多边形边界的交点，确定填充区域。

具体步骤如下：1.找到多边形边界的最上端和最下端。

2.从最上端开始，逐行进行扫描。

3.在每一行，通过求解扫描线与多边形边界的交点，确定填充区域。

4.对于每个填充区域，根据设计要求进行颜色填充。

扫描线填充算法的优点是简单易懂、实现较为容易。

然而，该算法存在一些缺点。

首先，对于具有复杂形状的多边形，扫描线填充算法可能会产生很多不必要的计算，导致效率降低。

其次，该算法需要处理多边形边界相交的情况，可能出现像素重复填充的问题，需要进行额外的处理。

边界填充算法边界填充算法是另一种常见的多边形填充算法。

与扫描线填充算法不同的是，边界填充算法是从多边形的边界出发，向内部填充颜色。

该算法的基本思想是对多边形的每条边进行填充，最终得到多边形的填充区域。

具体步骤如下：1.遍历多边形的每条边，保存每条边的起点和终点。

2.对于每个边，根据设计要求进行颜色填充。

3.对于多边形内部的区域，根据边界的颜色填充。

边界填充算法的优点是适用于复杂形状的多边形，无需处理边界相交的问题。

然而，该算法的实现相对复杂，需要处理边界的细化以及边缘像素重复填充的问题。

适用场景不同的多边形填充算法在不同场景下有不同的适用性。

《计算机图形学》有序边表填充算法实验报告一、实验目的1、掌握有序边表算法填充多边形区域；2、理解多边形填充算法的意义；3、增强C语言编程能力。

二、算法原理介绍根据多边形内部点的连续性知：一条扫描线与多边形的交点中，入点和出点之间所有点都是多边形的内部点。

所以，对所有的扫描线填充入点到出点之间所有的点就可填充多边形。

判断扫描线上的点是否在多边形之内，对于一条扫描线，多边形的扫描转换过程可以分为四个步骤：（1）求交：计算扫描线与多边形各边的交点；（2）排序：把所有交点按x值递增顺序排序；（3）配对：第一个与第二个，第三个与第四个等等；每对交点代表扫描线与多边形的一个相交区间;（4）着色：把相交区间内的象素置成多边形颜色，把相交区间外的象素置成背景色。

p1,p3,p4,p5属于局部极值点，要把他们两次存入交点表中。

如扫描线y=7上的交点中，有交点(2,7,13)，按常规方法填充不正确，而要把顶点(7,7)两次存入交点表中(2,7,7,13)。

p2，p6为非极值点，则不用如上处理。

为了提高效率，在处理一条扫描线时，仅对与它相交的多边形的边进行求交运算。

把与当前扫描线相交的边称为活性边，并把它们按与扫描线交点x坐标递增的顺序存放在一个链表中，称此链表为活性边表(AET)。

对每一条扫描线都建立一个与它相交的多边形的活性边表（AET）。

每个AET的一个节点代表一条活性边，它包含三项内容1.x -当前扫描线与这条边交点的x坐标；2.Δx -该边与当前扫描线交点到下一条扫描线交点的x增量；3.ymax -该边最高顶点相交的扫描线号。

每条扫描线的活性边表中的活性边节点按照各活性边与扫描线交点的x值递增排序连接在一起。

当扫描线y移动到下一条扫描线y = y+1时，活性边表需要更新，即删去不与新扫描线相交的多边形边，同时增加与新扫描线相交的多边形边，并根据增量法重新计算扫描线与各边的交点x。

当多边形新边表ET构成后，按下列步骤进行：①对每一条扫描线i，初始化ET表的表头指针ET[i]；②将ymax = i的边放入ET[i]中；③使y =多边形最低的扫描线号；④初始化活性边表AET为空；⑤循环，直到AET和ET为空。

图形填充之边缘填充算法编译器：VS2013基本思想：基本思想：按任意顺序处理多边形的每条边。

处理时，先求出该边与扫描线的交点，再对扫描线上交点右⽅的所有象素取补。

取补：若该像素是背景⾊,则变为填充⾊; 若像素是填充⾊,则变为背景⾊。

前⾔：刚开始接触这个算法时，⼀直不知道怎么找出直线上任意⼀点x，y的关系，困扰了很久，也和⾼中数学忘了差不多有关，只记得y=kx+b，然⽽这题使⽤(y1-y0)/(x1-x0)=(y-y0)/(x-x0)这样⼀来关系很明显表达出来，⽽且⽤k做的话会存在k不存在的情况，⽽这种做法极端情况是y1=y0，但是这个时候根本不⽤填充，好啦，⽼规矩，附⼀波源码代码：1// 边缘填充算法.cpp : 定义控制台应⽤程序的⼊⼝点。

2//34 #include "stdafx.h"5 #include<stdio.h>6 #include"graphics.h"7 #include<stdlib.h>89//函数声明10int maxX(int a[], int n);//求取最⼤值11void Edgefilling(int a[], int n);12int putcolor(int x, int y);//颜⾊填充1314int main()15 {16int gdriver = DETECT, gmode,n,i;1718 printf("please input the nymber of point:\n");19 scanf_s("%d", &n);2021int *a = (int *)malloc(n*sizeof(int));//动态分配内存2223 printf("input the point:\n");24for (i = 0; i < n; i++)25 scanf_s("%d",&a[i]);2627 initgraph(&gdriver, &gmode, "");2829 setcolor(YELLOW);30 setbkcolor(BLACK);3132 drawpoly(n / 2, a);//画出多边形3334 Edgefilling(a, n);3536 system("pause");37 closegraph();3839return0;40 }4142//边缘填充算法实现43void Edgefilling(int a[],int n)44 {45int i,x,y,Ymax,Ymin;4647for (i = 0; i < n - 2; i = i + 2)48 {49//判断纵坐标⼤⼩50 Ymax = (a[i + 1] > a[i + 3]) ? a[i + 1] : a[i + 3];51 Ymin = (a[i + 1] <= a[i + 3]) ? a[i + 1] : a[i + 3];5253for (y = Ymin; y < Ymax; y++)54 {55 x = (y - a[i + 1])*(a[i + 2] - a[i]) / (a[i + 3] - a[i + 1]) + a[i];5657while (x <= maxX(a, n))58 {59 putpixel(x, y, putcolor(x, y));60 x++;61 }62 }63 }6465 }6667//求取最⼤值68int maxX(int a[],int n)69 {70int i,max=a[0];7172for (i = 0; i < n; i += 2)73 {74if (a[i] > max)75 max = a[i];76 }7778return max;79 }8081//颜⾊填充82int putcolor(int x, int y)83 {84if (getpixel(x, y) == BLACK) 85return BLUE;86else if (getpixel(x, y) == BLUE) 87return BLACK;88else89return YELLOW;90 }结果：。