高一数学幂函数2

高一数学幂函数知识点归纳大全在高一数学学科中，幂函数是重要的一个知识点。

幂函数是指形如y = ax^n的函数，其中a和n是实数，且a≠0，n≠0。

一、幂函数的定义及性质幂函数的定义就是函数的定义，即y = ax^n，其中a称为幂函数的底数，n称为指数。

幂函数的性质有以下几点：1. 当n为正整数时，幂函数表示乘方运算，例如y = 2x^3表示x的3次方。

2. 当n为负整数时，幂函数表示倒数，例如y = 2x^-2表示x的倒数的平方。

3. 当n为分数时，幂函数表示根式，例如y = 2x^(1/2)表示x的平方根。

4. 当n为零时，幂函数表示常数函数，即y = a，其中a为常数。

二、幂函数图像特征1. 当a>0且n为正偶数时，幂函数的图像开口向上，且对称于y轴。

2. 当a>0且n为正奇数时，幂函数的图像开口向上，且不对称于y 轴。

3. 当a<0且n为正偶数时，幂函数的图像开口向下，且对称于y轴。

4. 当a<0且n为正奇数时，幂函数的图像开口向下，且不对称于y 轴。

三、幂函数的变换幂函数可以通过平移、伸缩、翻转等变换得到其他函数形式。

1. 平移：平移是指将函数的图像沿x轴或y轴方向上下左右移动。

例如，对于函数y = 2x^3，将x坐标减2，可以得到y = 2(x-2)^3，实现了向右平移2个单位。

2. 伸缩：伸缩是指将函数的图像沿x轴或y轴方向上下左右拉长或缩短。

例如，对于函数y = 2x^3，将x坐标扩大为原来的2倍，可以得到y = 2(2x)^3，实现了横向的伸缩。

3. 翻转：翻转是指将函数的图像沿x轴或y轴方向上下左右翻转。

例如，对于函数y = 2x^3，将函数的图像上下翻转，可以得到y = -2x^3，实现了关于x轴的翻转。

四、幂函数的应用1. 金融领域：在复利计算中，幂函数常被用于计算投资收益和贷款利息。

2. 自然科学领域：幂函数经常出现在自然界的现象中，如物体的自由落体运动中，下落距离与时间的关系可以用幂函数表示。

《2.3幂函数》教学案例1.教学设计1.1教材的地位和作用《2.3幂函数》是继指数函数和对数函数后学习的另一个基本函数。

幂函数出现在必修一第二章第三节，是基本初等函数之一，是在学生系统学习了函数概念与函数性质之后，进入高中以来遇到的第三种特殊函数，是对函数概念及性质的应用，能培养学生应用性质（定义域，值域，图象，单调性，奇偶性）研究一个函数的意识。

本节课从概念到图象，通过探究归纳出幂函数的性质，让学生再次体会利用信息技术来探索函数的图象和性质，从教材整体安排上来看，学习幂函数是为了让学生进一步了解研究函数的方法，学会利用这种方法去研究其他函数。

因而本节课更是对学生研究函数方法和能力的一个综合提升。

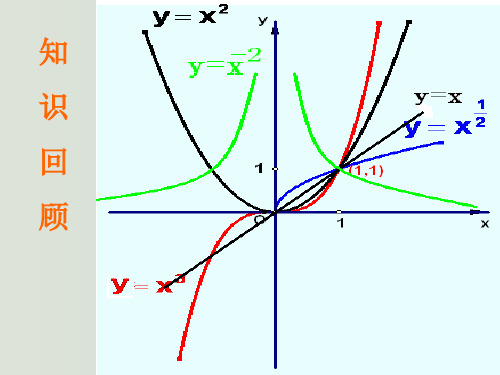
1.2教学目标1.2.1基础知识目标（1）理解幂函数的概念，会画幂函数21132,,,,x y x y x y x y x y =====-的图象，结合这几个幂函数的图象，掌握幂函数的图象变化和性质；（2）能应用幂函数性质解决简单问题。

1.2.2能力训练目标（1）通过观察总结幂函数性质，培养学生抽象概括、逻辑推理和识图能力；（2）使学生进一步体会数形结合思想。

1.3教学重、难点重点：本节的教学重点是从五个具体幂函数中认识幂函数的一些性质。

难点：画五个幂函数的图象并由图象概括其性质是教学中可能遇到的困难。

突破难点：引导学生观察图象，从图象特点入手，观察单调性奇偶性。

1.4学情分析学生学过了一次函数，二次函数，正、反比例函数，指数函数和对数函数，知道了他们的图象和性质，用性质解决一些简单问题也有了一定的基础，为学习幂函数做好了准备，但由于幂函数性质较复杂，学生需要一定的综合分析能力，所以在教学中重视学生自己动手操作、观察分析发现的过程。

我所教的班级是遵义四中高一（23）班，总体学习程度在中等，根据学生的学情，本节课我重在基础，难度上适当适中。

1.5教学用具本节课使用三角板，PPT ，学生准备白纸，格尺。

〖2.3〗幂函数（1）幂函数的定义 一般地，函数y x α=叫做幂函数，其中x 为自变量，α是常数．（2）幂函数的图象（3）幂函数的性质①图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象．幂函数是偶函数时，图象分布在第一、二象限(图象关于y 轴对称)；是奇函数时，图象分布在第一、三象限(图象关于原点对称)；是非奇非偶函数时，图象只分布在第一象限．②过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)． ③单调性：如果0α>，则幂函数的图象过原点，并且在[0,)+∞上为增函数．如果0α<，则幂函数的图象在(0,)+∞上为减函数，在第一象限内，图象无限接近x 轴与y 轴．④奇偶性：当α为奇数时，幂函数为奇函数，当α为偶数时，幂函数为偶函数．当q pα=（其中,p q 互质，p 和q Z ∈），若p 为奇数q 为奇数时，则q py x=是奇函数，若p 为奇数q 为偶数时，则q py x=是偶函数，若p 为偶数q 为奇数时，则qpy x=是非奇非偶函数．⑤图象特征：幂函数,(0,)y x x α=∈+∞，当1α>时，若01x <<，其图象在直线y x =下方，若1x >，其图象在直线y x =上方，当1α<时，若01x <<，其图象在直线y x =上方，若1x >，其图象在直线y x =下方．2.3幂函数的图象及性质1．下列函数中，其定义域和值域不同的函数是( )A ．y ＝x 13 B ．y ＝x －12 C ．y ＝x 53D ．y ＝x 232．如图，图中曲线是幂函数y ＝x α在第一象限的大致图象．已知α取－2，－12，12，2四个值，则相应于曲线C1，C 2，C 3，C 4的α的值依次为( )A ．－2，－12，12，2B ．2，12，－12，－2C ．－12，－2,2，12D ．2，12，－2，－123．以下关于函数y ＝x α当α＝0时的图象的说法正确的是( )A ．一条直线B ．一条射线C ．除点(0,1)以外的一条直线D ．以上皆错 4．函数f(x)＝(1－x)0＋(1－x)12的定义域为________． 5．已知幂函数f(x)的图象经过点(2，22)，则f(4)的值为( ) A ．16 B.116 C.12D ．26．下列幂函数中，定义域为{x|x ＞0}的是( ) A ．y ＝x 23 B ．y ＝x 32 C ．y ＝x －13D ．y ＝x －347．已知幂函数的图象y ＝x m2－2m －3(m ∈Z ，x≠0)与x ，y 轴都无交点，且关于y 轴对称，则m 为( )A ．－1或1B ．－1,1或3C ．1或3D ．3 8．下列结论中，正确的是( )①幂函数的图象不可能在第四象限②α＝0时，幂函数y ＝x α的图象过点(1,1)和(0,0) ③幂函数y ＝x α，当α≥0时是增函数④幂函数y ＝x α，当α<0时，在第一象限内，随x 的增大而减小 A ．①② B ．③④ C ．②③ D ．①④9．在函数y ＝2x 3，y ＝x 2，y ＝x 2＋x ，y ＝x 0中，幂函数有( )A ．1个B ．2个C ．3个D ．4个10．幂函数f(x)的图象过点(3，3)，则f(x)的解析式是________ ．11．函数f(x)＝(m 2－m －5)x m －1是幂函数，且当x ∈(0，＋∞)时，f(x)是增函数，试确定m 的值．12．已知函数f(x)＝(m 2＋2m)·x m2＋m －1，m 为何值时，f(x)是：(1)正比例函数；(2)反比例函数；(3)二次函数；(4)幂函数？13．已知幂函数y ＝x m2－2m －3(m ∈Z)的图象与x 、y 轴都无公共点，且关于y 轴对称，求m 的值，并画出它的图象．答案1. 解析：选D.y ＝x 23＝3x 2，其定义域为R ，值域为[0，＋∞)，故定义域与值域不同． 2.解析：选B.当x ＝2时，22＞212＞2－12＞2－2，即C 1：y ＝x 2，C 2：y ＝x 12，C 3：y ＝x －12，C 4：y ＝x －2.3.解析：选C.∵y ＝x 0，可知x≠0，∴y ＝x 0的图象是直线y ＝1挖去(0,1)点．4.解析：⎩⎪⎨⎪⎧1－x≠01－x≥0，∴x<1.答案：(－∞，1)5 解析：选C.设f(x)＝x n ，则有2n ＝22，解得n ＝－12，即f(x)＝x －12，所以f(4)＝4－12＝12.6 解析：选D.A.y ＝x 23＝3x 2，x ∈R ；B.y ＝x 32＝x 3，x≥0；C.y ＝x －13＝13x，x≠0；D.y ＝x－34＝14x 3，x ＞0.7 解析：选B.因为图象与x 轴、y 轴均无交点，所以m 2－2m －3≤0，即－1≤m≤3.又图象关于y 轴对称，且m ∈Z ，所以m 2－2m －3是偶数，∴m ＝－1,1,3.故选B.8 解析：选D.y ＝x α，当α＝0时，x≠0；③中“增函数”相对某个区间，如y ＝x 2在(－∞，0)上为减函数，①④正确．9 解析：选B.y ＝x 2与y ＝x 0是幂函数．10 解析：设f(x)＝x α，则有3α＝3＝312⇒α＝12.答案：f(x)＝x 1211 解：根据幂函数的定义得：m 2－m －5＝1，解得m ＝3或m ＝－2，当m ＝3时，f(x)＝x 2在(0，＋∞)上是增函数；当m ＝－2时，f(x)＝x －3在(0，＋∞)上是减函数，不符合要求．故m ＝3.12 解：(1)若f(x)为正比例函数，则⎩⎪⎨⎪⎧m 2＋m －1＝1m 2＋2m≠0⇒m ＝1. (2)若f(x)为反比例函数，则⎩⎪⎨⎪⎧m 2＋m －1＝－1m 2＋2m≠0⇒m ＝－1. (3)若f(x)为二次函数，则⎩⎪⎨⎪⎧m 2＋m －1＝2m 2＋2m≠0⇒m ＝－1±132.(4)若f(x)为幂函数，则m 2＋2m ＝1，∴m ＝－1±213 解：由已知，得m 2－2m －3≤0，∴－1≤m≤3. 又∵m ∈Z ，∴m ＝－1,0,1,2,3.当m ＝0或m ＝2时，y ＝x －3为奇函数，其图象不关于y 轴对称，不适合题意． ∴m ＝±1或m ＝3.当m ＝－1或m ＝3时，有y ＝x 0，其图象如图(1)．当m ＝1时，y ＝x －4，其图象如图(2)．.。

4.1.3 幂函数知识点01幂函数的定义一般地，形如y=x α的函数称为幂函数，其中x 是自变量，α为常数．注 (1)注意幂函数中x α的系数是1，底数是变量x ，指数α是常数；【即学即练1】下列是幂函数的是()A.y =2xB. y =3x 4C.y =x 2D.y =(x ―1)3知识点02 幂函数图像及其性质(1) 幂函数y =x,y =x 2,y =x 3,y =x 12,y =x ―1的图象．(2) 幂函数y =x,y =x 2,y =x 3,y =x 12,y =x ―1的性质y =x y =x 2y =x 3y=x 12y =x ―1图象定义域RR R[0,+∞)x ≠0值域R [0,+∞)R [0,+∞)x ≠0奇偶性奇函数偶函数奇函数非奇非偶奇函数单调性在R 上递增在(―∞,0]上递减在(0,+∞)上递增在R 上递增在[0,+∞)上递增在(―∞,0)上递减在(0,+∞)上递减特殊点(1,1),(0,0)(1,1),(0,0)(1,1),(0,0)(1,1),(0,0)(1,1)(3)性质① 所有的幂函数在(0 , +∞ )都有定义，并且图象都过点(1 , 1)；② α>0时，幂函数的图象通过原点，并且在[0 , +∞ )上是增函数．特别地，当α>1时，幂函数变化快，图象下凹；当0<α<1时，幂函数变化慢，图象上凸.Eg y =x 12图象上凸，y =x 2图象下凹，在[0 , +∞ )上是增函数．③ α<0时，幂函数的图象在(0 , +∞ )上是减函数．在第一象限内，当x 从右边趋向原点时，图象在y 轴右方无限地逼近y 轴正半轴，当x 趋于+∞时，图象在x 轴上方无限地逼近x 轴正半轴．Eg y=x―1=1，x【即学即练2】已知幂函数y=x p3(p∈Z)的图象关于y轴对称，如图所示，则（）A．p为奇数，且p>0B．p为奇数，且p<0 C．p为偶数，且p>0D．p为偶数，且p<0【题型一：判断函数是否是幂函数】例1．现有下列函数：①y=x3；②y=4x2；③y=x5+1；④y=(x―1)2；⑤y=x，其中幂函数的个数为（）A．4B．3C．2D．1变式1-1．下列函数是幂函数的是（ ）A．y=2x B．y=2x―1C．y=(x+1)2D．y=变式1-2．下列函数中，y=1x3，y=2x+1，y=x3+x，y=）A．1B．2C．3D．4【方法技巧与总结】1 幂函数的概念：一般地，形如y=xα的函数称为幂函数，其中x是自变量，α为常数．2 注意幂函数中xα的系数是1，底数是变量x，指数α是常数.【题型二：求幂函数的值】例2．已知幂函数f(x)=(m+2)x n的图象经过点(4,2)，则m―n=（）A．―3B．―52C．―2D．―32变式2-1．已知幂函数y=f(x)的图象经过点4,f(2)等于（）A．12B．2C D变式2-2．已知幂函数f(x)=(m―1)x m2―1，则f(―1)=（）A．―1B．1C．―2D．2变式2-3．若幂函数f(x)=xα的图象过点(2,8)，则g(x)=α―x+）A．―∞B．[2,+∞)C+∞D．(―∞,2]【方法技巧与总结】1 求幂函数的解析式，可利用待定系数法；2 已给幂函数解析式形式求参数，注意幂函数的系数为1.【题型三：幂函数的定义域】例3．已知幂函数f(x)=x―m2+2m的定义域为R，且m∈Z，则m的值为（）A．―1B．0C．1D．2变式3-1．下列幂函数中，定义域为(0,+∞)的是（ ）A．y=x23B．y=x32C．y=x―23D．y=x―32变式3-2．幂函数f(x)图象过点y=f(x)+f(2―|x|)的定义域为（）A．(0,2)B．(0,2]C．[0,2]D．(―2,2)【方法技巧与总结】1 掌握常见幂函数y=x,y=x2,y=x3,y=x12,y=x―1的图象与性质；2 求非常见幂函数的定义域，常把幂函数的解析式中幂的形式化为根式的形式更好理解；3 所有的幂函数在(0 , +∞ )都有定义，若幂函数f(x)=x a中a<0时定义域内不含0，若幂函数f(x)=x m n=为整数)中n是偶数，则函数定义域不能取(―∞,0)。

高一上必修二第四章《指数函数、对数函数与幂函数》知识点梳理§4.4　幂函数学习目标　1.了解幂函数的概念.2.掌握y ＝x α(α＝－1，12，1，2，3)的图像与性质.3.理解和掌握幂函数在第一象限的分类特征，能运用数形结合的方法处理幂函数的有关问题．知识点一　幂函数的概念一般地，函数y ＝x α称为幂函数，其中x 是自变量，α是常数．提醒　幂函数中底数是自变量，而指数函数中指数为自变量．知识点二　幂函数的图像和性质1．幂函数的图像在同一平面直角坐标系中，幂函数y ＝x ，y ＝x 2，y ＝x 3，y ＝，y ＝x －1的图像如图．2．五个幂函数的性质y ＝xy ＝x 2y ＝x 3y ＝y ＝x －1定义域R R R [0，＋∞){x |x ≠0}值域R [0，＋∞)R [0，＋∞){y |y ≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在R 上是增函数在[0，＋∞)上是增函数，在(－∞，0]上是减函数在R 上是增函数在[0，＋∞)上是增函数在(0，＋∞)上是减函数，在(－∞，0)上是减函数12x 12x公共点(1,1)1．y ＝－1x 是幂函数．(　×　)2．当x ∈(0,1)时，x 2>x 3.(　√　)3．y ＝与y ＝定义域相同．(　×　)4．若y ＝x α在(0，＋∞)上为增函数，则α>0.(　√　)一、幂函数的概念例1　(1)(多选)下列函数为幂函数的是( )A ．y ＝x 3 B ．y ＝(12)xC ．y ＝4x 2D ．y ＝x答案　AD解析　B 项为指数函数，C 中的函数的系数不为1，AD 为幂函数．(2)已知y ＝(m 2＋2m －2)＋2n －3是幂函数，求m ，n 的值．解　由题意得Error!解得Error!或Error!所以m ＝－3或1，n ＝32.反思感悟　判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y ＝x α(α为常数)的形式，即函数的解析式为一个幂的形式，且需满足：(1)指数为常数；(2)底数为自变量；(3)系数为1.跟踪训练1　已知f (x )＝ax 2a ＋1－b ＋1是幂函数，则a ＋b 等于( )A ．2 B ．1 C.12 D ．0答案　A解析　因为f (x )＝ax 2a ＋1－b ＋1是幂函数，所以a ＝1，－b ＋1＝0，即a ＝1，b ＝1，则a ＋b ＝2.32x 64x 22m x二、幂函数的图像例2　如图所示，图中的曲线是幂函数y ＝x n 在第一象限的图像，已知n 取±2，±12四个值，则对应于c 1，c 2，c 3，c 4的n 依次为( )A ．－2，－12，12，2B ．2，12，－12，－2C ．－12，－2,2，12D ．2，12，－2，－12答案　B解析　根据幂函数y ＝x n 的性质，故c 1的n ＝2，c 2的n ＝12，当n <0时，|n |越大，曲线越陡峭，所以曲线c 3的n ＝－12，曲线c 4的n ＝－2.反思感悟　解决幂函数图像问题应把握的两个原则(1)依据图像高低判断幂指数大小，相关结论为：在(0,1)上，指数越大，幂函数图像越靠近x 轴(简记为指大图低)；在(1，＋∞)上，指数越大，幂函数图像越远离x 轴(简记为指大图高)．(2)依据图像确定幂指数α与0,1的大小关系，即根据幂函数在第一象限内的图像(类似于y ＝x －1 或y ＝或y ＝x 3)来判断．跟踪训练2　函数f (x )＝的大致图像是( )答案　A解析　因为－12<0，所以f (x )在(0，＋∞)上单调递减，排除选项B ，C ；又f (x )的定义域为(0，＋∞)，故排除选项D.三、比较幂值的大小12x 12x例3　比较下列各组数中两个数的大小：(1)(25)0.5与(13)0.5；(2)(－23)－1与(－35)－1；(3)与.解　(1)∵幂函数y ＝x 0.5在(0，＋∞)上是单调递增的，又25>13，∴(25)0.5>(13)0.5.(2)∵幂函数y ＝x －1在(－∞，0)上是单调递减的，又－23<－35，∴(－23)－1>(－35)－1.(3)∵函数y 1＝(23)x为R 上的减函数，又34>23，∴>.又∵函数y 2＝在(0，＋∞)上是增函数，且34>23，∴>，∴>.反思感悟　比较幂值大小的方法跟踪训练3　比较下列各组值的大小：(1)，；(2)，，1.42.解　(1)∵y ＝为R 上的偶函数，∴＝.又函数y ＝为[0，＋∞)上的增函数，且0.31<0.35，3423⎛⎫⎪⎝⎭2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭3423⎛⎫ ⎪⎝⎭23x 2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭2334⎛⎫ ⎪⎝⎭3423⎛⎫⎪⎝⎭()650.31-650.35121.2121.465x ()650.31-650.3165x∴<，即<.(2)∵y ＝在[0，＋∞)上是增函数，且1.2<1.4，∴<.又∵y ＝1.4x 为增函数，且12<2，∴<1.42，∴<<1.42.幂函数性质的应用典例　已知幂函数y ＝x 3m －9 (m ∈N ＋)的图像关于y 轴对称且在(0，＋∞)上单调递减，求满足的a 的取值范围．解　因为函数y ＝x 3m －9在(0，＋∞)上单调递减，所以3m －9<0，解得m <3.又因为m ∈N ＋，所以m ＝1,2.因为函数的图像关于y 轴对称，所以3m －9为偶数，故m ＝1.则原不等式可化为.因为y ＝在(－∞，0)，(0，＋∞)上单调递减，所以a ＋1>3－2a >0或3－2a <a ＋1<0或a ＋1<0<3－2a ，解得23<a <32或a <－1.故a 的取值范围是Error!.[素养提升]　(1)幂函数y ＝x α中只有一个参数α，幂函数的所有性质都与α的取值有关，故可由α确定幂函数的定义域、值域、单调性、奇偶性，也可由这些性质去限制α的取值．(2)通过具体实例抽象出幂函数的概念和性质，并应用单调性求解，体现了数学中数学运算与直观想象的核心素养．650.31650.35()650.31-650.3512x 121.2121.4121.4121.2121.433(1)(32)m m a a --+<-1133(1)(32)a a --+<-13x-1．下列函数是幂函数的是( )A ．y ＝5x B ．y ＝x 5C ．y ＝5x D ．y ＝(x ＋1)3答案　B解析　函数y ＝5x 是指数函数，不是幂函数；函数y ＝5x 是正比例函数，不是幂函数；函数y ＝(x ＋1)3的底数不是自变量x ，不是幂函数；函数y ＝x 5是幂函数．2．幂函数y ＝x α(α∈R )的图像一定不经过( )A ．第四象限 B ．第三象限C ．第二象限 D ．第一象限答案　A解析　由幂函数的图像可知，其图像一定不经过第四象限．3．设α∈{－1，1，12，3}，则使函数y ＝x α的定义域为R 且为奇函数的所有α值为( )A ．1,3B ．－1,1C ．－1,3D ．－1,1,3答案　A解析　可知当α＝－1,1,3时，y ＝x α为奇函数，又因为y ＝x α的定义域为R ，则α＝1,3.4．已知幂函数f (x )＝kx α(k ∈R ，α∈R )的图像过点(12，2)，则k ＋α等于( )A.12 B ．1 C.32 D ．2答案　A解析　∵幂函数f (x )＝kx α(k ∈R ，α∈R )的图像过点(12，2)，∴k ＝1，f(12)＝(12)α＝2，即α＝－12，∴k ＋α＝12.5．已知f (x )＝，若0<a <b <1，则下列各式中正确的是( )A ．f (a )<f (b )<f(1a )<f(1b)B ．f (1a )<f(1b )<f (b )<f (a )C ．f (a )<f (b )<f (1b )<f(1a )D ．f (1a )<f (a )<f(1b )<f (b )12x答案　C解析　因为函数f (x )＝在(0，＋∞)上是增函数，又0<a <b <1<1b <1a ，故f (a )<f (b )<f(1b )<f(1a).1．知识清单：(1)幂函数的概念．(2)幂函数的图像．(3)幂函数的性质及其应用．2．方法归纳：数形结合．3．常见误区：幂函数与指数函数的区别；幂函数的奇偶性．1．幂函数f (x )＝x α的图像经过点(2,4)，则f (－12)等于( )A.12B.14 C ．－14 D ．2答案　B解析　幂函数f (x )＝x α的图像经过点(2,4)，则2α＝4，解得α＝2；∴f (x )＝x 2，∴f (－12)＝(－12)2＝14.2．下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的函数是( )A ．y ＝x －2 B ．y ＝x －1C ．y ＝x 2 D ．y ＝答案　A解析　所给选项都是幂函数，其中y ＝x －2和y ＝x 2是偶函数，y ＝x －1和y ＝不是偶函数，故排除选项B ，D ，又y ＝x 2在区间(0，＋∞)上单调递增，不合题意，y ＝x －2在区间(0，＋∞)上单调递减，符合题意．3．设a ＝，b ＝，c ＝，则a ，b ，c 的大小关系是( )12x 13x13x 2535⎛⎫ ⎪⎝⎭3525⎛⎫⎪⎝⎭2525⎛⎫⎪⎝⎭A ．a >c >bB ．a >b >cC ．c >a >bD ．b >c >a答案　A解析　∵y ＝(x >0)为增函数，又35>25，∴a >c .∵y ＝(25)x (x ∈R )为减函数，又25<35，∴c >b .∴a >c >b .4．在同一坐标系内，函数y ＝x a (a ≠0)和y ＝ax －1a的图像可能是( )答案　C解析　选项A 中，幂函数的指数a <0，则y ＝ax －1a 应为减函数，A 错误；选项B 中，幂函数的指数a >1，则y ＝ax －1a 应为增函数，B 错误；选项D 中，幂函数的指数a <0，则－1a >0，直线y ＝ax －1a在y 轴上的截距为正，D 错误．5．若幂函数f (x )的图像过点(2，2)，则函数g (x )＝f (x )－3的零点是( )A.3 B ．9 C ．(3，0) D ．(9,0)答案　B解析　∵幂函数f (x )＝x α的图像过点(2，2)，∴f (2)＝2α＝2，解得α＝12，∴f (x )＝，∴函数g (x )＝f (x )－3＝－3，由－3＝0，得x ＝9.∴函数g (x )＝f (x )－3的零点是9.6．已知幂函数f (x )＝x α的部分对应值如表：x11225x 12x 12x 12xf (x )122则f (x )的单调递增区间是________．答案　[0，＋∞)解析　因为f(12)＝22，所以(12)α＝22，即α＝12，所以f (x )＝的单调递增区间是[0，＋∞)．7．已知幂函数f (x )＝x α(α∈R )的图像经过点(8,4)，则不等式f (6x ＋3)≤9的解集为________．答案　[－5,4]解析　由题意知8α＝4，故α＝log 84＝23，由于f (x )＝＝x 2为R 上的偶函数且在(0，＋∞)上递增，故f (6x ＋3)≤9即为f (6x ＋3)≤f (27)，所以|6x ＋3|≤27，解得－5≤x ≤4.8．设a ＝，b ＝，c ＝，则a ，b ，c 从小到大的顺序是________．答案　b <a <c解析　由a ＝，b ＝，可利用幂函数的性质，得a >b ，可由指数函数的单调性得c >a ，∴b <a <c .9．已知幂函数f (x )＝x α的图像过点P (2，14)，试画出f (x )的图像并指出该函数的定义域与单调区间．解　因为f (x )＝x α的图像过点P (2，14)，所以f (2)＝14，即2α＝14，得α＝－2，即f (x )＝x －2，f (x )的图像如图所示，定义域为(－∞，0)∪(0，＋∞)，单调递减区间为(0，＋∞)，单调递增区间为(－∞，0)．10．已知幂函数f (x )＝x 9－3m (m ∈N ＋)的图像关于原点对称，且在R 上单调递增．(1)求f (x )的解析式；(2)求满足f (a ＋1)＋f (3a －4)<0的a 的取值范围．解　(1)由幂函数f (x )＝x 9－3m (m ∈N ＋)的图像关于原点对称，且在R上单调递增，可得9－3m >0，解得m <3，m ∈N ＋，可得m ＝1,2，12x 23x 2312⎛⎫⎪⎝⎭2315⎛⎫ ⎪⎝⎭1312⎛⎫⎪⎝⎭2312⎛⎫ ⎪⎝⎭2315⎛⎫⎪⎝⎭若m ＝1，则f (x )＝x 6的图像不关于原点对称，舍去；若m ＝2，则f (x )＝x 3的图像关于原点对称，且在R 上单调递增，成立．则f (x )＝x 3.(2)由(1)可得f (x )是奇函数，且在R 上单调递增，由f (a ＋1)＋f (3a －4)<0，可得f (a ＋1)<－f (3a －4)＝f (4－3a )，即为a ＋1<4－3a ，解得a <34.11．若函数f (x )＝(m ＋2)x a 是幂函数，且其图像过点(2,4)，则函数g (x )＝ log a (x ＋m )的单调递增区间为( )A ．(－2，＋∞) B ．(1，＋∞)C ．(－1，＋∞) D ．(2，＋∞)答案　B解析　由题意得m ＋2＝1，解得m ＝－1，则f (x )＝x a ，将(2,4)代入函数的解析式得，2a ＝4，解得a ＝2，故g (x )＝log a (x ＋m )＝log 2(x －1)，令x －1>0，解得x >1，故g (x )在(1，＋∞)上单调递增．12．函数y ＝－1的图像关于x 轴对称的图像大致是( )答案　B解析　y ＝的图像位于第一象限且为增函数，所以函数图像是上升的，函数y ＝－1的图像可看作由y ＝的图像向下平移一个单位长度得到的(如选项A 中的图所示)，将y ＝－1的图像关于x 轴对称后即为选项B.13．为了保证信息的安全传输，有一种密钥密码系统，其加密、解密原理为：发送方由明文到密文(加密)，接收方由密文到明文(解密)．现在加密密钥为y ＝x α(α为常数)，如“4”通过加密后得到密文“2”．若接收方接到密文“3”，则解密后得到的明文是________．答案　9解析　由题意可知加密密钥y ＝x α(α为常数)是一个幂函数，所以要想求得解密后得到的明文，就必须先求出α的值．由题意，得2＝4α，解得α＝12，则y ＝.由＝3，得x ＝9，即明文是9.14．已知幂函数f (x )＝，若f (a ＋1)<f (10－2a )，则a 的取值范围是________．12x 12x 12x 12x 12x 12x 12x 12x答案　(3,5)解析　∵f (x )＝＝1x(x >0)，易知f (x )在(0，＋∞)上为减函数，又f (a ＋1)<f (10－2a )，∴Error!解得Error!∴3<a <5.15.幂函数y ＝x α，当α取不同的正数时，在区间[0,1]上它们的图像是一族美丽的曲线(如图)．设点A (1,0)，B (0,1)，连接AB ，线段AB 恰好被其中的两个幂函数y ＝x α，y ＝x β的图像三等分，即有BM ＝MN ＝NA ，那么，αβ等于________．答案　1解析　由条件，得M (13，23)，N (23，13)，可得13＝(23)α，23＝(13)β，即α＝13，β＝23.所以αβ＝13·23＝lg 13lg 23·lg 23lg 13＝1.16．已知幂函数g (x )过点(2，12)，且f (x )＝x 2＋ag (x )．(1)求g (x )的解析式；(2)讨论函数f (x )的奇偶性，并说明理由．解　(1)设幂函数的解析式g (x )＝x α(α为常数)．因为幂函数g (x )过点(2，12)，所以2α＝12，解得α＝－1，所以g (x )＝1x.(2)由(1)得f (x )＝x 2＋a x.①当a ＝0时，f (x )＝x 2.12x 23log 13log 23log 13log由于f(－x)＝(－x)2＝x2＝f(x)，可知f(x)为偶函数．②当a≠0时，由于f(－x)＝(－x)2＋a－x＝x2－ax≠x2＋ax＝f(x)，且f(－x)＝(－x)2＋a－x＝x2－ax≠－(x2＋a x)＝－f(x)，所以f(x)是非奇非偶函数．综上，①当a＝0时，f(x)为偶函数；②当a≠0时，f(x)为非奇非偶函数．。