定积分高考题

简单已测：424次正确率：91.8 %1.定积的值是（ ）A.B.C.D.考点：⽤定义求定积分、微积分基本定理求定积分知识点：定积分的概念、微积分基本定理答案：D 解析：，故选：．⼀般已测：3296次正确率：69.9 %2.计算（ ）A.B.C.D.考点：利⽤定积分的⼏何意义解题、微积分基本定理求定积分知识点：定积分的概念、定积分的⼏何意义答案：B解析：选⼀般已测：4642次正确率：87.5 %3.若,,则,,的⼤⼩关系为( )A.B.C.D.考点：⽤定义求定积分、微积分基本定理求定积分知识点：定积分的基本性质、定积分的常⽤结论答案：B解析：由于,,,且,所以，故选.⼀般已测：3883次正确率：75.3 %4.若,则( )2xdx ∫0212342xdx =x =4∫202∣∣∣∣20D (1−cos x )dx =∫− 2π2ππ+2π−2π−2(1−cos x )dx=(x −sin x )∫− 2π2π =π−2.∣∣∣∣ 2π− 2πB .S = x dx 1∫122S = dx 2∫12x 1S =e dx 3∫12x S 1S 2S 3S <S <S 123S <S <S 213S <S <S 231S <S <S321S = x dx = x ∣ = − = 1∫12231312383137S = dx =lnx ∣ =ln 22∫12x 112S = e dx =e ∣ =e −e 3∫12x x 122ln 2< <e −e 372S <S <S 213B f (x )=x +2 f (x )dx 2∫01 f (x )dx=∫01A.B.C.D.考点：微积分基本定理求定积分、运⽤定积分的相关性质解题知识点：被积函数的原函数、微积分基本定理答案：B解析：令(常数),则,所以,解得,故选:.中等已测：4750次正确率：71.2 %5.在如图所⽰平⾯直⻆坐标系中,正⽅形的边⻓为,曲线是函数图象位于正⽅形内的部分,直线恰好是函数在处的切线,现从正⽅形内任取⼀点,那么点取⾃阴影部分的概率等于（ ）A.B.C.D.考点：利⽤定积分的⼏何意义解题、微积分基本定理求定积分知识点：曲边梯形的⾯积、定积分的⼏何意义答案：D解析：正⽅形的边⻓为,由函数,得,则,得.⼜当时,,可得,曲线的解析式为,阴影部分⾯积.点取⾃阴影部分的概率等于.故选:.−1−31 311f (x )dx =m ∫01f (x )=x +2m 2m = f (x )dx =( x +2mx ) = +2m ∫01313∣∣0131m =− 31B OABC 1m y =a (x −1)+b 2AC y=a (x −1)+b 2x =0P P1213141 61∵OABC 1,∴S =1正方形OABC y =a (x −1)+b 2y =2a (x −1)′y ∣ =−2a =−1′x =0a =21x=0y =a +b =1b = 21∴m y = (x −1)+ 21221∴S = [ (x −1)+ −(−x +1)]dx = x dx = x ∣=∫0121221∫012126130161∴P 61D⼀般已测：4665次正确率：92.6 %6.已知,则⼆项式的展开式中的系数为（ ）A.B.C.D.考点：利⽤定积分的性质解题、微积分基本定理求定积分知识点：定积分的概念、微积分基本定理答案：C 解析：,的展开式的通项公式为,令得,,展开式中的系数为.⼀般已测：2948次正确率：92.5 %7.实数使得复数是纯虚数,则的⼤⼩关系是（ ）A.B.C.D.考点：⽤定义求定积分、⽤所求定积分的⼏何意义求定积分知识点：定积分的概念、复数的概念答案：C解析：,它为纯虚数,所以,表⽰单位圆的四分之⼀的⾯积为,所以,应选.中等已测：3726次正确率：56.3 %8.若，则=（ ）A.B.a = dx ∫ e 1e x1(1− )x a 5x −316080−80−160∵a= dx =lne −ln =2∫ e 1e x 1e 1∴(1−)=(1−)xa 5x25T=C (−2)x r +15r r −r −r=−3r =3∴x −3C (−2)=−80533a1−i a +i b = xdx ,c= dx ∫01∫011−x 2a ,b ,c a <b <c a <c <b b <c <a c <b <a= = 1−i a +i1−i 1+i ()()a +i 1+i ()()2a −1+a +1i ()a =1,b = xdx = ∣ = ,c = dx ∫012x 20121∫011−x 2 4πb <c <a C f x + f x dx =x ()∫01() f x dx ∫01()41 21C.D.考点：⽤定义求定积分、利⽤定积分的性质解题知识点：定积分的基本性质、基本积分公式答案：A 解析：由，则，则，，则，故选A ．⼀般已测：2708次正确率：72.5 %9.⼀个⼈骑⻋以⽶/秒的速度匀速追赶停在交通信号灯前的汽⻋,当他离汽⻋⽶时，交通信号灯由红变绿,汽⻋开始做变速直线⾏驶(汽⻋与⼈的前进⽅向相同),若汽⻋在时刻的速度⽶/秒，那么此⼈（ ）．A.可在秒内追上汽⻋B.不能追上汽⻋,但其间最近距离为⽶C.不能追上汽⻋,但其间最近距离为⽶D.不能追上汽⻋,但其间最近距离为⽶考点：⼆次函数的单调性、利⽤定积分的⼏何意义解题知识点：微积分基本定理、基本积分公式答案：D解析：设该⼈骑⻋⾏驶距离和汽⻋⾏驶距离的差为，则，所以，所以该⼈不能追上汽⻋，但其间最近距离为⽶⼀般已测：391次正确率：82.7 %10.甲、⼄两⼈从同⼀起点出发按同⼀⽅向⾏⾛，已知甲、⼄⾏⾛的速度与⾏⾛的时间分别为，(如图)，当甲⼄⾏⾛的速度相同(不为零)时刻( )A.甲⼄两⼈再次相遇B.甲⼄两⼈加速度相同12fx +f x dx =x ()∫01()f x =x − f x dx ()∫01() fx dx = x − f x dx dx∫01()∫01(∫01())= xdx − f x dx dx = − f x dx ∫01∫01[∫01()]21∫01()∴ f x dx = − f x dx ∫01()21∫01() f x dx =∫01()41625t v (t )=t 716147S (t )S (t )= 6−t dt =6t −t ∫0t()212S (t ) =S (6)=36−18=18max 7v =甲t v =t 乙2C.甲在⼄前⽅D.⼄在甲前⽅考点：微积分基本定理求定积分、运⽤定积分的相关性质解题知识点：定积分的物理意义、变速运动问题答案：C解析：由，得，解得(舍)，或．由．．所以当甲⼄⾏⾛的速度相同(不为零)时刻甲在⼄前⽅．故选：．中等已测：1818次正确率：73.8 %11.已知，若函数满⾜，则称为区间上的⼀组``等积分''函数，给出四组函数：①②；③；④函数分别是定义在上的奇函数且积分值存在.其中为区间上的“等积分”函数的组数是( )A.B.C.D.考点：利⽤定积分的⼏何意义解题、微积分基本定理求定积分知识点：定积分的基本性质、微积分基本定理答案：C解析：本题是新定义问题，主要考查对定义的理解和定积分的计算.对于①，⽽,所以①是⼀组“等积分”函数；对于②，,⽽,所以②不是⼀组``等积分''函数；对于③，函数的图像是以原点为圆⼼，为半径的半圆，故,⽽,所以③是⼀组``等积分''函数；对于④，由于函数分别是定义在上的奇函数且积分值存在，利⽤奇函数的图像关于原点对称和定积分的⼏何意义，可以求得函数的定积分,所以④是⼀组``等积分''函数.故选.简单已测：3293次正确率：86.3 %12..v =v 甲乙 =t t 2t =0t =1 dt = t ∣ = ∫01t 32 230132 t dt = t ∣= ∫0123130131C a <b f (x ),g (x ) f (x )dx = g (x )dx ∫a b∫a bf (x ),g (x )[a ,b ]f (x )=2∣x ∣,g (x )=x +1;f (x )=sinx ,g (x )=cosx f (x )=,g (x )= πx 1−x 2432f (x ),g (x )[−1,1][−1,1]1234f x dx = 2x dx = 2−x dx + 2xdx =2,∫−11()∫−11∣∣∫−10()∫01g x dx = x +x ∣ =2∫−11()(212)−11 f (x )dx = sinxdx =0∫−11∫−11 g x dx = cos xdx =2sin 1≠0∫−11()∫−11f (x )1 f x dx = dx = ∫−11()∫−111−x 22πg x dx = πx ∣ = ∫−11()413−112πf (x ),g (x )[−1,1] f (x )dx = g x dx =0∫−11∫−11()C (sinx +cosx )dx =∫− 2π2π考点：⽤定义求定积分、微积分基本定理求定积分知识点：定积分的概念、被积函数的原函数答案：解析：；故填.⼀般已测：4543次正确率：94.5 %13..考点：利⽤定积分的⼏何意义解题知识点：定积分的概念、定积分的⼏何意义答案：解析：函数即：，表⽰以为圆⼼，为半径的圆在轴上⽅横坐标从到的部分，即四分之⼀圆，结合定积分的⼏何意义可得．故答案为．⼀般已测：2478次正确率：65.4 %14.⼀辆汽⻋在⾏驶中由于遇到紧急情况⽽刹⻋，以速度⾏驶⾄停⽌，在此期间汽⻋继续⾏驶的距离是.考点：定积分在求⾯积中的应⽤、微积分基本定理求定积分知识点：定积分的物理意义、基本积分公式答案：解析：本题考查定积分的概念.令，化为,⼜,解得.汽⻋继续⾏驶的距离.⼀般已测：4698次正确率：91.6 %15.若正实数满⾜,则的最⼩值为.考点：利⽤基本不等式求最值、利⽤公式求定积分知识点：定积分的基本性质、基本积分公式答案：解析：由题意得;即,所以(当且仅当时等号成⽴).所以,即的最⼩值为.简单已测：1192次正确率：87.8 %16.有⼀⾮均匀分布的细棒，已知其线密度为，棒⻓为，则细棒的质量.考点：⽤定义求定积分、微积分基本定理求定积分2(sinx +cosx )dx =−cosx +sinx ∣ ∫− 2π 2π()−2π2π=1+1=22 ( )dx ∫121−(x −1)2=4πy=1−(x −1)2(x −1)+y =1(x ≥1,y ≥0)22(1,0)1x 12 ( )dx = ×π×1=∫121−(x −1)24124π 4πv (t )=7−3t +1+t 254+25ln 5v (t )=7−3t + =01+t253t −4t −32=02t >0t =4S = (7−3t + )dt =(7t − t +25ln (1+t ))∣ =4+25ln 5∫041+t 2523204m ,n + = (x +)dx m 2n 1∫−22π14−x 2log (m +2n )22(x + )dx = dx = × π×2=2∫−22π14−x 2π1∫−224−x 2π1212 + =2m 2n 1m +2n =(m +2n )( + )= + +2≥2 +2=4m 12n 1m 2n 2n m × m 2n 2n m m =2n log m +2n ≥log 4=22()2log (m +2n )22ρx =x ()32M =(1)(2)知识点：定积分的物理意义、定积分的常⽤结论答案：解析：依题意有：.⼀般已测：3051次正确率：65.2 %17.在区间上给定曲线.试在此区间内确定点的值,使图中的阴影部分的⾯积与之和最⼩,并求最⼩值．考点：导数在最⼤值、最⼩值问题中的应⽤、定积分在求⾯积中的应⽤知识点：利⽤导数求函数的最值、微积分基本定理答案：时,最⼩,且最⼩值为解析：⾯积等于边⻓分别为与的矩形⾯积去掉曲线与轴、直线所围成的⾯积,即.的⾯积等于曲线与轴,,围成的⾯积去掉矩形边⻓分别为,⾯积,即.所以阴影部分的⾯积．令,得或.时,；时,；时,.所以当时,最⼩,且最⼩值为.⼀般已测：401次正确率：92.8 %18.已知．求的单调区间；求函数在上的最值．考点：利⽤导数研究函数的单调性、利⽤导数求闭区间上函数的最值知识点：函数单调性和导数的关系、利⽤导数求函数的最值(1)答案：单调调增区间是,单调递减区间是．解析：依题意得,,定义域是．,令,得或； 令得,且函数定义域是,函数的单调增区间是,单调递减区间是．(2)答案：最⼤值是,最⼩值是．解析：由(1)知函数在区间上为减函数,区间上为增函数, 且,在上的最⼤值是,最⼩值是．4x dx= ∣ =4∫0234x 402[0,1]y =x 2t S 1S 2t=21S (t )41S 1t t 2y =x 2x x =t S =t ⋅t − x dx = t 12∫0t 2323S 2y =x 2x x =t x =1t 21−t S = x dx −t (1−t )= t −t + 2∫t 122323231S (t )=S +S = t −t + (0≤t ≤1)12343231S (t )=4t −2t =4t (t − )=0′221t =0t = 21t =0S (t )= 31t = 21S (t )= 41t =1S (t )= 32t = 21S (t )41F (x )= (t +2t −8)dt ,(x >0)∫0x2F (x )F (x )[1,3](2,+∞)(0,2)F (x )= (t +2t −8)dt =( t +t−8t )∣ = x +x −8x ∫0x 231320x 3132(0,+∞)(1)F (x )=x +2x −8′2F (x )>0′x >2x <−4F (x )<0,′−4<x <2(0,+∞)∴F (x )(2,+∞)(0,2)F (3)=−6F (2)=− 328F (x )(0,2)(2,3)F (1)=− ,F (2)=− ,F (3)=−6320328∴F (x )[1,3]F (3)=−6F (2)=− 328(1)(2)中等已测：3275次正确率：52.7 %19.已知⼆次函数，直线，直线(其中，为常数)，若直线,与函数的图象以及,、轴与函数的图象所围成的封闭图形(阴影部分)如图所⽰.求,,的值；求阴影⾯积关于的函数的解析式.考点：求函数解析式的常⽤⽅法、利⽤定积分的⼏何意义解题知识点：⼆次函数的解析式、⼆次函数的图象(1)答案：, , 解析：由图形可知⼆次函数的图象过点，，并且的最⼤值为，则解得，函数的解析式为.(2)答案：解析：由得,,,,直线与的图象的交点坐标为由定积分的⼏何意义知：.f (x )=ax +bx +c 2l :x =21l :y =−t +8t 220≤t ≤2t l 1l 2f (x )l 1l 2y f (x )a b c S t S (t )a=−1b =8c =0(0,0)(8,0)f (x )16 ⎩⎨⎧c =0,a ⋅8+b ⋅8+c =02=164a 4ac −b 2 ⎩⎨⎧a =−1b =8c =0∴f (x )f (x )=−x +8x 2S (t )=− t +10t −16t + 3432340{ y =−t +8t 2y =−x +8x2x −8x −t (t −8)=02∴x =t 1x =8−t 2∵0≤t ≤2∴l 2f (x )(t ,−t +8t )2S (t )= −t +8t −−x +8x dx + [(−x +8x )−(−t +8t )]dx ∫0t [(2)(2)]∫t 222=[(−t +8t )x −(− +4x )]∣ +[(− +4x )−(−t +8t )x ]∣ 23x 320t 3x 322t 2=− t +10t −16t + 3432340。

专练15 定积分与微积分基本定理命题范围：积分的概念与运算、微积分基本定理．[基础强化]一、选择题1.⎠⎛12(x －2)d x 的值为( )A ．－1B ．0C ．1D ．－122．若f(x)＝x 2＋2⎠⎛01f(x)d x ，则⎠⎛01f(x)d x ＝( )A .－1B ．－13C ．13D ．13．直线y ＝4x 与曲线y ＝x 3在第一象限内围成的封闭图形的面积为( )A ．22B ．4 2C ．2D ．44．若a ＝⎠⎛02x 2d x ，b ＝⎠⎛02x 3d x ，c ＝⎠⎛02sin x d x ，则a ，b ，c 的大小关系是( )A ．a<c<bB ．a<b<cC ．c<b<aD ．c<a<b5.⎠⎛－11(1－x 2＋sin x)d x ＝( )A ．π4B ．π2C ．πD ．π2＋26．设k ＝⎠⎛0π(sin x －cos x)d x ，若(1－kx)8＝a 0＋a 1x ＋a 2x 2＋…＋a 8x 8，则a 1＋a 2＋…＋a 8＝( )A .－1B ．0C ．1D ．2567．设f(x)＝⎩⎨⎧1－x 2，x∈[－1，1），x 2－1，x∈[1，2]，则⎠⎛－12f(x)d x 的值为( )A .π2＋43B ．π2＋3C ．π4＋43D ．π4＋38．如图是函数y ＝cos (2x －5π6)在一个周期内的图像，则阴影部分的面积是( )A ．34B ．54C ．32D ．32－349．已知等差数列{a n }中，a 5＋a 7＝⎠⎛0πsin x d x ，则a 4＋2a 6＋a 8的值为( )A ．8B ．6C ．4D ．2二、填空题10．[2022·安徽滁州二模]设f(x)＝e x，则⎠⎛01[f′(x)＋2x]d x________．11．曲线y ＝x 2与直线y ＝x 所围成的封闭图形的面积为________.12．已知函数f(x)＝x 3＋ax 2＋bx(a ，b∈R )的图像如图所示，它与直线y ＝0在原点处相切，此切线与函数图像所围区域(图中阴影部分)的面积为274，则a 的值为________.13．[2022·西藏拉萨中学月考]由曲线y ＝x ，直线y ＝x －2及y 轴所围成的平面图形的面积为________．14．[2022·甘肃张掖期末]如图，在矩形ABDC 中，AB ＝1，AC ＝2，O 为AC 中点，抛物线的一部分在矩形内，点O 为抛物线顶点，点B ，D 在抛物线上，在矩形内随机地放一点，则此点落在阴影部分的概率为________．15．[2022·宁夏石嘴山一模]⎠⎛－11(e x＋|x|)d x ＝________．16．[2022·黑龙江一模]在棱长为2的正方体ABCD­A 1B 1C 1D 1的侧面ABB 1A 1内有一动点P 到直线A 1B 1与直线BC 的距离相等，则在侧面ABB 1A 1上动点P 的轨迹与棱AB 、BB 1所围成的图形面积是________．专练15 定积分与微积分基本定理1．D ⎠⎛12(x －2)d x ＝⎝ ⎛⎭⎪⎫12x 2－2x |21 ＝12×22－2×2－⎝ ⎛⎭⎪⎫12－2＝－12.2．B 令⎠⎛01f(x)d x ＝m ，则f(x)＝x 2＋2m ，∴⎠⎛01f(x)d x ＝⎠⎛01x 2d x ＋⎠⎛012m d x ＝(13x 2＋2mx)|10＝m ，得m ＝－13.3．D 由⎩⎪⎨⎪⎧y ＝4x ，y ＝x 3，得x ＝0或x ＝2或x ＝－2(舍)， ∴S＝⎠⎛02(4x －x 3)d x ＝⎝ ⎛⎭⎪⎫2x 2－14x 4|20 ＝4.4．D a ＝⎠⎛02x 2d x ＝13x 3|20 ＝83，b ＝⎠⎛02x 3d x ＝14x 4|20 ＝4，c ＝⎠⎛02sin x d x ＝(－cos x )|20 ＝1－cos2，∵1－cos2<83<4，∴c <a <b .5．B ⎠⎛－11(1－x 2＋sin x )d x ＝⎠⎛－111－x 2d x ＋⎠⎛－11sin x d x ，∵y ＝sin x 为奇函数，∴⎠⎛－11sin x d x ＝0，又⎠⎛－111－x 2d x 表示以坐标原点为圆心，以1为半径的上半个圆的面积，∴⎠⎛－111－x 2d x＝π2， ∴⎠⎛－11( 1－x 2＋sin x )d x ＝π2.6．B 因为k ＝⎠⎛0π(sin x －cos x )d x ＝⎠⎛0πsin x d x －⎠⎛0πcos x d x ＝－cos x |π0 －sin x |π0 ＝2，所以(1－kx )8＝(1－2x )8＝a 0＋a 1x ＋a 2x 2＋…＋a 8x 8.令x ＝1，得a 0＋a 1＋a 2＋…＋a 8＝(1－2)8＝1，令x ＝0，得a 0＝1，所以a 1＋a 2＋…＋a 8＝(a 0＋a 1＋a 2＋…＋a 8)－a 0＝1－1＝0.故选B.7．A ⎠⎛－12f(x)d x ＝⎠⎛－111－x 2d x ＋⎠⎛12(x 2－1)d x ＝12π×12＋(13x 3－x)|21 ＝π2＋43.故选A .8．B S ＝－∫π60cos (2x －5π6)d x ＋∫2π3π6cos (2x －5π6)d x＝－⎣⎢⎡⎦⎥⎤12sin （2x －5π6）|π60＋[12sin (2x －5π6)]|2π3π6＝－[12sin (－π2)－12sin (－5π6)]＋[12sin π2－12sin (－π2)]＝14＋1＝54.故选B .9．C ∵a 5＋a 7＝⎠⎛0πsin x d x ＝(－cos x)|π0 ＝－(cosπ－cos 0)＝2，又{a n }为等差数列， ∴a 5＋a 7＝2a 6＝2，∴a 6＝1， ∴a 4＋2a 6＋a 8＝4a 6＝4. 10．e解析：因为f(x)＝e x， 所以错误!错误!0＝e ＋1－1＝e . 11.16解析：如图，阴影部分的面积即为所求．解⎩⎪⎨⎪⎧y ＝x 2，y ＝x ，得⎩⎪⎨⎪⎧x ＝0，y ＝0或⎩⎪⎨⎪⎧x ＝1，y ＝1，则A(1，1). 故所求面积为S ＝⎠⎛01(x －x 2)d x ＝(12x 2－13x 3)|10 ＝16.12．－3解析：由已知得f′(0)＝0，因为f′(x)＝3x 2＋2ax ＋b ，所以b ＝0，则f(x)＝x 3＋ax 2，令f(x)＝0，得x 1＝0，x 2＝－a.由切线y ＝0与函数图像所围区域(题图中阴影部分)的面积为274，得 －⎠⎛0－a f(x)d x ＝274，即－⎠⎛0－a (x 3＋ax 2)d x ＝274，即－(14x 4＋a 3x 3)－a 0 ＝274，所以－⎣⎢⎡⎦⎥⎤a 44＋a3×（－a ）3＝274，即a 412＝274，解得a ＝±3，由题图可知a<0，∴a＝－3. 13.163解析：由定积分知 S ＝⎠⎛4x －(x －2)d x ＝(23x 32－12x 2＋2x)|1＝(23×8－8＋8)－0＝163. 14.13解析：由题可知矩形面积为2，建立如图所示的平面直角坐标系，则抛物线方程为y 2＝2x(0≤x≤1)， 抛物线及BD 围成的面积为2(1－⎠⎛01x d x)＝23，点落在阴影部分的概率为232＝13.15．e －1e＋1解析：⎠⎛－11(e x＋|x|)d x ＝⎠⎛－1(e x－x)d x ＋⎠⎛01(e x＋x)d x ＝(e x－x 22)|0－1 ＋(e x ＋x 22)|10 ＝(e－0)[e －1－（－1）22]＋(e 1＋122)－[e 0＋0]＝1－1e ＋12＋e ＋12－1＝e －1e ＋1.16.43解析：以点A 为坐标原点，AB 、AD 、AA 1所在直线分别为x 、y 、z 轴建立如图所示的空间直角坐标系，设点P(x ，0，z)，则0≤x≤2，0≤z≤2，则点P 到直线A 1B 1的距离为2－z ， 因为BC⊥平面AA 1B 1B ，BP ⊂平面AA 1B 1B ， 所以，BC⊥BP，所以，点P 到直线BC 的距离为|BP →|＝（x －2）2＋z 2， 由已知可得（z －2）2＋z 2＝2－z ，化简可得z ＝x －x24，当x ＝2时，z ＝1，即点P 的轨迹交棱BB 1于点(2，0，1)，因此，在侧面ABB 1A 1上动点P 的轨迹与棱AB 、BB 1所围成的图形面积是⎠⎛02(x －x 24)d x ＝(12x 2－x 312)|20 ＝43.。

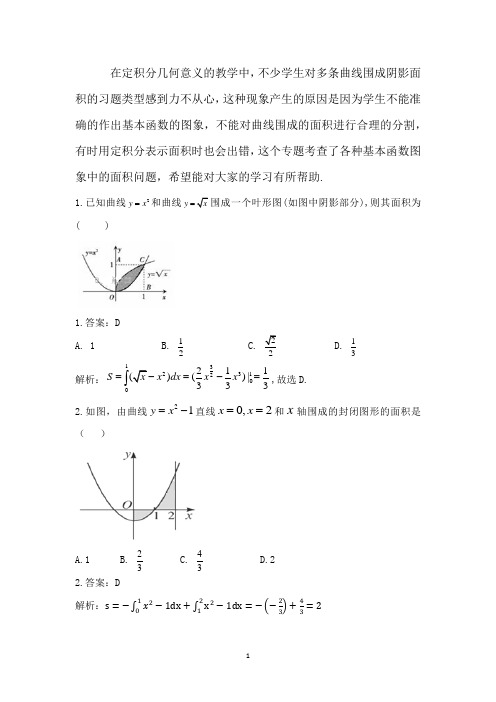
在定积分几何意义的教学中，不少学生对多条曲线围成阴影面积的习题类型感到力不从心，这种现象产生的原因是因为学生不能准确的作出基本函数的图象，不能对曲线围成的面积进行合理的分割，有时用定积分表示面积时也会出错，这个专题考查了各种基本函数图象中的面积问题，希望能对大家的学习有所帮助.1.已知曲线2y x =和曲线y =围成一个叶形图(如图中阴影部分),则其面积为( )1.答案：D A. 1B. 12C.2D. 13解析：13231200211)()|333S x dx x x =-=-=⎰,故选D. 2.如图，由曲线21y x =-直线0,2x x ==和x 轴围成的封闭图形的面积是（ ）A.1B.23 C. 43 D.22.答案：D解析：s =−∫x 210−1dx +∫x 221−1dx =−(−23)+43=23.曲线()2sin 0y x x π=≤≤与直线1y =围成的封闭图形的面积为( )A. 43πB. 23πC. 43πD. 23π+3.答案：B解析：由()2sin 0y x x π=≤≤,直线1y =. 令2sin 1x =，可得：6x π=或56π. ∴曲线()2sin 0y x x π=≤≤与直线1y =交于点,16A π⎛⎫ ⎪⎝⎭和5,16B π⎛⎫⎪⎝⎭.因此,围成的封闭图形的面积()5665262sin 12cos 36S x dx x xπππππ=-=--=-⎰. 4.片叶子由曲线2||y x =与曲线2||y x =围成，则每片叶子的面积（ ）A ．16BC ．13D ．234.答案：C 解析：s =∫(√x−x 2)dx =(23x 32−13x 3)|0110=135.已知曲线e =x y ，直线1x =及41y x =-+围成的封闭图形的面积为（ ）A ．e 1+B ．eC ． e 1-D ．1e 8-5.答案：B解析：s =∫(e x +4x −1)dx =(e x +2x 2−x )|0110=e6.如图,由曲线sin y x =,0x =,32x π=与x 轴围成的阴影部分的面积是__________.6.答案：3 解析：s =∫sinxdx−∫sinxdx 3π2π=(−cosx )|0ππ0+cosx|π3π2=37.由曲线11y x =-直线1y x =-及3y =所围成的封闭图形的面积为( ) A.2ln3- B.2ln3+ C.4ln3- D.4ln3+7.答案：C解析：封闭图形如图,计算得4,3,(2,1),(3,3)3A B C ⎛⎫⎪⎝⎭2432113224ln3312S dx x =⨯-+⨯⨯=--⎰,故选C.8.由曲线e x y =，e x y -=以及1x =所围成的图形的面积等于（ ） A.2 B.2e 2- C.12e - D.1e 2e+-8.答案：D解析：曲线e ,e x x y y -==和直线1x =围成的图形面积， 就是()10e e x x dx --⎰()1102x xe e e e --=+=+-.故选：D 。

定积分复习题1. 下列等于1的积分是（ ） A ．dx x ⎰10 B ．dx x ⎰+10)1( C ．dx ⎰101 D ．dx ⎰1021 2． dx e e x x ⎰-+10)(= （ ）A ．ee 1+ B ．2e C ．e 2 D ．e e 1- 3． 曲线]23,0[,cos π∈=x x y 与坐标轴围成的面积 （ ）A ．4B ．2C ．25D ．3 4、由直线与曲线y=cosx 所围成的封闭图形的面积为（ ） A 、 B 、1 C 、 D 、5、由曲线y=x 2，y=x 3围成的封闭图形面积为（ ）A 、B 、C 、D 、6、由曲线xy=1，直线y=x ，y=3所围成的平面图形的面积为（ ）A 、B 、2﹣ln3C 、4+ln3D 、4﹣ln37、从如图所示的正方形OABC 区域内任取一个点M （x ，y ），则点M 取自阴影部分的概率为（ ）A 、B 、C 、D 、 8、⎰+10)2(dx x e x 等于（ ） A 、1B 、e ﹣1C 、eD 、e 2+1 9、dx x ⎰421等于（ ）A 、﹣2ln2B 、2ln2C 、﹣ln2D 、ln2 A 、π B 、2C 、π﹣2D 、π+2 10、已知则⎰-a a xdx cos =)0(21>a ，则⎰a xdx 0cos =（ ） A 、2 B 、1 C 、 D 、11、曲线y=x 2+2与直线y=3x 所围成的平面图形的面积为（ ）A 、B 、C 、D 、112、下列计算错误的是（ ）A 、0sin =⎰-ππxdx B 、3210=⎰dx xC 、⎰⎰=-2022cos 2cos πππxdx xdx D 、0sin 2=⎰-ππxdx 13、计算⎰-2024dx x 的结果是（ ）A 、4πB 、2πC 、πD 、14、若0)32(02=-⎰dx x x k，则k 等于（ ）A 、0B 、1C 、0或1D 、以上均不对15、曲线y=x 2和曲线y=围成一个叶形图（阴影部分），其面积是（ ）A 、1B 、C 、D 、16、在113)23(x x -的展开式中任取一项，设所取项为有理项的概率为p ,则dx x p ⎰10=( ) A 1 B 76 C 67 D 131117. 计算dx x ⎰-+22)cos 1(ππ的值为（ ）A ．πB ．2C ．2π-D ．2π+18、已知1220()(2)f a ax a x dx =⎰-，则()f a 的最大值是A ．23 B ．29 C ．43 D ．4919. 由直线1x =，x=2，曲线sin y x =及x 轴所围图形的面积为A ．πB ．sin 2sin1-C ．sin1(2cos11)-D ．21cos12cos 1+-20. 22-⎰的值是A ．2πB ．πC ．2πD ．4π21. 给出下列四个结论：①⎰=π200sin xdx ；②命题“2,0"x R x x ∃∈->的否定是“2,0x R x x ∀∈-≤”；③“若22,am bm < 则a b <”的逆命题为真；④集合}1)(|{},014|{2<-=<--=a x x B x x x A ，则“)3,2(∈a ”是“A B ⊆”充要条件. 则其中正确结论的序号为A.①③ B.①② C.②③④ D.①②④22. 设函数()m f x x ax =+的导函数'()21f x x =+，则21()f x dx -⎰的值等于( )A.56B.12C.23D.1623、如图中阴影部分的面积是（ ）A 、B 、C 、D 、24、由曲线x y =，直线2-=x y 及y 轴所围成的图形的面积为（ ） A 、 B 、4 C 、 D 、625、设)(x f y =为区间[0，1]上的连续函数，且恒有1)(0≤≤x f ，可以用随机模拟方法近似计算积分⎰10)(dx x f ，先产生两组（每组N 个）区间[0，1]上的均匀随机数x 1，x 2，…x N 和y 1，y 2，…y N ，由此得到N 个点（x i ，y i ）（i=1，2，…，N ），再数出其中满足)(i i x f y ≤（i=1，2，…，N ）的点数N 1，那么由随机模拟方案可得积分⎰10)(dx x f 的近似值为 ．26、如图所示，计算图中由曲线22x y =与直线2=x 及x 轴所围成的阴影部分的面积S= ．27、由曲线和直线y=x ﹣4，x=1，x=2围成的曲边梯形的面积是 ．28、从如图所示的长方形区域内任取一个点M （x ，y ），则点M 取自阴影部分部分的概率为 ．29、设函数f （x ）=ax 2+c （a≠0），若)()(010x f dx x f =⎰，0≤x 0≤1，则x 0的值为 ．30、由三条曲线y=x 2，4y=x 2，y=1 所围图形的面积 ．31、由曲线y 2=2x 和直线y=x ﹣4所围成的图形的面积为 ．。

高三数学积分试题1.．【答案】【解析】=.考点:定积分2.定积分的值为（）A．B．C．D．【答案】C【解析】，故选C.【考点】定积分.3.直线在第一象限内围成的封闭图形的面积为（）A．B．C．D．4【答案】D【解析】由已知得，，故选D.【考点】定积分的应用.4. [2014·汕头模拟]设f(x)＝，则等于()A．B．C．D．不存在【答案】C【解析】本题画图求解，更为清晰，如图，＝＋＝x3＋(2x－x2)＝＋(4－2－2＋)＝.5.直线l过抛物线C：x2＝4y的焦点且与y轴垂直，则l与C所围成的图形的面积等于() A．B．2C．D．【答案】C【解析】由C：x2＝4y，知焦点P(0,1)．直线l的方程为y＝1.所求面积S＝＝＝.6.已知二次函数的图象如图所示，则它与轴所围图形的面积为（）A．B．C．D．【答案】B【解析】根据图像可得：，再由定积分的几何意义，可求得面积为．7.设函数的图象与直线轴所围成的图形的面积称为在上的面积，则函数上的面积为．【答案】【解析】用积分表示面积.【考点】定积分8.设，若曲线与直线，，所围成封闭图形的面积为2，则（）A．2B．e C．2e D．【答案】D【解析】，∴.【考点】定积分.9.已知t>0,若(2x-1)dx=6,则t的值等于()A．2B．3C．6D．8【答案】B【解析】(2x-1)dx=2xdx-1·dx=x2-x=t2-t,由t2-t=6得t=3或t=-2(舍去).【方法技巧】定积分的计算方法(1)利用定积分的几何意义,转化为求规则图形(三角形、矩形、圆或其一部分等)的面积.(2)应用微积分基本定理:求定积分f(x)dx时,可按以下两步进行,第一步:求使F'(x)=f(x)成立的F(x);第二步:计算F(b)-F(a).10.已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为,则a的值为.【答案】-1【解析】f'(x)=-3x2+2ax+b,∵f'(0)=0,∴b=0,∴f(x)=-x3+ax2,令f(x)=0,得x=0或x=a(a<0).=-(-x3+ax2)dx=a4=,∴a=-1.S阴影11.________．【答案】1【解析】.【考点】定积分的应用.12.dx + .【答案】+1【解析】，，所以的图像是半圆，由定积分的几何意义可知，所以。

【高考数学】定积分的概念、基本定理及其简单应用10未命名一、单选题1．定义{},min ,,a a b a b b a b ≤⎧=⎨>⎩，则由函数21()min ,f x x x ⎧⎫=⎨⎬⎩⎭的图象与x 轴、直线2x =所围成的封闭图形的面积为 A ．712B ．512C ．1ln 26+ D ．1ln 23+ 【答案】D 【解析】由题意2(01)()1,1x x f x x x⎧<≤⎪=⎨>⎪⎩ ，做出函数图象如下：交点(1,1)A ，作垂线交x 轴于点(1,0)D 图中阴影部分为所求，可分别用积分求出两部分面积的和1122231001111ln ln 233S x dx dx x x x =+=+=+⎰⎰，选D.2．设f (x )＝则f(x)d x 等于( )A ．B ．C ．D ．不存在【答案】C 【解析】当12231001101,(),|.33x f x x x dx x ≤≤===⎰当222111112,()2,(2)(2)|,22x f x x x dx x x ≤≤=--=-=⎰故1115().326f x dx =+=⎰ 故选C ．3．在平面直角坐标系中，记抛物线 与x 轴所围成的平面区域为 ，该抛物线与直线y ＝ (k ＞0)所围成的平面区域为 ，向区域 内随机抛掷一点 ，若点 落在区域 内的概率为，则k 的值为（ ）A ．B ．C ．D ．【答案】A 【解析】试题分析：易知抛物线 开口向下，对称轴为.令 ，得 或1.所以抛物线 与x 轴所围成的平面区域 即抛物线 在x 轴上方的部分,其面积为.联立得抛物线与直线y ＝ (k ＞0)的交点为（0,0）和 .因为该抛物线与直线y ＝ (k ＞0)所围成的平面区域为 ，向区域 内随机抛掷一点 ，若点 落在区域 内的概率为.所以交点 应该在区域 内，即 ，所以 .区域 面积为.由点 落在区域 内的概率为得，，.考点：定积分的应用、几何概型4．设函数()mf x x ax =+的导函数()'21f x x =+，则()21f x dx -⎰的值等于 ( )A ．56B ．12C ．23D ．16【答案】A 【解析】由于()mf x x ax =+的导函数()()2'21,f x x f x x x =+∴=+，于是()()222322111115|326f x dx x x dx x x ⎛⎫-=-=-= ⎪⎝⎭⎰⎰，故选A. 5．如图，由曲线21y x =-，直线0,2x x ==和x 轴围成的封闭图形的面积是（ ）A ．22(1)x dx -⎰B ．22(1)x dx -⎰C ．2201x dx-⎰D ．122211(1)(1)x dx x dx --+-⎰⎰【答案】C 【解析】阴影部分面积为()()1222011d 1d x x x x ⎡⎤--+-⎣⎦⎰⎰，而222101|1|112x x x x x ，，，，⎧-≤≤-=⎨-<≤⎩ 故选C.点睛：1.求曲边图形面积的方法与步骤 (1)画图，并将图形分割为若干个曲边梯形；(2)对每个曲边梯形确定其存在的范围，从而确定积分的上、下限； (3)确定被积函数；(4)求出各曲边梯形的面积和，即各积分的绝对值的和．2．利用定积分求曲边图形面积时，一定要找准积分上限、下限及被积函数．当图形的边界不同时，要分不同情况讨论． 6．设(){},|0,01A x y x m y =<<<<， s 为()e 1n+的展开式的第一项（e 为自然对数的底数），m =若任取(),a b A ∈，则满足1ab >的概率是( )A ．2e B ．1eC ．e 2e- D ．e 1e- 【答案】C 【解析】由题意得，n s e =，则m e =，即0a e <<，01b <<，如图所示，作曲线()101a b b =<<，交直线1,b a e ==于点()11A ，，1,B e e ⎛⎫ ⎪⎝⎭，则满足事件1ab >的实验区域为曲边形ABC ，其面积为111112eS e dx e e x⎛⎫=⋅--=- ⎪⎝⎭⎰，所以所求概率为221e e P e e--==⨯，故选C.7．已知()2a cosx dx π=-⎰，则912ax ax ⎛⎫+ ⎪⎝⎭展开式中，3x 项的系数为（ ） A ．638B ．212- C ．6316D ．638- 【答案】B 【解析】()20a cosx dx π=-⎰=20 |sinx π-=﹣1，则二项式912ax ax ⎛⎫+ ⎪⎝⎭的展开式的通项公式为T r+1=﹣9r C •921•2rrx -⎛⎫ ⎪⎝⎭， 令9﹣2r=3，求得r=3， ∴展开式中x 3项的系数为﹣39C •18=﹣212-， 故选：C8．1(2)xe x dx +⎰等于（ ）A ．eB ．1C ．1e -D ．1e +【答案】A 【解析】()()()()121002|110.x x e x dx e xe e ⎰+=+=+-+= 本题选择A 选项.9．⎰= （ ）A ．2πB ．12π- C ．4π D ．142π-【解析】先设1sin ,[,0]1sin 2x t t x t π-=∈-⇒=+，则cos dx tdt =，所以2222111cos (1cos 2)+sin2t|22244tdt t dt πππππ---==+=⨯=⎰⎰，应选答案C 。

【高考数学】定积分的概念、基本定理及其简单应用4未命名一、单选题1．如图所示,在边长为1的正方形OABC 内任取一点P,用M 表示事件“点P 恰好取自曲线2y x =与直线1y =及y 轴所围成的曲边梯形内”,N 表示事件“点P 恰好取自阴影部分内”,则P(N | M)等于( )A ．14B ．15C ．16D ．17【答案】A 【解析】 【分析】根据条件概率的公式得到()()P(N | M)=P MN P M ,由微积分定理分别计算得到()()120=.1x S P MN S x x d =-⎰阴影阴影，，()()120=1-.1x SP M S x d =⎰曲边梯形曲边梯形，两式作比即可得到结果. 【详解】根据条件概率的公式得到()()P(N | M)=P MN P M()P MN 表示落在阴影部分的概率，()()121=.16x S P MN S x x d =-=⎰阴影阴影， ()()1202=1-.13x S P M S x d ==⎰曲边梯形曲边梯形， ()()116P(N | M)=.243P MN P M == 故答案为A.【点睛】这个题目考查了几何概型的应用以及条件概率的公式，涉及微积分定理的应用，属于中档题；在利用几何概型的概率公式来求其概率时，几何“测度”可以是长度、面积、体积、角度等，其中对于几何度量为长度，面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的，而对于角度而言，则是过角的顶点的一条射线落在Ω的区域（事实也是角）任一位置是等可能的． 2．已知113()2eem dx x -+=⎰，则m 的值是（ ） A ．14e e- B ．12C ．12-D ．1-【答案】C 【解析】 【分析】先求定积分，再解方程得结果. 【详解】因为113()(ln )112ee e m dx x mx em m x-+=+=+-=⎰， 所以12m =-，选C. 【点睛】本题考查定积分，考查基本分析求解能力，属基础题..3．由曲线 ， 以及 所围成的图形的面积等于（ ）. A ． B ．C ．D ．【答案】D 【解析】分析：先求出曲线 的交点，得到积分下限，利用定积分表示出图形面积，最后利用定积分的定义进行求解即可.详解：曲线 的交点坐标为 ，由曲线 以及 围成的图形的面积，就是，故选D.点睛：本题主要考查定积分的几何意义，属于中档题.一般情况下，定积分的几何意义是介于 轴、曲线 以及直线 之间的曲边梯形面积的代数和，其中在轴上方的面积等于该区间上的积分值，在轴下方的面积等于该区间上积分值的相反数,所以在用定积分求曲边形面积时，一定要分清面积与定积分是相等还是互为相反数；两条曲线之间的面积可以用两曲线差的定积分来求解.4．如图，矩形中曲线的方程分别是，.，，在矩形内随机取一点，则此点取自阴影部分的概率为( )A．B．C．D．【答案】B【解析】【分析】先由微积分基本定理，计算出阴影部分的面积，再求出矩形的面积，由几何概型的概率计算公式，即可求出结果.【详解】由题意可得，当时，由可得；所以，阴影又矩形，所以在矩形内随机取一点，则此点取自阴影部分的概率为. 故选B【点睛】本题主要考查与面积有关的几何概型，熟记概率计算公式以及微积分基本定理即可，属于常考题型.5．如图，在矩形中的曲线是，的一部分，点，，，在矩形内随机取一点，则此点取自阴影部分的概率是（）A ．B ．C ．D ．【答案】B 【解析】 【分析】利用定积分求出阴影部分的面积再与矩形ABCD 面积之比即可得出答案。

高考数学定积分与微积分基本定理选择题1. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值2. 下列关于定积分与微积分基本定理的说法错误的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值3. 下列关于定积分与微积分基本定理的说法错误的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值4. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值5. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值6. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值7. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值8. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值9. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值10. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值11. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值12. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值13. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值14. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值15. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值16. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值17. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值18. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值19. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值20. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值21. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值22. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值23. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值24. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值25. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值26. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值27. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值28. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值29. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值30. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值31. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值32. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值33. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值34. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值35. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值36. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值37. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值38. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值39. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值40. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值41. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值42. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值43. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值44. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值45. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值46. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值47. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值48. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值49. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值50. 下列关于定积分与微积分基本定理的说法正确的是（）A. 定积分可以用来求解曲线下的面积B. 定积分与不定积分互为逆运算C. 定积分与不定积分可以互相转化D. 定积分可以用来求解函数的极值。