最新浙教版九年级数学下册1.1锐角三角函数公开课优质PPT课件(12)

AB A. sinA B. sinB C. tanA D. tanB 2.如图，已知在 Rt△ABC 中，∠C＝90°，AC＝4，tanA＝1，则 BC 的长是( )
2 A. 2 B. 8 C. 2 5 D. 4 5
3.在△ABC 中，∠C＝90°，AB＝2，AC＝1，则 sinB 的值是( )
A. 1 2
B. 2 2
C. 3 2
D. 2
4.如图，在△ABC 中，∠C＝90°，BC∶AC＝1∶2，则 sinA＝___.
5.如图，在Rt△ABC中，∠C＝90°，b＝20，c＝20， 则∠B的度数为________．
6.如图，在△ABC 中，∠ABC＝90°，BD⊥AC 于点 D，∠CBD＝α，AB＝3，BC＝4， 求 sinα，cosα，tanα的值．
B
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系?
(2) BC 和 B1C1 , AC 和 AC1 ，
AB AB1 AB AB1
BC 和 B1C1有什么关系?
AC AC1
(3)如果改变B在AB1上的位置呢?
A
C
想一想
B
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系?
1.1 锐角三角函数（1）
复习回顾
勾股定理
?当直角三角形的锐角不是
直 角
特殊角度时，三边之间是否
三
也有类似的定值数量关系呢？
角
形
想一想
B
A
C
B1 (1)直角三角形AB1C1和直角三角形ABC 有什么关系? (2) BC 和 B1C1 , AC 和 AC1 ，
AB AB1 AB AB1
BC 和 B1C1有什么关系?

铅 直 高 度
水平宽度
梯子在上升变陡的过程中，倾 斜角，铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化？
铅 直 高 度
水平宽度
梯子在上升变陡的过程中，倾 斜角，铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化？
铅 直 高 度
水平宽度
梯子在上升变陡的过程中，倾 斜角，铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化？
铅 直 高 度
水平宽度
梯子越陡——倾斜角＿越＿＿大＿＿
倾斜角越大——铅直高度与梯子的比＿越＿＿大＿＿ 倾斜角越大——水平宽度与梯子的比＿越＿＿小＿＿
倾斜角越大——铅直高度与水平宽度
的比＿越＿＿大＿＿
铅 直 高
度
水平宽度
想一想
B
A
C
B1
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
(2)
B C 和 B 1C 1
A B AB1
, A C 和 A C 1,
AB
AB1
BC AC
和 B 1 C 1 有什么关系?
AC 1
(3)如果改变B在梯子上的位置
呢?
C1
想一想
B
B1
C
取宝物比赛
10m
10m
（1）
1m
5m
（2）
谈谈今天的收获
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
作业
1.书本作业题第6题 2.同步练习

回味无穷
▪ 定义中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A 的正切,习惯省去“∠”号； 3.sinA,cosA,tanA, 是一个比值.注意比的顺序, 且sinA,cosA,tanA, 均﹥0,无单位. 4.sinA,cosA,tanA, 的大小只与∠A的大小有关, 而与直角三角形的边长无关. 5.角相等,则其三角函数值相等；两锐角的三角函
(2) BC和 B1C1 , AC 和 AC1, BC
AB AB1 AB AB1 AC
和 B1C1有什么关系?
AC1
BC B1C1
=
AB AB1
AC AC1
=
AB AB1
BC B1C1
=
AC AC1
C1
想一想
B
ß
A
C
(1)直角三角形AB1C1和直角三 角 形ABC有什么关相系似?
B1 (2) BC 和 B1C1 , AC 和 AC1, BC
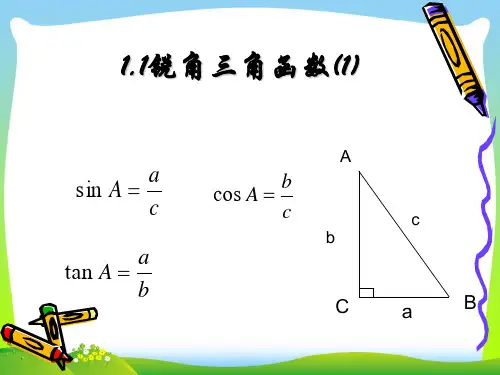
1、sinA 不是一个角 2、sinA不是 sin与A的乘积 3、 sinA 是一个比值 4、sinA 没有单位
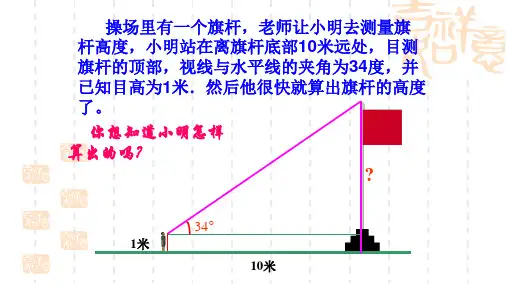
▪ 求出图19.3.3所示的Rt△ABC中∠A的三个三 角函数值.
8
15
图 19.3.1
例2 如图:在Rt△ABC中 ,∠B=900,AC=200,sinA=0.6.求:BC的长.
C 200
值变了吗？
对于锐角A的每一个确定的值，其对 边与斜边、邻边与斜边、邻边与对边 的比值也是惟一确定的
这几个比值都是锐角∠A的函数，记
作sin A、cos A、tan A，即

w2 一辆汽车沿着一山坡行驶了100m,
34
2
5
其铅直高度上升了50m.求山坡与水平
6
面所成的锐角的大小.
7
w3. 图中的螺旋形由一系列直角三角形组
成.每个三角形都不得是以点O为一顶点.
w(1)求∠A0OA1,∠A1OA2,∠A2OA3,的大小. w(2)已知∠An-1OAn,是一个小于200的角,求 n的值.tanA7O8A 180.353, 6∴∠A7OA8=19.470.∴n=8.
sinABC101. AC 40 4
w那么A是多少 度呢? w要解决这问题,我们可以借助科学计算器.
w请与同伴交流你是怎么做的?
做一做 3
知识在于积累
w已知三角函数值求角度,要用到三个键, sin cos tan 和第二功能键Sin-1 cos-1 tan-1 和2ndf .
w例如,
SinA=0.9816 CosA=0.8607 tanA=0.1890
∴V型角的大小约550.
学化
呀!
随堂练习 7
真知在00m,其铅直高度 上升了50m.求山坡与水平面所成的锐角的大小.
咋办
?
w老师期望: w你具有成功的把握.
例题欣赏 5
行家看“门道”
w例2 如图,一名患者体内某重要器官后面有一肿瘤.
在接受放射性治疗时,为了最大限度地保证疗效,并且
tanA=56.78
按键的顺序 2ndf Sin-1 0 . 9 8 1 6 = 2ndf cos-1 0 . 8 6 0 7 = 2ndf tan-1 0 . 1 8 9 0 = 2ndf tan-1 5 6 . 7 8 =
显示结果
Sin-1=0.9816 =78.99184039 coS-1=0.8607 =30.60473007 tan-1=0.1890 =10.70265749

AC 5 5
sin B AC 5 ，cosB BC 2，tan B AC 5 .
AB 3
AB 3
BC 2
延伸：由上面的计算，你能猜想∠A，∠B的正弦、余弦值 有什么规律吗？
结论：一个锐角的正弦等于它余角的余弦，或一个锐角的 余弦等于它余角的正弦.
请同学们拿出
自己的学习工具— 1
2
—一副三角尺，思
AB 5
BC 3
2、 如图，在Rt△ABC中，∠C＝90°，BC=2，
AB=3，求∠A，∠B的正弦、余弦、正切值． B
解：在RtABC中，
3
2
AC AB2 BC2 32 22 5,
A
C
sin A BC 2，cos A AC 5 ，tan A BC 2 2 5 .
AB 3
AB 3
c 斜边
B
a 对边
A
bC
例如，当∠A＝30°时，我们有
sin A sin 30 1 2
当∠A＝45°时，我们有
sin A sin 45 2 2
在图中 ∠A的对边记作a ∠B的对边记作b ∠C的对边记作c
注意
▪ sinA是一个完整的符号，它表示∠A的正弦， 记号里习惯省去角的符号“∠”；
▪ sinA没有单位，它表示一个比值，即直角 三角形中∠A的对边与斜边的比；
，
则sin∠A=___.
b3
5、如图，在△ABC中， AB=CB=5， sinA= ，求△ABC 的面积.
4 5
B
5
5
A
C
如图，在Rt△ABC中，∠C＝90°，
我们把锐角A的邻边与斜边的比叫做∠A的
余弦（cosine），记作cosA， 即

n 比值 AB
n 比值
AC 叫做∠α的余弦，记做cosα
AB
BC 叫做∠α的正切 ，记做tanα
AC
B
α
AC
sin BC cos AC tan BC
AB
AB
AC
锐角α的正弦、余弦、正切 统称为∠α的三角函数
•sin如图 B，ACB在Rts⊿inAABC中A，斜的边 ∠对C边=Rt∠ A
cos AC
3 3 ，13
13
13
2 2 13
13
13 ，
3
y P (2,3)
α
O
x
M
2
w1.如图,在Rt△ABC中,锐角A的对边和邻边同时
扩大100倍,tanA的值（ ）
B
wA.扩大100倍 B.缩小100倍
wC.不变
D.不能确定
w2.已知∠A,∠B为锐角
A
┌ C
w(1)若∠A=∠B,则tanA tanB;
sinA= 3
B
5
D
C
A
２、如图，在△ABC中，D若AB=5，BC=3，则下列 结论正确的是（ ）
A．sinA=
4
5
3
B．sinA=
5
3
C．sinA=
D.以上结论都不正确
4
3、如图，在Rt△ABC中，∠ACB=90°，作CD⊥AB于D，
若BD=2，BC=3．则sinA=
.
2
3
A
５ A
B 3 C
C 3 B
体验到一种学习方法：猜想 证明 归纳 应用
∠α的正弦 ∠α的余弦 ∠α的正切
书面作业： 教科书P6中的作业题。(必做题)

• 10、人的志向通常和他们的能力成正比例。2021/1/142021/1/142021/1/141/14/2021 6:41:13 PM • 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/1/142021/1/142021/1/14Jan-2114-Jan-21 • 12、越是无能的人，越喜欢挑剔别人的错儿。2021/1/142021/1/142021/1/14Thursday, January 14, 2021 • 13、志不立，天下无可成之事。2021/1/142021/1/142021/1/142021/1/141/14/2021
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
边之比 定义 表示 公式
B
∠A的对边a 正弦函数
斜边c
∠A的
对边 ∠A的邻边b
a
斜边c
余弦函数
sinA cosA
sssiiinnn
AAA
===
aaa ccc
cccooosss
AAA
===
bbb ccc
A
∠ A的邻边b
C
∠A的对边a ∠A的邻边b
正切函数

w 看图说话: w 直角三角形三边的关系. w 直角三角形两锐角的关系. w 直角三角形边与角之间的关系. w 特殊角300,450,600角的三角函数
值.
w 互余两角之间的三角函数关系. w 同角之间的三角函数关系
B
c
a
┌
A
b
C
300 450
450 ┌ 600 ┌
习题
w1.计算;(1)tan450-sin300; w(2)cos600+sin450-tan300;
2
w例2 如图:一个小孩荡秋千,秋千链子的长度
为2.5m,当秋千向两边摆动时,摆角恰好为600, 且两边摆动的角度相同,求它摆至最高位置时与 其摆至最低位置时的高度之差(结果精确到 0.01m).
O
w老师提示: 将实际问 题数学化.
●
2.5
B ┌C D A
例3。一位同学的手臂长65cm，当他高 举双臂时，指尖高出头顶35cm。问当他 的手臂与水平成角60度时，指尖高出头 顶多少cm（精确到0。1cm）？
1.1锐角三角函数（2）
n 300,450,600角的三角函数值
脑中有“图”，心中有
锐角三角函数“定式”义
w直角三角形中边与角的关系:锐角三角函数.
w在直角三角形中,若一个锐角确定,那么这个角的对边,
邻边和斜边之间的比值也随之确定.
sin A a , cos A b ,
c
c
B
sin B b , c
3 6 ta 2 3 0 n 0 3 s6 i0 n 0 2 c4 o 0 .5 s
w2.如图,河岸AD,BC互相平行,桥AB 垂直于两岸.桥长12m,在C处看桥两端 A,B,夹角∠BCA=600. w求B,C间的距离(结果精确到1m).

？ 求BE的长．
B(山顶）
H
当锐角为30°时，
30°
西坡
其所对的直角边与
斜边之比始终
30°
A
D
B(山顶）
为 1．
C
2
E
东坡
当锐角为45°时，
其所对的直角边
30°
CF
D
B(山顶）
与 斜边之比始 终为 2 ．
2
当锐角为50°时，
G 南坡
这个比值是一个确 定的值．
C
HD
任意作一个锐角∠A，在角的边上任意取两点B
与B1分别作BC⊥AC于点C ，B1C1⊥A1C1于点C1.
判断 BC 与 B1C1 是否相等，并说明理由. B１
AB
AB1
B
A
C C１
对于每一个确定的锐角α，在角的边上任意取
一点B作BC⊥AC于点C，比值 BC 是一个确
定的值．
AB
B
A
C
直角三角形中锐角ɑ与其对边与斜边比值关系
ɑ
BC （对边与斜边比值）
1.1锐角三角函数（1）
我关心的是本质 其它都是细节（爱因斯坦）
一 情境创小设红、小强、小颖约好去爬山，他们沿不同倾 斜度的三条道路上山，若山顶与山下的铅垂距离为100 米，你能分别求出他们到达山顶要走的路程吗？
南坡
50°
小颖出发地
西坡
东坡
30°
小红出发地
45°
小强出发地
转化成的数学问题 B(山顶）
2.sinα是一个完整的符号，单独的“sin”没有意义.
练一练
1. 如图△ABC中，∠C=90°,BC=5,AC=12B.
5
计算：（1）sinA= 13.

观察归纳
1、了解三角函数的概念； 2、会用符号表示一个锐角的三种三角函数； 3、掌握在直角三角形中，锐角三角函数与边之比的关系；
4、会根据锐角三角函数的定义求锐角三角函数。
sin读音 cos读音 tan读音源自结 论这里邻边指的都是直角边.
探究1
探究2
探究3
在RtΔABC中，如果各边长度都扩大为原来
1.1 锐角三角函数
——第1课时
自学指导
结合思考题自学P（4）--（5）课内练习前内容，并完
成课内练习
显示练习（点我）
思考下面问题： 1、sinα、cos、tanα 分别代表什么意义，这个α有什么要求？ 2、sinα、cos、tanα 的范围分别是什么？ 3、sinα、cos、tanα 是不是函数，为什么？
的2倍，则锐角A的正切值（ D ）
（A）扩大2倍 （B）缩小2倍
（C）扩大4倍
（D）没有变化
返回（点我）

观察以上计算结果,你发现了什么?
sinA=cosB ，cosA=sinB (∠A+∠B=90）
tanA·tanB=1
(∠A+∠B=90）
B
c
a
┌
A
b
C
sin A a cos A b tan A a
c
c
b
sin B b cos B a
c
c
tan B b a
如图，在△ABC中，若AB=5，BC=3，则下列结论正确
锐角A，A′的余弦值的关系为（ ） A
A．cosA=cosA′ B．cosA=3cosA′ C．3cosA=cosA′ D．不能确定 2．如图，已知P是射线OB上的任意一点，PM⊥OA于M，
且PM：OM=3：4，则cosα的值等于（ C）
3 A．4
4 B．3
C．4 5
3
D．
5
3．在△ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a，
是关于锐角α的三角函数。
AB AB AC
B
A
C
锐角α的正弦，余弦和正切统称∠α的三角函数.
比值 BC 叫做∠α的正弦(sine)，记做sinα.
AB
BC
比值 AC
即sinα= AB
叫做∠α的余弦(cosine) ，记做cosα.
AB
即cosα= AC
AB 比值 叫做∠α的正切(tangent) ，记做tanα.
b，c，则下列各项中正确的是（ ） B
A．a=c·sinB B．a=c·cosB C．a=c·tanB D．以上均不正确
4．在Rt△ABC中，∠C=90°，cosA= 2 ，则tanB等于（ ）
C

想一想
B
B1
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
BC
B 1C 1 A C
AC1 BC
(2) A B 和 A B 1 , A B 和A B 1 , A C
和B
A
1C C
1 1
有什么关系?
A
(3)如果改变B在梯子上的位置
呢?
C C1
动手实践，寻找规律 • 由推理可得：角度不变，比值不变 • 由动态演示：动手实践，寻找规律 • 由推理可得：角度不变，比值不变 • 由动态演示：角度改变，比值改变
5.如图, ∠C=90°CD⊥AB.
()()()
sin B .
()()()
A
C
┌ DB
6.在上图中,若BD=6,CD=12.求cosA的值.
w7.如图,分别根据图(1) 和图(2)求∠A的三个三角 函数值.
w8.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求sinA和cosB (2)BC=3,sinA= 5 ,求AC和AB.
5 sinB= 4
5 B
4 cosA= 5 cosB= 3
5
3 tanA=
4 tanB= 4
3
观察以上计算结果,你发现了什么?
若AC=5,BC=3呢? C
变变
• 在Rt⊿ABC中，∠C=Rt∠， 求锐角∠A的余弦
sinA= 3 5
B
A
C
变变变
在Rt⊿ABC中，∠C=Rt∠， sinA CD⊥AB，求锐角∠DCB的余弦
=
3 5
B D
C
A
例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.

当堂检测
7.在Rt△ABC中,∠C=90°, AB=15,tanA=3,求AC和BC.
4
∴设BC=3k,AC=4k.
15
A
4k
B
3k
┌ C
课堂小结
【正切的定义】 如图，在Rt△ABC中，∠C=90°， 我们把∠A的对边a与邻边b的比，叫做∠A的正切，
记作tanA，tanA
=
∠A的对边 ∠A的邻边
正切。 3.坡度越大,坡面越陡。
讲授新课
知识归纳
【坡度的定义】 通常把坡面的垂直高度h与水平方向的距离l的比叫做坡度（或叫做坡比）， 坡度越大，坡越陡
讲授新课
典例精析
【例2】如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B 到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).
AC2
AC1
B2C2 , AC2
B1 B2 B3
C3 C2
C1
（3）如果改变B2在梯子上的位置（如B3）呢？ 比值不变
（4）由此你能得出什么结论？ 直角三角形中，锐角大小确定后，对 应的对边和邻边的比值也就确定了
讲授新课
归纳：
由此可得，在有一个锐角相等的所有直角三角形中，这个锐角的对边
与邻边的比值是一个常数，与直角三角形的大小无关.
数学（浙教版）
九年级 下册
第1章 解直角三角形
1.1 锐角三角函数 第1课时 正切
学习目标
1. 理解正切的意义和与现实生活的联系； 2.能够用表示直角三角形中两直角边的比，表示生活中物体的倾 斜程度、坡度（坡比）等； 3.能够根据直角三角形的边角关系，用正切进行简单的计算；
温故知新
对直角三角形的边角关系，已经研究了什么？还可以研究 什么？

及其三角函数 求另一边
求另一边
sin A a , c
acsin A. c a . sin A
B
ca ┌
A bC
cos A b , c
bccoA.s c b . cos A
A
tan A a , b
abtaA n. b a . tan A
α β┌
w 2模型: A D ta9n00 ata9n00 . B a C
Bα
β
C
A
w9 如图,根据图中
已知数据,求AD.
α β┌ Ba C D
探索下列关系式是否成立（00〈α〈900）？
（1） sinα+cos α≤1 （2） sin2α= 2sinα
P16 习题1.4 1,2题
w1.用计算器求下列各式的值： w(1)tan320;(2)sin24.530; w(3)sin62011′;(4)tan39039′39 ″w2..如图,物华大厦离小伟家60m,小伟 从自家的窗中眺望大厦,并测得大厦顶 部仰角是450,而大厦底部的俯角是370, 求该大厦的的高度 (结果精确到0.1m).
• 10、人的志向通常和他们的能力成正比例。2020/12/192020/12/192020/12/1912/19/2020 11:30:37 AM • 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2020/12/192020/12/192020/12/19Dec-2019-Dec-20 • 12、越是无能的人，越喜欢挑剔别人的错儿。2020/12/192020/12/192020/12/19Saturday, December 19, 2020 • 13、志不立，天下无可成之事。2020/12/192020/12/192020/12/192020/12/1912/19/2020