幅角原理
- 格式：doc
- 大小：403.50 KB
- 文档页数：5
下载文档原格式
合集下载
自动控制原理 第五章(第四和五次)
6
5-5 频域稳定判据（奈氏判据）
自动控制原理
G(s)H(s)
K
(10s 1)(2s 1)(0.2s 1)
Im
K=100
P=0; R=-2;
Z=0-(-2)=2 闭环系统在 s 右半平面有两个 极点，系统不稳定
-1
+∞
ω=0
Re
闭环传递函数在复平面右半平面有Z个极点
Z PR
R(>0)为Nyquist曲线逆时针包围（-1，j0）点的圈数; R(<0)为Nyquist曲线顺时针包围（-1，j0）点的圈数;
➢只要在这个闭合曲线 内没有F(s)的零点，系 统即为稳定的。
+∞ Im ∞
O Re
-∞
3
5-5 频域稳定判据（奈氏判据）
自动控制原理
➢对于真有理分式，s等于无穷
大的时候，|G(s)H(s)|=0，在
+∞ Im
G(s)H(s)曲线中对应坐标原点。
∞
➢我们只需考察S在虚轴上取值
O
的情况
Re
➢ s j 在复平面上的
自动控制原理
(2)开环传递函数含ν 个积分环节 ν型系统
Ga (S )
K S (TS 1)
Im
-1
0
(a)ν=1,从 0 点逆时针
0 Re
补画半径为无穷大的1/4圆。
0
P=0, N=0，Z=0，
所以，闭环系统稳定。
22
5-5 频域稳定判据（奈氏判据）
自动控制原理
Im
0 -1 0
＝0
曲线G，( j就)是HN( jyq)uist曲线
-∞
4
5-5 频域稳定判据（奈氏判据）
机械工程控制基础 第五章
第五章简介：本章介绍了单输入单输出控制系统稳定性的定义及其判定依据。
对于不同的系统，稳定性的定义不同。
系统的稳定性指标是控制系统设计过程中需要考虑的众多性能指标中最重要的指标,不稳定的系统是无法使用的。
主要包括赫尔维茨判据、劳斯判据、幅角原理、奈奎斯特稳定性判据等概念.重点是赫尔维茨稳定性判据和劳斯稳定性判据及其在系统分析中的应用.难点是应用复变函数的幅角原理推导奈奎斯特稳定性判据和对稳定裕度的理解。
随堂测试：一、知识点名称1：控制系统稳定性的基本概念1。
是保证控制系统正常工作的先决条件。
（）A．稳定性B．快速性C．准确性D．连续性正确答案：A解析：不稳定的系统是无法使用的。
2。
是控制系统最重要的性能指标。
（）A．稳定性B．快速性C．准确性D．连续性正确答案:A解析：稳定性是控制系统最重要的性能指标知识点名称2：单输入单输出控制系统稳定的条件1.单输入单输出控制系统稳定的条件为(）A 特征方程根具有副实部B特征方程根具有副实部C极点位于复平面的右半部D极点位于虚轴上正确答案:A解析：单输入单输出控制系统稳定的充分必要条件为特征方程根全部具有副实部2。
某单位反馈系统的开环传递函数为,则该系统稳定的K值范围为（) A.K〉0 B。
K>1 C。
0〈K<10 D K〉-1正确答案:A解析:其特征方程为,根据二阶螺丝准则和朱里准则，该系统稳定条件为;所以的K的取值范围为K〉0知识点名称3：赫尔维茨稳定性判据1。
赫尔维茨矩阵的各项主子式行列式的值全部为正,是线性系统稳定的条件。
(）A.充分 B 必要C充要 D 即不充分也不必要正确答案:C解析：线性系统稳定的充要条件赫尔维茨矩阵的各项主子式行列式的值全部为正。
2。
如果满足主子式前提下，若所有次顺序赫尔维茨矩阵的主子式为正，则所有次顺序赫尔维茨矩阵的主子式为正。
（）A BC D正确答案：B解析：如果满足条件,若所有奇次顺序赫尔维茨矩阵的主子式为正，则所有偶次顺序赫尔维茨矩阵的主子式必为正；反之亦然。
自动控制原理第五章-2
截止频率c ：开环幅相曲线上，幅值为1的频率称为截止频率。 即 |G(jwc)H(jwc)|=1。 相角裕量 ： 物理意义：若系统截止频率c处的相位迟后再增加，系统处于临界 = 180 + (c)
稳定。
Im
1 Kg
wg
Re
(wc )
wc
w
开环对数幅相曲线上的幅值裕度和相角裕度
-Kg(dB)
Kg(dB)>0
K g (dB) 20 lg
1 20 lg G ( jwg ) H ( jwg ) G ( jwg ) H ( jwg )
若系统稳定，则：Kg>1(K(dB)>0)，r>0。 一般，为确定系统的相对稳定性，描述系统的稳定程度， 需要同时给出幅值裕度和相位裕度两个量，缺一不可。 工程上，一般取：
1 T w 1
2 2
(w) arctanTw
M (0) 1, M r 1, wr 0, wb 1/ T ts 3T 3 / wb , tr 2.20T 2.20 / wb
( 0.05)
T 2
2、二阶系统 R(s)
_
2 wn s( s 2wn )
K g (dB) 10dB r 300 ~ 600
(K g (dB) 6dB)
判断系统稳定的又一方法
0
h(dB) 0
h 1
180 G( jc )H ( jc )
h 20 log G ( j g ) H ( j g )
1 h G( j g ) H ( j g )
2. 带宽频率b
当系统闭环幅频特性的幅值M()降到零频率幅值的0.707(或零分贝值以下3dB) 时，对应的频率b称为截止频率。0～b的频率范围称为带宽，它反映系统的快速 性和低通滤波特性。
稳定。
Im
1 Kg
wg
Re
(wc )
wc
w
开环对数幅相曲线上的幅值裕度和相角裕度
-Kg(dB)
Kg(dB)>0
K g (dB) 20 lg
1 20 lg G ( jwg ) H ( jwg ) G ( jwg ) H ( jwg )
若系统稳定，则：Kg>1(K(dB)>0)，r>0。 一般，为确定系统的相对稳定性，描述系统的稳定程度， 需要同时给出幅值裕度和相位裕度两个量，缺一不可。 工程上，一般取：
1 T w 1
2 2
(w) arctanTw
M (0) 1, M r 1, wr 0, wb 1/ T ts 3T 3 / wb , tr 2.20T 2.20 / wb
( 0.05)
T 2
2、二阶系统 R(s)
_
2 wn s( s 2wn )
K g (dB) 10dB r 300 ~ 600
(K g (dB) 6dB)
判断系统稳定的又一方法
0
h(dB) 0
h 1
180 G( jc )H ( jc )
h 20 log G ( j g ) H ( j g )
1 h G( j g ) H ( j g )
2. 带宽频率b
当系统闭环幅频特性的幅值M()降到零频率幅值的0.707(或零分贝值以下3dB) 时，对应的频率b称为截止频率。0～b的频率范围称为带宽，它反映系统的快速 性和低通滤波特性。
幅角基本知识及其应用
f (z) z a g(z)
g(z)
由此，a为 f '(z) 一阶极点且Res[ f '(z) ，a] = n。
f (z)
f (z)
4
引例2 设b为f (z)的m阶零点，证明：b 为 f '(z) 一阶极点
f (z) 且Res[ f '(z) ，a] = -m。
f (z)
证明 b为f(z)的m级极点，则在b的去心邻域内有
2 i
d ln
C
f (z)
1
2 i
[ dln
C
|
f
(z)
| i d arg
C
f
(z)]
C arg f (z)
2
7
二、幅角原理
定理2 设C一条周线，f(z)符合条件：1 f(z)在C内是亚纯的； 2 f(z)在C上解析且不为零，则有
N( f ,C) P( f ,C) C arg f (z)
零点数为： N f ,C 3
6
定理1 设C一条周线，f(z)符合条件：1 f(z)在C内是亚纯的； 2 f(z)在C上解析且不为零，则有
另一dz f (z)
N( f ,C) P(
f ,C)
1
2 i
C
f '(z) dz f (z)
1
2 i
d
C
dz
[lnf
(
z)]dz
1
arg P iy n
y( )
9
10
三、儒歇（Rouché）定理
z在C上时有：(z) f (z)
11
儒歇定理
(z) f (z)
注：儒歇定理的 典型用途之一是将一个复杂的解析函数g同
幅角定理的数学原理及应用
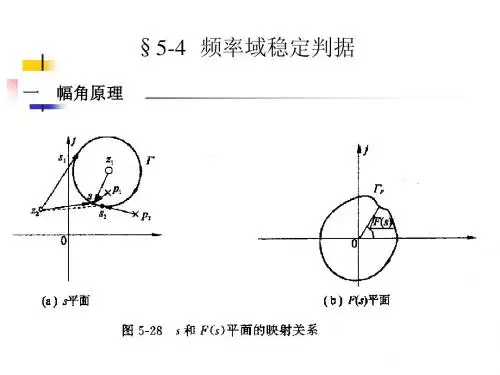
幅角定理的数学原理及应用一、幅角定理的数学原理幅角定理是数学中与复数相关的重要定理，它描述了复数的乘法运算中幅角的变化规律。
幅角定理的具体表述如下：在复数相乘时，幅角相加。
1.1 复数的表示在讨论幅角定理之前，我们首先需要了解复数的表示方法。
一般情况下，复数写作 a + bi 的形式，其中 a 和 b 分别表示复数的实部和虚部，i 是虚数单位。
1.2 幅角的定义在复平面上，以复数所在点与实轴的正半轴之间的角度为幅角，记作arg(z)。
幅角一般取值为 [-π, π]，即范围为半开区间。
1.3 幅角定理的表述幅角定理指出，当两个复数相乘时，它们的幅角相加。
具体地，设复数 z1 和z2 分别表示为 z1 = a + bi 和 z2 = c + di，则它们的乘积 z = z1 * z2 的幅角为arg(z) = arg(z1) + arg(z2)。
二、幅角定理的应用幅角定理在数学以及工程学科中具有广泛的应用，下面我们将介绍几个常见的应用场景。
2.1 信号处理在信号处理领域中，幅角定理被广泛应用于对信号的频谱分析。
对于一个复数序列，我们可以将它映射到复平面上，然后计算每个复数的幅角。
通过对幅角进行进一步的处理，我们可以得到信号的相位谱。
2.2 电路分析幅角定理在电路分析中也有重要的应用。
当电路中存在多个元件连接时，我们可以将每个元件的阻抗或电导映射为复数，并使用幅角定理计算整个电路的幅角。
这可以帮助工程师分析电路的相位特性，从而设计出更好的电路。
2.3 控制系统在控制系统中，幅角定理被用于稳定性分析和控制器设计。
通过将控制系统中的传递函数表示为复数形式，并利用幅角定理计算系统的相位裕度，可以判断系统是否稳定。
此外，幅角定理还可以帮助工程师设计合适的控制器来调节系统的相位响应。
2.4 图像处理在图像处理领域中，幅角定理被用于图像的频域分析。
通过将图像转换为频域信号，我们可以计算每个频率分量的幅角。
这有助于识别图像中的边缘和纹理等特征，并用于图像增强、图像压缩和图像识别等应用。
复变函数-幅角原理及其应用
f (z) z a g(z)
g(z)
由此，a为 f '(z) 一阶极点且Res[ f '(z) ，a] = n。
f (z)
f (z)
4
引例2 设b为f (z)的m阶零点，证明：b 为 f '(z) 一阶极点
f (z) 且Res[ f '(z) ，a] = -m。
f (z)
证明 b为f(z)的m级极点，则在b的去心邻域内有
零点数为： N f ,C 3
6
定理1 设C一条周线，f(z)符合条件：1 f(z)在C内是亚纯的； 2 f(z)在C上解析且不为零，则有
另一方面
1
2 i
C
f '(z) dz f (z)
N( f ,C) P(
f ,C)
1
2 i
C
f '(z) dz f (z)
1
2 i
dCdz来自[lnf(z)]dz
1
arg P iy n
y( Z )
9
10
三、儒歇（Rouché）定理
z在C上时有：(z) f (z)
11
儒歇定理
(z) f (z)
注：儒歇定理的 典型用途之一是将一个复杂的解析函数g同
零点已知的解析函数比较，推出关于零点的一些信息。
例4 证明多项式 g(z) z4 3z+1 的全部4个零点都位 于 z 2 内。 例5 证明: 满足条件 at | a0 | | a1 | L | at1 | | at1 | | an|
4
8
在自动控制中，一些技术的稳定性归结为要求常系 数线性微分方程解的稳定性，而这类问题要求该方 程的特征多项式
P z a0zn a1zn1 L an
复变函数--幅角原理
§3 辐角原理及其应用一、教学目标或要求：掌握幅角原理的准确叙述及其应用二、教学内容（包括基本内容、重点、难点）： 基本内容：对数留数 幅角原理 例题 重点：幅角原理 例题 难点: 幅角原理 例题 三、教学手段与方法： 讲授、练习思考题、讨论题、作业与练习： 11－14§3 辐角原理及其应用1．对数留数留数定理的另一个应用的考虑形如 的复变函数在极点处的留数,以之导出辐角原理,提供确定解析函数零点个数的一个有效工具。
积分dzz f z f i C ⎰)()('21π称为)(z f 的对数留数。
引理 6.4（1）设为的级零点，则必为的一级极点，且 ；（2）设为的级极点，则必为的一级极点，且 。
证 （1）若设为的级零点，则在的邻域内，，其中在的邻域内解析,且,于是, 从而。
由于在是邻域内解析,故可在的邻域内展开成Taylor级数,必定不含的负幂项，因此必为的一级极点，且。
（2）设为的级极点，则必为的级零点，由（1）的结论,必为的一级极点，且。
定理6.9设为一条围线，满足条件：（1）在的内部除可能有极点外是解析的；（2）在上解析且不为零，则，其中与分别表示在内部的零点与极点的个数(一个级零点算作个零点，一个级极点算作个极点)。
证由第五章(二)习题14知,在内部至多只有有限个零点和极点。
设为在内部的不同零点，其级相应地为,为在内部的不同极点,其级相应为。
根据引理 6.4，、都是的一级极点，于是，在内部及上除去、，外均解析，故由留数定理2. 辐角原理辐角原理 在定理6.9的条件下，函数)(z f 在C 内部的零点个数与极点个数之差，等于当z 沿C 之正向绕行一周后的改变量)(arg z f C ∆除以π2，即π2)(arg ),(),(z f C f P C f N C ∆=- (6.27)特别地，如果在围线C 上及C 之内部均解析，且在C 上不为零，则π2)(arg ),(z f C f N C ∆=(6.28)证（大意）根据定理6.9，注 定理6.9（2）可减弱为“连续到边界,且沿,”，围线也可以是复围线。
自控原理中的幅角原理
在自控系统中，幅角原理表明当反馈增益大于零且相位差小于180度时，系统将保持稳定。也就是说，负反馈将输出信号的相位差控制在相对较小的范围内，并且维持一个合适的幅度。
为了更好地理解幅角原理，我们可以以一个简单的例子来说明。假设我们有一个加法器，它的输入信号是两个正弦波，一个具有幅度A和相位差为0度，另一个具有幅度B和相位差为180度。输出信号的幅度和相位差如何取决于输入信号的幅度和相位差呢？
幅角原理在电子电路设计和信号处理中具有重要的应用。通过调整幅度和相位差，可以优化系统的性能和稳定性。在自动控制系统中，幅角原理是保持系统稳定的关键原则之一。
总结起来，幅角原理指出当反馈增益大于零且相位差小于180度时，系统将保持稳定。通过控制幅度和相位差，可以优化自控系统的性能。幅角原理在自动控制、电子电路设计和信号处理等领域中具有重要意义。
自控原理中的幅角原理
自控原理中的幅角原理是指当系统通过负反馈进行调节时，系统的稳定性取决于系统的幅度和相位的特性。在稳定的自控系统中，系统的稳定性可以通过幅度和相位的特性来衡量。
首先，我们先来了解什么是幅度和相位。在频率域中，幅度是指输入信号和输出信号之间的幅值的比值，通常用dB来表示。相位是指输出信号的相位与输入信号之间的差值，通常用角度来表示。
假设相位差为180度，即φ= -180度。这意味着输出信号的相位与输入信号的相位差为180度。在这种情况下，输出信号将随时间变化，系统无法达到稳定状态。
因此，幅角原理告诉我们，系统的稳定性取决于输入信号的幅度和相位。当反馈增益大于零时，反馈信号能够减小系统的幅度差和相位差，从而使系统保持稳定。只有当幅度差小于零且相位差小于180度时，系统才能有效地进行调节。
我们知道加法器的输出信号等于两个输入信号的和。因此，输出信号的幅度将是两个输入信号幅度之和：A + B。相位差取决于两个输入信号的相位之间的差值：φ= 0 - 180 = -180度。
为了更好地理解幅角原理，我们可以以一个简单的例子来说明。假设我们有一个加法器，它的输入信号是两个正弦波，一个具有幅度A和相位差为0度，另一个具有幅度B和相位差为180度。输出信号的幅度和相位差如何取决于输入信号的幅度和相位差呢？
幅角原理在电子电路设计和信号处理中具有重要的应用。通过调整幅度和相位差，可以优化系统的性能和稳定性。在自动控制系统中，幅角原理是保持系统稳定的关键原则之一。
总结起来，幅角原理指出当反馈增益大于零且相位差小于180度时，系统将保持稳定。通过控制幅度和相位差，可以优化自控系统的性能。幅角原理在自动控制、电子电路设计和信号处理等领域中具有重要意义。
自控原理中的幅角原理
自控原理中的幅角原理是指当系统通过负反馈进行调节时，系统的稳定性取决于系统的幅度和相位的特性。在稳定的自控系统中，系统的稳定性可以通过幅度和相位的特性来衡量。
首先，我们先来了解什么是幅度和相位。在频率域中，幅度是指输入信号和输出信号之间的幅值的比值，通常用dB来表示。相位是指输出信号的相位与输入信号之间的差值，通常用角度来表示。
假设相位差为180度，即φ= -180度。这意味着输出信号的相位与输入信号的相位差为180度。在这种情况下，输出信号将随时间变化，系统无法达到稳定状态。
因此，幅角原理告诉我们，系统的稳定性取决于输入信号的幅度和相位。当反馈增益大于零时，反馈信号能够减小系统的幅度差和相位差，从而使系统保持稳定。只有当幅度差小于零且相位差小于180度时，系统才能有效地进行调节。
我们知道加法器的输出信号等于两个输入信号的和。因此，输出信号的幅度将是两个输入信号幅度之和：A + B。相位差取决于两个输入信号的相位之间的差值：φ= 0 - 180 = -180度。
自动控制理论之频率域稳定判据及稳定裕度探讨讲诉
图5－47绘出了K>1 和 K<1的两条闭合曲线，可见：
当K>1 时，曲线逆时针包围了（－1，j0）点1圈即R=1 闭环系统稳定；当K<1时，曲线未包围（－1，j0）点，即 R=0，闭环系统不稳定。
在本例中，K值大才能使系统稳定，K值小反而使闭环系 统不稳定，这是与常见的最小相位系统截然不同之处。
因此，我们可以看出，辅助函数具有如下特征：
1）辅助函数F(S)是闭环特征多项式与开环特征多项式 之比，故其零点和极点分别为闭环极点和开环极点。
2）因为开环传递函数分母多项式的阶次一般大于或等 于分子多项式的阶次，故F(S)零点、极点的个数相同，均 为n个。
3）F(S)与开环传递函数G(S)H(S)之间只差常量1。 F(S)=1+G(S)H(S)的几何意义为：F平面上的坐标原点就是 GH平面上的（－1，j0）点，如图5-42所示。
负实数，即S平面右半部分无开环极点，P=0。频率特性及
其镜像组成的封闭曲线如图5－44右所示。可见，当ω 从 －∞→＋∞ 时，闭合曲线并未包围（－1，j0）点，故N＝ 0。因此闭环系统总是稳定的。我们也可以利用劳斯判据 进行判定。
例5-8 设系统开环传递函数为
5.2 G(s)H (s) (s 2)(s2 2s 5)
图5-45 例5-8系统的极坐标图及其镜像
例5-9 系统结构图如图5-46所示，试判断系统的稳定性并 讨论K值对闭环系统稳定性的影响。
图5-46 解：图示系统是一个开环不稳定系统，其开环传递函数在 S平面右半部分有一个极点P＝1，频率特性曲线如图5－ 47所示。当ω ＝0时，曲线从负实轴（－K，j0）出发；当 ω→∞时，曲线以－90°渐近角趋于坐标原点；当ω从－∞ 变化到＋∞，频率特性（图中实线部分）及其镜像（虚线 部分）包围（－1，j0）点的圈数R与K值有关。
复变函数之幅角原理
+
z
m −a
,
ϕ ′( z ) ϕ(z)
=a0
+
a1 ( z
−
a) +
a2 ( z
−
a)2
+ ，(没有负幂项)
，代入
f ′(z) 的等式得
f (z)
a是
f ′(z)的一级极点,且
f (z)
Res
f ′(z) ,
f (z)
a
=a−1
=
m.
定理1(P125) 设a是f (z) 的m 级零点, b是f (z) 的n 级极点，
2π i
C
f f
′(= z) d z n (z) =k
m
αk +
1=j 1
-β =j
N − P.
(C的内部为D, D 内去掉f (z)的全部有限极点外为D1.)
定理2(P126) 设f (z)在闭路 (正向) C 的内部可能有有限个极点，
除去这些极点外,f (z)在C及其内部解析，且f (z)在C上无零点，
( f 在C内最多只有有限个极点,肯定没本性奇点) (∀z ∈ C, f ( z) ≠ 0)
则
1
2π
i
∫C
f ′(z) d=z f (z)
N − P,
N 表示f (z)在C 内零点总数,
(每一个k级零点算成k个零点)，
P表示f (z)在C内的极点总数 (每一个k级极点算成k个极点) .
证明 由条件知 f (z)在C上解析且无零点,故 f'(z) 在C上解析.
(z)
, ak
.
故先求 f ′(z) 在C内所有奇点，即f (z)的所有奇点和零点，并求它们的留数. f (z)
范后宏教授报告--复数,多值函数,辐角原理
7)L.Euler 引进 i = √ −1
√ −1
−1 sin θ)α = cos αθ +
−1 sin αθ . 计
算了
,但计算的答案不全. 现在正确的答案是：
√ −1
√
−1
= {e−(2k+ 2 )π |k 取所有整数} (多 值 ！)
1
√ − − → 8)C.Wessel 1789年用向量运算表示虚数运算 a + b −1 = 向量OP √ 9)J.Argand 用极坐标表示虚数 a + b −1 = r(cos θ + i sin θ) √ 10)C.F.Gauss 用平面中的几何点来表示虚数 a + b −1 .(图略) 意义：几何表示表明虚数运算不可能推出来矛盾，因此虚数的存在是合法的，不再是“虚”
sechz ≡
6
(26)
双曲余割函数 1 . shz
cschz ≡
(27)
反正弦 √ z 2 − 1)).
Arcsinz ≡ −iLn(i(z +
(28)
பைடு நூலகம்
反余弦 √
Arccosz ≡ −iLn(z +
z 2 − 1).
(29)
反正切 i i+z Ln . 2 i−z
Arctanz ≡
(30)
反余切 i z−i Ln . 2 z+i
4)Issac Newton 误认为虚数根没有物理、几何含义. √ −1 介于存在于不存在之间的两栖物. √ −1 sin θ)n = cos nθ + √ √ −1 sin nθ.
5)G.W.Leibniz 1762年认为虚数
6)A.De Moivre 在1707 1730年逐步计算出虚数的整数幂. (cos θ + √ −1 符号，计算虚数的实数指 数 (cos θ + √
辐角的原理及应用
辐角的原理及应用什么是辐角辐角也被称为幅角，是指向量与参考轴之间的角度。
在数学中，辐角常用于描述复数的相位，表示复数与实轴之间的夹角。
辐角的原理辐角的计算可以使用三角函数来进行。
以复数z=a+bi为例，其中a为实部，b 为虚部。
我们可以使用反正切函数来计算辐角，公式如下：arg(z) = atan(b/a)其中，atan为反正切函数，b/a表示复数的虚部与实部之比。
辐角的计算结果为弧度制。
在计算机中，通常使用math库中的atan2函数来计算辐角，该函数可以处理实部为0的情况。
辐角的应用辐角在各个领域有着广泛的应用，以下是一些常见的应用场景：1. 电工学在电工学中，辐角用于描述交流电的相位差。
交流电的正弦波可以表示为A*sin(ωt+φ)，其中A为电流的幅值，ω为频率，t为时间，φ为辐角。
辐角决定了交流电的相位，从而影响电压、电流的波形以及电路的特性。
2. 信号处理在信号处理中，辐角用于描述频谱中不同频率成分的相位差。
相位差反映了不同频率成分之间的时间延迟关系，是分析和合成信号的重要参数之一。
辐角的变化可以反映信号的频率变化情况。
3. 几何学在几何学中，辐角可以用于描述向量之间的夹角。
例如，两个向量的辐角为0度时，表示它们方向相同；辐角为90度时，表示它们相互垂直。
4. 复数运算辐角在复数运算中有着重要的作用。
复数乘法中，两个复数的辐角相加，模长相乘，可以得到乘积的辐角。
复数的辐角也可以用于求解复数的幅值和幂运算。
5. 控制系统在控制系统中，辐角可以用于描述系统的相位相位辐角将直接影响系统的稳定性和性能。
通过对辐角进行调整，可以实现控制系统对信号的滤波、补偿和调节。
总结辐角作为描述向量相对于参考轴的角度，具有广泛的应用。
它在电工学、信号处理、几何学、复数运算和控制系统等领域中起着重要的作用。
了解辐角的原理和应用，有助于深入理解这个概念，并能应用于实际问题的解决。
幅角原理及其应用
1 f '( z ) 1 d 1 dz [lnf ( z )]dz d ln f ( z ) 2 i C f ( z ) 2 i C dz 2 i C 1 [ dln | f ( z ) | i d arg f ( z )] 2 i C C C arg f ( z ) 2
例3 证明：在虚轴上没有零点的n次多项式
P z a0 z n a1z n1 an （a0 0）
y (
arg P iy n
)
9
10
三、儒歇（Rouché ）定理
z在C上时有： ( z ) f ( z )
11
儒歇定理
( z ) f ( z )
幅角原理及应用
1
留数和留数定理
一、对数留数
二、 幅角原理 三、儒歇定理
2
留数和留数定理
定义：如果函数 f 在区域D内除去极点外 处处解析，则称f 为区域D内的亚纯函数。
有理函数在整个平面上都是亚纯ቤተ መጻሕፍቲ ባይዱ数 若f 在闭周线C内是亚纯的，在C上解析且不取 零点，则 f 在C内至多有有限个极点。
3
f '( z ) 引例1 设a 为f ( z )的n阶零点，证明：a为 一阶极点 f (z) f '( z ) 且Res[ ，a] = n。 f (z)
5
考察积分
1 f '( z ) dz 2 i C f ( z )
若f ( z)在C内亚纯且在C上解析、不取零值。 f '( z ) 明显地， 的极点只可能来自于f (z)的极点和零点. f (z)
计算函数的零点或极点的个数时，通常包含重数。 2 3 z - 7 z 例1.设 f ( z ) = , 则f ( z )在C： z = 4内的极点数为 4 2 5 z - 5 z + 2 z - 1
自动控制原理--奈奎斯特稳定判据及应用
Ⅱ
F( j)
Ⅲ Ⅰ
F(s)与Gk (s) 的关系图。
11
若奈氏曲线G( jω )H( jω )逆时针包围(−1, j0)点的次数R等于位于右半平面上开环极 点数P。则闭环系统稳定，否则闭环系统不
稳定。
约束条件：在原点和虚轴上无零极点。奈氏轨迹不 能穿过零极点。
讨论：当奈氏曲线通过(−1,j0)点，则表示闭环系 统
。式中， zi , p j
(s pj)
为F(s)的零、极点。
j 1
结论：F(s)的极点为开环传递函数的极点；
F(s)的零点为闭环传递函数的极点；
F(S)平面的坐标原点就是G(S)H(S)平面的
点（-1，0j）
3
F(s)是复变量s的单值有理函数。如果函数F(s)在s平面上指
定的区域内是解析的，则对于此区域内的任何一点 d s都可以在 F(s)平面上找到一个相应的点d f ，d f 称为 ds 在F(s)平面上的映射。
若考虑平面G( jω )H( jω )，则相当于曲线F( jω )左
移一个单位的奈氏图，即开环幅相频率特性，原F平面
原点对应于GH平面(−1, j0)点
G( jω )H( jω ) = F( jω ) −1
∴若要系统稳定，则Z=P−R=0，R为GH 映射曲线绕
(−1,j0)点次数
10
Gk ( j )
P：s平面上被封闭曲线 s 包围的F(S)的极点 Z： s平面上被封闭曲线 s 包围的F(S)的零点 R： F平面上被封闭曲线 f 包围的原点的次数
若R为正，表示 f 逆时针运动，包围原点圈数； 若R为0，表示 f 逆时针运动，不包围原点圈数； 若R为负，表示 f 顺时针运动，包围原点圈数。
6
F( j)
Ⅲ Ⅰ
F(s)与Gk (s) 的关系图。
11
若奈氏曲线G( jω )H( jω )逆时针包围(−1, j0)点的次数R等于位于右半平面上开环极 点数P。则闭环系统稳定，否则闭环系统不
稳定。
约束条件：在原点和虚轴上无零极点。奈氏轨迹不 能穿过零极点。
讨论：当奈氏曲线通过(−1,j0)点，则表示闭环系 统
。式中， zi , p j
(s pj)
为F(s)的零、极点。
j 1
结论：F(s)的极点为开环传递函数的极点；
F(s)的零点为闭环传递函数的极点；
F(S)平面的坐标原点就是G(S)H(S)平面的
点（-1，0j）
3
F(s)是复变量s的单值有理函数。如果函数F(s)在s平面上指
定的区域内是解析的，则对于此区域内的任何一点 d s都可以在 F(s)平面上找到一个相应的点d f ，d f 称为 ds 在F(s)平面上的映射。
若考虑平面G( jω )H( jω )，则相当于曲线F( jω )左
移一个单位的奈氏图，即开环幅相频率特性，原F平面
原点对应于GH平面(−1, j0)点
G( jω )H( jω ) = F( jω ) −1
∴若要系统稳定，则Z=P−R=0，R为GH 映射曲线绕
(−1,j0)点次数
10
Gk ( j )
P：s平面上被封闭曲线 s 包围的F(S)的极点 Z： s平面上被封闭曲线 s 包围的F(S)的零点 R： F平面上被封闭曲线 f 包围的原点的次数
若R为正，表示 f 逆时针运动，包围原点圈数； 若R为0，表示 f 逆时针运动，不包围原点圈数； 若R为负，表示 f 顺时针运动，包围原点圈数。
6
自动控制原理第6章
Z=P–N=0
1 0
Re
0
例4
Gk
s
K
s 2 Ts
1
判断稳定性。
Im
0
0
1 0
Re
P=0
N= -2（2次负穿越）
Z=P–N=2
Gb(s) 有两个极点在右半平面，系统不稳定。
5.4.4 已知开环伯德图时稳定判据 将伯德图转为奈氏曲线再判断。
5.5.1 最小相位系统的稳定裕量
20 lg150 20 lg 2 40 lg10 40 lg 2 20 lg c 20 lg10
20 lg150 20 lg 2 20 lg10 20 lg c
150 10c
2
得
c 30 rad/ s
Gk j
1500.1 j 1 j0.5 j 10.02 j 10.005 j 1
2、由于 f(s )的幅角改变量为 f s 2 P Z ，如果
P Z 0 ，则 f(s ) 一定围绕原点绕行。
我们是要用幅角原理来判断系统的稳定性，即 Gb(s) 极点的分 布情况，而且要用 Gk(s) 来判断，因此一定要涉及Gb(s) 的特征
多项式，不妨设 f s 1 Gk s
特点： 1. f(s ) 的零点是 Gb(s) 的极点，即 1+ Gk(s) 的 Z 是 Gb(s) 的极 点 P ， f(s ) 的 Z 未知。
闭环系统不稳定时的情况：
c
1
1
Im 0, h 1
0 Re
0
Gk ( j1)
Gk ( jc )
当 c 对应的交点在Ⅲ象限时，
Gk jc
0
当 c 对应的交点在Ⅱ象限时，
Gk jc
幅角原理例题讲解
幅角原理例题讲解嘿，朋友们！今天咱来聊聊幅角原理例题讲解。
这玩意儿就像是一把神奇的钥匙，能打开好多复杂问题的大门呢！比如说，有个函数 f(z)，咱要研究它在复平面上的行为。
那幅角原理就派上用场啦！就好像你在迷宫里找路，幅角原理就是那个给你指引方向的小箭头。
咱来看个具体例子哈。
有个函数，它的零点和极点在复平面上分布得乱七八糟的。
这时候，咱就用幅角原理来算算，绕着一个封闭曲线转一圈，函数值的幅角变化了多少。
哎呀，这可有意思了，就像是在数星星，一颗一颗地数清楚。
你想想，要是没有幅角原理，那可不得抓瞎呀！那这些复杂的函数就像一群调皮的小孩子，到处乱跑，咱可管不住。
但有了幅角原理，嘿嘿，它们就得乖乖听话啦。
再打个比方，幅角原理就像是一个厉害的侦探，可以从一些蛛丝马迹中找到问题的关键。
它能告诉我们函数在不同区域的表现，让我们对整个局面有个清楚的了解。
而且哦，学会了幅角原理，你就会发现好多难题都迎刃而解啦！就好像你突然掌握了一门绝世武功，什么难关都不在话下。
举个例子吧，有个复杂的积分，用普通方法算起来那叫一个头疼。
但用幅角原理，说不定一下子就找到突破口啦！这不是很神奇吗？大家可别小瞧了这看似简单的幅角原理，它里面蕴含的智慧可多着呢！就像一个宝藏，等着你去挖掘。
咱再深入想想，这生活中不也到处都是类似幅角原理的智慧吗？有时候一个小小的方法，就能解决大问题。
就好像一把钥匙开一把锁，找对了方法，什么难题都能轻松搞定。
总之啊，幅角原理例题讲解真的很重要，很有趣，也很实用。
大家可得好好学，好好用，让它成为我们解决问题的得力助手。
相信我，一旦你掌握了它，你就会发现数学的世界更加精彩啦！。
幅角原理闭合曲线外零极点
幅角原理是复分析中的一个重要原理，它主要用于研究闭合曲线（如解析曲线）与原点之间的关系。
幅角原理指出，闭合曲线外的零极点分布与曲线内部的角度分布密切相关。
首先，我们来了解一下零极点。
在复平面上，零点是指函数值为零的点，而极点是指函数值为无穷大的点。
对于一个解析函数，其在复平面上的零点和极点分别表示为：
Z = {z | f(z) = 0}
P = {z | f(z) → ∞ as z → z'}
其中，f(z)为解析函数，z为复数，z'为z的共轭复数。
幅角原理表明，闭合曲线外的零极点与曲线内部的角度分布具有以下关系：
1. 零点：闭合曲线外的零点分布在单位圆上的角度与曲线内部零点的角度相等。
即，对于曲线上的任意一点θ，其对应的单位圆上的零点为e^(jθ)。
2. 极点：闭合曲线外的极点分布在单位圆上的角度与曲线内部极点的角度相等。
即，对于曲线上的任意一点θ，其对应的单位圆上的极点为e^(j(π - θ))。
幅角原理的应用广泛，例如在复分析、信号处理、图像处理等领域。
通过研究闭合曲线外的零极点分布，我们可以更好地理解曲线内部的结构和性质，为实际问题的求解提供理论依据。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（一）授课思路（三）讲解要点及各部分具体内容：
一幅角原理
1.亚纯函数
定义1设 在区域内除了有极点外处处解析，则称为亚纯函数
例如，有理函数，
全纯函数可看作亚纯函数的特例。
引理1，设 在环线 上解析且不为零，在 内部亚纯，则 在 内部只有有限个零点与极点。
引理2.设a为f的n级零点，则 必是 的一级极点，且
授课题目
§3幅角原理及其应用
授课类型
理论课
首次授课时间
2009年12月10日
学时
2
教学目标
掌握复变函数积分的概念,积分存在的条件及积分计算法和性质.
重点与难点
重点：复变函数积分存在的条件及其计算法和性质.
难点：复变函数计算法和性质.
教学手段与方法
黑板
讲授
教学过程：（包括授课思路、过程设计、讲解要点及各部分具体内容、时间分配等）
（2.）令 ，则
所以 = = =
推论：若 在 内部解析，则
注:辐角原理中的条件2）可减弱为： 连续到 上，且 在 上
例8：设 ： 试验试辐角原理
解： 满足辐角原理条件。又
3.儒歇定理
定理6.2设 为围线， 与 满足：1）它们在 内解析，且连续到 ，
2）在 上 ，则
证明：由已知条件， 与 都在 内部解析，且连续到
2） 在 上解析，且不取零，则
.
（其中 与 分别表示 在 内部零点个数与极点个数几级算几个）
证明：（1）由已知条件知， 在内至多只能有有限个零点与有限个极点，设 为 在 内部不同的零点，其级分别为 ， 为 在 内部不同的极点，其级分别为 ，由引理知， 在 上解析。在 内部除了一级极点， 与 处均解析.由留数定理，得
2）设b是f的m级极点，则b必是 的一级极点，且 .
证：由所设，1）在 的某个领域内，有 .其中 在 的领域内解析，且 .
即 ,由 在 点解析便知： 是 的一级极点，且 .
2)由所设在 的某去心领域内，有 ,其中 在 的某去心领域内解析，且 ,于是 .
由于 在 点解析,故 为 的一级极点，且
定理6.1设 为围线， 满足1） 在 内除可能极点外解析;
6.证明方程 的所有根都在圆环 内。
教学后记
在 上， ，
要证明 即可
但
故只要证明
记 ，它把 变为 平面上曲线
但 故 不会绕平面原点 .
从而
例9：求 在内根个数
解：设 ，则它们在 内解析连续到 ： ，在 上，
由儒歇定理，
例10：判断 在 有几个根
解：设=a0zn+a1zn-1+…+an=0(a0≠0）
在虚轴上没有零点， ， 为虚轴上从 指向 的路径，
证明它的全部零点在左半平面Rez<0内
3.设 内解析，且 ，证明 在 内必有不动点。
4.证明： 在右半平面恰好有一个根。
5n次方程(p(z)=)a0zn+a1zn-1+…+an=0(a0≠0）
在复数域内有且仅有n个根（几重根就算几个根
首先证明存在R>0，方程在圆|z|<R内恰有n个根
其次证明，对z0 |z0|=R0≥R，均有|p(z0)|>0
一幅角原理
1.亚纯函数
定义1设 在区域内除了有极点外处处解析，则称为亚纯函数
例如，有理函数，
全纯函数可看作亚纯函数的特例。
引理1，设 在环线 上解析且不为零，在 内部亚纯，则 在 内部只有有限个零点与极点。
引理2.设a为f的n级零点，则 必是 的一级极点，且
授课题目
§3幅角原理及其应用
授课类型
理论课
首次授课时间
2009年12月10日
学时
2
教学目标
掌握复变函数积分的概念,积分存在的条件及积分计算法和性质.
重点与难点
重点：复变函数积分存在的条件及其计算法和性质.
难点：复变函数计算法和性质.
教学手段与方法
黑板
讲授
教学过程：（包括授课思路、过程设计、讲解要点及各部分具体内容、时间分配等）
（2.）令 ，则
所以 = = =
推论：若 在 内部解析，则
注:辐角原理中的条件2）可减弱为： 连续到 上，且 在 上
例8：设 ： 试验试辐角原理
解： 满足辐角原理条件。又
3.儒歇定理
定理6.2设 为围线， 与 满足：1）它们在 内解析，且连续到 ，
2）在 上 ，则
证明：由已知条件， 与 都在 内部解析，且连续到
2） 在 上解析，且不取零，则
.
（其中 与 分别表示 在 内部零点个数与极点个数几级算几个）
证明：（1）由已知条件知， 在内至多只能有有限个零点与有限个极点，设 为 在 内部不同的零点，其级分别为 ， 为 在 内部不同的极点，其级分别为 ，由引理知， 在 上解析。在 内部除了一级极点， 与 处均解析.由留数定理，得
2）设b是f的m级极点，则b必是 的一级极点，且 .
证：由所设，1）在 的某个领域内，有 .其中 在 的领域内解析，且 .
即 ,由 在 点解析便知： 是 的一级极点，且 .
2)由所设在 的某去心领域内，有 ,其中 在 的某去心领域内解析，且 ,于是 .
由于 在 点解析,故 为 的一级极点，且
定理6.1设 为围线， 满足1） 在 内除可能极点外解析;
6.证明方程 的所有根都在圆环 内。
教学后记
在 上， ，
要证明 即可
但
故只要证明
记 ，它把 变为 平面上曲线
但 故 不会绕平面原点 .
从而
例9：求 在内根个数
解：设 ，则它们在 内解析连续到 ： ，在 上，
由儒歇定理，
例10：判断 在 有几个根
解：设=a0zn+a1zn-1+…+an=0(a0≠0）
在虚轴上没有零点， ， 为虚轴上从 指向 的路径，
证明它的全部零点在左半平面Rez<0内
3.设 内解析，且 ，证明 在 内必有不动点。
4.证明： 在右半平面恰好有一个根。
5n次方程(p(z)=)a0zn+a1zn-1+…+an=0(a0≠0）
在复数域内有且仅有n个根（几重根就算几个根
首先证明存在R>0，方程在圆|z|<R内恰有n个根
其次证明，对z0 |z0|=R0≥R，均有|p(z0)|>0