钻井布局问题的搜索算法
- 格式:pdf
- 大小:233.28 KB
- 文档页数:6

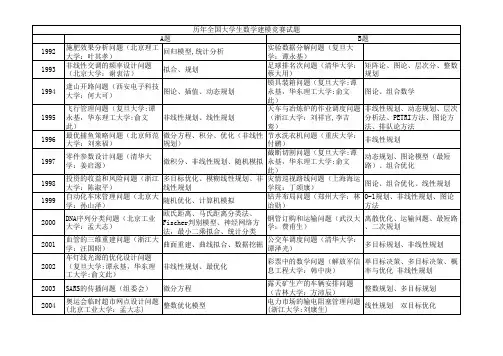
历届数学建模题目浏览:1992--20091992年 (A) 施肥效果分析问题(北京理工大学:叶其孝)(B) 实验数据分解问题(华东理工大学:俞文此; 复旦大学:谭永基)1993年 (A) 非线性交调的频率设计问题(北京大学:谢衷洁)(B) 足球排名次问题(清华大学:蔡大用)1994年 (A) 逢山开路问题(西安电子科技大学:何大可)(B) 锁具装箱问题(复旦大学:谭永基,华东理工大学:俞文此)1995年 (A) 飞行管理问题(复旦大学:谭永基,华东理工大学:俞文此)(B) 天车与冶炼炉的作业调度问题(浙江大学:刘祥官,李吉鸾)1996年 (A) 最优捕鱼策略问题(北京师范大学:刘来福)(B) 节水洗衣机问题(重庆大学:付鹂)1997年 (A) 零件参数设计问题(清华大学:姜启源)(B) 截断切割问题(复旦大学:谭永基,华东理工大学:俞文此)1998年 (A) 投资的收益和风险问题(浙江大学:陈淑平)(B) 灾情巡视路线问题(上海海运学院:丁颂康)1999年 (A) 自动化车床管理问题(北京大学:孙山泽)(B) 钻井布局问题(郑州大学:林诒勋)1999年(C) 煤矸石堆积问题(太原理工大学:贾晓峰)(D) 钻井布局问题(郑州大学:林诒勋)2000年 (A) DNA序列分类问题(北京工业大学:孟大志)(B) 钢管订购和运输问题(武汉大学:费甫生)(C) 飞越北极问题(复旦大学:谭永基)(D) 空洞探测问题(东北电力学院:关信)2001年 (A) 血管的三维重建问题(浙江大学:汪国昭)(B) 公交车调度问题(清华大学:谭泽光)(C) 基金使用计划问题(东南大学:陈恩水)(D) 公交车调度问题(清华大学:谭泽光)2002年 (A) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此)(B) 彩票中的数学问题(解放军信息工程大学:韩中庚)(C) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此)(D) 赛程安排问题(清华大学:姜启源)2003年 (A) SARS的传播问题(组委会)(B) 露天矿生产的车辆安排问题(吉林大学:方沛辰)(C) SARS的传播问题(组委会)(D) 抢渡长江问题(华中农业大学:殷建肃)2004年 (A) 奥运会临时超市网点设计问题(北京工业大学:孟大志)(B) 电力市场的输电阻塞管理问题(浙江大学:刘康生)(C) 酒后开车问题(清华大学:姜启源)(D) 招聘公务员问题(解放军信息工程大学:韩中庚)2005年 (A) 长江水质的评价和预测问题(解放军信息工程大学:韩中庚)(B) DVD在线租赁问题(清华大学:谢金星等)(C) 雨量预报方法的评价问题(复旦大学:谭永基)(D) DVD在线租赁问题(清华大学:谢金星等)2006年 (A) 出版社的资源配置问题(北京工业大学:孟大志)(B) 艾滋病疗法的评价及疗效的预测问题(天津大学:边馥萍)(C) 易拉罐的优化设计问题(北京理工大学:叶其孝)(D) 煤矿瓦斯和煤尘的监测与控制问题(解放军信息工程大学:韩中庚)2007年 (A) 中国人口增长预测(B) 乘公交,看奥运(C) 手机“套餐”优惠几何(D) 体能测试时间安排2008年(A)数码相机定位,(B)高等教育学费标准探讨,(C)地面搜索,(D)NBA赛程的分析与评价2009年(A)制动器试验台的控制方法分析(B)眼科病床的合理安排(C)卫星和飞船的跟踪测控(D)会议筹备历年全国数学建模试题及解法归纳赛题解法93A非线性交调的频率设计拟合、规划93B足球队排名图论、层次分析、整数规划94A逢山开路图论、插值、动态规划94B锁具装箱问题图论、组合数学95A飞行管理问题非线性规划、线性规划95B天车与冶炼炉的作业调度动态规划、排队论、图论96A最优捕鱼策略微分方程、优化96B节水洗衣机非线性规划97A零件的参数设计非线性规划97B截断切割的最优排列随机模拟、图论98A一类投资组合问题多目标优化、非线性规划98B灾情巡视的最佳路线图论、组合优化99A自动化车床管理随机优化、计算机模拟99B钻井布局 0-1规划、图论00A DNA序列分类模式识别、Fisher判别、人工神经网络00B钢管订购和运输组合优化、运输问题01A血管三维重建曲线拟合、曲面重建赛题解法01B 公交车调度问题多目标规划02A车灯线光源的优化非线性规划02B彩票问题单目标决策03A SARS的传播微分方程、差分方程03B 露天矿生产的车辆安排整数规划、运输问题04A奥运会临时超市网点设计统计分析、数据处理、优化04B电力市场的输电阻塞管理数据拟合、优化05A长江水质的评价和预测预测评价、数据处理05B DVD在线租赁随机规划、整数规划06A出版社书号问题整数规划、数据处理、优化06B Hiv病毒问题线性规划、回归分析07A 人口问题微分方程、数据处理、优化07B 公交车问题多目标规划、动态规划、图论、0-1规划08A 照相机问题非线性方程组、优化08B 大学学费问题数据收集和处理、统计分析、回归分析赛题发展的特点:1. 对选手的计算机能力提出了更高的要求:赛题的解决依赖计算机,题目的数据较多,手工计算不能完成,如03B,某些问题需要使用计算机软件,01A。

1.问题描述
某石油公司计划建造一条由东向西的输油管道,该管道要穿过一个有n口油井的油田。
从每口油井都要有一条输油管道沿最短路径(南北方向)与主管道相连。
如果给定n口油井的位置,即它们的x坐标和y坐标。
设计一个算法来确定主管道的位置,使得每口油井到主管道之间的输油管道长度之和达到最小。
2.实验任务
给定n个x,y坐标,找出一条线使得n个点到线的距离之和最短
3.解题思路
将n个坐标进行排序,n个坐标中中间的那个点就是所找线的位置所在,所以用快排对坐标进行排序算法实
4.算法分析
5.代码实现。

建模十大经典算法1、蒙特卡罗算法。
该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时通过模拟可以来检验自己模型的正确性。
2、数据拟合、参数估计、插值等数据处理算法。
比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具。
3、线性规划、整数规划、多元规划、二次规划等规划类问题。
建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo、MATLAB软件实现。
4、图论算法。
这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备。
5、动态规划、回溯搜索、分治算法、分支定界等计算机算法。
这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中。
6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法。
这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用。
7、网格算法和穷举法。
网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具。
8、一些连续离散化方法。
很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9、数值分析算法。
如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10、图象处理算法。
赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理。
历年全国数学建模试题及解法赛题解法93A非线性交调的频率设计拟合、规划93B足球队排名图论、层次分析、整数规划94A逢山开路图论、插值、动态规划94B锁具装箱问题图论、组合数学95A飞行管理问题非线性规划、线性规划95B天车与冶炼炉的作业调度动态规划、排队论、图论96A最优捕鱼策略微分方程、优化96B节水洗衣机非线性规划97A零件的参数设计非线性规划97B截断切割的最优排列随机模拟、图论98A一类投资组合问题多目标优化、非线性规划98B灾情巡视的最佳路线图论、组合优化99A自动化车床管理随机优化、计算机模拟99B钻井布局0-1规划、图论00A DNA序列分类模式识别、Fisher判别、人工神经网络00B钢管订购和运输组合优化、运输问题01A血管三维重建曲线拟合、曲面重建01B 公交车调度问题多目标规划02A车灯线光源的优化非线性规划02B彩票问题单目标决策03A SARS的传播微分方程、差分方程03B 露天矿生产的车辆安排整数规划、运输问题04A奥运会临时超市网点设计统计分析、数据处理、优化04B电力市场的输电阻塞管理数据拟合、优化05A长江水质的评价和预测预测评价、数据处理05B DVD在线租赁随机规划、整数规划06A 出版资源配置06B 艾滋病疗法的评价及疗效的预测 07A 中国人口增长预测 07B 乘公交,看奥运 多目标规划 数据处理 图论 08A 数码相机定位 08B 高等教育学费标准探讨09A 制动器试验台的控制方法分析 09B 眼科病床的合理安排 动态规划 10A 10B赛题发展的特点:1.对选手的计算机能力提出了更高的要求:赛题的解决依赖计算机,题目的数据较多,手工计算不能完成,如03B ,某些问题需要使用计算机软件,01A 。

钻井布局方案最优化方法钻井是一项复杂的地质工程,需要考虑许多因素,比如地质条件、钻探设备、工人技能、工期成本等等。
为了提高钻井效率和质量,需要利用先进的优化方法,来选择最优的钻井布局方案。
钻井布局方案优化的局限性钻井布局方案优化是一项多因素决策问题,不同的权衡和限制因素会影响到钻井方案的选择和设计。
因此,优化目标和优化方法一定要考虑到以下几个因素:•地质条件:包括地形、地质构造、地层状况、地下水位等因素;•钻探设备:包括钻机类型、钻头规格、钻杆长度等工具设备因素;•工人技能:包括工人的技能水平、工作经验、技术素质等个人因素;•工期成本:包括项目周期、人工费用、材料费用、能源费用等项目成本。
钻井布局方案的优化目标往往是复合型的,不同的优化组合和方案可能会导致不同的优化结果和效果。
因此,钻井布局方案的优化方法必须考虑到这些因素的限制和局限性。
钻井布局方案优化的方法与原理在钻井布局方案的优化中,常见的优化方法有两种,一种是基于规则的优化方法,另一种是基于模型的优化方法。
基于规则的优化方法基于规则的优化方法是一种常见的方法,它借助手工创造的规则和经验来处理钻井布局方案的优化问题。
这种方法往往需要依赖于专家和经验和规则,因此会受制于规则显示缺陷、专家经验不足、数据资料不全等因素。
基于模型的优化方法基于模型的优化方法是一种常见的优化技术,它通常利用计算机化模型来对钻井布局方案进行数据分析和计算处理。
在这种方法中,模型会结合不同的优化算法和策略,对多种指标进行分析,以确定最优的钻井布局方案。
这种方法的优点在于可更新、可测量、可重复复现等多重优势。
基于模型的优化方法中,常见的优化算法包括:遗传算法、模拟退火算法、蚁群算法、粒子群算法等。
这些算法均具有进化和搜索的特点,适合处理多因素决策问题下的优化方案。
钻井布局方案优化的案例下面以某工程集团某钻探项目为例,介绍如何利用上述方法对钻井布局方案进行优化。
该工程集团的钻井项目地理位置特殊,周边地质条件复杂,需要考虑到地形起伏、地下水位、气候和环境影响等因素。

建模更是一种精神】数学建模全国大赛历年题目分析以及参赛成功方法数学建模竞赛的赛题分析1. CUMCM历年赛题简析2. “彩票中的数学”问题3. 长江水质的评估、预测与控制问题4. 煤矿瓦斯和煤尘的监测与控制问题5. 其他几个数学建模的问题数学建模竞赛的规模越来越大,水平越来越高;竞赛的水平主要体现在赛题水平;赛题的水平主要体现:(1)综合性、实用性、创新性、即时性等;(2)多种解题方法的创造性、灵活性、开放性等;(3)海量数据的复杂性、数学模型的多样性、求解结果的不唯一性等。
纵览16年的本科组32个题目(专科组13个),从问题的实际意义、解决问题的方法和题型三个方面作一些简单的分析。
一、CUMCM历年赛题的简析1. CUMCM 的历年赛题浏览:1992年:(A)作物生长的施肥效果问题(北理工:叶其孝)(B)化学试验室的实验数据分解问题(复旦:谭永基)1993年:(A)通讯中非线性交调的频率设计问题(北大:谢衷洁)(B)足球甲级联赛排名问题(清华:蔡大用)1994年:(A)山区修建公路的设计造价问题(西电大:何大可)(B)锁具的制造、销售和装箱问题(复旦:谭永基等)1995年:(A)飞机的安全飞行管理调度问题(复旦:谭永基等)(B)天车与冶炼炉的作业调度问题(浙大:刘祥官等)一、CUMCM历年赛题的简析1. CUMCM 的历年赛题浏览:1996年:(A)最优捕鱼策略问题(北师大:刘来福)(B)节水洗衣机的程序设计问题(重大:付鹂)1997年:(A)零件参数优化设计问题(清华:姜启源)(B)金刚石截断切割问题(复旦:谭永基等)1998年:(A)投资的收益和风险问题(浙大:陈淑平)(B)灾情的巡视路线问题(上海海运学院:丁颂康)1999年:(A)自动化机床控制管理问题(北大:孙山泽)(B)地质堪探钻井布局问题(郑州大学:林诒勋)(C)煤矸石堆积问题(太原理工大学:贾晓峰)一、CUMCM历年赛题的简析1. CUMCM 的历年赛题浏览:2000年:(A)DNA序列的分类问题(北工大:孟大志)(B)钢管的订购和运输问题(武大:费甫生)(C)飞越北极问题(复旦:谭永基)(D)空洞探测问题(东北电力学院:关信)2001年:(A)三维血管的重建问题(浙大:汪国昭)(B)公交车的优化调度问题(清华:谭泽光)(C)基金使用计划问题(东南大学:陈恩水)2002年:(A)汽车车灯的优化设计问题(复旦:谭永基等)(B)彩票中的数学问题(信息工程大学:韩中庚)(D) 球队的赛程安排问题(清华大学:姜启源)一、CUMCM历年赛题的简析1. CUMCM 的历年赛题浏览2003年:(A)SARS的传播问题(集体)(B)露天矿生产的车辆安排问题(吉林大:方沛辰)(D)抢渡长江问题(华中农大:殷建肃)2004年:(A)奥运会临时超市网点设计问题(北工大:孟大志)(B)电力市场的输电阻塞管理问题(浙大:刘康生)(C)酒后开车问题(清华大学:姜启源)(D)公务员的招聘问题(信息工程大学:韩中庚)2005年:(A)长江水质的评价与预测问题(信息工大:韩中庚)(B)DVD在线租赁问题(清华大学:谢金星等)(C) 雨量预报方法的评价问题(复旦:谭永基)一、CUMCM历年赛题的简析1. CUMCM 的历年赛题浏览2006年:(A)出版社的资源管理问题(北工大:孟大志)(B)艾滋病疗法的评价及预测问题(天大:边馥萍)(C)易拉罐形状和尺寸的设计问题(北理工:叶其孝)(D)煤矿瓦斯和煤尘的监测与控制问题(信息工程大学:韩中庚)2007年:(A)中国人口增长预测问题(清华大学:唐云)(B)“乘公交,看奥运”问题(吉大:方沛辰,国防科大:吴孟达)(C)“手机套餐”优惠几何问题(信息工程大学:韩中庚)(D)体能测试时间的安排问题(首都师大:刘雨林)一、CUMCM历年赛题的简析一、CUMCM历年赛题的简析1. CUMCM 的历年赛题浏览2001年夏令营三个题:(A)三峡工程高坡开挖优化设计(三峡大学:李建林等)(B)城市交通拥阻的分析与治理(北京理工大学:叶其孝)(C)乳房癌的诊断问题(复旦大学:谭永基)2006年夏令营三个题:(A)教材出版业的市场调查、评估和预测方法问题(北工大:孟大志)(B)铁路大提速下的京沪线列车调度问题(信息工程大学:韩中庚)(C)旅游需求的预测预报问题(北京理工:叶其孝)2、从问题的实际意义分析32个问题从实际意义分析大体上可分为:工业、农业、工程设计、交通运输、经济管理、生物医学和社会事业等七个大类。

矿井布局问题的数学模型摘要勘探部门在某地区找矿时,首先进行初步勘探,取几个位置钻井,取得地质资料;然后进行系统勘探,进行纵横等距的撒网式钻井。
显然如果能尽可能多的在系统勘探时利用初步勘探的钻井资料,就能有效的节约费用。
在不考虑网格方向的情况下,本文首先给出了两个定理,即网格的位置由节点唯一确定与原始点与单位方格内的映射点有相同的性质。
这样就将问题等效为在单位方格内确定网格的一个节点。
要解决这个问题,首先我们提出运用一般的搜索法对网格节点在单位方格内进行搜索(模型一)。
通过对搜索法进行有效的优化,大量减少了搜索的次数,进而计算得到了原井位最多有4个可被利用,并给出了方格节点的坐标为:Z ∈++n m n m , )50.0,40.0(考虑到搜索法的复杂度,我们给出了模型二,即在单位方格内通过确定每个映射点被利用时节点的区域,来找出方格内被这些区域覆盖次数最高的部分,显然如果将节点放在这部分内,将会有最多的点被利用,从而也就确定了节点的位置范围。
运用MATLAB 进行计算与判别,得到最多有4个可被利用,并求出了网格节点坐标的范围:Z ∈∈∈++n m y x n y m x , )55.0,46.0(),42.0,36.0( ),(其中当网格方向可以改变时,我们建立了模型三。
考虑如果对角度进行遍历搜索,再用模型二进行判断,那么就能相应的找到最优角度。
模型三首先进行了误差分析,确定了角度搜索的合适步长;然后,为了减小搜索范围,我们证明了在区间[0,90)与区间[0,360)上搜索是等价的,都可以找到最优解;最后通过计算,我们得到当网格顺时针旋转 45,并将一个节点定位在)75.0,93.0(时,最多有6个矿井可被利用。
考虑到暴力搜索的复杂性,我们希望改进搜索方法,这样,作为模型三的优化,我们应用了遗传算法。
遗传算法通过模拟生物进化,在搜索时有一定的选择性,能够较快的得到最优解。
我们通过对角度的二进制编码进行复制,交换与突变,在计算了60代后,得到了最多利用点的个数也为6。

钻井计算公式〔精典〕1.卡点深度:L=eEF/105P=K×e/P式中:L-----卡点深度米e------钻杆连续提升时平均伸长厘米E------钢材弹性系数=2.1×106公斤/厘米2F------管体截面积。
厘米2P------钻杆连续提升时平均拉力吨K------计算系数K=EF/105=21F钻具被卡长度l:l=H-L式中H-----转盘面以下的钻具总长米注:K值系数5"=715〔9.19〕例:*井在井深2000米时发生卡钻,井内使用钻具为壁厚11毫米的59/16"钻杆,上提平均拉力16吨,钻柱平均伸长32厘米,求卡点深度和被卡钻具长度。
解:L=Ke/P由表查出壁厚11毫米的59/16"钻杆的K=957则:L=957×32/16=1914米钻具被卡长度:L=H-L=2000-1914=86米2、井内泥浆量的计算V=D2H/2或V=0.785D2H3、总泥浆量计算Q=q井+q管+q池+q备4、加重剂用量计算:W加=r加V原(r重-r原)/r加-r重式中:W加----所需加重剂的重量,吨r原----加重前的泥浆比重,r重----加重后的泥浆比重r加---加重料的比重V原---加重前的泥浆体积米3例:欲将比重为1.25的泥浆200米3,用比重为4.0的重晶石粉加重至1.40,需重晶石假设干?解:根据公式将数据代入:4×200〔〕/4.0-1.40=46吨5.降低泥浆比重时加水量的计算q=V原(r原-r稀)/r稀-r水式中:q----所需水量米3V原---原泥浆体积米3r稀---稀释后泥浆比重r水----水的比重〔淡水为1〕r原---原泥浆比重例:欲将比重1.30的泥浆150米3降至比重为1.17,需加淡水假设干?解:根据公式代入数据:150〔〕×1/1.17-1=115米36、泥浆循环一周所需时间计算T=V井-V柱/60Q泵式中:T---泥浆循环一周的时间,分V井---井眼容积,升V柱---钻柱体积升Q泵---泥浆泵排量升/秒备注:V井=0.785D井2V柱=0.785〔D外2-d内2〕例题:井径81/2",使用壁厚为10毫米的41/2"钻至1000米,泵的排量为21.4升/秒,问泥浆循环一周需时假设干?解: V井=0.785×〔215.9〕2=36591升V柱=0.785〔114.32-94.32〕=3275升T= V井-V柱/60Q泵=36591-3275/60×21.4=33316/1284=25.95分7、泥浆上返速度计算V返=12.7Q泵/D井2-d柱2式中:V返—泥浆上返速度米/秒Q泵---泥浆泵排量升/秒D井---井径厘米d柱---钻柱外径厘米例题:*井井径为22厘米,钻具外径为11.4厘米,泥浆泵排量为25升/秒,问泥浆上返速度是多少?解:V返=12.7Q泵/D井2-d柱2=12.7×25/222-11.42=0.90米/秒8、漏失速度计算公式:V漏=Q漏/t时式中:V漏—漏失速度米3/小时Q漏---在*段时间内的漏失量米3t时----漏失时间小时例题:*井在30分钟内共漏泥浆15.6米3问该井在这段时间内的漏失速度是多少?解:V漏=Q漏/t时=15.6/0.5=31.2米3/小时9、泵压计算公式:P=0.081ρQ2/0.96D4式中:P---泵压 MPaρ---使用密度 g/cm3Q----泥浆泵排量 l/sD---钻头水眼毫米D=√d12+d22+d32+…..10.常用套管数据表11.接头扣型尺寸:〔1:内平 2:贯眼 3:正规〕12.常用单位换算表长度:1英寸(in)=25.4毫米(mm)=2.54厘米(cm)=0.0254米(m)1英尺(ft)=12英寸(in)=304.8毫米(mm)=30.48厘米(cm)=0.3048米(m) 1码(yd)=3英尺(ft)=914.4毫米(mm)=91.44厘米(cm)=0.9144米(m)1里=150丈=500米1丈=3.33米1尺=0.33米1寸=0.033米面积:1亩=666.6m²13.常规井身构造有效井眼直径 =〔钻头直径 +钻铤直径〕÷20在大于215.9mm(81/2in)的井眼中,应采用塔式钻铤组合,钻铤柱中最下一段钻铤(一般应不少于1立柱)的外径应不小于这一允许最小外径,才能保证套管的顺利下入。

第30卷第1期2000年1月数学的实践与认识M A TH EM A T I CS I N PRA CT I CE AND TH EO R YV o l130 N o11 Jan.2000 p rob lem,the ob jective functi om is bu ilt.W e p resen t the m app ing p rinci p le,to m ap the locati on s of the o riginalw ells in to a un ique un it b lock of the m esh,so as to si m p lify the so lu ti on of the model.U sing the m app ing algo rithm and the ergodic algo rithm,w e so lve the p rob lem under the directi on con strain t.T hen w e generalize the algo rithm s to the so lu ti on w ithou t the directi on con strain t.W e studied the sufficien t conditi on s and give som e criteria of the availab ility on th ree particu lar condi2 ti on s.T he m ethod of b isecti on on perpendicu lar at m idpo in t is p resen ted.钻井布局的数学模型胡海洋, 陈 建, 陆 鑫指导教师: 陈 晖, 姚天行(南京大学,南京 210093)摘要: 本文对钻井布局问题的研究,是从全局搜索入手,逐步深入讨论了各种算法的有效性、适用性和复杂性,得到不同条件下求最多可利用旧井数的较好算法.对问题1,我们给出了全局搜索模型、局部精化模型与图论模型,讨论了各种算法的可行性和复杂度.得到的答案为:最多可使用4口旧井,井号为2,4,5,10.对问题2,我们给出了全局搜索、局部精化和旋转矢量等模型,并对局部精化模型给出了理论证明,答案为:最多可使用6口旧井,井号为1,6,7,8,9,11,此时的网格逆时针旋转44.37度,网格原点坐标为(0.47,0.62).对问题3,给出判断n口井是否均可利用的几个充分条件、必要条件和充要条件及其有效算法.1 模型假设及符号说明(略)2 问题分析与模型准备如果一个已知点P i与某个网络结点X j距离不超过给定误差Ε(0105)单位,则认为P i 处的旧井资料可以利用.因此,在棋盘(欧氏)距离定义下,可以以P i为中心,2Ε单位为边长作一个正方形(半径为Ε的圆).若网络在平移过程中,网络中的某个结点X j落在以P i为中心的正方形(圆)内或边上,可认为X j可利用旧井P i的相应资料.同样可以以X j为中心,2Ε单位为边长作一个正方形(圆).若网络在平移过程中,P i落在以X j为中心的正方形(圆)内或边上,可认为X j可利用旧井P i的相应资料.这两种方法分别对应于网格移动和坐标平移,显然它们是等价的.以下的讨论将不明显区别这两种方法.为了简化讨论,引入以下法则.映射法则:将点i映射至以(a,b),(a+1,b+1)为对角顶点的正方形内的点i′,i′x=i x-[i x]+a; i′y=i y-[i y]+b,其中[x]为x的整数部分.覆盖法则:将所有旧井映射至(-1,-1),(0,0);(-1,0),(0,1);(0,-1),(1,0);(0,0),(1,1)为对角顶点的四个正方形上.以2Ε为边长作小正方形,该正方形形心在以(-015,-015),(015,015)为对角顶点的正方形内移动,则可被正方形所覆盖的映射点为可同时利用的点.这样的正方形称为判决正方形或判决方块.相应的,在第二问中采用一个半径为Ε的圆移动来覆盖映射点,称为判决圆.映射法则和覆盖法则是易于理解也是易于证明的.下面我们讨论时都应用了映射法则和覆盖法则,将点映射后在映射区间内判断旧井是否可利用.3 模型的建立311 对问题一的讨论11目标函数的给出设网络的起点为(a ,b ),地域中某旧井P i 坐标为(P ix ,P iy ),则该旧井可利用的条件是:a +N i -Ε≤P ix ≤a +N i +Ε 且b +N j -Ε≤P iy ≤b +N j +Ε,其中N i 和N j 为非负整数.令函数M (X i ,Y i )=1,a +N i -Ε≤X i ≤a +N i +Ε,b +N j -Ε≤Y i ≤b +N i +Ε0,其它由于问题要求寻找尽量多的可利用旧井点,因此,建立目标函数如下:F (a ,b )=m ax ∑ni =1M(X i ,Y i ).根据以上的分析,可以建立以下模型.21模型一:枚举法在本题中,由于精度的要求为0101,且网格可上下、左右平行移动.因此可按纵、横坐标方向分别平移100次(即1个单位长),用覆盖法对区域中的所有12个旧井点搜索,如覆盖旧井点,则记录覆盖数.最后比较在这100×100次平移中,哪一次覆盖数最大,则该网格位置为最优.该算法的复杂度为O n Θ2,n 为旧井数,Θ为数值的要求精度,在本题中为0101.计算结果如下:网格节点为(0136,0146),最多可利用旧井数为4,分别是2,4,5,10号井.枚举法对精度要求不高时,颇为有用,但当精度要求很高时,往往较为复杂.在模型一的基础上,我们进行了部分改进,提出模型二及其算法.31模型二:部分穷举法显然对12个旧井点中的任一个井点都存在一个网格,使得该井点可被该网格所用.因此可以在P i 已被该网格利用的情况下,再去检查其它旧井点能否被该网格所利用.因此,可将网格中一个结点放在以该点为中心,2Ε为边长的一个正方形区域中,再去测试其它旧井点是否满足条件.对于一个而言,网格某个结点,在以该点为中心,2Ε为边长的正方形区域中有(2Ε Θ)2种放置法.这样即得部分穷举法的复杂度为O (n 2(Ε Θ)2).部分穷举法抓住一个旧井点后考察其它旧井点的情况.因此,它比全部穷举法优点在于:避免了对所有旧井点均不可利用的情形的搜索.但该算法的缺点在于n 不能太大,否则可能得不偿失,使计算量度大为增加.计算结果与模型一相同.161期胡海洋等:钻井布局的数学模型41模型三:部分穷举法在模型二中我们根据至少利用一个点的原则移动判决方块.在本模型中我们在至少有两口井可用情况下,由两口井确定一个判决方块,进而进一步缩减计算量.定理1.3.1 在覆盖点数最多的判决方块中必有一个方块A满足下述两条之一:(1)有两点P i与P j分别在A的左边框和下边框上;(2)有一点P i在A的左下顶点处.该定理的证明从直观上看是显然的,若某判决方块A′覆盖的点数最多,将A′连续向右和向上移动,直至若继续移动将会有点跑出为止,此时A′的位置记为A,则A必适合定理中两条件之一,且A中点数也是最多的.由此定理,我们只需在所有以两点确定左边框和下边框的判决方块和以一点为左下顶点确定的判决方块的覆盖数之间进行比较,最大者即为最多可利用旧井数.该方法对于n个井点,需计算约(C2n+n)n,复杂度为O(n3),是与精度无关的算法.计算结果同上.51模型四:涂层法由映射法则,P i,P j的映射点在正方形[(-Ε,-Ε);(1+Ε,1+Ε)]内为P′i,P′j,则P i,P j 可用的充要条件是d(P′i,P′j)≤2Ε,即分别以P′i,P′j为心,边长2Ε的两个正方形相交.对于n 个点,则这n个点都可用的充要条件是以这n个点为中心的正方形都相叠.以相叠部分为网格点,总可以利用这n个点.本模型即用这样的思路,计算最多有多少正方形相叠,并以相叠部分中的一点以网格结点作网格.算法思想:用矩阵A表示[(-Ε,-Ε);(1+Ε,1+Ε)],将点离散化,以精度Θ取样.则A表示为1+2ΕΘ阶零矩阵.用全1矩阵a表示以映射点P′j为中心,2Ε为边长的小方形.则将这些小矩阵加到大矩阵的相应位置上去,即相当于把小正方形“涂”到大框里.则A中某点上数字之和即表示该点被多少正方形覆盖,也即以该点为起点的网格可利用多少旧井.找出A 中数字最大者,即为最大利用旧井数,该点为最优网格的起始点.该算法复杂度为O n(Ε Θ)2.在精度不太高时计算是迅速的.精度高时,对内存和速度都有较高要求.计算结果同上.61模型五:图论模型.定理1.5.1 作一无向图G[V,E],V为旧井点的集合.若第i与第j号井可同时利用,则在i,j之间加一条边.则可同时利用的井点组成一个完全子图,即团.在棋盘距离下最多可利用旧井数等于最大团的阶数.证明 (略).此定理对欧氏距离不适用.由此定理可得到下述推论.推论 在棋盘距离下,若某些旧井两两可同时利用,则这些旧井可被同时利用.由此提出图论模型如下:按定理11511构造图G,找最大完全子图.首先,找出可同时利用的旧井对.可利用下述定理求得.定理1.5.2 P i,P j均可以在某网络中被利用的充要条件是存在非负整数N1,N2,使得:26数 学 的 实 践 与 认 识30卷d x (P i ,P j )∈[N1-2Ε,N 1+2Ε],d y (P i ,P j )∈[N 2-2Ε,N 2+2Ε],其中d x 与d y 分别表示x 方向与y 方向距离.证明 (略)1下述定理是图论中熟知的定理.定理11513 设G 是n 阶无向图,V 3为G 中极大(最大)团当且仅当V 3为G 的中的极大(最大)独立集,其中G 是G 的补图.因此,问题归结为寻找G 中的最大独立集.但寻找最大独立集为N P 问题,目前尚无好的方法.图论模型优点在于:它在理论上是完备与精确的,不受数值精度与Ε的影响.71五个模型的比较对于五个模型的比较,我们认为模型三、四、五是较优的.模型三与精度无关,复杂度为O n 3.对于大多数情况都是适用的.模型四与精度有关.复杂度为O n ,Ε Θ2,在本题中Ε Θ=5.在精度要求不太高,且点数较多时,可获得比模型三更快的速度.模型五是一个N P 问题,当点数较多时,甚至是不可能求解的.但本模型提供了一个较完美的具有理论意义的图论模型.312 对问题二的讨论11模型一:全局搜索法以某一个角度为步长转动网格,在每一角度下,固定网格方向按问题一的方法检验最多有多少旧井可以利用.再比较所有搜索过的角度下可利用的旧井数,即可得允许转动时可利用最多旧井数.两点间的棋盘距离会因转动而改变,故问题二采用欧氏距离.由于方格的对称性,只需从0°旋转到90°即可.为保证旋转小角度后,点的变动不超过精度Θ=0101,使步长∃Η≤ΘR ,R 为距离最远点到旋转中心的距离.本题中求出∃Η≤1104×10-3.需要将0,Π2分为2000份,因此本题要进行2000次问题一的计算.该模型简单可靠,易于理解,缺点是计算量较大,有很多不必要的搜索.因此有待改进.计算结果为:网格逆时针转动44137°,一个网格点在原坐标系下的坐标为(0147,0162).这时可有6个井被同时使用,井号为1,6,7,8,9,11.21模型二:旋转矢量法首先找两个可以同时利用的旧井,将这两旧井确定一个大致的方向,至多只能再转动一个极小的角度.在这个极小的角度内以步长∃Η转动,搜索最多可利用的旧井数.任意一对可同时利用的旧井都需要进行以上操作.定理21211 两旧井a ,b 可同时利用的充要条件为存在整数m ,n 使d -m 2+n 2≤2Ε,其中d =(a x -b x )2+(a y -b y )2为两旧井的欧氏距离.证明 (略)定理2.2.2 设两旧井a ,b 可同时被利用,a 点到网格原点距离d 1与b 点到结点(m ,n )距离d 2均不超过Ε.则当网格转动角度超过4Εd(其中d 为a 到b 的距离)弧度时,则d 1与d 2361期胡海洋等:钻井布局的数学模型中至少一个将超过Ε.证 因Ε<<d,以原点为旋转中心,将网格旋转∃Η弧度,b点相对结点(m,n)至少移动d∃Η,于是当∃Η>2Εd时,d2>Ε.同样以(m,n)为旋转中心,旋转∃Η2Εd时,d1>Ε.考虑最不利情形,当网格转动∃Η4Εd时,d1与d2中至少一个超过Ε.依据该定理,先将网格旋转与平移到某一位置,使a,b两旧井均被利用,在该位置,网格最多允许再旋转4Εd弧度.我们只需要在该小范围内检查其它井是否可被利用.对每一对井均作上述讨论,即可求得可利用的井数的最大值.31模型三:全局搜索 局部精化本模型的思想是先以较大步长进行全局搜索,找到一个大概范围,再在该范围内精确搜索,直至得到最优结果.将网格旋转某一角度Η(以弧度为单位),再将所有旧井按前文方法映射到原点周围四个单位网格内.现将误差扩大为Ε′=(1+∆)Ε,其中∆>0.作半径分别为Ε与Ε′的同心圆⊙与⊙′,使得⊙′内覆盖的映射点数最大,设为k′.若网格旋转角度有一个小的改变量∃Η,则各旧井在网格中的位置将移动R i∃Η,其中R i为第i号井到旋转中心的距离,此时它们的映射点也将移动R i∃Η距离.设R=m ax{R1,R2,…,R n},且R∃Η≤Ε′-Ε=∆Ε,即∃Η≤∆Ε R,(3)则原来在⊙′外的点不可能移入至⊙中(这是因为这两个同心圆边界的距离∆Ε大于映射点移动距离),于是当(3)成立时,⊙覆盖的映射点数k≤k′.基于上述分析,算法思想为:先取一适当的∆,以Ε′=(1+∆)Ε为允许误差,Θ=2∃Η=2∆Ε R为步长,从0到Π2进行搜索,求得可利用旧井数的上界M.将允许误差仍回到Ε,求得圆⊙覆盖的点数为m.若m=M,则可利用的旧井数就是M,问题已解决.若m< M,则适当减小∆,此时步长Θ也相应减小,进行精细搜索.搜索的范围可以减少很多.这是因为若对某一个角度Ηi,第一次以Ε′为允许误差求得的覆盖点数小于m,则显然旋转角度在区间[Ηi-∃Η,Ηi+∃Η]内时,可利用的点数也小于m,因此在第二次精细搜索时,该区间就不必检查了.从(3)可看出,若能减小R值,则在相同允许误差Ε′=(1+∆)Ε条件下,步长Θ=2∃Η将可增大,我们的做法是选择旋转中心,使得各旧井到旋转中心的最远距离最小,目标函数为f(x,y)=m ax1≤i≤n{(x i-x)2+(y i-y)2},s.t. m in f(x,y),其中(x,y)为新坐标原点(即旋转中心).这是非线性无约束最优规划问题,我们用SA S软件,采用单纯形法计算,结果为x= 5104,y=1170,R=f(x,y)=4155.此时R比以原坐标原点为旋转中心减少一半以上.我们取检查次数N=120,步长为90° 120=0175°.此时∆=ΠR4NΕ≈016,Ε′≈116Ε,得到可利用旧井的上界M=6.46数 学 的 实 践 与 认 识30卷另一方面,取任一步长,以半径为Ε的判决圆搜索可得到可利用旧井数的下界m .显然若上界与下界相等,则可利用的旧井数最多为m .而网格的方向就随之可确定.对于本题,步数取120,判决圆半径为Ε′=(1+∆)・Ε时,可得上界M =6.再取步数为2,判决圆半径为Ε时,步长为45度,得下界m =6.故可知最多可利用旧井数为6,旋转角度即为45度.仅需122次左右问题一的计算,可以较大的削减计算量.算法结果:可利用的旧井数的上限为6.网络逆时针旋转45°,其中一个节点坐标为(0146,0156),可利用旧井序号为(1,6,7,8,9,11).41对问题二各模型的评价模型一是直观和易于理解的,但搜索步数过多,耗时过长,模型二是先确定一个大致方向,再在该方向附近进行搜索.在n 较小时,可较大的削减计算量.但较大时,其确定的大致方向数过多,有可能得不偿失,反而增加计算复杂性.模型三我们认为是较好的,先以较大的步长搜索,再以小步长搜索,可以较大地减少计算量.313 问题三的解答在解决问题一、问题二的基础上,解决问题三.我们仅判断n 个点是否均可利用.11棋盘距离下因坐标旋转会改变两点间的棋盘距离,故只讨论网格不可旋转的情形.以某一口旧井为坐标原点建立平面直角坐标系,再将各旧井映射到以(-015,-015)与(015,015)为对角顶点的正方形内,即若旧井P i (i =1,2,…,n )的坐标为(x i ,y i ),它的映射象P ′i 的坐标(x ′i ,y ′i )满足(1)-015<x ′i ≤0.5,-0.5<y ′i ≤0.5;(2)x i -x ′i 与y i -y ′i 均为整数.显然我们有:定理3.1 记d x =m ax 1≤i <j ≤n {x i -x j },d y =m ax 1≤i <j ≤n{y i -y j },则在棋盘距离下n 口旧井均可利用的充要条件为d x ≤2Ε,d y ≤2Ε.21欧氏距离下网格不可旋转的情况同上述棋盘距离的映射方法,我们有:定理3.2.1 网络不可旋转的条件下,采用欧氏距离,n 口旧井均可利用的充要条件为它们的映射象P ′1,P ′2,…,P ′n 可被一判决圆所覆盖.适当移动判决圆,总可使该判决圆周上至少含两个映射点.据此,算法思想为:以任意两映射点确定两个半径为Ε的圆,检查是否所有的映射点均在判决圆上.最多检查2C 2n =n (n -1)次.算法的时间复杂度为O (n 3).我们还可给出欧氏距离下,不可旋转时n 口旧井均可利用的充分条件与必要条件:定理3.2.2 充分条件为任意两个映射象P ′i 与P ′j 的距离均不超过3Ε.证明 (略)定理3.2.3 必要条件为任意两个映射象P ′i 与P ′j 的距离均不超过2Ε.证明 (略)31欧氏距离下网格可旋转的情况561期胡海洋等:钻井布局的数学模型66数 学 的 实 践 与 认 识30卷选择一口旧井,使各旧井到它的最远距离最小,以这口井为坐标原点和旋转中心.设旋转了某一角度Η后,各井按旋转后的新坐标映射到以(-015,015)与(015,015)为对角顶点的正方形内,它们的映射象为P′i,i=1,2,…,n.则我们有定理3.3.1 存在一个角度Η∈[0,Π 2],使得旋转Η角后,各旧井的映射象P′1,P′2,…,P′n被一判决圆全部覆盖.计算可利用井数在问题二中已有详细讨论,我们建立的模型与算法均可用.例如由定理21211可知,若对两旧井a,b,不存在整数m,n,使得d-m2+n2≤2Ε成立,则a,b中最多只能利用一口井.因此该定理可作为判别n口井均可利用的一个必要条件.对于该问题,我们认为有效的一个充要条件是难找的,只有对实际问题进行求解计算来验证.4 模型结论改进方向及建议(略)参考文献:[1] 姜启源.数学模型1高等教育出版社,北京,1993.[2] 叶其孝1大学生数学建模竞赛辅导教材1湖南教育出版社,长沙,1997.[3] 朱道元1数学建模精品1东南大学出版社,南京,1999.The M athematical m odel of Borehole LayoutHU H ai2yang, CH EN J ian, LU X in(N an jing U n iversity,N an jing 210093)Abstract: In th is thesis,w e begin ou r research of m athem atical model of bo reho le layou t w ithan eye to the w ho le and then analyze step by step the effeciency,flex ib ility and comp lex ity of allk inds of calcu lating m ethods.A t last,w e get a relativity better m ethod to m ake ou t the num berof bo reho les that can be u tilized under differen t circum ferences.To the first questi on,after the demon strati on of an overall research model,p recise local model and a graph izalmodle,and after the discu ssi on of the flex ib ility and comp lex ity of vari ou scalcu lating m ethods,w e com e to the an s w er ram edy,that on ly fou r u sed bo redho les can be u ti2lized at mo st,num bered2,4,5,and10.To the second questi on,w e offer an overall research model,a p recise local model as w ell as a revo lving vecto r model.In particu lar,w e give a theo retical demon strati on of the localmod2 el.T he an s w er w e get is that on ly6u sed bo reho les can be u tilized at mo st,num bered1,6,7,8,9,and11and that the net w ill revo lve44137w ith a coo rdinate(0147,0167).To the th ird questi on,in o rder to judge w hether all of the given bo reho les can be u sed,w e enum erate the amp le requ irem en ts and the compu lso ry requ irem en ts together w ith the app ro ri2 ately effective calcu lating m ethod.。

海上丛式井组钻井顺序优化模型及求解方法曹向峰;管志川;史玉才;薛磊;张欣【摘要】海上丛式井组待钻井较多且井口间距较小,优化钻井顺序有助于防碰和采用批钻井方式.综合考虑防碰要求并兼顾批钻井要求,以井眼分离系数作为井眼交碰风险评价指标,以整个井组的防碰井段总长度最小作为钻井顺序优化目标,建立海上丛式井组钻井顺序优化模型及遗传算法求解方法,给出实例计算分析.结果表明:以整个井组的防碰井段总长度最小作为海上丛式井组钻井顺序优化指标是可行的;建立的钻井顺序优化方法能够满足海上丛式井防碰及批钻井要求.【期刊名称】《中国石油大学学报(自然科学版)》【年(卷),期】2016(040)003【总页数】6页(P96-101)【关键词】海上丛式井;钻井顺序;优化模型;防碰;批钻井;遗传算法【作者】曹向峰;管志川;史玉才;薛磊;张欣【作者单位】中国石油大学石油工程学院,山东青岛266580;中石化胜利石油工程有限公司钻井工艺研究院,山东东营257017;中国石油大学石油工程学院,山东青岛266580;中国石油大学石油工程学院,山东青岛266580;中国石油大学石油工程学院,山东青岛266580;中海油安全技术服务有限公司,天津300452【正文语种】中文【中图分类】TE21引用格式:曹向峰,管志川,史玉才,等.海上丛式井组钻井顺序优化模型及求解方法[J].中国石油大学学报(自然科学版),2016,40(3):96-101.海上丛式井组待钻井较多且井口间距较小,考虑防碰要求时通常先钻外围水平位移大、造斜点浅的井,后钻内排水平位移小、造斜点深的井[1-6];考虑批钻井要求时通常采用跳“日”字或“田”字的斜对角线钻井顺序[2]等。
笔者以防碰为优化目标,兼顾批钻井要求,建立海上丛式井组钻井顺序优化的数学规划模型及遗传算法求解方法。
防碰问题贯穿丛式井组钻井设计及施工全过程。
考虑到海上丛式井防碰问题的重要性,优选钻井顺序时应首先考虑防碰要求,其次才是批钻井要求。

井眼轨迹计算方法(一)井眼轨迹计算概述井眼轨迹计算是石油勘探和钻井工程领域中的重要技术之一。
它用于确定钻井孔的几何形状,以及记录井眼的位置和方向。
本文将介绍井眼轨迹计算的各种方法。
传统方法传统的井眼轨迹计算方法主要包括:1.平面梯形法:将井眼轨迹划分为一系列的小梯形,通过计算每个小梯形的底边和两侧斜边的长度,进而计算出井眼的轨迹。
2.立体三角法:将井眼轨迹划分为一系列的小三角形,通过计算每个小三角形的三条边的长度和夹角,进而计算出井眼的轨迹。
3.公式推导法:通过对井眼轨迹的方程进行推导和求解,得到井眼的位置和方向。
这种方法通常需要复杂的计算和数学推理。
传统方法的优点是可靠且易于理解,但缺点是计算量较大且需要繁琐的手工操作。
为了提高计算效率和精度,近年来出现了一些新的方法。
数值模拟方法数值模拟方法利用计算机对井眼轨迹进行模拟和计算。
常见的数值模拟方法包括:1.有限差分法:将井眼轨迹划分为一系列的井段,在每个井段上进行有限差分的计算,以得到井段的位置和方向。
这种方法可以实现高精度的计算,但需要较高的计算资源。
2.有限元法:将井眼轨迹的计算问题转化为一个边值问题,通过对问题的离散和求解,得到井眼的位置和方向。
有限元法可以适应各种复杂的井眼形状,但需要较长的计算时间。
3.其他方法:还有一些其他的数值模拟方法,如边界元法、神经网络等,它们采用不同的物理模型和计算算法,以求得更加准确和高效的井眼轨迹计算结果。
数值模拟方法的优点是计算速度快且精度高,但需要具备一定的计算机编程和数值计算的知识。
发展趋势随着计算机技术的发展和计算资源的提升,井眼轨迹计算方法也在不断演进。
未来,我们可以期待以下的发展趋势:1.算法优化:通过算法的优化和改进,提高计算速度和精度,降低计算资源的要求。
2.深度学习:利用深度学习等人工智能技术,从大量的井眼数据中学习和归纳规律,以实现更加准确和高效的井眼轨迹计算。
3.云计算:将井眼轨迹计算任务移至云端,在云计算平台上进行并行计算,以提高计算效率。
改进麻雀搜索算法优化支持向量机的井漏预测王鑫;张奇志【期刊名称】《科学技术与工程》【年(卷),期】2022(22)34【摘要】在钻井过程中,受地质环境、钻井技术等多种因素的影响,容易发生井漏事故。
为预防井漏事故,减少因钻井事故带来的损失,提出了一种改进麻雀搜索算法(improved sparrow search algorithm,ISSA)优化支持向量机的井漏预测方法。
首先,在发现者位置更新公式中引入一种改进的自适应非线性惯性递减权重,提高算法全局搜索能力;其次,在警戒者位置更新公式中引入莱维(Levy)飞行策略,减少算法陷入局部最优的风险。
为验证改进算法的寻优能力,将麻雀搜索算法(sparrow search algorithm,SSA)、遗传算法(genetic algorithm,GA)、灰狼算法(grey wolf algorithm,GWO)以及改进的麻雀搜索算法(ISSA)在8个基准测试函数上做了对比实验。
实验结果表明,改进的麻雀搜索算法(ISSA)在寻优精度、稳定性等方面都较其他算法更为优异。
最后,将改进的麻雀搜索算法用于优化支持向量机(ISSA-SVM)的惩罚参数C和核参数g,进行井漏事故的预测。
结果表明,ISSA-SVM 预测准确率为97.7654%,相比于麻雀算法(SSA)-SVM、遗传算法(GA)-SVM以及灰狼算法(GWO)-SVM预测准确率都高,且收敛速度快,迭代次数少,能够高效、快速预测井漏事故,提高钻井效率和可靠性。
【总页数】8页(P15115-15122)【作者】王鑫;张奇志【作者单位】西安石油大学电子工程学院;陕西省油气井重点测控实验室【正文语种】中文【中图分类】TE21【相关文献】1.基于麻雀搜索算法优化支持向量机的滚动轴承故障诊断2.基于麻雀搜索算法优化支持向量机的刀具磨损识别3.基于改进麻雀搜索算法优化支持向量机的短期光伏发电功率预测4.基于变分模态分解和混沌麻雀搜索算法优化支持向量机的滚动轴承故障诊断5.麻雀搜索算法优化BP神经网络的短期风功率预测因版权原因,仅展示原文概要,查看原文内容请购买。
钻井布局问题的算法
刘慧明;江守寰
【期刊名称】《青岛科技大学学报(自然科学版)》
【年(卷),期】2000(021)003
【摘要】讨论了勘探部门如何尽量利用旧井,少打新井以节省费用的问题.给出了求问题最优解的多种数值计算方法,并给出了所有旧井均可被利用的充分条件和必要条件.计算证明,上述算法是很有效的.
【总页数】5页(P248-252)
【作者】刘慧明;江守寰
【作者单位】青岛化工学院信息与控制工程学院,青岛,266042;青岛化工学院信息与控制工程学院,青岛,266042
【正文语种】中文
【中图分类】O242
【相关文献】
1.钻井布局问题 [J], 张斌武;秦榛
2.求解钻井布局问题的遗传算法 [J], 胡能发;文斌
3.基于偏序关系求解钻井布局问题的演化算法 [J], 胡能发;邓永发
4.基于偏序关系求解钻井布局问题的演化算法 [J], 胡能发;邓永发
5.钻井布局问题——99年全国大学生数学建模竞赛B题的一种解法 [J], 胡明因版权原因,仅展示原文概要,查看原文内容请购买。
钻井分布问题的优化摘要勘探部门在钻矿井的时候,要尽可能多地使用旧矿井。
在本文中,使用归一转化法与搜索法确定给出的矿井是否可以被再次利用。
探讨新的钻井应该如何布局才能尽可能多的利用旧钻井。
针对第一题,我们给出了归一转化模型、等效替代模型与搜索模型,确定在决定新井位置的网格可以横纵向移动时,可用的最大旧井数。
经过计算,得到当横纵向平移量分别为0.42和0.50时,可以利用的最大旧井数为4个,井号为2,4,5,10号。
针对第二题,在第一题的基础上,增加了网格可以旋转的条件,与问题一类似,对数据进行相同的归一转化与等效替代,在搜索的过程中加入新的网格变换条件,先旋转,再横纵向平移。
最后得到的可以被利用的旧井数为六个,旧井编号为1,6,7,8,9,11,对应的横纵向平移量和旋转量为0.47,0.62,44.37°。
针对第三题,建立等效模型,统一各个旧井点的参考结点。
在该模型下探讨旧井点应该满足怎样的条件才能使其全部利用。
得到的结论为:若旧井点经过等效变换后唯一一个以一个结点为圆心,判断误差值(0.05)为半径的圆中时,可以被全部利用。
利用问题二中得到的六个点进行特例验证,可以再一定程度上证明该判定条件的合理性。
关键词: 归一转换,等效映射,搜索1、问题重述及其建模准备:1.1背景在地质勘探过程中,要探明某个地区是否符合开采条件,在前期要实验性地布置勘探井来测试。
在经过初步测试后,会进一步地进行系统性的勘探。
在该勘探期间,要系统性地布置新的钻井,利用布置网格的方式来布置新的井位。
而钻一口新井相对于利用旧井花费是巨大的,所以如何设计整个网格系统来让旧井的利用率达到最高,则显得尤为重要。
1.2问题重述在某一地区,勘探人员已经先行打好了数口勘探井,为了进行进一步地勘探工作,需要再打一系列的勘探井来探明该地的储藏量。
为是新井的选取系统化,设计一个边长为单位一的正方形网格阵,每一个新的钻井都位于该网格阵的结点上,定义误差距离ε=0.05,规定若旧井和结点之间的距离小于等于该误差距离,则认为该旧井是可以利用的。
运筹学模型与数学建模竞赛一、引言一般来说,大学生数学建模竞赛所涉及到的运筹学模型涉及数学规划(线性规划和非线性规划),网络优化(含网络计划技术),排队模型,动态规划等,请看下表注:从1999年起,全国大学生数学建模竞赛开始设立专供大专院校学生做的C ,D 题。
下面重点介绍运筹学模型的数学规划。
二、数学规划的一般形式))(m ax ()(m in x f or x f⎪⎩⎪⎨⎧≤≤=≤==ub x lb m j x g li x h t s j i ,,2,1,0)(,,2,1,0)(.. 线性规划: 整数规划: 非线性规划:三、数学规划问题举例1 下料问题现要用100×50厘米的板料裁剪出规格分别为40×40 厘米与50×20厘米的零件,前者需要25件,后者需要30件。
问如何裁剪,才干最省料?解:先设计几个裁剪方案记 A---------40×40;B-----------50×20注:尚有别的方案吗?显然,若只用其中一个方案,都不是最省料的方法。
最佳方法应是三个方案的优化组合。
设方案i 使用原材料x i 件(i =1,2,3)。
共用原材料f 件。
则根据题意,可用如下数学式子表达:⎪⎩⎪⎨⎧=≥≥++≥+++=)3,2,1(03053252..min 32121321j x x x x x x t s x x x f j,整数 这是一个整数线性规划模型。
2 运送问题现要从两个仓库(发点)运送库存原棉来满足三个纺织厂(收点)的需要,数据如下表,方案1方案2方案3试问在保证各纺织厂的需求都得到满足的条件下应采用哪个运送方案,才干使总运费达成最小?(运价(元/吨)如下表)解:题意即要拟定从i 号仓库运到j 号工厂的原棉数量。
故设ij x 表达从i 号仓运到j 号工厂的原棉数量(吨)f 表达总运费.则运送模型为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥⎪⎭⎪⎬⎫=+=+=+⎭⎬⎫≤++≤+++++++=运输量非负约束;需求量约束运出量受存量约束),,j ,i (x x x x x x x x x x x x x .t .s x x x x x x f min ij 321210251540305042232231322122111232221131211232221131211 一般地,对于有m 个发点和n 个收点的运送模型为⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≥===≤=∑∑∑∑====),...2,1;,...2,1(0)...2,1(),...3,2,1(..min 1111n j m i x n j b x m i a x t s x c f ij mi j ij nj i ij m i nj ijij 其中a i 为i 号发点的运出量,b j 为j 号收点的需求量,c ij 为从i 号发点到j 号收点的单位运价。
钻井布局问题研究摘要本文主要研究了钻井布局过程中使可利用旧井位最大化的问题,即如何移动规划中的正方行网格(边长为1)使满足与网格结点的距离不超过个单位的旧井pi数最多。
文中先引入了0-1变量fi井可利用(与结点距离不超过0.05)fi为1,不可利用fi为0。
要进行了平行移动(不可旋转,只可横向、纵向移动)和自由移动(可旋转)的两方面研究。
在进行平行移动的研究中两点间的距离为其横向距离(横坐标之差的绝对值)及纵向距离(纵坐标之差的绝对值)的最大值。
自由移动的研究是在欧氏距离误差的意义下进行的。
在解决平移问题的过程中根据运动的相对性,文中将网格的移动转换成了旧井的整体移动。
对于问题一,然后假设旧井横向移动了x,纵向移动了y,用取整法求出旧井移动后离其最近的结点坐标。
,根据给定误差确定横向、纵向移动步长为0.01。
移动范围不超过1。
建立最优化模型,用Matlab搜索求解并画出点阵模型求出在平行移动的情况下可被利用的旧井最多4个,它们分别为:p2,p4,p5,p10。
对于问题二,网格除在纵向和横向方向移动之外,还进行旋转,我们把网格N以原点为中心先逆时针旋转θ度,再由横轴平移x单位,由纵轴平移y单位,根据条件我们确定旋转步长为1度,旋转范围(0,π∕),分析旧井点坐标,移动距离、旋转角度、移动后井点坐标、结点坐标的关系,建立最优化模型,再利用Matlab软件编写程序,用Matlab搜索求解并画出点阵模型,其能利用的旧井数量为7口。
对于问题三,由于问题二是相对于问题一的更优解,所以在网格二的基础上进行改动,以求得在何种旋转角度及何种平移距离下各旧井离最近网格的距离平方和最小。
在此种角度及平移条件下,求得各旧井离最近点的最大值,这个最大值就是新的距离条件,是能使旧井全部被利用到的距离条件的最小值。
关键词:0-1变量取整最优化模型 Matlab搜索求解1问题重述在平面上有n个井位ip,坐标为(ai,bi),现要重新布置井位,要求把新井布置在一个每个格子的边长都是1个单位的正方形网格N的所有结点(纵线和横线的交叉点)上。
第19卷第2期 怀化师专学报 V ol119N o12 2000年4月 J OURNA L OF HUAIHUA TEACHERS COLLEGE Apr.,2000钻井布局问题的搜索算法3蒲 飞, 龚玉龙, 吴齐峰, 宋燕霞(怀化师专数学系,湖南怀化 418008)摘 要:研究了钻井布局问题,采用将网格移动而井不动转化为井动而网不动的思想,对平移情形提出了两种搜索算法,一种是全程搜索,另一种是逐井优化搜索,并对后一种算法的有效性在理论上给出两个定理作保证1对旋转情形也采用全程搜索算法,并对所提算法进行了数值实验1通过比较,对平移情形,逐井优化搜索算法比全程搜索算法效率高得多,大大节省了搜索时间,且所得结果与全程搜索完全一致1最后,分别对所提算法的数值结果可视化1所给例子,求得只可平移时有4个旧井可利用,对可旋转又可平移的情况,求得有6个旧井可利用1关键词:平移;旋转;全程搜索;逐井优化搜索;参照井中图分类号:O241;T B115 文献标识码:A 文章编号:1007-1814(2000)02-0024-061 问题的提出勘探部门在某地区找矿,初步勘探时期已在若干位置钻井取得了地质资料,进入系统勘探时期后,要在一个区域内按纵横等距的网格点来布局井位,进行“撒网式”全面钻探1由于钻一口新井的费用很高,如果新设计的井位与原有井位重合(或相当接近),便可利用旧井的地质资料,不必打这口新井1因此,应该尽量利用旧井,少打新井,以节约钻探费用1设平面上有n个点P i,其坐标为(a i,b i),i=1,2,…,n,表示已有的n个井位1新布置的井位是一个正方形网格N的所有结点1假定每个格子的边长(井位的纵横间距)都是1单位1整个网格是可以在平面上任意移动的1若一个已知点P i与某个网格结点X i的距离不超过给定误差ε(=0105单位),则认为P i处的旧井资料可以利用,不必在结点X处打新井1为进行辅助决策,勘探部门提出如下问题:(1)假定网格的横向和纵向是固定的(比如东西向和南北向),并假定距离误差是沿横向和纵向计算的,即要求可利用井P i与相应的结点X i的横坐标之差(取绝对值)及纵坐标之差(取绝对值)均不超过ε1在平面上平行移动网格N,使可利用的旧井数尽可能多1试提供数值计算方法,并对下面的数值例子(表1)用计算机进行计算1(2)在问题(1)的基础上,考虑网格的横向和纵向不固定(可以旋转)的情形,给出算法及计算结果1表1 数值例子(n=12个点的坐标)i123456789101112a i015011413100313731404172417251437157813881899150b i2100315011503151515021006124411021014150314101802 模型假设及符号设置211 模型假设收稿日期:1999-10-223本文获1999年全国大学生数学建模竞赛三等奖1蒲飞为指导教师1作者简介:蒲飞(1970-),男,湖南洪江人,讲师,硕士,主要从事计算数学研究1(1)假设所考虑区域为平面区域1(2)不考虑井的大小,只把它当作平面上的点来处理1(3)假设利用旧井的费用远远小于钻一口新井的费用1(4)假设平移的方向为东西向和南北向1(5)旋转时旋转角度,以逆时针方向为正,顺时针方向为负1(6)网格的初始位置中有一条横线与X 轴重合,有一条纵线与Y 轴重合1212 符号设置:P i (a i ,b i ):第i 口旧井,其中(a i ,b i )为其坐标1X i :网格中的结点1ε:给定的误差,取为0105个单位1k :井纵向移动的单位数,k >0时向上移,k <0时向下移1h :井横向移动的单位数,h >0时向右移,h <0时向左移1[x ]:不超过x 的最大整数13 算法的分析及建立钻井布局实际上就是移动网格使尽可能多的结点与旧井的距离误差不超过ε,即可利用的旧井数尽可能地多1在网格移动的过程中,旧井的位置是不变的1为分析问题简单计,可看成是旧井动而网格不动的情形,则网格移动的方向实际上与旧井移动的方向相反1以下算法的设计均采用这一思想来处理1进一步,对平移情形可只考虑旧井横向与纵向的最大移动范围为1个单位的情形,若移动了x (x ≥1)个单位,各旧井移动后的位置与所在格子的四边的距离跟各旧井移动x —[x ](0≤x —[x ]<1)个单位时旧井位置与四边的距离完全一样1下面分别就只平移及平移且旋转两种情形来建立算法1311 只平移的情形31111 全程搜索算法:算法设计思想:由于给定的误差ε=0105单位,为保证搜索的精确度,取搜索步长为0101单位,做一个双重循环,外部循环做横向搜索,内部循环为纵向搜索,横向与纵向搜索范围均不超过1单位1每循环一次均搜索出可利用旧井数,搜索完毕后,求出最大可利用旧井数1算法:Step 1:输入旧井坐标1Step 2:作全程搜索,采用双重循环,h 1为横向搜索步长,h 2为纵向搜索步长1h 1从0开始,依次递增0101单位作外部循环,进行横向搜索,h 2从0开始,依次递增0101单位作内部循环1进行纵向搜索,依次计算各井与所在格子四个结点的横坐标之差(取绝对值)及纵坐标之差(取绝对值),若至少与一个结点的纵横坐标之差(取绝对值)均不超过ε,则认为此井可利用,可按下式计算:(1)与左下结点:a i -[a i ]≤ε,b i -[b i ]≤ε(2)与左上结点:a i -[a i ]≤ε,[b i ]+1-b i ≤ε(3)与右下结点:[a i ]+1-a i ≤ε,b i -[b i ]≤ε(4)与右上结点:[a i ]+1-a i ≤ε,[b i ]+1-b i ≤εStep 3:搜索完毕后,取可利用旧井数的最大值,并输出相应的横向、纵向平移长度,同时输出各旧井相应位置1数值计算结果:最大可利用井数为4,旧井向东移动016单位,向北移动015单位(即网格向西移动016单位,向南移动015单位)后各井位置如表2:・52・第19卷第2期 蒲飞等:钻井布局问题的搜索算法表2 只平移全程搜索算法的数值计算结果i 123456789101112a i 1110210131603197410051325132610381178198915810110b i215041002100410161002150617441602151510031911130 注:取得最大可利用井数时,移动方式不唯一131112 逐井优先搜索算法算法设计思想:由于全程搜索没有给出搜索的准则,运算量大,运行时间长,特别当结点数n 较大时,运算量巨大,因而在实际应用中并非好算法1若能找到搜索准则,则可大大降低运算量,减少运算时间1本算法先选参照井P 1,即把P 1移至所在格子四个结点中某一邻近区域(即与该结点横纵坐标之差的绝对值不超过ε的区域),其他结点平移方向同P 1,可通过如下定理1、定理2,计算出有多少个结点在平移后也被移至所在格对应结点邻近区域;然后依次选P 2,P 3,…,P n 为参照井,同样计算出各自可利用的井数;最后,取出最多可利用旧井数,设其对应的参照井为P k (1≤k ≤n ),找出可利用的旧井,给出平移方向1从而,由定理1、定理2可知,该方案即为更优方案1定理1 在n 个点P i (i =1,2,…,n )中任取一点,设为P 0(a 0,b 0),把它移至某一结点附近,即与纵横轴误差距离均不超于ε,若P i (a i ,b i )(P i ≠P 0)也被移至一结点附近,它们与纵横轴误差距离不超过ε,则有:a 0-[a 0]-2ε≤a i -[a i ]≤a 0-[a 0]+2εb 0-[b 0]-2ε≤b i -[b i ]≤b 0-[b 0]+2ε证明:如图1,点P 0可移至它邻近的四个结点1现取P 0右上方的结点考虑,其它三个结点可按同一方法处理1现P 0被移至它右上方的结点附近区域图1△0∶[[a 0]+1-ε,[a 0]+1+ε]×[[b 0]+1-ε,[b 0]+1+ε]则P i 也将被移至右上方1若P i 被移至a 0它右上方结点附近区域△i ∶[[a i ]+1-ε,[a i ]+1+ε]×[[b i ]+1-ε,[b i ]+1+ε] 设(a 0,b 0)被移至(a 0+h ,b 0+k ),h ,k ∈[0,1),有h ∈[[a 0]+1-a 0-ε,[a 0]+1-a 0+ε] (1)k ∈[[b 0]+1-b 0-ε,[b 0]+1-b 0+ε] (a i ,b i )被移到(a i +h ,b i +k )∈△i ,则h ,k 应满足h ∈[[a i ]+1-a i -ε,[a i ]+1-a i +ε] (2)k ∈[[b i ]+1-b i -ε,[b i ]+1-b i +ε]从图中可以看出,当h ,k 同时满足(1),(2)时,有:[a i ]+1-ε≤a i +[a 0]+1-a 0-ε≤[a i ]+1+ε[b i ]+1-ε≤b i +[b 0]+1-b 0-ε≤[b i ]+1+ε或[a i ]+1-ε≤a i +[a 0]+1-a 0+ε≤[a i ]+1+ε[b i ]+1-ε≤b i +[b 0]+1-b 0+ε≤[b i ]+1+ε或[a i ]+1-ε≤a i +[a 0]+1-a 0-ε≤[a i ]+1+ε[b i ]+1-ε≤b i +[b 0]+1-b 0+ε≤[b i ]+1+ε或・62・怀化师专学报 2000年4月[a i ]+1-ε≤a i +[a 0]+1-a 0+ε≤[a i ]+1+ε[b i ]+1-ε≤b i +[b 0]+1-b 0-ε≤[b i ]+1+ε解之得 a 0-[a 0]-2ε≤a i -[a i ]≤a 0-[a 0]+2ε b 0-[b 0]-2ε≤b i -[b i ]≤b 0-[b 0]+2ε 证毕定理2 若将井P 0(a 0,b 0)移至所在格子四个结点中任一结点邻近区域,即与该结点横纵坐标之差(取绝对值)均不超过ε的区域。
把P 0所在格子四个结点中任一结点的邻近区域划分为四个区域,如图2所示,对这样标记的四个区域,我们有以下结论:图2(1)若P 0进入区域1,则满足条件:a 0-[a 0]-ε≤a i -[a i ]≤a 0-[a 0]b 0-[b 0]-ε≤b i -[b i ]≤b 0-[b 0]的井P i (a i ,b i )必进入区域51(2)若P 0进入区域2,则满足条件:a 0-[a 0]≤a i -[a i ]≤a 0-[a 0]+εb 0-[b 0]-ε≤b i -[b i ]≤b 0-[b 0]的井P i (a i ,b i )必进入区域51(3)若P 0进入区域3,则满足条件:a 0-[a 0]≤a i -[a i ]≤a 0-[a 0]+εb 0-[b 0]≤b i -[b i ]≤b 0-[b 0]+ε的井P i (a i ,b i )必进入区域51(4)若P 0进入区域4,则满足条件:a 0-[a 0]-ε≤a i -[a i ]≤a 0-[a 0]b 0-[b 0]≤b i -[b i ]≤b 0-[b 0]+ε 的井P i (a i ,b i )必进入区域51证明:四种情形证明类似,这里只证明(1)1若P 0(a 0,b 0)进入区域1,设横向移动h ,纵向移动k 1则有:[a 0]+1≤a 0+h ≤[a 0]+1-ε [b 0]+1≤b 0+k ≤[b 0]+1+ε即有:[a 0]+1-a 0≤h ≤[a 0]+1+ε-a 0 [b 0]+1-b 0≤k ≤[b 0]+1+ε-b 0 则a i +[a 0]+1-a 0≤a i +h ≤a i +[a 0]+1-a 0+ε b i +[b 0]+1-b 0≤b i +k ≤b i +[b 0]+1-b 0+ε 又 a i +h =a i -[a i ]+[a i ]+h ≤a 0-[a 0]+[a i ]+[a 0]+1-a 0+ε=[a i ]+1+ε a i +h =a i -[a i ]+[a i ]+h ≥a 0-[a 0]+[a i ]+[a 0]+1-a 0-ε=[a i ]+1-ε即 [a i ]+1-ε≤a i +h ≤[a i ]+1+ε …(a ) 同样,b i +k =b i -[b i ]+[b i ]+k ≤b 0-[b 0]+[b 0]-b 0+ε+[b i ]=[b i ]+ε+1 b i +k =b i -[b i ]+[b i ]+k ≥[b i ]+b 0-[b 0]+[b 0]-b 0+1-ε=[b i ]+1-ε即 [b i ]+1-ε≤b i +k ≤[b i ]+ε+1 …(b )故由(1)、(2)得知,井P i (a i ,b i )必进入区域51算法:Step 1: F or Ⅰ=1 to n 选参照井P i (1≤i ≤n )计算满足条件:a i -[a i ]-2ε≤a j -[a j ]≤a i -[a i ]+2εb i -[b i ]-2ε≤b j -[b j ]≤b i -[b i ]+2ε (1)・72・第19卷第2期 蒲飞等:钻井布局问题的搜索算法的井P j (a j ,b j ),(j =1,2,…,n ,j ≠i )Step 2:a )将P i 平移至所在格子四个结点中任一结点的邻近区域1时,选取满足以下条件的所有井P j ,并统计其个数m 1:a i -[a i ]-ε≤a j -[a j ]≤a i -[a i ]b i -[b i ]-ε≤b j -[b j ]≤b i -[b i ] (2) b )将P i 平移至所在格子四个结点中任一结点的邻近区域2时,选取满足以下条件的所有井P j ,并统计其个数m 2:a i -[a i ]≤a j -[a j ]≤a i -[a i ]+εb i -[b i ]-ε≤b j -[b j ]≤b i -[b j ] (3) c )将P i 平移至所在格子四个结点中任一结点的邻近区域3时,选取满足以下条件的所有井P j ,并统计其个数m 3:a i -[a i ]≤a j -[a j ]≤a i -[a i ]+εb j -[b i ]≤b j -[b j ]≤b j -[b i ]+ε (4) d )将P i 平移至所在格子四个结点中任一结点的邻近区域4时,选取满足以下条件的所有井P j ,并统计其个数m 4:a i -[a i ]-ε≤a j -[a j ]≤a i -[a i ]b j -[b i ]≤b j -[b j ]≤b j -[b i ]+ε (5) e )对满足条件(1),但同时不满足条件(2),(3),(4),(5)的所有井P m ,分别计算当P i 平移至所在格子的四个结点中任一结点的邻近区域时,井P m 也被平移至所在格子四个结点中相应结点邻近区域的个数,取其最大者,记为m 5,设此时P i 被平移至结点X m 的邻近区域1Step 3:将井P i (a i ,b i )平移至X m 的邻近区域,计M i =m 1+m 2+m 3+m 4+m 5+1 (加1表示包含P i 本身)Step 4:若M k =max {M 1,M 2,……,M n },则将P k 移至X k 结点的邻近区域时可利用的旧井数最多,为M k 1数值计算结果:井向东移动0159个单位,向南移动0148个单位,最大可利用井数4个(见表3)1表3 只平移逐井优先搜索算法的数值计算结果i 123456789101112a i 1109210031593196319951315131610281168197915710109b i115231021102310051021152517631621153410221930132312 平移且可旋转情形全程搜索算法:算法设计思想:考虑到先平移后旋转与先旋转后平移是等价的,故采用先平移后旋转的搜索方法,搜索时为保证精确度,纵向步长与横向步长均取为0105单位,旋转角度为π/180,做三重循环,外部循环为横向搜索,中间循环为纵向搜索,内部循环为旋转搜索,横向与纵向搜索均不超过1单位1每循环一次均搜索出可利用旧井数,搜索完毕后,求出最大可利用旧井数1算法:step 1:输入旧井坐标,作全程搜索step 2:采用三重循环,h 1从0开始,依次递增0105单位,作为外部循环1k 1从0开始,依次递增0105单位,作为中间循环1θ从0开始依次递增π/180,作为内部循环,依次计算各井与所在格子四个结点的横坐标之差(取绝对值)及纵坐标之差(取绝对值)1若至少与一个结点的纵横轴坐标之差均不超过・82・怀化师专学报 2000年4月ε,则认为此井可利用1step 3:搜索完毕后取可利用旧井数的最大值,并比较出相应的横向平移长度,纵向平移长度以及旋转角度同时输出各旧井相应位置1数值计算结果:旋转角度为45度,水平移动0170个单位,上下移动0140个单位,最大可利用旧井数为6个(见表4)1表4 平移且可旋转全程搜索算法的数值计算结果i 123456789101112a i110001700141210431521198419831974100613451994151b i 201020140221142019801412310001002210225101231822510127113 注:取得最大可利用井时,旋转移动方式不唯一1算法的源程序因篇幅而没有附上,索要源程序请与作者联系1作者感谢数学系98级杨军、许任飞、计算机系98级陈鑫三位同学为本文所做的许多数值计算工作1参考文献:[1]张宜华1精通Matlab [M]1北京:清华大学出版社,19991[2]卢开澄1计算机算法导引———设计与分析[M]1北京:清华大学出版社,19981[3]张志涌1掌握和精通Matlab [M]1北京:北京航空航天大学出版社,19971Solving the Distribution Problem of Mine Via Search AlgorithmPU Fei , G ONG Y u 2long , W U Qi 2feng , S ONG Y ian 2xia(Department o f Mathematics ,Huaihua Teacher s ’College ,Huaihua ,Hunan 418008)Abstract :This paper considers the distribution problem of mine 1In the first case ,that parallel 2vertical m ovement of mesh is only permitted ,tw o search alg orithms are given 1One is called global search alg orithm ,the other is called optimal search alg orithm for each mine ,which efficiency is proved by tw o theorems 1In the second case ,the rotation of mesh is als o permitted ,the global search alg orithm is given 1All alg orithms are experienced by numeral experiment 1Through a giving ex 2am ple ,it shows that four mines can be used in the first case ,and six mines can be used in the second case 1K ey w ords :parallel 2vertical m ovement ;rotation ;global search ;optimal search for each mine ;referential mine・92・第19卷第2期 蒲飞等:钻井布局问题的搜索算法。