高中数学化归与转化的思想在解题中的应用

转化与化归思想在高中数学解题教学中的应用研究【摘要】：随着科技、经济的迅速发展,数学在不同领域的应用日益广泛,数学教育成为世界各国关注的重点。

数学思想方法是数学学科的精髓,是分析与解决问题的理论基础,而转化与化归思想是数学中最重要的思想之一。

数学解题过程中处处渗透着转化与化归思想,学生解题能力的高低很大程度上也取决于其转化与化归能力的强弱。

笔者身处高中一线教学,结合教育教学实践经验以及调查分析,发现目前高中生数学解题中的转化与化归能力相对欠缺,影响学生解题能力的提升。

笔者希望本文的研究能够给一线教师提供一定的借鉴作用,对于提高学生的解题能力提供一定的帮助。

首先,笔者通过文献参考,了解转化与化归思想在国内外的研究现状,分析转化与化归思想的本质和内涵、转化与化归的原则、以及高中数学解题中转化与化归的常用方法。

简单来说,转化与化归思想就是通过观察、分析、类比、联想等思维过程把数学中需要解决的问题,遵循熟悉化、简单化、直观化等原则,选择合适的方法进行转化,然后归结到某些已经解决或比较容易解决的问题的一种思想方法。

其次,通过访谈和调查问卷,以我校部分教师和学生为研究对象,分别从教师和学生的角度研究转化与化归思想在高中数学中的应用现状。

研究表明,目前高中教师能够认识到转化和化归思想在高中数学解题中的重要作用。

但是,不少教师本身对于转化与化归思想缺乏系统深入的研究,教学过程渗透有限。

大部分学生的转化与化归能力仍然有待提高。

然后,结合教学实践经验,从高中数学中的数列、立体几何、函数、解析几何以及不等式几个方面,分析转化与化归思想的渗透策略。

这里重点选取近几年高考试题中一些具有代表性的问题,结合学生解题过程中存在的问题,具体分析老师在教学过程中的处理方式以及实践效果。

并提供《常见的递推数列通项公式的求法》解题教学案例,对课堂实践情况进行了详细分析。

最后,结合调查研究,笔者提出几点教学建议。

一要相信学生,给他们更多实践的机会;二要深入挖掘教材,感悟化归思想;三要注重概念、定理、公式等基础知识的教学,并注重知识之间的联系;四是通过变式训练引导学生应用化归思想;五是加强一题多解和多解归一的训练;六是引导学生及时归纳总结。

化归思想在高中数学解题过程中的应用分析化归思想是高中数学解题中常用的一种方法，通过分析问题的特点，找到问题的本质，将复杂问题化为简单问题，从而更好地解决问题。

化归思想在高中数学解题中的应用非常广泛。

以代数与函数为例，化归思想可以用来解决方程与不等式的问题。

对于一元一次方程，我们可以通过变量的代换，将复杂的方程化为简单的线性方程，从而求解变量的值；对于一元二次方程，我们可以通过配方法，将其化为完全平方，并进行因式分解，从而求解变量的值。

同样，在不等式解题中，化归思想也非常有用。

我们可以通过变量的移项与配方法，将一元二次不等式化为完全平方不等式，从而求解变量的取值范围。

化归思想在几何解题中也有重要的应用。

在相似三角形的解题中，我们可以通过观察相似三角形的对应边比值的特点，将问题化简为类似的三角形问题，从而更好地求解相关角度或边长；在证明几何定理中，通过化归思想，可以将复杂的证明问题转化为简单的等价命题或已知定理的推论，从而简化证明过程，并提高证明的准确性和完整性。

化归思想在数列与数学归纳法的应用中也是非常重要的。

通过找到数列的通项公式，我们可以将数列的求和问题化为一元方程或求和公式的运算，从而得到数列的和；通过化归思想，我们可以将数学归纳法的问题化为一般命题的证明问题，从而更好地理解数学归纳法的原理与应用。

化归思想还可以在概率与统计等领域中发挥重要作用。

在概率问题中，通过化归思想，我们可以将复杂事件的概率计算问题化为简单事件的概率计算问题，从而更好地求解概率问题；在统计问题中，通过化归思想，我们可以将复杂的统计数据化简为简单的数据形式，从而更好地进行数据分析与统计推断。

化归思想在高中数学解题过程中是非常有效的方法。

通过将复杂问题化为简单问题，我们可以更好地理解问题的本质，更准确地解决问题。

化归思想的运用对于提高高中数学解题能力是非常重要的。

化归思想的运用也能够帮助学生培养逻辑思维能力，提高问题分析与解决问题的能力。

所谓化归思想方法，就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化，进而达到解决的一种方法。

在解决数学问题时，常遇到一些问题直接求解较为困难，需将原问题转化为一个新问题（相对来说，对自己较熟悉的），通过新问题的求解，达到解决原问题的目的，这就是转化的思想方法。

转化思想方法的特点是实现问题的规范化、模式化，以便应用已知的理论，方法和技巧达到问题的解决，其思维过程的形式如下图：转化具有多向性、层次性和重复性的特点。

为了实施有效的转化，既可以变更问题的条件，也可以变更问题的结论；既可以变换问题的内部结构，又可以变换问题的外部形式，这就是多向性，转化原则既可应用于沟通数学各分支学科的联系，从宏观上实现学科间的转化，又能调动各种方法与技术，从微观上解决多种具体问题，这是转化的层次性，而解决问题中可以多次地使用转化，使问题逐次达到规范化，这是转化原则应用的重复性。

转化思想方法包含三个基本要素：1、把什么东西转化，即转化的对象；2、转化到何处去，即转化的目标；3、如何进行转化，即转化的方法。

转化思想方法应遵循以下五条原则：1、熟悉化原则，将陌生的问题转化为熟悉的问题，以利于我们运用熟知的知识、经验和问题来解。

2、简单化原则，将复杂问题转化为简单的问题，通过对简单问题的解决，达到解决复杂问题的目的，或获得某种解题的启示和依据。

3、和谐化原则，转化问题的条件或结论，使其表现形式更符合数与形内部所表示和谐统一的形式，或者转化命题，使其推演有利于运用某种数学方法或符合人们的思维规律。

4、直观化原则，将比较抽象的问题转化为比较直观的问题来解决。

5、正难侧反原则，当问题正面讨论遇到困难时，应想到考虑问题的反面，设法从问题的反面去探求，使问题获得解决，或证明问题的可能性。

转化与化归思想在高中数学解题教学中的应用研究摘要：转化和化归思想是高中数学思想中很重要的一种思想，运用好转化和化归思想对于提高学生的数学思维能力和发展学生的数学应用意识都有很大的帮助。

掌握常见的转化与化归方法、运用原则和解题策略，以及思考如何提高转化与化归思想的运用能力，这些都是促进学生学习高中数学的重要因素。

关键词：转化与化归思想；高中数学；应用转化和化归思想简单来说就是在处理问题时，把待解决的问题，通过某种转化过程，归结为一类已经解决或者比较容易解决的问题，最终求解出原问题的思想方法。

转化和化归的目的是简化问题。

转化与化归思想从某种意义上来说培养了一种透过问题看本质的能力，促进学生运用已有的知识储备和缜密的思维去发现问题、转化问题，从而寻找更好的路线来解决问题。

转化与化归思想为各类问题的解决提供了不计其数的方法，以此可见掌握好转化与化归思想的意义重大。

在高中数学学习过程中熟练运用转化与化归思想，对于促进学生的数学学习是大有裨益的。

一、注重变量之间的转化与化归在高中数学中，各种变量和公式的运用都是比较开放的，这就需要学生全面掌握各个知识点，并达到灵活运用的程度，否则就会不断降低学生的学习效率，其问题也难以得到有效解决。

同时，学生还要找到问题的契合点，通过公式以及变量之间的转化和化归，以此来得到问题的最终答案。

如果满足了一定要求和条件，变量的值也可以作为常量来使用，这样就能使复杂的问题简单化，学生理解起来也比较容易。

对于问题的教学，以及数学转化与化归思想的学习，教师都要给予一定引导和帮助，尤其是在面对一些教学难点时，教师应该发挥自身的指导作用，帮助学生扫清障碍，从而实现数学变量之间的转化。

比如，在求不等式x2+px+1>2x+p恒成立的x的取值范围时，学生就可以利用变量之间的转换，把不等式看作是关于P的一次不等式，就能达到化繁为简的目的，问题的解决也会更加顺利。

高中阶段与函数有关的问题比较多，而且比初中和小学时期的知识更加复杂，更加难以理解，如果不通过转化与化归思想解决问题，会使其解决起来比较麻烦，也在一定程度上降低了学生的学习效率。

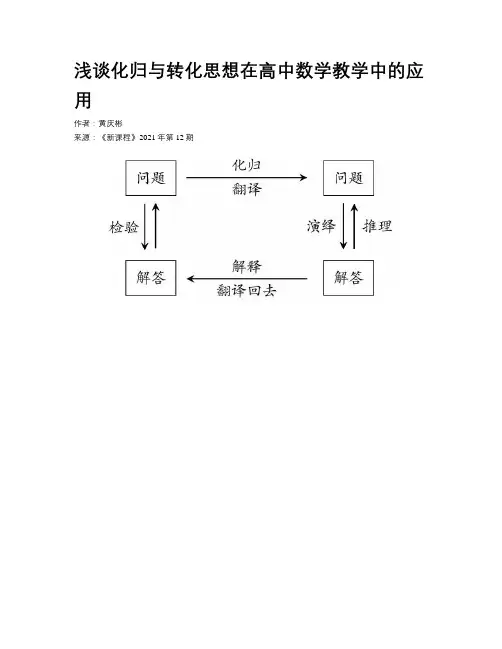
浅谈化归与转化思想在高中数学教学中的应用作者：黄庆彬来源：《新课程》2021年第12期新课程标准明确提出了高中生通过数学课程的学习要达到获“四基”、提“四能”的目标。

获“四基”，即学生获得数学基础知识、基本的技能、思想和活动经验;提“四能”，即提高学生从数学角度发现并提出问题、分析和解决问題的四种能力。

纵观近年来高考数学试题的编制及考查的内容，都很好地反映了课程改革理念，加大了数学思维能力的考查，注重学科思想方法的运用，这就要求教师在数学教学中要“两手抓”，既要加强基础知识与基本技能的教学，又要注意以素养为导向，以能力为重，加大各种思想方法的渗透。

在中学数学思想方法中，最基本、最核心的就是化归与转化思想，它是解决数学问题思想方法的精髓。

化归与转化，即运用转化、归结的数学手段，通过一定的数学过程，把一个复杂、陌生或者未解决的问题转化到已解决或较易解决的问题上来，从而破解原问题的一种方法。

数学家笛卡尔对此方法给予了高度评价，称之为解决数学问题的万能方法。

它对培养学生的解题能力和数学素质起至关重要的作用，故教师在平时教学中应注意引导学生抓基础与注重转化能力的培养两者并重，这是学好数学的金钥匙。

以下便是其模式。

一、高中数学中应用转化与化归思想遵循的原则应遵循4个原则：（1）熟悉化原则，即“化生为熟”，把陌生问题转化成熟悉问题。

（2）简单化原则，即“化繁为简”，把复杂问题转化成简单问题。

（3）直观化原则，即“化抽象为直观”，把较抽象的问题转化为较直观的问题（如数形结合思想，立体几何问题转化成平面几何问题）。

（4）正难则反原则。

若问题直接求解困难时，可考虑运用反证法或补集法，或用逆否命题间接地解决问题。

二、高中数学中常见的转化与化归方法共有10种：在解决数学问题时，有的可用直接转换法、换元法、数形结合法，有的可用参数法、构造法、坐标法，还有的可用类比法、特殊法、一般化、等价转换法来解。

这些方法在一些题目中可能单独使用，也可能相互交叉使用，是不能完全分割开的。

解题研究２０２３年１２月上半月㊀㊀㊀转化与化归 思想在高中数学解题教学中的应用◉哈尔滨师范大学教师教育学院㊀李㊀硕㊀㊀转化与化归 思想是高学数学中的一种重要的数学思想,运用非常广泛,尤其是一些特殊的问题,运用 转化与化归 思想解题可以提高效率,同时还可以降低问题解决的难度．因此,在数学课堂引入并应用转化与化归思想,能够让学生在学习数学及解题的过程中,加深对数学概念的理解,同时也能有效锻炼数学思维,提高学习效率,进一步发展数学核心素养．在高中数学的解题过程中,基于 转化与化归 思想的三大原则,主要运用的解题方法包括特殊与一般的转化㊁命题的等价转化,以及函数㊁方程㊁不等式之间的转化等一些常见的转化方法．１特殊与一般的转化将一般问题进行特殊化处理,可使问题的解决变得更为直接和简便,并且还能从特殊情况中寻找问题解决的常规思维;除此之外,对特殊性问题进行概括性研究,实现特殊问题一般化,也能从宏观与全局的角度把握特殊性问题的普遍规律,并能有效地解决特殊性问题．例１㊀ 蒙日圆 涉及几何学中的一个著名定理,该定理的内容为:椭圆上两条互相垂直的切线的交点必在一个与椭圆同心的圆上,该圆称为原椭圆的蒙日圆．若椭圆C :x ２a ＋１＋y ２a ＝１(a ＞０)的离心率为１２,则椭圆C 的蒙日圆的方程为(㊀㊀)．A．x ２＋y ２＝９㊀㊀㊀㊀㊀B ．x ２＋y ２＝７C ．x ２＋y ２＝５D．x ２＋y ２＝４分析:根据题目中的已知条件,在椭圆上,两条相互垂直的切线可以随意选择,但其交点位于与椭圆同心的圆却是唯一的,也即答案是唯一的．由此,可以通过选取一般问题的特殊情形找到一般的解题思路,不妨利用过椭圆的右顶点和上顶点的两条切线进行解题．解:因为椭圆C :x ２a ＋１＋y ２a＝１(a ＞０)的离心率为１２,所以１a ＋１＝１２,解得a ＝３．所以椭圆C 的方程为x ２４＋y ２３＝１,且椭圆C 的上顶点为A (０,３),右顶点为B (２,０),则椭圆在A ,B 两点的切线方程分别为y ＝３和x ＝２,这两条切线的交点坐标为M (２,３)．由题意可知,交点M 必在一个与椭圆C 同心的圆上,可得与椭圆C 同心的圆的半径r ＝２２＋(３)２＝７．所以椭圆C 的蒙日圆方程为x ２＋y ２＝７．故选:B ．以问题的特征为依据,对命题进行转化,将原问题转化为与之相关的㊁容易解决的新问题,这也是解决数学问题常见的转化思路,并且可以通过这种转化逐步培养识别关键信息的能力．２命题的等价转化把题目中已有的条件或者结论进行相应的转化,化难为易,是解决较难问题常用的转化手段．其主要方法包括:数与形的转化㊁正与反的转化㊁常量与变量的转化㊁图形形体及位置的转化等．例２㊀由命题 存在x ０ɪR ,使e |x －１|－m ɤ０是假命题,得m 的取值范围是(－ɕ,a ),则实数a 的值是．分析:利用转化思想可以将命题 存在x ０ɪR ,使e |x －１|－m ɤ０ 是假命题转化为 对任意x ɪR ,e|x －１|－m ＞０是真命题,由此得出m ＜e |x －１|恒成立,进而通过m 的取值范围来求a 的值．解:由命题 存在x ０ɪR ,使e |x －１|－m ɤ０是假命题,可知 对任意x ɪR ,e |x －１|－m ＞０是真命题,由此可得m 的取值范围是(－ɕ,１),而(－ɕ,a )与(－ɕ,１)为同一区间,故a ＝１．例３㊀若对于任意t ɪ[１,２],函数g (x )＝x ３＋(m ２＋２)x ２－２x 在区间(t ,３)上总不为单调函数,则实数m 的取值范围是．分析:根据函数g (x )＝x ３＋(m ２＋２)x ２－２x 在区间(t ,３)上总不为单调函数,可以利用正难则反的转化思想先找出g (x )在(t ,３)上单调的条件,再利用补集思想求出m 的取值范围．８５２０２３年１２月上半月㊀解题研究㊀㊀㊀㊀解:求得g ᶄ(x )＝３x ２＋(m ＋４)x －２．若g (x )在(t ,３)上单调递增,则g ᶄ(x )ȡ０,即３x ２＋(m ＋４)x －２ȡ０,亦即m ＋４ȡ２x－３x 在x ɪ(t ,３)上恒成立．故m ＋４ȡ２t－３t 在t ɪ[１,２]上恒成立,则m ＋４ȡ－１,即m ȡ－５．若g (x )在(t ,３)上单调递减,则g ᶄ(x )ɤ０,即m ＋４ɤ２x－３x 在x ɪ(t ,３)上恒成立,所以m ＋４ɤ２３－９,即m ɤ－３７３．综上,符合题意的m 的取值范围为－３７３＜m ＜－５．根据命题的等价性对题目条件进行明晰化处理是解题常见的思路;对复杂问题采用正难则反的转化思想,更有利于问题得到快速解答．３函数㊁方程㊁不等式之间的转化函数与方程㊁不等式之间有着千丝万缕的关联,通过结合函数y ＝f (x )图象可以确定方程f (x )＝０,不等式f (x )＞０和f (x )＜０的解集．例４㊀若２x －２y＜３－x －３－y ,则(㊀㊀)．A．l n (y －x ＋１)＞０B ．l n (y －x ＋１)＜０C ．l n |x －y |＞０D．l n |x －y |＜０分析:由题意,可将２x －２y＜３－x －３－y 转化为２x －３－x ＜２y－３－y ,进而实现不等式与函数之间的转化,从而解得答案．解:由２x －２y ＜３－x －３－y ,得２x －３－x ＜２y －３－y ．故构造函数y ＝２x －３－x ,即y ＝２x －(１３)x．由于函数y ＝２x－(１３)x 在R 上单调递增,因此x ＜y ,即y －x ＋１＞１．所以l n (y －x ＋１)＞l n １＝０．故选择:A ．例５㊀已知函数f (x )＝e l n x ,g (x )＝１ef (x )－(x ＋１)．(e ＝２．７１８ )(１)求函数g (x )的最大值;(２)求证:１＋１２＋１３＋ ＋１n ＞l n (n ＋１)(n ɪN ＋)．分析:第(１)问要求函数g (x )的最大值,关键在于需要运用转化与划归思想,通过g ᶄ(x )得出函数g (x )单调性,即可求出g (x )的最大值．将第(１)问得出的g (x )最大值－２转化成l n x －(x ＋１)ɤ－２,即l n x ɤx －１(当且仅当x ＝１时等号成立),再利用换元法最终证明出结论．解:(１)由g (x )＝１ef (x )－(x ＋１),即g (x )＝l n x －(x ＋１),得g ᶄ(x )＝１x－１(x ＞０)．令g ᶄ(x )＞０,则０＜x ＜１;令g ᶄ(x )＜０,则x ＞１．所以,函数g (x )在区间(０,１)上单调递增,在区间(１,＋ɕ)上单调递减．故g (x )的最大值为＝g (１)＝－２．(２)证明:由(１)知x ＝１是函数g (x )的极大值点,也是最大值点,故g (x )ɤg (１)＝－２．所以l n x －(x ＋１)ɤ－２,即l n x ɤx －１(当且仅当x ＝１时等号成立)．令t ＝x －１,则有t ȡl n (t ＋１)(t ＞－１)．取t ＝１n (n ɪN ＋),则有１n ＞l n (１＋１n)＝l n(n ＋１n )．故１＞l n２,１２＞l n ３２,１３＞l n ４３,,１n＞l n(n ＋１n )．上面n 个不等式叠加,得１＋１２＋１３＋ ＋１n＞l n (２ˑ３２ˑ４３ˑ ˑn ＋１n)＝l n (n ＋１)．故１＋１２＋１３＋ ＋１n ＞l n (n ＋１)(n ɪN ＋)．在分析此类题目的过程中,利用函数㊁方程㊁不等式进行转化与化归更有利于问题的解决,因此,利用转化与划归思想不仅能让整个数学知识的体系变得更加紧密,同时也能对学生从系统性角度掌握数学知识之间的联系提供非常大的帮助．转化与化归思想所蕴含的内容丰富且深奥,为高中数学问题的解决提供了多种思路,对高中数学的学习也有极大的指导与启发作用,值得我们不断地探索与研究．因此,在解决高中数学问题的过程中,要灵活运用 转化与化归 的解题思想．有些数学问题看似复杂,但通过分析可知出题者采用的是 障眼法 ,其中有的是多余或无用的条件．同时,在高中数学课堂教学中,教师可以在解题教学过程中渗透转化与化归思想,加强学生在特殊与一般转化㊁命题的等价转化以及函数㊁方程㊁不等式之间的转化等方面的技能,逐步锻炼学生简化题目内容的能力和意识,最大程度提高解题效率．Z９５。

GUAN ＧＤONG JIAO YU GAO ZHONG2021年第2化归与转化思想在高考数学解题中的运用■甘肃省秦安县第二中学罗文军yxo化归与转换的思想，就是在研究和解决数学问题时采用某种方式，借助某种函数性质、图像、公式或已知条件将问题通过变换加以转化，进而达到解决问题的思想等价转化总是将抽象转化为具体，复杂转化为简单、未知转化为已知，通过变换迅速而合理的寻找和选择问题解决的途径和方法.1．化归与转化的思想方法：解决数学问题时，常遇到一些问题直接求解较为困难，通过观察、分析、类比、联想等思维过程，选择运用恰当的数学方法进行变换，将原问题转化为一个新问题（相对来说，对自己较熟悉的问题），通过新问题的求解，达到解决原问题的目的.2．化归与转化应遵循的基本原则：（1）熟悉化原则；（2）简单化原则；（3）和谐化原则；（4）直观化原则；（5）正难则反原则3．化归与转化的途径：（1）从问题的反面思考；（2）局部向整体的转化；（3）未知向已知转化；（4）固定向重组的转化；（5）抽象向具体转化；（6）个别向一般的转化；（7）数向形的转化；（8）定量向定性的转化；（9）主元向辅元的转化.以下结合一些经典试题，谈谈化归与转化思想在高三解题中的运用.题型一：化归与转化思想简单化原则的体现化归与转化思想简单化原则在解题中的体现主要有：（1）将比较代数式的大小的问题，运用同构法，通过构造函数，化归为利用函数的单调性根据自变量的大小比较函数值的大小或者根据函数值的大小比较自变量的大小；（2）将概率与统计问题化归为集合间的基本关系与基本运算问题.例1.若2a +log 2a ＝4b +2log 4b ，则（）A.a ＞2b B.a ＜2b C.a ＞b 2 D.a ＜b 2【解析】由指数幂的运算性质和对数的运算性质可得，2a +log 2a ＝4b +2log 4b ＝22b +log 2b ，又因为22b +log 2b ＜22b +log 22b ＝22b +1+log 2b ，所以2a +log 2a ＜22b +log 22b .令ｆ（ｘ）＝2x +log 2ｘ，由指数函数和对数函数性质以及函数单调性的性质可得ｆ（ｘ）在（0，+∞）上单调递增，由ｆ（a ）＜ｆ（2a ），可得a ＜2b .【评析】本题考查了指数幂和对数的运算，函数的单调性的性质，构造函数后，把问题化归与转化为根据函数单调性，由函数值的大小比较自变量的大小，体现了化归与转化思想的简单化原则.例2.设命题p ∶4x-3≤1，命题q ∶x 2-（2a+1）x +a （a +1）≤0.若劭p 是劭q 的必要不充分条件，则实数a 的取值范围是__________.【解析】由4x-3≤1，得１２≤x ≤１，记A ＝{x │１２≤x ≤１}；由x ２-（２a+1）x+a （a+1）≤0，可得a ≤x ≤a +1，记B ＝{x │a ≤x ≤a +1}.因为劭p 是劭q 的必要不充分条件，所以q 是p 的必要不充分条件，所以p 是q 的充分不必要条件，所以A 芴B ，所以a ≤１２，a+１≥11，解得0≤a ≤１２，所以实数a 的取值范围是[0，１２].【评注】本题的解答中，先把两个命题中的不等式的解集分别用集合A 和集合B 表示，再由劭p 是劭q 是的必要不充分条件转化为p 是q 的充分不必要条件，再转化为集合A 为集合B 的真子集，解得a 的范围.题型二：化归与转化思想直观化原则的体现化归与转化思想直观化原则在解题中的体现主要有：（1）画出函数图像后，利用函数图像研究函数的性质，进而直观的解决与函数有关的问题；（2）立体几何问题中，将立体问题平面化，画出轴截面或者中截面，利用平面几何问题破解题目.例3.设a ，b ∈R ，则|“a ＞b ”是“a a ＞b b ”的（）A.充要不必要条件B.必要不充分条件C.充要条件D.既不充要也不必要条件【解析】构造函数ｆ（ｘ）＝x x ＝ｘ２，ｘ≥0-x ２，ｘ＜1函数图像如图1，由图像可知ｆ（ｘ）＝x x 在R 上单调递增.当a ＞b 时，ｆ（a ）＞ｆ（b ），即a a ＞b b ，a ＞b 圯a a ＞b b .当ｆ（a ）＞ｆ（b ），即a a ＞b b 时，a ＞b ，a a ＞b b 圯a ＞b ，所以a ＞b 圳a a ＞b b ，“a ＞b ”是“a a ＞b b ”的充要条件，故选C.【评注】本题是一道比较复杂的充分必要条件问题，通过观察题目，通过类比和联想，运用化归与转化思想，构造函数ｆ（ｘ）＝x x 后，画出这个函数的图像，运用图像法判断这个函数在其定义域R 上为单调递增函数，把a 和b 看成这个函数的两个自变量，a a 和b b 分别看成这个函数的函数值ｆ（a ）29数学有数和ｆ（b），由增函数的性质可以得出，ａ＞b圳a a＞b b，所以ａ＞b是a a＞b b的充分必要条件，体现了化归与转化思想的简单化和直观化原则.例4.已知某个机械零件是由两个有公共底面的圆锥组成的，且这两个圆锥有公共点的母线互相垂直，把这个机械零件打磨成球形，该球的半径最大为1，设这两个圆锥的高分别为h1，h２，则h1+h２的最小值为________．【答案】22姨.【解析】由题意可知，打磨后所得半径最大的球是由这两个圆锥构成的组合体的内切球，内切球的半径R=1，如图为这个组合体的轴截面示意图，圆O为内切球的轴截面，E，F，G，H分别为切点，连接OA，OB，OC，OD，OE，OF，OG，OH，由题意可知AB⊥BC，AD⊥DC，AC＝h1+h2，R＝OE＝OF＝OG＝OH＝1，则S四边形ABCD＝S△AOB+S△BOC+S△COD+S△AOD，即AB×BC＝１２R×AB+１２R×BC+１２R×CD+１２R×AD＝１２R（2AB+2BC）＝R（AB+BC），所以AB×BC＝AB+BC.由基本不等式可得AB×BC＝AB+BC≥2AB×BC姨，则AB×BC≥4，当且仅当AB＝BC时等号成立．所以（h1+h2）2＝AC2＝AB2+BC2≥2AB×BC≥8，当且仅当AB＝BC时等号成立，故h1+h2的最小值为22姨.【评注】本题的解答运用了化归与转化的思想，通过研究组合体和其内切球的轴截面，把空间立体几何问题化归为平面几何问题，做到了把问题直观化的原则.题型三：化归与转化思想熟悉化原则的体现化归与转化思想熟悉化原则在解题中的体现主要有：（1）不等式题目中，把含一个参数的不等式恒成立问题，通过分离变量，化归为求函数在给定区间上的最值问题；（2）立体几何题目中，利用长方体或者正方体模型，把一些三棱锥、四棱锥和三棱柱的外接球问题化归为熟悉的长方体或者正方体的外接球问题.例5.若对任意的ｘ∈（0，+∞），ax-ln（2ｘ）≥1恒成立，则实数a的最小值是_______【解析】由已知可得，对任意的ｘ∈（0，+∞），a≥ln（2ｘ）+1ｘ恒成立，令g（ｘ）＝ln（2ｘ）+1ｘ，g′（ｘ）＝１ｘ·ｘ-ln（2ｘ）ｘ2＝1-ln（2ｘ）ｘ2，令g′（ｘ）＝0，则1-ln（2ｘ）＝0，则ｘ＝e2，当0＜ｘ＜e2时，g′（ｘ）＞0，g（ｘ）单调递增；当ｘ＞e2时，g′（ｘ）＜0，g（ｘ）单调递减，所以当ｘ＝e2时，g（ｘ）取得最大值g（ｘ）max＝g（e2）＝ln e+1e2＝4e，所以a≥4e，所以a的最小值为4e.【评注】本题的解答运用了分离变量法，分离变量后，构造函数后，把a≥g（ｘ）在（0，+∞）上恒成立等价转化为a≥[g（ｘ）]max（ｘ∈（0，+∞）），转化为求函数g（ｘ）在（0，+∞）上的最大值问题，g（ｘ）的最大值即为a的最小值，本题体现了化归与转化思想的熟悉化原则.例6.设数列{a n}的前n项为S n，a1＝1，当n≥2时，a n＝2a n S n-2S2n.（1）求数列{a n}的通项公式；（2）是否存在正数k，使（1+S1）（1+S2）…（1+S n）≥k2n+1姨对一切正整数n都成立？若存在，求k的取值范围，若不存在，请说明理由.解：（1）因为当n≥2时，a n＝2a n S n-2S2n，所以a n＝2S2n2S n-1，n≥2，所以（S n-S n-1）（2S n-1）＝2S2n，所以S n-S n-1＝-2S n S n-1，所以１S n-１S n-1＝2，n≥2，所以数列{１S n}是以１S1＝1为首项，以2为公差的等差数列，所以１S n＝1+2（n-1）＝2n-1，所以S n＝１2n-1，所以，当n≥2时，a n＝S n-S n-1＝１2n-1-１2n-３＝-2（2n-1）（2n-3），因为a1＝S1＝1，所以a n＝1，n=1-2（2n-1）（2n-3）.n≥≥2（2）设ｆ（n）＝（1+S1）（1+S2）…（1+S n）2n+1姨，则ｆ（n+1）ｆ（n）＝2n+22n+1姨2n+3姨＝4n2+8n+44n2+8n+3姨＞1，所以ｆ（n）在n∈N鄢上递增，要使ｆ（n）≥k恒成立，只需要ｆ（n）min≥k，因为ｆ（n）min＝ｆ（1）＝2３姨３，所以0＜k≤2３姨3.【评注】第（1）问运用了数列的前n项和S n与通项a n之间的关系a n＝S n-S n-1（n≥2），把a n转化为S n-S n-1，再合并同类项后运用取倒数法，再根据等差数列的定义得出数列{１S n}的通项公式，再得出数列{a n}的通项公式；第（2）问分离变量后构造函数ｆ（n），用作商法判断ｆ（n）的单调性，把不等式ｆ（n）≥k在n∈N鄢上恒成立等价转化为ｆ（n）min≥k（n∈N鄢），两问都运用到了化归与转化思想.AEBFHDGOC302021年第2GUAN ＧＤONG JIAO YU GAO ZHONG2021年第2题型四：化归与转化思想和谐化原则的体现化归与转化思想和谐化原则在解题中的体现主要有：（1）解三角形问题中利用正弦定理实现边角的互化；（2）在三角函数问题中，将形如y=a sin x+b cos x 的函数问题利用辅助角公式化归为形如y=A sin （棕x+渍）的函数问题；（3）解析几何中，将两直线垂直化归为斜率乘积为-1或者方向向量的数量积为0；（4）将形如滋＝y -b x -a形式的最值问题，转化为动直线斜率的最值问题.例7.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b -c ＝a ·cos C -c ·cos A .（1）求角A ；（2）若a ＝3，求b +2c 的最大值.【解析】（1）因为b -c ＝a ·cos C -c ·cos A ，由正弦定理可得，sin B -sin C ＝sin A cos C -sin C cos A ，所以sin B -sin C ＝sin （A -C ）所以sin （A +C ）-sin C ＝sin （A -C ），所以sin A cos C +cos A sin C -sin C ＝sin A cos C -cos A sin C ，所以cos A ＝１２，因为0＜A ＜仔，所以A ＝仔３.（2）由（1）可得，C ＝２仔３-B ，由正弦定理得，a sin A ＝b sin B ＝c sin C＝2R ，所以３sin 仔３＝b sin B ＝c sin （２仔３-B ），所以b ＝2３姨sin B ，c ＝2３姨sin （２仔３-B ），所以b +2c ＝2３姨sin B +4３姨sin （２仔３-B ）＝2３姨（2sin B +３姨cos B ）＝221姨sin （B +渍），其中tan 渍＝３姨2，渍∈（0，仔2），由B ∈（0，２仔３），存在B 使得B +渍＝仔2，所以sin （B +渍）的最大值为1，所以b+２c 的最大值为221姨.【评注】第（1）问运用正弦定理实现边转化为角，再逆用两角差的正弦公式，运用内角和定理以及诱导公式，再运用两角和的正弦公式和两角差的正弦公式，得出cos A 的值，得出角A 的值；第（2）问运用了正弦定理将关于边的最值问题化为角的最值问题，运用三角形内角和定理以及诱导公式，再运用辅助角公式，化为三角函数在给定范围上的最值问题；两问都运用了化归与转化思想，体现了和谐化原则.例8.已知函数f （ｘ）＝ｘ2ｘ-1，则f （12019）+f （22019）+f （32019）+…+f （20182019）的值为_____.【解析】由于直接计算有困难，先探求一般的规律，因为f （ｘ）＝ｘ2ｘ-1，所以f （1-ｘ）＝1-ｘ2（1-ｘ）-1＝1-ｘ1-2ｘ＝ｘ-12ｘ-1，所以f （ｘ）+f （1-ｘ）＝1，倒叙相加可得f （12019）+f （22019）+f （32019）+…+f （20182019）＝1009.【评注】本题的解答中体现了特殊问题转化为一般化，运用了化归与转化思想，先通过探究在宏观上把握问题的一般规律，再将特殊问题破解.题型五：化归与转化思想的正难则反原则在解题中的体现化归与转化思想的正难则反原则在高中数学解题中的体现主要有：（1）间接证明方法中的反证法在解题中的运用；（2）概率问题中对立事件和互斥事件的概率公式的运用.例9.等差数列{a n }的前n 项和为S n ，a １＝1+2姨，S 3＝9+32姨.（1）求数列{a n }的通项a n 与前n 项和S n ；（2）设b n ＝S n n（n ∈N 鄢），求证：数列{b n }中任意不同的三项都不可能成为等比数列．【解析】（1）设公差为d ，由已知得ａ1＝2姨+1，3ａ1+3d ＝9+32姨姨，所以d ＝2，故a n ＝2n -1+2姨，S n ＝n （n +2姨）．（2）证明：由（1）得b n ＝S n n＝n +2姨.假设数列{b n }中存在三项b p 、b q 、b r （p 、q 、r 互不相等）成等比数列，则b 2q ＝b p b r ，即（q +2姨）2＝（p +2姨）（r +2姨），所以（q 2-pr ）+（2q -p-r ）2姨＝0.因为p ，q ，r ∈N 鄢，所以q ２-pr ＝0，2q-p-r ＝0姨，所以（p+r 2）２＝pr ，（p-r ）２＝0，所以p ＝r ，这与p ≠r 矛盾．所以数列{b n }中任意不同的三项都不可能成为等比数列.【评注】本题的解答的第（2）问中运用了反证法，先反设假定要证的结论不成立，而设出结论的反面成立，将这个反设作为条件，运用等比数列的定义和通项公式，通过推理，得出p ＝r 与已知条件相矛盾，所以反设错误，所以要证明的结论成立，反证法归属于间接证明方法，第（2）问运用了化归与转化的思想.例10.掷一个骰子的试验，事件A 表示“小于5的偶数点出现”，事件B 表示“小于5的点数出现”，则一次试验中，事件A +B 发生的概率为____.【答案】23.【解析】掷一个骰子的试验有6种可能结果，依题意P （A ）＝26＝13，P （B ）＝46＝23，所以P （B ）＝1-P （B ）＝1-23＝13，显然A 与B 互斥，从而P （A+B ）＝P （A ）+P （B ）＝13+13＝23.【评注】先由古典概型概率公式求出事件A 和事件B 的概率，再由对立事件概率公式求出事件B 的对立事件B 的概率，再由互斥事件概率公式，把事件A+B 的概率化归为求P （A ）和P （B ）的和，运用了化归与转化思想.责任编辑徐国坚31。