编译原理第三章自动机基础(1)资料
- 格式:ppt
- 大小:1.09 MB
- 文档页数:21






第三章习题参考解答3.1 构造自动机A,使得①②③当从左至右读入二进制数时,它能识别出读入的奇数;④它识别字母表{a, b}上的符号串,但符号串不能含两个相邻的a,也不含两个相邻的b;⑤它能接受字母表{0, 1}上的符号串,这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数,其中,d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA:① xy*∣yx*y∣xyx;② 00∣(01)*∣11;③ 01((10∣01)*(11∣00))*01;④ a(ab*∣ba*)*b。
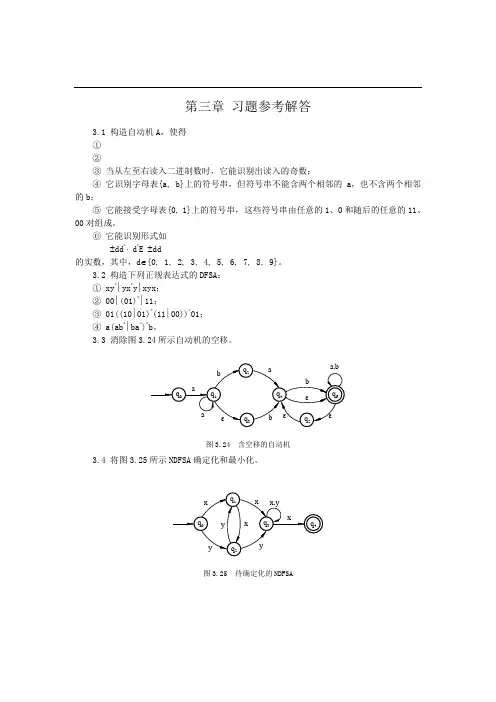
3.3 消除图3.24所示自动机的空移。
bεq1q2q3aba,bqaq6q4q5abεεε图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
xyqq1q2q4q3xyxyx,yx图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式,试证明① e∣e=e;② {{e}}={e};③ {e}=ε∣e{e};④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机,指明该自动机是不是确定的,并写出它相应的语言: G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中,f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA确定化。
3.8 设文法G[〈单词〉]:〈单词〉→〈标识符〉∣〈无符号整数〉〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉〈字母〉→a∣b〈数字〉→1∣2试写出相应的有限自动机和状态图。

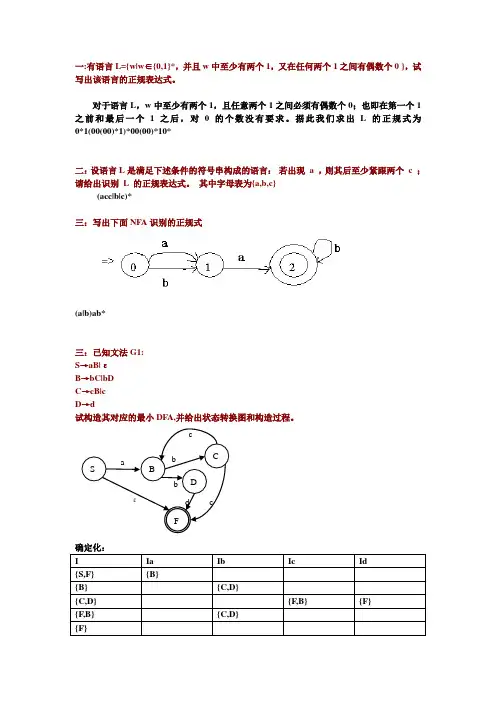
一:有语言L={w|w∈{0,1}*,并且w中至少有两个1,又在任何两个1之间有偶数个0 },试写出该语言的正规表达式。
对于语言L,w中至少有两个1,且任意两个1之间必须有偶数个0;也即在第一个1之前和最后一个1之后,对0的个数没有要求。
据此我们求出L的正规式为0*1(00(00)*1)*00(00)*10*二:设语言L是满足下述条件的符号串构成的语言:若出现 a ,则其后至少紧跟两个 c ;请给出识别L 的正规表达式。
其中字母表为{a,b,c}(acc|b|c)*三:写出下面NFA识别的正规式(a|b)ab*三:已知文法G1:S→aB|εB→bC|bDC→cB|cD→d试构造其对应的最小DFA,并给出状态转换图和构造过程。
确定化:最小化:{1,5,4} {2,3} {1}{5}{4}{2}{3} 上图即为最小DFA四:设有L(G)={a 2n+1b 2m a 2p+1| n ≥0,p ≥0,m ≥1}。
(1) 给出描述该语言的正规表达式; (2) 构造识别该语言的确定有限自动机(可直接用状态图形式给出)并化简。
该语言对应的正规表达式为a(aa)*bb(bb)*a(aa)*,正规表达式对应的NFA 如图:确定化:(按照定义,上图已经是DFA ,所以下面确定化不做也是可以的,直接最小化)由最小化方法得到 {0,2} {1} {3,5} {4,6} {7} 最简的DFA :a重新命名五: 将图所示的非确定有限自动机(NFA)变换成等价的确定有限自动机(DFA)并化简。
其中,X 为初态,Y 为终态。
然后根据最小DFA ,写出对应的正规文法(右线性)b重新命名A->aB|bCB->aF|a|bE|b C->bDD->aD|bF|b E->aF|a|bD F->aF|bF|a|b。

编译原理第3章内容简介学习目标第3章有穷自动机3.1 有穷自动机的形式定义3.1 有穷自动机的形式定义DFA的表示举例——状态转换表DFA的表示举例——状态转换图 3.13.1 FA的形式定义有穷自动机识别的符号串举例DFA A3.1 有穷自动机的形式定义 3.1 有穷自动机的形式定义NFA举例 3.13.1用NFA识别符号串yFA的构造FA的构造举例—1FA的构造举例—2FA的构造举例—3请构造一个有穷自动机FA的构造举例—4 3.1请构造一个有穷自动机FA的等价性举例3.2 NFA到DFA的转换 3.2 NFA到DFA的转换—NFA确定化3.2 NFA到DFA的转换3.2 NFA到DFA的转换—NFA确定化——ε闭包状态子集I的ε闭包——举例状态子集I的状态子集I的ε闭包——举例状态子集I的——Ia 子集3.2 NFA到DFA的转换Ia子集——举例Ia子集——举例 3.2 NFA到DFA的转换NFA到DFA的转换——子集法NFA=(Q NFA到DFA的转换——举例1aNFA到DFA的转换——举例2NFA DFA DFA NFA DFA DFADFA化简举例1DFA化简——注意NFA到最小化DFA的转换——举例33.3 正规文法与FA3.3 正规文法与FAFA⇒右线性正规文法FA⇒右线性正规文法——举例1y3.4 正规表达式RE与FA 正规表达式与有穷自动机3.4 RE与FA——RE的性质 3.4 RE与FA—RE⇒FARE⇒FA举例1RE⇒FA举例23.4 RE与FA——FA⇒RE FA⇒REFA⇒RE FA⇒RE举例FA⇒RE举例正规文法到正规表达式正规文法到正规表达式DFA的程序实现DFADFA的程序实现DFA DFA的程序实现lDFA的程序实现l第3章内容小结第3章内容小结参考文献。