工程热力学 理想气体供参习

第4章 理想气体热力过程及气体压缩4．1 本章基本要求熟练掌握定容、定压、定温、绝热、多变过程中状态参数p 、v 、T 、∆u 、∆h 、∆s 的计算，过程量Q 、W 的计算，以及上述过程在p -v 、T -s 图上的表示。

4．2 本章重点结合热力学第一定律，计算四个基本热力过程、多变过程中的状态参数和过程参数及在p -v 、T -s 图上表示。

本章的学习应以多做练习题为主，并一定注意要在求出结果后，在p -v 、T -s 图上进行检验。

4．3 例 题例1．2kg 空气分别经过定温膨胀和绝热膨胀的可逆过程，如图4.1，从初态1p =9.807bar,1t =300C ο膨胀到终态容积为初态容积的5倍，试计算不同过程中空气的终态参数，对外所做的功和交换的热量以及过程中内能、焓、熵的变化量。

图4.1解：将空气取作闭口系对可逆定温过程1-2，由过程中的参数关系，得bar v v p p 961.151807.92112=⨯==按理想气体状态方程，得111p RT v ==0.1677kg m /3 125v v ==0.8385kg m /312T T ==573K 2t =300C ο气体对外作的膨胀功及交换的热量为1211lnV V V p Q W T T ===529.4kJ 过程中内能、焓、熵的变化量为12U ∆=0 12H ∆=0 12S ∆=1T Q T=0.9239kJ /K 或12S ∆=mRln12V V =0.9238kJ /K 对可逆绝热过程1-2′, 由可逆绝热过程参数间关系可得kv v p p )(211'2= 其中22'v v ==0.8385kg m /3 故 4.12)51(807.9'=p =1.03barRv p T '''222==301K '2t =28C ο气体对外所做的功及交换的热量为)(11)(11'212211T T mR k V p V p k W s --=--==390.3kJ 0'=s Q过程中内能、焓、熵的变化量为kJ T T mc U v 1.390)(1212''-=-=∆或kJ W U 3.390212'-=-=∆kJ T T mc H p 2.546)(1212''-=-=∆ '12S ∆=0例2. 1kg 空气多变过程中吸取41.87kJ 的热量时，将使其容积增大10倍，压力降低8倍，求：过程中空气的内能变化量，空气对外所做的膨胀功及技术功。

第2章理想气体的性质2.1 本章基本要求熟练掌握理想气体状态方程的各种表述形式，并能熟练应用理想气体状态方程及理想气体定值比热进行各种热力计算。

并掌握理想气体平均比热的概念和计算方法。

理解混合气体性质，掌握混合气体分压力、分容积的概念。

2.2 本章难点1．运用理想气体状态方程确定气体的数量和体积等，需特别注意有关物理量的含义及单位的选取。

2．考虑比热随温度变化后，产生了多种计算理想气体热力参数变化量的方法，要熟练地掌握和运用这些方法，必须多加练习才能达到目的。

3．在非定值比热情况下,理想气体内能、焓变化量的计算方法，理想混合气体的分量表示法，理想混合气体相对分子质量和气体常数的计算。

2.3 例题例1：一氧气瓶内装有氧气，瓶上装有压力表，若氧气瓶内的容积为已知，能否算出氧气的质量。

解：能算出氧气的质量。

因为氧气是理想气体，满足理想气体状态方程式mRTPV 。

根据瓶上压力表的读数和当地大气压力，可算出氧气的绝对压力P，氧气瓶的温度即为大气的温度；氧气的气体常数为已知；所以根据理想气体状态方程式，即可求得氧气瓶内氧气的质量。

例2：夏天，自行车在被晒得很热的马路上行驶时，为何容易引起轮胎爆破？解：夏天自行车在被晒得很热的马路上行驶时，轮胎内的气体（空气）被加热，温度升高，而轮胎的体积几乎不变，所以气体容积保持不变，轮胎内气体的质量为定值，其可视为理想气体，根据理想气体状态方程式mRT PV =可知，轮胎内气体的压力升高，即气体作用在轮胎上的力增加，故轮胎就容易爆破。

例3：容器内盛有一定量的理想气体，如果将气体放出一部分后达到了新的平衡状态，问放气前、后两个平衡状态之间参数能否按状态方程表示为下列形式：（a ）222111T v P T v P = （b ）222111T V P T V P = 解：放气前、后两个平衡状态之间参数能按方程式（a ）形式描述，不能用方程式（b ）描述，因为容器中所盛有一定量的理想气体当将气体放出一部分后，其前、后质量发生了变化，根据1111RT m v p =，2222RT m v p =，而21m m ≠可证。

江苏科技大学《工程热力学》练习题参照答案第一单元一、判断正误并说明原因：1.给理想气体加热，其热力学能老是增添的。

错。

理想气体的热力学能是温度的单值函数，假如理想气体是定温吸热，那么其热力学能不变。

1.丈量容器中气体压力的压力表读数发生变化必定是气体热力状态发生了变化。

错。

压力表读数等于容器中气体的压力加上大气压力。

所以压力表读数发生变化能够是气体的发生了变化，也能够是大气压力发生了变化。

2.在张口系统中，当进、出口截面状态参数不变时，而单位时间内流入与流出的质量相等，单位时间内互换的热量与功量不变，则该系统处在均衡状态。

错。

系统处在稳固状态，而均衡状态要求在没有外界影响的前提下，系统在长时间内不发生任何变化。

3.热力系统经过随意可逆过程后，终态 B的比容为 v B大于初态 A 的比容 v A，外界必定获取了技术功。

错。

外界获取的技术功能够是正，、零或负。

4.在朗肯循环基础上推行再热，能够提升循环热效率。

错。

在郎肯循环基础上推行再热的主要利处是能够提升乏汽的干度，假如中间压力选的过低，会使热效率降低。

6．水蒸汽的定温过程中，加入的热量等于膨胀功。

错。

因为水蒸汽的热力学能不是温度的单值函数，所以水蒸汽的定温过程中，加入的热量其实不是所有用与膨胀做功，还使水蒸汽的热力学能增添。

7．余隙容积是必要的但又是有害的，设计压气机的时候应尽可能降低余隙比。

对。

余隙容积的存在降低了容积效率，防止了活塞随和门缸头的碰撞，保证了设施正常运行，设计压气机的时候应尽可能降低余容比。

8．内燃机定容加热理想循环热效率比混淆加热理想循环热效率高。

错。

在循环增压比同样吸热量同样的状况下，定容加热理想循环热效率比混淆加热理想循环热效率高；但是在循环最高压力和最高温度同样时，定容加热理想循环热效率比混淆加热理想循环热效率低。

9．不行逆过程工质的熵老是增添的，而可逆过程工质的熵老是不变的。

错。

熵是状态参数，工质熵的变化量仅与初始和终了状态有关，而与过程可逆不可逆没关。

第四章 理想气体的性质第一节 理想气体的概念热能转变为机械能通常是借助于工质在热动力设备中的吸热、膨胀作功等状态变化过程而实现的。

为了分析研究和计算工质进行这些过程时的吸热量和作功量，除了以热力学第一定律为主要的基础和工具外，还需具备工质热力性质方面的知识。

热能转变为机械能只能通过工质膨胀作功实现，采用的工质应具有显著的涨缩能力,即其体积随温度、压力能有较大的变化。

物质的三态中只有气态具有这一特性，因而热机工质一般采用气态物质，且视其距液态的远近又分为气体和蒸气。

气态物质的分子持续不断地做无规则的热运动，分子数目又如此的巨大，因而运动在任何一个方向上都没有显著的优势，宏观上表现为各向同性，压力各处各向相同，密度一致。

自然界中的气体分子本身有一定的体积，分子相互间存在作用力，分子在两次碰撞之间进行的是非直线运动，很难精确描述和确定其复杂的运动，为了方便分析、简化计算,引出了理想气体的概念。

理想气体是一种实际上不存在的假想气体，其分子是些弹性的、不具体积的质点，分子间相互没有作用力。

在这两点假设条件下，气体分子的运动规律极大地简化了，分子两次碰撞之间为直线运动，且弹性碰撞无动能损失。

对此简化了的物理模型，不但可定性地分析气体某些热力学现象，而且可定量地导出状态参数间存在的简单函数关系。

众所周知，高温、低压的气体密度小、比体积大,若大到分子本身体积远小于其活动空间，分子间平均距离远到作用力极其微弱的状态就很接近理想气体。

因此，理想气体是气体压力趋近于零(p →0)、比体积趋近于无穷大(v →∞)时的极限状态。

一般来说，氩、氖、氦、氢、氧、氮、一氧化碳等临界温度低(参见附表2)的单原子或双原子气体，在温度不太低、压力不太高时均远离液态，接近理想气体假设条件。

因而，工程中常用的氧气、氮气、氢气、一氧化碳等及其混合空气、燃气、烟气等工质,在通常使用的温度、压力下都可作为理想气体处理，误差一般都在工程计算允许的精度范围之内。

工程热力学课后习题答案工程热力学课后习题答案热力学是工程学中的重要分支，它研究能量转化和传递的规律。

在学习热力学的过程中，课后习题是检验学习成果和巩固知识的重要途径。

下面将为大家提供一些工程热力学课后习题的详细解答，希望能对大家的学习有所帮助。

1. 一个理想气体在等压条件下，从体积为1m³压缩到0.5m³，压力保持不变。

求气体对外界做功的大小。

解答：根据理想气体的等压过程，气体对外界做功的大小等于压力乘以体积的变化量。

即W = PΔV = P(V2 - V1) = P(0.5m³ - 1m³) = -0.5Pm³。

2. 一个系统的内能增加了1000J，同时对外界做了500J的功。

求系统所吸收的热量。

解答：根据能量守恒定律，系统吸收的热量等于内能增加量与对外界所做功的和。

即Q = ΔU + W = 1000J + 500J = 1500J。

3. 一个容器内有1kg的水，初始温度为20℃。

将容器放在恒温室内，经过一段时间后，水的温度升至30℃。

求水所吸收的热量。

解答：根据热容公式Q = mcΔT，其中 Q 表示吸收的热量，m 表示物体的质量，c 表示物体的比热容，ΔT 表示温度的变化量。

将题目中的数据代入公式，即 Q= 1kg × 4186J/kg℃ × (30℃ - 20℃) = 41860J。

4. 一个活塞与一个理想气体接触，气体的初始体积为1m³，初始压力为2MPa。

经过一定过程后，气体的体积减小到0.5m³，压力增加到4MPa。

求气体对外界做的功。

解答：根据理想气体的等压过程，气体对外界做的功等于压力乘以体积的变化量。

即W = PΔV = P(V2 - V1) = 4MPa × (0.5m³ - 1m³) = -2MJ。

5. 一个系统的内能增加了2000J，同时对外界做了1000J的功。

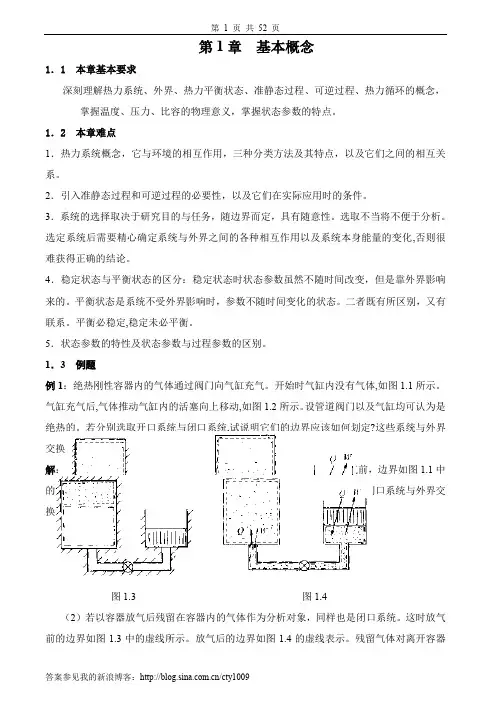
第1章基本概念1．1 本章基本要求深刻理解热力系统、外界、热力平衡状态、准静态过程、可逆过程、热力循环的概念，掌握温度、压力、比容的物理意义，掌握状态参数的特点。

1．2 本章难点1．热力系统概念，它与环境的相互作用，三种分类方法及其特点，以及它们之间的相互关系。

2．引入准静态过程和可逆过程的必要性，以及它们在实际应用时的条件。

3．系统的选择取决于研究目的与任务，随边界而定，具有随意性。

选取不当将不便于分析。

选定系统后需要精心确定系统与外界之间的各种相互作用以及系统本身能量的变化,否则很难获得正确的结论。

4．稳定状态与平衡状态的区分：稳定状态时状态参数虽然不随时间改变，但是靠外界影响来的。

平衡状态是系统不受外界影响时，参数不随时间变化的状态。

二者既有所区别，又有联系。

平衡必稳定,稳定未必平衡。

5．状态参数的特性及状态参数与过程参数的区别。

1．3 例题例1：绝热刚性容器内的气体通过阀门向气缸充气。

开始时气缸内没有气体,如图1.1所示。

气缸充气后,气体推动气缸内的活塞向上移动,如图1.2所示。

设管道阀门以及气缸均可认为是绝热的。

若分别选取开口系统与闭口系统,试说明它们的边界应该如何划定?这些系统与外界交换的功量与热量又如何?解：(1)若以容器内原有的气体作为分析对象，属于闭口系统。

容器放气前，边界如图1.1中的虚线所示。

放气后边界如图1.2中的虚线所示。

气体对活塞作的功W是闭口系统与外界交换的功量。

气体通过活塞与外界交换的热量Q是此闭口系统的传热量。

图1.1 图1.2图1.3 图1.4（2）若以容器放气后残留在容器内的气体作为分析对象，同样也是闭口系统。

这时放气前的边界如图1.3中的虚线所示。

放气后的边界如图1.4的虚线表示。

残留气体对离开容器的那部分放逸气体所作的功，是本闭口系统与外界交换的功，残留气体与放逸气体之间交换的热量是本系统的传热量。

（3）类似地若以放逸气体为分析对象，同样也是闭口系统。

其边界将如图1.3和图1.4中的点划线所示。

工程热力学（第五版）第6章.水蒸气练习题供参习第6章水蒸汽7．1 本章基本要求理解水蒸汽的产生过程，掌握水蒸汽状态参数的计算，学会查水蒸汽图表和正确使用水蒸汽h -s 图。

掌握水蒸汽热力过程、功量、热量和状态参数的计算方法。

自学水蒸汽基本热力过程(§7-4)。

7．2 本章难点1．水蒸汽是实际气体，前面章节中适用于理想气体的计算公式，对于水蒸汽不能适用，水蒸汽状态参数的计算，只能使用水蒸汽图表和水蒸汽h-s 图。

2．理想气体的内能、焓只是温度的函数,而实际气体的内能、焓则和温度及压力都有关。

3．查水蒸汽h -s 图，要注意各热力学状态参数的单位。

7．3 例题例1：容积为0.63m 的密闭容器内盛有压力为3.6bar 的干饱和蒸汽，问蒸汽的质量为多少，若对蒸汽进行冷却，当压力降低到2bar 时，问蒸汽的干度为多少，冷却过程中由蒸汽向外传出的热量为多少解：查以压力为序的饱和蒸汽表得：1p =3.6bar 时，"1v =0.51056kg m /3 "1h =2733.8kJ /kg蒸汽质量 m=V/"1v =1.1752kg查饱和蒸汽表得：2p =2bar 时，'2v =0.0010608kg m /3 "2v =0.88592kg m /3 '2h =504.7kJ /kg ''2h =2706.9kJ /kg 在冷却过程中，工质的容积、质量不变，故冷却前干饱和蒸汽的比容等于冷却后湿蒸汽的比容即： "1v =2x v或"1v =''22'22)1(v x v x +- 由于"1v ≈''22v x =≈"2"12v v x 0.5763 取蒸汽为闭系，由闭系能量方程 w u q +?=由于是定容放热过程，故0=w所以 1212u u u q -=?=而u =h -pv 故其中：2x h =''22'22)1(h x h x +-=1773.8kJ /kg 则 3.878-=q kJ /kgQ=mq=1.1752?(-878.3) =-1032.2kJ例2：1p =50bar C t 01400=的蒸汽进入汽轮机绝热膨胀至2p =0.04bar 。

习题提示与答案第六章 热能的可用性及火用分析6-1 汽车用蓄电池中储存的电能为1 440W ·h 。

现采用压缩空气来代替它。

设空气压力为6.5 MPa 、温度为25 ℃，而环境的压力为0.1MPa ，温度为25 ℃，试求当压缩空气通过容积变化而作出有用功时，为输出1 440 W ·h 的最大有用功所需压缩空气的体积。

提示：蓄电池存储的电能均为可转换有用功的火用 ，用压缩空气可逆定温膨胀到与环境平衡时所作出的有用功替代蓄电池存储的电能，其有用功完全来源于压缩空气的火用 ，即W u =me x ,U 1。

单位质量压缩空气火用 值()()()010010011,x s s T v v p u u e U ---+-=，空气作为理想气体处理。

答案：V =0.25 m 3。

6-2 有一个刚性容器，其中压缩空气的压力为3.0 MPa ，温度和环境温度相同为25 ℃，环境压力为0.1 MPa 。

打开放气阀放出一部分空气使容器内压力降低到1.0 MPa 。

假设容器内剩余气体在放气时按可逆绝热过程变化，试求：(1) 放气前、后容器内空气比火用U e x,的值；(2) 空气由环境吸热而恢复到25 ℃时空气的比火用U e x,的值。

提示：放气过程中刚性容器中剩余气体经历了一个等熵过程，吸热过程为定容过程；空气可以作为理想气体处理；各状态下容器中空气的比 火用()()()00000x s s T v v p u u e U ,---+-=。

答案：e x ,U 1=208.3 kJ/kg ，e x ,U 2=154.14 kJ/kg ，e x ,U 3=144.56kJ/kg 。

6-3 有0.1 kg 温度为17 ℃、压力为0.1 MPa 的空气进入压气机中，经绝热压缩后其温度为207 ℃、压力为0.4 MPa 。

若室温为17 ℃，大气压力为0.1 MPa ，试求该压气机的轴功，进、出口处空气的比 火用 H e x,。

工程热力学基本概念思 考 题1、如果容器中气体压力保持不变，那么压力表的读数一定也保持不变，对吗？答：不对。

因为压力表的读书取决于容器中气体的压力和压力表所处环境的大气压力两个因素。

因此即使容器中的气体压力保持不变，当大气压力变化时，压力表的读数也会随之变化，而不能保持不变。

2、“平衡”和“均匀”有什么区别和联系答：平衡（状态）值的是热力系在没有外界作用（意即热力、系与外界没有能、质交换，但不排除有恒定的外场如重力场作用）的情况下，宏观性质不随时间变化，即热力系在没有外界作用时的时间特征-与时间无关。

所以两者是不同的。

如对气-液两相平衡的状态，尽管气-液两相的温度，压力都相同，但两者的密度差别很大，是非均匀系。

反之，均匀系也不一定处于平衡态。

但是在某些特殊情况下，“平衡”与“均匀”又可能是统一的。

如对于处于平衡状态下的单相流体（气体或者液体）如果忽略重力的影响，又没有其他外场（电、磁场等）作用，那么内部各处的各种性质都是均匀一致的。

3、“平衡”和“过程”是矛盾的还是统一的？答：“平衡”意味着宏观静止，无变化，而“过程”意味着变化运动，意味着平衡被破坏，所以二者是有矛盾的。

对一个热力系来说，或是平衡，静止不动，或是运动，变化，二者必居其一。

但是二者也有结合点，内部平衡过程恰恰将这两个矛盾的东西有条件地统一在一起了。

这个条件就是：在内部平衡过程中，当外界对热力系的作用缓慢得足以使热力系内部能量及时恢复不断被破坏的平衡。

4、“过程量”和“状态量”有什么不同？答：状态量是热力状态的单值函数，其数学特性是点函数，状态量的微分可以改成全微分，这个全微分的循环积分恒为零；而过程量不是热力状态的单值函数，即使在初、终态完全相同的情况下，过程量的大小与其中间经历的具体路径有关，过程量的微分不能写成全微分。

因此它的循环积分不是零而是一个确定的数值。

习 题1-1 一立方形刚性容器，每边长 1 m ，将其中气体的压力抽至 1000 Pa ，问其真空度为多少毫米汞柱?容器每面受力多少牛顿？已知大气压力为 0.1MPa 。

第四章 理想气体的热力过程1．答：主要解决的问题及方法：1．根据过程特点（及状态方程）过程方程 2．根据过程方程始、终状态参数之间的关系 3．由热力学第一定律等 4．分析能量转换关系（用P —V 图及T —S 图）（根据需要可以定性也可以定量）例：1） 程方程式： （特征） （方程）2) 始、终状态参数之间的关系：3) 计算各量：4) 上工质状态参数的变化规律及能量转换情况闭口系：1—2过程−−→−确定−−→−确定−−→−计算s h u q t ∆∆∆,,,,,ωω常数=T 常数=PV 22111221V P V P V V P P ==或1212ln ln0P PR V V R s h u -==∆=∆=∆12121212lnlnln ln V V RT q V V RT V V RT V V PV V dVPV PdV t t =========⎰⎰ωωωωω图图，S T V P --000>>=∆q u ωω=⇒q开口系：1—2过程2．答：不是都适用。

第一组公式适用于任何一种过程。

第二组公式适用于定容过程，适用于定压过程。

3．答：定温过程对气体应加入热量。

4．答：对于一个定温过程，过程途径就已经确定了。

所以说是与途径有关的。

5．答：成立6．答：不只限于理想气体和可逆的绝热过程。

因为和是通用公式，适用于任何工质任何过程，只要是绝热过程无论是可逆还是不可逆。

所以和不只限于可逆绝热过程。

7． （1）（×）000>>=∆t q h ωt q ω=⇒)(12t t c u q v -=∆=)(12t t c h q p -=∆=12121212lnlnln ln V V RT q V V RT V V RT V V PV V dVPV PdV t t =========⎰⎰ωωωωωq w u q +∆=t w h q +∆=0=q 21u u w -=21h h w t -=（2）（×） （3）（×）8．答：q 1-2-3=Δu 1-2-3+w 1-2-3 ,q 1-4-3=Δu 1-4-3+w 1-4-3∵Δu 1-2-3=Δu 1-4-3, w 1-2-3 >w 1-4-3∴q 1-2-3> q 1-4-3b 、c 在同一条绝热线上，若b 、c 在同一条定温线上，二者相等。

第六章 水蒸气性质和蒸汽动力循环思 考 题1. 理想气体的热力学能只是温度的函数，而实际气体的热力学能则和温度及压力都有关。

试根据水蒸气图表中的数据，举例计算过热水蒸气的热力学能以验证上述结论。

[答]： 以500℃的过热水蒸汽为例，当压力分别为1bar 、30bar 、100bar 及300bar 时，从表中可查得它们的焓值及比容，然后可根据u h pv =-计算它们的热力学能，计算结果列于表中：由表中所列热力学能值可见：虽然温度相同，但由于是实际气体比容不同，热力学能值也不同。

2. 根据式(3-31)ch T pp =⎛⎝ ⎫⎭⎪⎡⎣⎢⎢⎤⎦⎥⎥∂∂可知：在定压过程中d h =c p d T 。

这对任何物质都适用，只要过程是定压的。

如果将此式应用于水的定压汽化过程，则得d h = c p d T =0（因为水定压汽化时温度不变，d T =0）。

然而众所周知 , 水在汽化时焓是增加的 (d h >0)。

问题到底出在哪里?[答] ：的确，d h =c p d T 可用于任何物质，只要过程是定压过程。

水在汽化时，压力不变，温度也不变，但仍然吸收热量（汽化潜热）吸热而不改变温度，其比热应为无穷大，即此处的p C 亦即为T C ，而T C =∞。

此时0dh =∞＝不定值，因此这时的焓差或热量（潜热）不同通过比热和温差的乘积来计算。

3. 物质的临界状态究竟是怎样一种状态？[答] ：在较低压力下，饱和液体和饱和蒸汽虽具有相同的温度和压力，但它们的密度却有很大的差别，因此在重力场中有明显的界面（液面）将气液两相分开，随着压力升高，两饱和相的密度相互接近，而在逼近临界压力（相应地温度也逼近临界温度）时，两饱和相的密度差逐渐消失。

流体的这种汽液两相无法区分的状态就是临界状态。

由于在临界状态下，各微小局部的密度起伏较大，引起光线的散射形成所谓临界乳光。

4. 各种气体动力循环和蒸汽动力循环，经过理想化以后可按可逆循环进行计算，但所得理论热效率即使在温度范围相同的条件下也并不相等。

第三章 理想气体的性质1.怎样正确看待“理想气体”这个概念？在进行实际计算是如何决定是否可采用理想气体的一些公式？答：理想气体：分子为不占体积的弹性质点，除碰撞外分子间无作用力。

理想气体是实际气体在低压高温时的抽象，是一种实际并不存在的假想气体。

判断所使用气体是否为理想气体（1）依据气体所处的状态（如：气体的密度是否足够小）估计作为理想气体处理时可能引起的误差；（2）应考虑计算所要求的精度。

若为理想气体则可使用理想气体的公式。

2.气体的摩尔体积是否因气体的种类而异？是否因所处状态不同而异？任何气体在任意状态下摩尔体积是否都是 0.022414m 3 /mol?答：气体的摩尔体积在同温同压下的情况下不会因气体的种类而异；但因所处状态不同而变化。

只有在标准状态下摩尔体积为 0.022414m 3 /mol3.摩尔气体常数 R 值是否随气体的种类不同或状态不同而异？ 答：摩尔气体常数不因气体的种类及状态的不同而变化。

4.如果某种工质的状态方程式为pv =R g T ，那么这种工质的比热容、热力学能、焓都仅仅是温度的函数吗？答：一种气体满足理想气体状态方程则为理想气体，那么其比热容、热力学能、焓都仅仅是温度的函数。

5.对于一种确定的理想气体，()p v C C -是否等于定值？p v C C 是否为定值？在不同温度下()p v C C -、pv C C 是否总是同一定值？答：对于确定的理想气体在同一温度下()p v C C -为定值，p v C C 为定值。

在不同温度下()p v C C -为定值，pv C C 不是定值。

6.麦耶公式p v g C C R -=是否适用于理想气体混合物？是否适用于实际气体？答：迈耶公式的推导用到理想气体方程，因此适用于理想气体混合物不适合实际气体。

7.气体有两个独立的参数，u(或 h)可以表示为 p 和 v 的函数，即(,)u u f p v =。

但又曾得出结论，理想气体的热力学能、焓、熵只取决于温度，这两点是否矛盾？为什么？答：不矛盾。

工程热力学思考题及答案第一章基本概念1.闭口系与外界无物质交换,系统内质量保持恒定，那么系统内质量保持恒定的热力系一定是闭口系统吗？答:不一定.稳定流动开口系统内质量也可以保持恒定。

2.有人认为，开口系统中系统与外界有物质交换，而物质又与能量不可分割，所以开口系统不可能是绝热系。

对不对,为什么?答：这种说法是不对的.工质在越过边界时，其热力学能也越过了边界。

但热力学能不是热量,只要系统和外界没有热量的交换就是绝热系。

3.平衡状态与稳定状态有何区别和联系，平衡状态与均匀状态有何区别和联系？答：只有在没有外界影响的条件下，工质的状态不随时间变化，这种状态称之为平衡状态。

稳定状态只要其工质的状态不随时间变化,就称之为稳定状态,不考虑是否在外界的影响下,这是它们的本质区别。

平衡状态并非稳定状态之必要条件。

物系内部各处的性质均匀一致的状态为均匀状态。

平衡状态不一定为均匀状态，均匀并非系统处于平衡状态之必要条件。

4.假如容器中气体的压力没有改变，试问安装在该容器上的压力表的读数会改变吗?绝对压力计算公式p = p b+p e(p >p b），p v=p b−p (p b〈p）中,当地大气压是否必定是环境大气压？答：压力表的读数可能会改变，根据压力仪表所处的环境压力的改变而改变。

当地大气压不一定是环境大气压。

环境大气压是指压力仪表所处的环境的压力.5.温度计测温的基本原理是什么？答：温度计随物体的冷热程度不同有显著的变化。

6.经验温标的缺点是什么？为什么?答:任何一种经验温标不能作为度量温度的标准。

由于经验温标依赖于测温物质的性质，当选用不同测温物质的温度计、采用不同的物理量作为温度的标志来测量温度时，除选定为基准点的温度，其他温度的测定值可能有微小的差异。

7.促使系统状态变化的原因是什么？答：系统内部各部分之间的传热和位移或系统与外界之间的热量的交换与功的交换都是促使系统状态变化。

8.(1)将容器分成两部分,一部分装气体，一部分抽成真空，中间是隔板。

《工程热力学》课程试卷一、是非（共12道题，每题1分，共12分）（对者√，错者×）1．公式d u = c v d t适用理想气体的任何过程。

（）2．孤立系统的熵与能量都是守恒的。

（）3．焓h = u + p v，对闭口系统，没有流动功，所以系统不存在焓这个参数。

（）4．当压力超过临界压力，温度低于临界温度，则H2O处在液态。

（）5．实际气体在压力趋于零的极限状态就成为理想气体。

（）6．容器中气体的压力不变则压力表的读数也绝对不会改变。

（）7．在T—S图上，任意二条可逆绝热过程线不能相交。

（）8．再热循环的主要目的是提高汽轮机尾部排汽干度。

（）9．热能利用系数完全地说明了热电循环的经济性能。

（）10．阴雨天中由于空气中增加了水蒸汽量，所以大气压力增大了。

（）11．膨胀功与流动功都是过程的函数。

（）12．水蒸汽在绝热节流前后，其温度可以发生变化。

（）二、选择（共13题，每题1分，共13分）13．压力为10 bar的气体通过渐缩喷管流入1 bar的环境中，现将喷管尾部截去一段，其流速、流量变化为（）。

（A）流速减小，流量不变（B）流速不变，流量增加（C）流速不变，流量不变（D）流速减小，流量增大14．P V = R T描述了（）的变化规律。

（A）任何气体准静态过程中（B）理想气体任意过程中（C）理想气体热力平衡状态（D）任何气体热力平衡状态15．某制冷机在热源T1= 300 K，及冷源T2= 250K之间工作，其制冷量为1000 KJ，消耗功为250 KJ，此制冷机是（）。

（C）（A）可逆的（B）不可逆的（C）不可能的（D）可逆或不可逆的16．系统的总储存能为（）。

（A）U （B）U + p V（C）（C）U + 122m c+m g z （D）U + p V + 122m c+m g z17．卡诺定理表明：所有工作于同温热源与同温泠源之间的一切热机的热效率为（）。

（A）（A）都相等，可以采用任何循环（B）（B）不相等，以可逆热机的热效率为最高（C）（C）都相等，仅仅取决与热源和泠源的温度（D）（D）不相等，与所采用的工质有关系18．通过叶轮轴对绝热刚性容器中的气体搅拌，其参数变化为（）。