Logistic回归分析报告结果解读分析.docx
- 格式:docx
- 大小:217.44 KB
- 文档页数:4

r语言logistic回归结果解读
在R语言中使用Logistic回归得到的结果可以帮助分析和解读数据中的因变量与自变量之间的关系。
以下是解读Logistic回归结果的一般步骤:
1. 检查模型的整体拟合优度:查看模型的拟合优度统计量,如AIC、BIC、Pseudo R-squared等。
较小的AIC和BIC值以及较大的Pseudo R-squared值指示着较好的模型拟合。
2. 检查自变量的显著性:通过解读每个自变量的系数估计值和相应的p-值来检查自变量是否对因变量有影响。
系数估计值表明自变量对因变量的影响方向和大小,而p-值则表示该影响是否显著。
通常,p-值小于0.05被认为是显著的。
3. 解释系数估计值:解释系数估计值可以帮助理解自变量的影响方向和大小。
正系数说明自变量增加时因变量的概率增加,负系数说明自变量增加时因变量的概率减少。
系数的绝对值越大,说明自变量的影响越大。
4. 计算和解释odds比:可以使用exp()函数将系数估计值转化为odds比,以更直观地解释自变量对因变量的影响。
例如,exp(系数估计值)表示odds比的增加或减少的倍数。
5. 预测和评估:使用模型进行预测和评估其准确性。
可以使用ROC曲线、AUC值、混淆矩阵等指标来评估模型的性能。
需要注意的是,解读Logistic回归结果需要结合具体问题和数
据的背景进行综合分析,确保结果的合理性和可靠性。
此外,还可以进行模型的诊断和改进,以提高模型的拟合和预测能力。

逻辑回归系数结果解读【原创版】目录1.引言:逻辑回归模型概述2.逻辑回归系数的含义3.逻辑回归系数的解读方法4.逻辑回归系数的应用实例5.总结正文1.引言:逻辑回归模型概述逻辑回归(Logistic Regression)是一种广泛应用于分类领域的统计学习方法。
它的原理是利用 sigmoid 函数将线性模型的输出映射到 0 到 1 之间,表示为某一类的概率。
逻辑回归模型的核心是系数,它们决定了特征与目标变量之间的关联程度。
本文将介绍如何解读逻辑回归系数的结果。
2.逻辑回归系数的含义在逻辑回归模型中,每个自变量对应一个系数。
系数表示当其他变量保持不变时,该自变量每变动一个单位,目标变量的对数几率发生的变化。
具体来说,如果一个特征的系数为正,那么该特征与目标变量正相关;如果系数为负,那么该特征与目标变量负相关。
3.逻辑回归系数的解读方法逻辑回归系数的绝对值大小可以衡量特征与目标变量的关联强度。
绝对值越大,表示特征与目标变量的关联程度越高。
此外,我们还可以通过比较不同特征的系数大小,确定各个特征对目标变量的相对重要性。
4.逻辑回归系数的应用实例假设我们有一个逻辑回归模型,用于预测某人是否患有心脏病。
模型中有以下三个特征:年龄、胆固醇水平和血压。
对应的系数分别为:年龄系数为 0.1,胆固醇水平系数为 0.2,血压系数为 0.3。
根据系数,我们可以得出以下结论:- 年龄对心脏病发病率的影响相对较小。
- 胆固醇水平对心脏病发病率的影响较大。
- 血压对心脏病发病率的影响最大。
根据这些结论,我们可以为医生提供有针对性的建议,帮助他们更好地诊断病情。
5.总结逻辑回归模型的系数对于理解特征与目标变量之间的关系具有重要意义。

stata二元logistic回归结果解读在Stata中进行二元Logistic回归分析后,你将得到一系列的输出结果。
以下是如何解读这些结果的简要指南:1.模型拟合信息:●Pseudo R-squared :伪R方值,表示模型对数据的拟台程度。
其值介于0和1之间,越接近1表示模型拟合越好。
●Lkliloo ratio test :似然比检验,用于检验模型的整体拟台优度。
2.系数估计值:●B:回归系数,表示自变显每变化-一个单位时,因变显的预测值的变化。
●odds Ratio :优势比。
表示自变量变化-个单位时。
事件发生与不发生的比率的倍数。
计算公式为exp(B) 。
3.显菩性检验:●Pr(>2D:P值,用于检验回归系数的显著性。
通常,如果P值小于预设的显著性水平(如0.05) ,则认为该变量在统计上是显著的。
4. 95%置信区间:●Lower 和Upper:分别为回归系数的95%置信区间的下限和上限。
如果这个区间不包含0,那么我们可以认为该变量对事件的发生有影响。
5.变量信息:●x:自变量名称。
●e(b): Stata自动计算并给出的回归系数估计值。
●(exp(b) :优势比的计算值。
● 伊用:参考类别。
对于分类变量,Stata默认使用第一个类别作为参考类别。
6.模型假设检验:●Heteroskedasticiy:异方差性检验,用于检验误差项的方差是否恒定。
如果存在异方差性,可能需要考虑其他的回归模型或者对模型进行修正。
●Linearity:线性关系检验,用于检验自变量和因变量之间是否为线性关系。
如果不是线性关系,可能需要考虑其他形式的模型或者使用其他转换方法。
7.模型诊断信息:● AlIC, BIC:用于评估模型复杂度和拟合优度的统计星。
较低的值表示更好的拟合。
●Hosmer-Lemeshow test: 霍斯默勒梅肖检验,用于检验模型是否符合Logistic回归的前提假设(比如比例优势假设)。
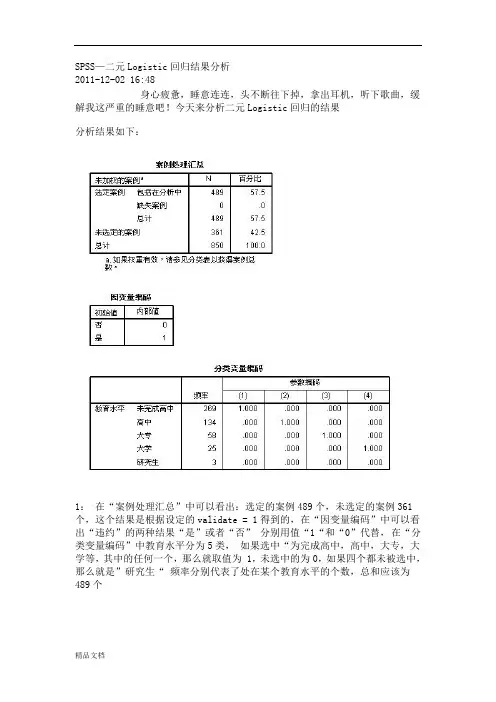
SPSS—二元Logistic回归结果分析2011-12-02 16:48身心疲惫,睡意连连,头不断往下掉,拿出耳机,听下歌曲,缓解我这严重的睡意吧!今天来分析二元Logistic回归的结果分析结果如下:1:在“案例处理汇总”中可以看出:选定的案例489个,未选定的案例361个,这个结果是根据设定的validate = 1得到的,在“因变量编码”中可以看出“违约”的两种结果“是”或者“否” 分别用值“1“和“0”代替,在“分类变量编码”中教育水平分为5类,如果选中“为完成高中,高中,大专,大学等,其中的任何一个,那么就取值为 1,未选中的为0,如果四个都未被选中,那么就是”研究生“ 频率分别代表了处在某个教育水平的个数,总和应该为489个1:在“分类表”中可以看出:预测有360个是“否”(未违约)有129个是“是”(违约)2:在“方程中的变量”表中可以看出:最初是对“常数项”记性赋值,B为-1.026,标准误差为:0.103那么wald =( B/S.E)²=(-1.026/0.103)² = 99.2248, 跟表中的“100.029几乎接近,是因为我对数据进行的向下舍入的关系,所以数据会稍微偏小,B和Exp(B) 是对数关系,将B进行对数抓换后,可以得到:Exp(B) = e^-1.026 = 0.358, 其中自由度为1, sig为0.000,非常显著1:从“不在方程中的变量”可以看出,最初模型,只有“常数项”被纳入了模型,其它变量都不在最初模型内表中分别给出了,得分,df , Sig三个值, 而其中得分(Score)计算公式如下:(公式中(Xi- X¯) 少了一个平方)下面来举例说明这个计算过程:(“年龄”自变量的得分为例)从“分类表”中可以看出:有129人违约,违约记为“1”则违约总和为 129,选定案例总和为489那么: y¯ = 129/489 = 0.2638036809816x¯ = 16951 / 489 = 34.664621676892所以:∑(Xi-x¯)² = 30074.9979y¯(1-y¯)=0.2638036809816 *(1-0.2638036809816 )=0.19421129888216则:y¯(1-y¯)* ∑(Xi-x¯)² =0.19421129888216 * 30074.9979 = 5 840.9044060372则:[∑Xi(yi - y¯)]^2 = 43570.8所以:=43570.8 / 5 840.9044060372 = 7.4595982010876 = 7.46 (四舍五入)计算过程采用的是在 EXCEL 里面计算出来的,截图如下所示:从“不在方程的变量中”可以看出,年龄的“得分”为7.46,刚好跟计算结果吻合!!答案得到验证~!!!!1:从“块1” 中可以看出:采用的是:向前步进的方法,在“模型系数的综合检验”表中可以看出:所有的SIG 几乎都为“0”而且随着模型的逐渐步进,卡方值越来越大,说明模型越来越显著,在第4步后,终止,根据设定的显著性值和自由度,可以算出卡方临界值,公式为:=CHIINV(显著性值,自由度) ,放入excel就可以得到结果2:在“模型汇总“中可以看出:Cox&SnellR方和 Nagelkerke R方拟合效果都不太理想,最终理想模型也才:0.305 和 0.446,最大似然平方的对数值都比较大,明显是显著的似然数对数计算公式为:计算过程太费时间了,我就不举例说明计算过程了Cox&SnellR方的计算值是根据:1:先拟合不包含待检验因素的Logistic模型,求对数似然函数值INL0 (指只包含“常数项”的检验)2:再拟合包含待检验因素的Logistic模型,求新的对数似然函数值InLB (包含自变量的检验)再根据公式:即可算出:Cox&SnellR 方的值!提示:将Hosmer 和 Lemeshow 检验和“随机性表” 结合一起来分析1:从Hosmer 和 Lemeshow 检验表中,可以看出:经过4次迭代后,最终的卡方统计量为:11.919,而临界值为:CHINV(0.05,8) = 15.507卡方统计量< 临界值,从SIG 角度来看: 0.155 > 0.05 , 说明模型能够很好的拟合整体,不存在显著的差异。

多分类无序logistic回归的结果解读涉及多个步骤。
首先,你需要对模型的整体情况进行描述,例如R方值。
然后,逐一分析X对于Y(相对于的对比项)的影响情况。
如果X对应的P值小于0.05,则说明X 会对Y(相对于的对比项)产生影响关系,此时可结合OR值进一步分析影响幅度。
以一个具体的例子来说明:你正在研究影响总统候选人民主党支持度的因素,包括年龄、学历和性别。
你使用多分类无序logistic回归进行数据分析。
1. 模型整体情况:首先,你描述了模型的R方值。
例如,模型伪R 平方值(McFadden R平方)为0.025,意味着年龄、学历、性别可以解释总统候选人民主党支持率的
2.45%变化原因。
2. 影响因素分析:接下来,你逐一分析了年龄、学历和性别对民主党支持率的影响。
年龄:P值大于0.05,说明年龄对民主党支持率没有显著影响。
学历:P值小于0.05,说明学历对民主党支持率有显著影响。
进一步分析OR值,如果OR值大于1,说明高学历更有可能支持民主党;如果OR值小于1,则说明低学历更有可能支持民主党。
性别:P值小于0.05,说明性别对民主党支持率有显著影响。
进一步分析OR值,如果OR值大于1,说明女性更有可能支持民主党;如果OR值小于1,则说明男性更有可能支持民主党。
3. 总结:基于以上分析,你得出结论:学历和性别对总统候选人民主党支持率有显著影响,而年龄没有明显影响。
同时,你也给出了具
体的影响幅度。
以上是一个基本的多分类无序logistic回归结果解读示例。
具体解读可能因数据和研究目的而有所不同。

Logistic回归是一种统计方法,用于研究分类变量与一系列解释变量之间的关系。
单因素和多因素logistic回归是该方法的两种常见类型。
在单因素logistic回归中,研究者一次只考虑一个解释变量对因变量的影响。
这种方法主要用于初步探索哪些变量可能对因变量有影响,但结果可能受到混杂因素的影响,因此可能不是非常可靠。
在多因素logistic回归中,研究者考虑所有可能的影响因素。
这种方法能够校正各种混杂因素的影响,因此结果更加可信。
多因素分析通常在单因素分析的基础上进行,以全面了解各因素对因变量的综合影响。
解读结果时,应注意模型的拟合度、变量的显著性等指标。
对于单因素分析,应关注该变量对因变量的影响是否显著。
对于多因素分析,应关注该变量在控制其他因素后对因变量的影响,以及该变量与其他变量的交互作用。
总之,单因素和多因素logistic回归是研究分类变量与解释变量之间关系的常用方法。
在解读结果时,应注意模型的拟合度和变量的显著性等指标,以全面了解各因素对因变量的影响。



Logistic回归分析报告结果解读分析Logistic回归常用于分析二分类因变量(如存活和死亡、患病和未患病等)与多个自变量的关系。
比较常用的情形是分析危险因素与是否发生某疾病相关联。
例如,若探讨胃癌的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群有不同的临床表现和生活方式等,因变量就为有或无胃癌,即“是"或“否”,为二分类变量,自变量包括年龄、性别、饮食习惯、是否幽门螺杆菌感染等。
自变量既可以是连续变量,也可以为分类变量.通过Logistic 回归分析,就可以大致了解胃癌的危险因素。
Logistic回归与多元线性回归有很多相同之处,但最大的区别就在于他们的因变量不同.多元线性回归的因变量为连续变量;Logistic回归的因变量为二分类变量或多分类变量,但二分类变量更常用,也更加容易解释.1.Logistic回归的用法一般而言,Logistic回归有两大用途,首先是寻找危险因素,如上文的例子,找出与胃癌相关的危险因素;其次是用于预测,我们可以根据建立的Logistic回归模型,预测在不同的自变量情况下,发生某病或某种情况的概率(包括风险评分的建立)。
2.用Logistic回归估计危险度所谓相对危险度(risk ratio,RR)是用来描述某一因素不同状态发生疾病(或其它结局)危险程度的比值。
Logistic回归给出的OR(odds ratio)值与相对危险度类似,常用来表示相对于某一人群,另一人群发生终点事件的风险超出或减少的程度。
如不同性别的胃癌发生危险不同,通过Logistic回归可以求出危险度的具体数值,例如1。
7,这样就表示,男性发生胃癌的风险是女性的1.7倍。
这里要注意估计的方向问题,以女性作为参照,男性患胃癌的OR是1。
7。
如果以男性作为参照,算出的OR将会是0。
588(1/1。
7),表示女性发生胃癌的风险是男性的0.588倍,或者说,是男性的58.8%。

stata多元logistic回归结果解读【原创版】目录一、什么是多元 logistic 回归二、多元 logistic 回归的结果解读1.Odds ratio(风险比)2.显著性水平(sig.)3.系数估计4.模型整体检验三、实例分析四、总结正文一、什么是多元 logistic 回归多元 logistic 回归是一种用于分析多自变量与二分类因变量之间关系的统计模型。
它可以帮助我们了解各个自变量对因变量的影响程度以及预测概率。
在 Stata 中,我们可以使用 logistic 回归命令进行分析,例如:logit depvar indepvar1 indepvar2...,其中 depvar 表示因变量,indepvar1、indepvar2 等表示自变量。
二、多元 logistic 回归的结果解读1.Odds ratio(风险比)Odds ratio(风险比)是一种衡量自变量对因变量影响程度的指标。
它表示当某个自变量取某一值时,事件发生的概率与该自变量取另一值时事件发生概率的比值。
在 Stata 结果中,我们可以看到每个自变量的 OR 值,正值表示该自变量与因变量正相关,负值表示负相关,接近 1 表示关系较弱。
2.显著性水平(sig.)显著性水平是用来判断自变量对因变量影响是否显著的指标。
在Stata 结果中,我们可以看到每个自变量的 sig.值。
一般而言,sig.值小于 0.05,我们认为该自变量对因变量的影响是显著的;sig.值大于等于 0.05,我们认为该自变量对因变量的影响不显著。
3.系数估计系数估计表示自变量对因变量的影响程度。
在 Stata 结果中,我们可以看到每个自变量的系数估计值。
系数值越大,表示该自变量对因变量的影响越大;系数值越小,表示影响越小。
4.模型整体检验模型整体检验可以帮助我们判断模型是否整体上显著。
在 Stata 中,我们可以使用 logistic 命令进行模型整体检验,例如:logit depvar indepvar1 indepvar2..., test(1)。

logistic回归结果解读Logistic回归是一种分类方法,主要应用于预测响应变量是二进制的情况,比如成功与失败、健康与疾病、风险与无风险等。
它相当于在特征区间内,将所有样本划分为两类,从而实现对数据集中每个样本的分类,并有效地实现了二元分类。
在衡量模型效果方面,logistic回归采用了准确率、召回率和ROC曲线等评估指标,可以更好地检验模型的性能。
Logistic回归结果解读是指解读Logistic回归模型的输出结果,其中包括:模型的性能、特征的重要性、概率和拟合度等。
首先,模型的性能是模型解释的重点。
Logistic回归模型一般使用AUC(Area Under Curve)值来衡量模型的性能,AUC值越大,模型的性能越好。
此外,查准率(Precision)和查全率(Recall)也是用来评估Logistic 回归模型性能的重要指标,查准率表示样本中被正确预测的个体占预测个体总数的比率,而查全率表示样本中被预测正确的个体占实际个体总数的比率。
其次,Logistic回归模型的参数可以用来判断特征变量对模型的重要性,通常来说,Wald检验的p值越小,特征变量对模型的重要性越大,反之,特征变量对模型的重要性越小。
最后,Logistic回归模型可以给出每个样本的概率,这样可以更加直观地看出模型的拟合度。
如果模型拟合度较差,说明存在模型拟合不足,此时可以对模型进行调整,比如添加新的特征变量或者更改模型的参数,以提高拟合度。
总的来说,Logistic回归结果的解读是一个重要的环节,它可以帮助我们更好地理解模型的性能、特征的重要性以及概率和拟合度。
只有解读了模型的结果,才能更好地分析模型的效果,并对模型进行调整,以达到更好的性能。
在二元Logistic回归分析中,结果解读主要涉及到模型的拟合优度以及各个自变量的影响程度。
首先,模型的拟合优度可以通过一些统计检验来进行评估,例如Hosmer-Lemeshow检验。
如果检验结果的P值大于0.05(例如,sig=0.533>0.05),则可以认为模型的拟合优度较高,模型能够较好地拟合实际数据。
其次,对于自变量(也称为解释变量或预测因子)的解读,主要关注其回归系数(B值)、标准误、P值、以及Odds Ratio(OR值)。
以肿瘤家族史为例,如果有统计学意义(即P<0.05),则表明肿瘤家族史对于二元Logistic回归模型的因变量(也称为响应变量或结果变量)有显著影响。
回归系数(B值)表示了自变量每增加一个单位,因变量发生比的对数变化量。
标准误用于衡量回归系数的稳定性和可靠性。
P值用于判断自变量是否对因变量有显著影响。
通常,如果P<0.05,则认为自变量对因变量的影响是显著的。
Odds Ratio(OR值)是二元Logistic回归分析中一个非常重要的指标,它表示了自变量每增加一个单位,因变量发生的概率与不发生的概率的比值(即发生比)的变化情况。
以肿瘤家族史为例,OR=7.563意味着有肿瘤家族史的人患鼻咽癌的概率是无肿瘤家族史的7.563倍。
需要注意的是,对于分类变量的解读要特别注意其参照类别。
在二元Logistic回归分析中,通常会将某一类别作为参照类别,其他类别与之进行比较。
因此,在解读结果时,要明确各个类别与参照类别的比较情况。
非条件logistic 回归结果解读
非条件logistic回归是一种用于预测二分类问题的回归分析方法。
对于非条件logistic回归的结果进行解读,可以从以下几
个方面进行分析:
1. 回归系数:非条件logistic回归模型的回归系数表示自变量
对因变量的影响程度。
如果回归系数为正,表示该自变量与因变量呈正相关关系,即自变量增加时,因变量的概率也会增加;如果回归系数为负,表示该自变量与因变量呈负相关关系。
回归系数的大小可以用来判断自变量对因变量的重要程度,绝对值越大表示影响越大。
2. 模型拟合度:非条件logistic回归模型的拟合度可以通过R
方(R-squared)或者对数似然比(log-likelihood)来评估。
R
方的取值范围为0到1,越接近1表示模型的拟合度越好;而
对数似然比越大表示模型的拟合度越好。
需要注意的是,拟合度高并不一定意味着模型预测准确度高,还需要考虑其他评估指标。
3. p值:非条件logistic回归模型的p值可以用来判断自变量
的显著性。
p值越小,表示该自变量对因变量的影响越显著。
通常,p值小于0.05被认为是显著的。
如果p值超过设定的显
著性水平,就需要谨慎解释该自变量对因变量的影响。
4. 假设检验:非条件logistic回归模型通常会进行一些假设检验,如对模型的合理性、模型参数的正态分布等。
如果假设检验不通过,就需要重新考虑模型的建立和解释。
需要注意的是,非条件logistic回归模型的结果解读还需要考虑实际问题和数据的背景。
同时,还需要结合其他统计学方法和领域知识来对结果进行综合分析和解释。
Logistic回归模型一、Logistic分布的概率密度函数及图形:f(x)=exp(-x)/(1+exp(-x))^2;(选取的x值是-14至14)二、Logistic分布的分布函数及图形:F(x)=exp(x)/(1+exp(x));(选取的x值是-14至14)三、在clementine中建立logistic回归模型及输出结果分析:选取80%的数据,在clementine中,以工作状况,家庭住址,教育程度,所在地区,退休与否,婚姻状况,性别,年龄和收入9个变量为自变量,以电信客户流失状况为因变量,建立logistic模型。
以下为输出的结果分析。
1、变量重要性分析:如下图所示,9个变量对客户流失的影响作用不一样,其中工作状况是影响最大的变量,其比重为0.376。
另外,教育程度(比重为0.225)和家庭地址(比重为0.223)的影响也比较明显。
而年龄几乎不是影响因素。
2、单个变量显著性及系数经济意义分析:下图中,B为自变量的回归系数,若B为负则代表该自变量与因变量呈反向变动的关系。
S.E.是标准差;Wald指的是Wald统计量;df是指自由度;sig.指的是显著性(其值越小说明自变量对因变量的影响越显著);Exp(B)代表着各自变量的回归系数的经济意义,即在保持其他条件不变时,特定自变量变动1单位时,所影响到发生率的变化率为B单位。
从图中可以看出,工作状况对因变量的影响是完全显著,其系数为-0.064,说明了工作状况与客户流失之间的反向变动关系,且当其他自变量保持不变的条件下,消费者的工作状态每变动1单位,所带来的客户流失的发生率的变化率为0.064个单位。
这与实际情况相符合。
其次,教育程度,家庭住址和婚姻状况对因变量的影响也较显著,这可能与电信的宣传策略和信号覆盖以及状况相关。
然而,其他变量的显著性水平就比较低。
其中收入的显著性最差,可能是因为各个通信公司的服务价格与质量区别不大,收入水平对客户流失情况影响很小。
Logistic回归分析(logit回归)一般可分为3类,分别是二元logistic回归分析、多分类Logistic回归分析和有序Logistic回归分析。
logistic回归分析类型如下所示。
Logistic回归分析用于研究X对Y的影响,并且对X的数据类型没有要求,X可以为定类数据,也可以为定量数据,但要求Y必须为定类数据,并且根据Y的选项数,使用相应的数据分析方法。
如果Y有两个选项,如愿意和不愿意、是和否,那么应该使用有序logistic回归分析(SPSSAU进阶方法->二元logit);如果Y有多个选项,并且各个选项之间可以对比大小,例如,1代表“不愿意”,2代表“无所谓”,3代表“愿意”,这3个选项具有对比意义,数值越高,代表样本的愿意程度越高,那么应该使用多元有序Logistic回归分析(SPSSAU进阶方法->有序logit);如果Y有多个选项,并且各个选项之间不具有对比意义,例如,1代表“淘宝”,2代表“天猫”,3代表“京东”,4代表“亚马逊中国”,数值仅代表不同类别,数值大小不具有对比意义,那么应该使用多元无序Logistic回归分析(SPSSAU进阶方法->多分类logit)。
1、有序logistic回归分析基本说明进行有序logistic回归时,通常需要有以下步骤,分别是连接函数选择,平行性检验,模型似然比检验,参数估计分析,模型预测准确效果共5个步骤。
1) 连接函数选择SPSSAU共提供五类连接函数,分别如下:SPSSAU默认使用logit连接函数,如果模型没有特别的要求,应该首选使用logit连接函数,尤其是因变量的选项数量很少的时候。
连接函数可能会对平行性检验起到影响,如果平行性检验无法通过时,可考虑选择更准确的连接函数进行尝试。
正常情况下使用默认的logit连接函数即可。
2) 平行性检验一般来说,模型最好通过平行性检验,但在研究中很可能出现无法通过的现象。
Logistic回归分析报告结果解读分析Logistic回归常用于分析二分类因变量(如存活和死亡、患病和未患病等)与多个自变量的关系。
比较常用的情形是分析危险因素与是否发生某疾病相关联。
例如,若探讨胃癌的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群有不同的临床表现和生活方式等,因变量就为有或无胃癌,即“是”或“否”,为二分类变量,自变量包括年龄、性别、饮食习惯、是否幽门螺杆菌感染等。
自变量既可以是连续变量,也可以为分类变量。
通过Logistic回归分析,就可以大致了解胃癌的危险因素。
Logistic回归与多元线性回归有很多相同之处,但最大的区别就在于他们的因变量不同。
多元线性回归的因变量为连续变量;Logistic回归的因变量为二分类变量或多分类变量,但二分类变量更常用,也更加容易解释。
1.Logistic回归的用法
一般而言,Logistic回归有两大用途,首先是寻找危险因素,如上文的例子,找出与胃癌相关的危险因素;其次是用于预测,我们可以根据建立的Logistic回归模型,预测在不同的自变量情况下,发生某病或某种情况的概率(包括风险评分的建立)。
2.用Logistic回归估计危险度
所谓相对危险度(risk ratio,RR)是用来描述某一因素不同状态发生疾病(或其它结局)危险程度的
比值。
Logistic回归给出的OR(odds ratio)值与相对危险度类似,常用来表示相对于某一人群,另一人群发生终点事件的风险超出或减少的程度。
如不同性别的胃癌发生危险不同,通过Logistic回归可以求出危险度的具体数值,例如1.7,
这样就表示,男性发生胃癌的风险是女性的1.7倍。
这里要注意估计的方向问题,以女性作为参照,男性患胃癌的OR是1.7。
如果以男性作为参照,算出的OR将会是0.588(1/1.7),表示女性发生胃癌的风险是男性的0.588倍,或者说,是男性的58.8%。
撇开了参照组,相对危险度就没有意义了。
Logistic回归在医学研究中广泛使用的原因之一,就是模型直接给出具有临床实际意义的OR值,很大程度上方便了结果的解读与推广。
图1 相对危险度(risk ratio,RR)与OR(odds ratio)的表达
3. Logistic报告OR值或β值
在Logistic回归结果汇报时,往往会遇到这样一个问题:是应该报告OR值,
还是β值,还是两个都要报告?这个决定权最终当然还是作者本人,但有一点需要进一步了解:OR值和β值其实是等价的。
图2 OR值与β值的公式推导
4 Logistic回归结果判读
“EXP(B)”即为相应变量的OR值(又叫优势比,比值比),为在其他条件不变的情况下,自变量每改变1个单位,事件的发生比“Odds”的变化率。
伪决定系数cox & Snell R2和Nagelkerke R2,这两个指标从不同角度反映了当前模型中自变量解释了因变量的变异占因变量总变异的比例。
但对于Logistic回归而言,通常看到的伪决定系数的大小不像线性回归模型中的决定系数那么大。
预测结果列联表解释,看”分类表“中的数据,提供了2类样本的预测正确率和总的正确率。
建立Logistic回归方程
logit(P)=β0+β1*X1+β2*X2+……+βm*Xm
图2 Logistic回归结果报告样例。