下载文档原格式
五法求二面角从全国19份高考试卷中我们知道，立体几何题中命有求二面角大小的试题共有12份，并都为分值是12分的大题，足以说明这一知识点在高考中的位置，据有关专家分析，它仍然是2010年高考的重点，因此，我们每位考生必须注意，学会其解题方法，掌握其解题技巧，是十分重要的。
一、 定义法：从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面，在棱上取点，分别在两面内引两条射线与棱垂直，这两条垂线所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。
如例1中从二面角S —AM —B 中半平面ABM 上的一已知点（B ）向棱AM 作垂线，得垂足（F ）；在另一半平面ASM 内过该垂足（F ）作棱AM 的垂线（如GF ），这两条垂线（BF 、GF ）便形成该二面角的一个平面角，再在该平面角内建立一个可解三角形，然后借助直角三角函数、正弦定理与余弦定理解题。
例1（2009全国卷Ⅰ理）如图，四棱锥S ABCD -中，底面ABCD 为矩形，SD ⊥底面ABCD，AD =2DC SD ==，点M 在侧棱SC 上，ABM ∠=60°（I ）证明：M 在侧棱SC 的中点 （II ）求二面角S AM B --的大小。
证（I ）略解（II ）：利用二面角的定义。
在等边三角形ABM 中过点B作BF AM ⊥交AM 于点F ，则点F 为AM 的中点，过F 点在平面ASM 内作GF AM ⊥，GF 交AS 于G ，连结AC ，∵△ADC ≌△ADS ，∴AS-AC ，且M 是SC 的中点， ∴AM ⊥SC ， GF ⊥AM ，∴GF ∥AS ，又∵F 为AM 的中点，∴GF 是△AMS 的中位线，点G 是AS 的中点。
则GFB ∠即为所求二面角. ∵2=SM ，则22=GF ，又∵6==AC SA ，∴2=AM ∵2==AB AM ，060=∠ABM ∴△ABM 是等边三角形，∴3=BF在△GAB 中，26=AG ，2=AB ，090=∠GAB ，∴211423=+=BG FG366232222113212cos 222-=-=⨯⨯-+=⋅-+=∠FB GF BG FB GF BFG ∴二面角S AM B --的大小为)36arccos(-练习1（2008山东）如图，已知四棱锥P -ABCD ，底面ABCD 为菱形，P A ⊥平面ABCD ，60ABC ∠=︒,E ，F 分别是BC , PC 的中点. （Ⅰ）证明：AE ⊥PD ;（Ⅱ）若H 为PD 上的动点，EH 与平面P AD 所成最大角E —AF —C 的余弦值. 分析：第1题容易发现，可通过证AE ⊥AD 后推出AE ⊥平面APD ，使命题获证，而第2题，则首先必须在找到最大角正切值有关的线段计算出各线段的长度之后，考虑到运用在二面角的棱AF 上找到可计算二面角的平面角的顶点S ，和两边SE 与SC ，进而计算二面角的余弦值。
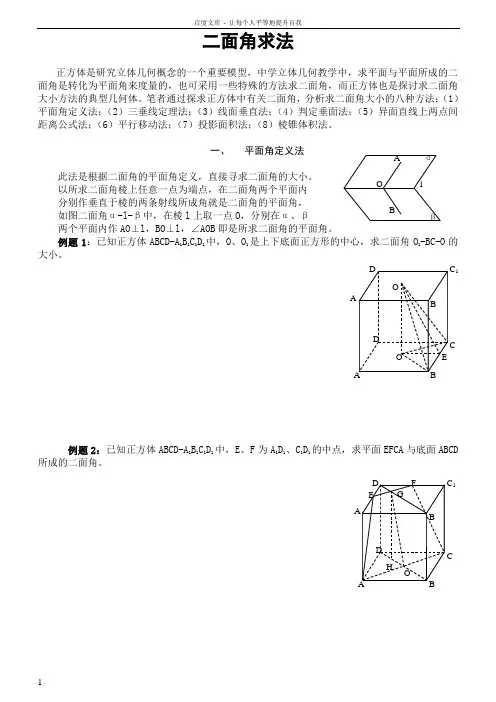
二面角求法正方体是研究立体几何概念的一个重要模型，中学立体几何教学中，求平面与平面所成的二面角是转化为平面角来度量的，也可采用一些特殊的方法求二面角，而正方体也是探讨求二面角大小方法的典型几何体。
笔者通过探求正方体中有关二面角，分析求二面角大小的八种方法：（1）平面角定义法；（2）三垂线定理法；（3）线面垂直法；（4）判定垂面法；（5）异面直线上两点间距离公式法；（6）平行移动法；（7）投影面积法；（8）棱锥体积法。
一、平面角定义法此法是根据二面角的平面角定义，直接寻求二面角的大小。
以所求二面角棱上任意一点为端点，在二面角两个平面内分别作垂直于棱的两条射线所成角就是二面角的平面角，如图二面角α-l-β中，在棱l上取一点O，分别在α、β两个平面内作AO⊥l，BO⊥l，∠AOB即是所求二面角的平面角。
例题1：已知正方体ABCD-A1B1C1D1中，O、O1是上下底面正方形的中心，求二面角O1-BC-O的大小。
例题2：已知正方体ABCD-A1B1C1D1中，E、F为A1D1、C1D1的中点，求平面EFCA与底面ABCD所成的二面角。
二、 利用三垂线定理法此方法是在二面角的一个平面内过一点作另一个面的垂线，再由垂足（或仍是该点）作棱的垂线，连接该点和棱上的垂足（或连两垂足）两点线，即可得二面角的平面角。
如图二面角α-l-β中，在平面α内取一点A ，过A 作AB ⊥平面β，B 是垂足， 由B （或A ）作BO （或AO ）⊥l ，连接AO （或BO ）即得AO 是平面β的斜线， BO 是AO 在平面β中的射影，根据三垂线定理（或逆定理）即得AO ⊥l ，BO ⊥l ， 即∠AOB 是α-l-β的平面角。
例题3：已知正方体ABCD-A 1B 1C 1D 1中，求二面角B-AC-B 1的大小。
例题4：已知正方体ABCD-A 1B 1C 1D 1中，求平面ACD 1与平面BDC 1所成的二面角。
三、 线面垂直法此法利用直线垂直平面即该直线垂直平面内任何直线的性质来寻求二面角的平面角。
二面角求法1 .定义法即在二面角的棱上找一点，在二面角的两个面内分别作棱的射线即得二面角的平面角.·例1 . 正方体ABCD-A 1B 1C 1D 1中，求 二面角A-BD-C 1解析：易知∠COC 1是二面角C-BD-C 1的平面角，且tan ∠COC 1例2.在锥体P-ABCD 中，ABCD 是边长为1的菱形，且∠DAB=60︒，PA PD ==分别是BC,PC 的中点.求：二面角P-AD-B 的余弦值.&解：由（1）知PGB ∠为二面角P AD B --的平面角，在Rt PGA ∆中，2217()24PG =-=；在Rt BGA ∆中，222131()24BG =-=；在PGB ∆中，222cos 2PG BG PB PGB PG BG +-∠==⋅.2 三垂线法此法最基本的一个模型为：如图3，设锐二面角βα--l ，过面α 内一点P 作PA ⊥α于A ，作AB ⊥l 于B ，连接PB ，由三垂线定理得PB ⊥l ，则∠PBA 为二面角βα--l 的平面角，故称此法为三垂线法.《例3.如图4，平面α⊥平面β，α∩β=l ，A ∈α，B ∈β，点A 在直线l 上的射影为A 1，点B 在l 的射影为B 1，已知AB=2，AA 1=1，BB 1=2， 求：二面角A 1－AB －B 1的正弦值.分析与略解：作A 1E ⊥AB 1于AB 1于E ，则可证A 1E ⊥平面AB 1B.@—A图3αβP￥BlB 1 A *A 1l%EF@PCＳ| FGP AＳBＳ;C DＳF E,过E 作EF ⊥AB 交AB 于F ，连接A 1F ，则得A 1F ⊥AB ， ∴∠A 1FE 就是所求二面角的平面角.依次可求得 AB 1=B 1B=2，A 1B=3，A 1E=22，A 1F=23， 则在Rt △A 1EF 中，sin ∠A 1FE=A 1E A 1F =63 .·例4.如图所示,在四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD,点E 在线段PC 上,PC ⊥平面BDE.若PA=1,AD=2,求二面角B-PC-A 的正切值.】解:由(1)得BD ⊥平面PAC, ∴BD ⊥AC.又四边形ABCD 为矩形,∴四边形ABCD 是正方形.设AC 交BD 于O 点,∵PC ⊥平面BDE,∴∠BEO 即为二面角B-PC-A 的平面角. ∵PA=1,AD=2,∴AC=2,BO=OC=,∴PC==3,—又OE===在直角三角形BEO 中,tan ∠BEO===3,∴二面角B-PC-A 的正切值为3.例5. 如图, 四棱锥P-ABCD 中, 底面ABCD 为矩形, PA ⊥底面ABCD, PA=AB=, 点E 是棱PB 的中点.(1) 若AD=, 求二面角A-EC-D的平面角的余弦值.—(1) 过点D作DF⊥CE, 交CE于F, 过点F作FG⊥CE, 交AC于G, 则∠DFG为所求的二面角的平面角.由(Ⅰ) 知BC⊥平面PAB, 又AD∥BC, 得AD⊥平面PAB, 故AD⊥AE, 从而DE==. 在Rt△CBE中, CE==. 由CD=, 所以△CDE为等边三角形, 故F为CE的中点, 且DF=CD·sin=.因为AE⊥平面PBC, 故AE⊥CE, 又FG⊥CE, 知FG=AE, 从而FG=, 且G点为AC的中点. 连结DG, 则在Rt△ADG中, DG=AC==.，所以cos∠DFG==.、3、向量法向量法解立体几何中是一种十分简捷的也是非常传统的解法，可以说所有的立体几何题都可以用向量法求解，用向量法解立体几何题时，通常要建立空间直角坐标系，写出各点的坐标，然后将几何图中的线段写成用坐标法表示的向量，进行向量计算解题。
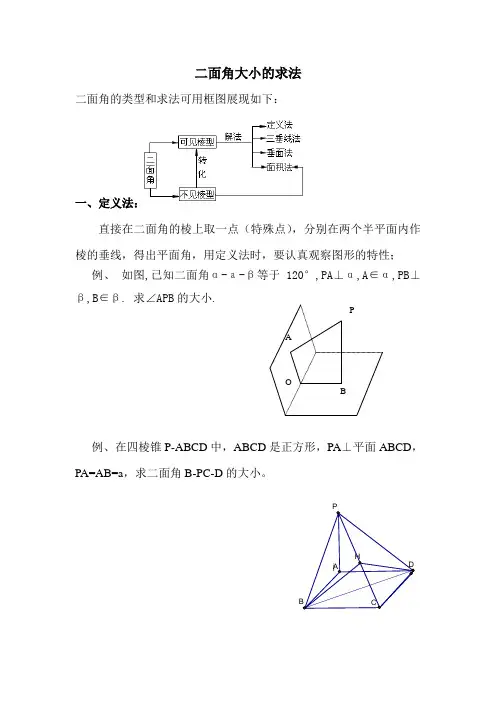
二面角大小的求法二面角的类型和求法可用框图展现如下：一、定义法：直接在二面角的棱上取一点（特殊点），分别在两个半平面内作棱的垂线，得出平面角，用定义法时，要认真观察图形的特性；例、如图,已知二面角α-а-β等于120°,PA⊥α,A∈α,PB⊥β,B∈β. 求∠APB的大小.PA=AB=a，求二面角B-PC-D的大小。
二、三垂线定理法：已知二面角其中一个面内一点到一个面的垂线，用三垂线定理或逆定理作出二面角的平面角；例、在四棱锥P-ABCD 中，ABCD 是平行四边形，PA ⊥平面ABCD ，PA=AB=a ，∠ABC=30°，求二面角P-BC-A 的大小。
例、(2003北京春)如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面C 1DE 与面CDE 所成二面角的正切值.ABCDA 1B 1C 1D 1EO例、ΔABC中，∠A=90°，AB=4，AC=3，平面ABC外一点P在平面ABC内的射影是AB中点M，二面角P—AC—B的大小为45°。
求（1）二面角P—BC—A的大小；（2）二面角C—PB—A的大小例、(2006年陕西试题)如图4，平面α⊥平面β，α∩β=l，A∈α，B∈β，点A在直线l上的射影为A1，点B在l的射影为B1，已知AB=2，AA1=1，BB1=2，求：二面角A1－AB－B1的大小.图4 B1AαβA1B LE F三、垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个半平面的交线所成的角即为平面角，由此可知，二面角的平面角所在的平面与棱垂直；例、空间的点P 到二面角βα--l 的面α、β及棱l 的距离分别为4、3、3392，求二面角βα--l 的大小.四、射影法：（面积法）利用面积射影公式S 射＝S 原cos θ,其中θ为平面角的大小，此方法不必在图形中画出平面角；例、在四棱锥P-ABCD 中，ABCD 为正方形，PA⊥平面ABCD ，PA ＝AB ＝a ，求平面PBA 与平面PDC 所成二面角的大小。
二面角的作与求求角是每年高考必考内容之一，可以做为选择题，也可作为填空题，时常作为解答题形式出现，重点把握好二面角，它一般出现在解答题中。
下面就对求二面角的方法总结如下：1、定义法：在棱上任取一点，过这点在两个面内分别引棱的垂线，这两条射线所成的角就是二面角的平面角。
2、三垂线定理及逆定理法：自二面角的一个面上的一点向另一个面引垂线，再由垂足向棱作垂线得到棱上的点。
斜足与面上一点连线，和斜足与垂足连线所夹的角即为二面角的平面角。
3、作棱的垂面法:自空间一点作与棱垂直的平面，截二面角的两条射线所成的角就是二面角的平面角。
4、投影法：利用s投影面=s被投影面θcos 这个公式对于斜面三角形，任意多边形都成立，是求二面角的好方法。
尤其对无棱问题5异面直线距离法： EF 2=m 2+n 2+d 2－2mn θcos例1：若p 是ABC ∆所在平面外一点，而PBC ∆和ABC ∆都是边长为2的正三角形，PA=6,求二面角P-BC-A 的大小。
分析：由于这两个三角形是全等的三角形， 故采用定义法解：取BC 的中点E ，连接AE 、PEAC=AB ，PB=PC ∴ AE ⊥ BC ，PE ⊥BC∴PEA ∠为二面角P-BC-A 的平面角在PAE ∆中AE=PE=3，PA=6PCBAE∴PEA ∠=90∴二面角P-BC-A 的平面角为900。
例2：已知ABC ∆是正三角形，⊥PA 平面ABC 且PA=AB=a,求二面角A-PC-B 的大小。
[思维]二面角的大小是由二面角的平面角 来度量的，本题可利用三垂线定理（逆）来作 平面角，还可以用射影面积公式或异面直线上两点 间距离公式求二面角的平面角。
解1：（三垂线定理法）取AC 的中点E ，连接BE ，过E 做EF ⊥PC,连接BF ⊥PA 平面ABC ，PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC ∴BE ⊥平面PAC由三垂线定理知BF ⊥PC∴BFE ∠为二面角A-PC-B 的平面角设PA=1,E 为AC 的中点，BE=23,EF=42 ∴tan BFE ∠=6=EFBE∴BFE ∠=arctan 6解2：（三垂线定理法）取BC 的中点E ，连接AE ，PE 过A 做AF ⊥PE, FM ⊥PC,连接FMAB=AC,PB=PC ∴ AE ⊥BC,PE ⊥BC∴ BC ⊥平面PAE,BC ⊂平面PBC∴平面PAE ⊥平面PBC, 平面PAE 平面PBC=PE由三垂线定理知AM ⊥PCPC BAEF MEPCBAF图1图2∴FMA ∠为二面角A-PC-B 的平面角设PA=1，AM=22,AF=721.=PE AE AP ∴sin FMA ∠=742=AM AF ∴FMA ∠=argsin742解3：（投影法）过B 作BE ⊥AC 于E,连结PE ⊥PA 平面ABC ，PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC ∴BE ⊥平面PAC∴PEC ∆是PBC ∆在平面PAC 上的射影设PA=1,则PB=PC=2,AB=141=∆PEC S ,47=∆PBC S由射影面积公式得，77cosarg ,77=∴==∆∆θθPBC PEC S S COS , 解4：（异面直线距离法）过A 作AD ⊥PC,BE ⊥PC 交PC 分别于D 、E 设PA=1,则AD=22,PB=PC=2 ∴BE=PC S PBC 21∆=414,CE=42,DE=42由异面直线两点间距离公式得 AB 2=AD 2+BE 2+DE 2-2ADBE θCOS ,θCOS =77cos arg ,77=∴θ [点评]本题给出了求平面角的几种方法，应很好掌握。
C A B DA A 1B DC C 1 B 1 解二面角问题（一）寻找有棱二面角的平面角的方法和求解。
（1）定义法：利用二面角的平面角的定义，在二面角的棱上取一点，过该点在两个半平面内作垂直于棱的射线，两射线所成的角就是二面角的平面角，这是一种最基本的方法。
要注意用二面角的平面角定义的三个“主要特征”来找出平面角，当然这种找出的角要有利于解决问题。
下面举几个例子来说明。
例1：如图，立体图形V －ABC 的四个面是全等的正三角形，画出二面角V －AB －C 的平面角并求出它的度数。
例2：在三棱锥P-ABC 中，∠APB=∠BPC=∠CPA=600，求二面角A-PB-C 的余弦值。
这样的类型是不少的，如下列几道就是利用定义法找出来的：1、在正方体ABCD －A 1B 1C 1D 1中，找出二面角B －AC －B 1的平面角并求出它的度数。
2、．边长为a 的菱形ABCD ，∠ACB=600，现沿对角线BD 将其折成才600的二面角，则A 、C 之间的距离为 。
（菱形两条对角线互相垂直，对折后的一条对角线成两条线段仍都垂直于另一条对角线，则所成的角是二面角的平面角）3、正三棱柱ABC —A 1B 1C 1的底面边长是4，过BC 的一个平面与AA 1交于D ，若AD =3，求二面角D ―BC ―A 的正切值。
总之，能用定义法来找二面角的平面角的，一般是图形的性质较好，能够较快地找到满足二面角的平面角的三个主要特征。
并且能够很快地利用图形的一些条件来求出所要求的。
在常见的几何体有正四面体，正三棱柱，正方体，以及一些平面图形，正三角形，等腰三角形，正方形，菱形等等，这些有较好的一些性质，可以通过它们的性质来找到二面角的平面角。
至于求角，通常是把这角放在一个三角形中去求解。
由图形及题目的已知条件来求这个三角形的边长或者角，再用解三角形的知识去求解。
（2）三垂线法：是利用三垂线的定理及其逆定理来证明线线垂直，来找到二面角的平面角的方法。
立体几何专题：二面角的四种求法一、二面角1、二面角的概念：从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，这两个半平面叫做二面角的面.2、二面角的平面角的概念：平面角是指以二面角的棱上一点为端点，在两个半平面内分别做垂直于棱的两条射线，这两条射线所成的角就叫做该二面角的平面角。
3、二面角的大小范围：[0°，180°] 二、求二面角大小的步骤是： （1）作：找出这个平面角；（2）证：证明这个角是二面角的平面角；（3）求：将作出的角放在三角形中，解这个三角形，计算出平面角的大小． 三、确定二面角的平面角的方法：1、定义法（棱上一点双垂线法）：提供了添辅助线的一种规律（1）方法：在二面角的棱上找一个特殊点，在两个半平面内分别过该点作垂直于棱的射线．（2）具体演示：如图所示，以二面角的棱a 上的任意一点O 为端点， 在两个面内分别作垂直于a 的两条射线OA ，OB ，则∠AOB 为此二面角的平面角2、三垂线法（面上一点双垂线法）----最常用（1）方法：自二面角的一个面上一点向另外一个面作垂线，再由垂足向棱作垂线得到棱上的点（即斜足），斜足和面上一点的连线与斜足和垂足的连线所夹的角，即为二面角的平面角（2）具体演示：在平面α内选一点A 向另一个平面β作垂线AB ，垂足为B ，再αβaOAB过点B 向棱a 作垂线BO ，垂足为O ，连接AO ，则∠AOB 就是二面角的平面角。
3、垂面法（空间一点垂面法）（1）方法：过空间一点作与棱垂直的平面，截二面角得两条射线，这两条射线所成的角就是二面角的平面角。
（2）具体演示：过二面角内一点A 作AB ⊥α于B ，作AC ⊥β于C ， 面ABC 交棱a 于点O ，则∠BOC 就是二面角的平面角。
4、射影面积法求二面角coss S射影（1）方法：已知平面β内一个多边形的面积为S ，它在平面α内的射影图形的面积为S射影，平面α和平面β所成的二面角的大小为θ，则COSθ=S射影S.这个方法对于无棱二面角的求解很简便。
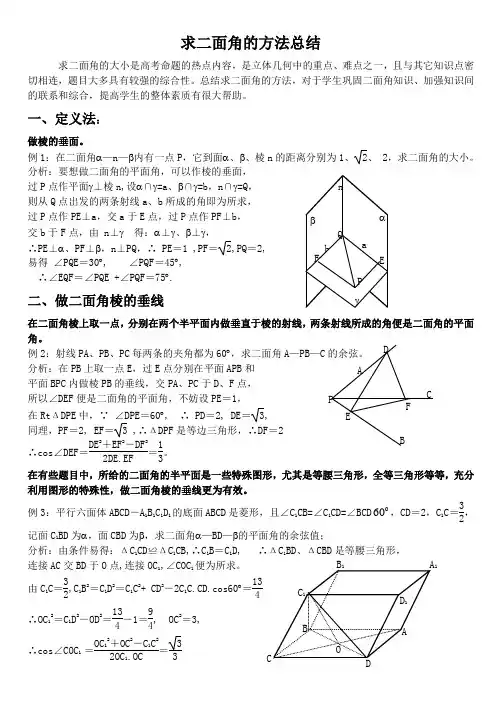
求二面角的方法总结求二面角的大小是高考命题的热点内容，是立体几何中的重点、难点之一，且与其它知识点密切相连，题目大多具有较强的综合性。
总结求二面角的方法，对于学生巩固二面角知识、加强知识间的联系和综合，提高学生的整体素质有很大帮助。
一、定义法：做棱的垂面。
例1：在二面角α—n —β内有一点P ，它到面α、β、棱n 的距离分别为1、2、 2，求二面角的大小。
分析：要想做二面角的平面角，可以作棱的垂面，过P 点作平面γ⊥棱n,设α∩γ=a 、β∩γ=b ，n ∩γ=Q ，则从Q 点出发的两条射线a 、b 所成的角即为所求， 过P 点作PE ⊥a ，交a 于E 点，过P 点作PF ⊥b ， 交b 于F 点，由 n ⊥γ 得：α⊥γ、β⊥γ， ∴PE ⊥α、PF ⊥β，n ⊥PQ ，∴ PE ＝1 ,PF ＝2,PQ ＝2, 易得 ∠PQE ＝30︒, ∠PQF ＝45︒, ∴∠EQF ＝∠PQE +∠PQF ＝75︒.二、做二面角棱的垂线在二面角棱上取一点，分别在两个半平面内做垂直于棱的射线，两条射线所成的角便是二面角的平面角。
例2：射线PA 、PB 、PC 每两条的夹角都为60︒，求二面角A —PB —C的余弦。
分析：在PB 上取一点E ，过E 点分别在平面APB 和 平面BPC 内做棱PB 的垂线，交PA 、PC 于D 、F 点，所以∠DEF 便是二面角的平面角，不妨设PE ＝1， 在Rt ΔDPE 中，∵ ∠DPE ＝60︒, ∴ PD ＝2, DE ＝3, 同理，PF ＝2, EF ＝ 3 ,∴ΔDPF 是等边三角形，∴DF ＝2∴cos ∠DEF ＝DE 2＋EF 2－DF 22DE.EF ＝13。
在有些题目中，所给的二面角的半平面是一些特殊图形，尤其是等腰三角形，全等三角形等等，充分利用图形的特殊性，做二面角棱的垂线更为有效。
例3：平行六面体ABCD －A 1B 1C 1D 1的底面ABCD 是菱形，且∠C 1CB=∠C 1CD=∠BCD60，CD ＝2，C 1C ＝32，记面C 1BD 为α，面CBD 为β，求二面角α—BD —β的平面角的余弦值；分析：由条件易得：ΔC 1CD ≌ΔC 1CB,∴C 1B ＝C 1D, ∴ΔC 1BD 、ΔCBD 是等腰三角形，连接AC 交BD 于O 点,连接OC 1,∠COC 1便为所求。
三垂线法求二面角1.直线与平面所成的角：平面的一条斜线和它在平面上的射影所成的角。
2.三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直3.三垂线定理的逆定理：如果平面内一条直线和穿过这个平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。
如图1，在二面角α—l一β中，过平面α内一点A作AO⊥平面β，垂足为O，过点O作OB⊥l于B(过A点作AB⊥于B)，连结AB(或OB)，由三垂线定理(或逆定理)知AB⊥l(或OB⊥l)，则∠ABO为二面角α—l—β的平面角．4.三垂线法三部曲（两垂一连）（1）作面的垂线（任一个半平面的垂线）（2）作棱的垂线（3）连线例1 已知斜三棱柱ABC—A1B1C1中，∠BCA=90°，AC=BC，A1在底面ABC 的射影恰为AC的中点M，又知AA1与底面ABC所成的角为60°．(1)求证：BC⊥平面AA1CC1；(2)求二面角B一AA1—C的正切值．例2 如图3，在底面是直角梯形的四棱锥S—ABCD中，∠ABC＝90°，SA1⊥面ABCD，SA=AB=BC＝1，AD＝2(1)求四棱锥S—ABCD的体积；(2)求面SCD与面SBA所成的二面角的正切值．例3.如图, 在△ABC中, AB⊥BC, SA⊥平面ABC, DE垂直平分SC, 且分别交AC,SC于D,E, 又SA=AB, SB=BC, 求二面角E-BD-C的大小.例4.已知在长方体ABCD－A1B1C1D1中，AB = 2，BC = BB1 =1 ，E为D1C1的中点，求二面角E－BD－C的大小．5．如图，三棱锥P-ABC的顶点P在底面ABC上的射影是底面Rt△ABC 斜边AC的中点O，若PB=AB=1，BC= √2，求二面角P-AB-C的正切值。
6. 已知M 是正方体ABCD －A 1B 1C 1D 1的棱AB 的中点，求二面角A 1－MC －A 的大小．7.在如图所示的空间几何体中,平面ACD ⊥平面ABC, AB=BC=CA=DA =DC=BE=2,BE 和平面ABC 所成的角为60度,且点E 在平面ABC 上的射影落在∠ABC 的平分线上(1).求证:DE//平面ABC ； (2).求二面角E －BC －A 的余弦值 O A B PC B CDE A 2 2 2 2 22。
高中立体几何中二面角求法摘要：在立体几何中，求二面角的大小是历届高考的热点，几乎每年必考，而对于求二面角方面的问题，同学们往往很难正确地找到作平面角的方法，本文对求二面角的方法作了一个总结，希望对学生有帮助。
（一）、二面角定义的回顾：从一条直线出发的两个半平面所组成的图形就叫做二面角。
二面角的大小是用二面角的平面角来衡量的。
而二面角的平面角是指在二面角βα--l 的棱上任取一点O ，分别在两个半平面内作射线l BO l AO ⊥⊥,，则AOB ∠为二面角βα--l 的平面角。
αβ(二)、二面角的通常求法 1、由定义作出二面角的平面角；*2、利用三垂线定理（逆定理）作出二面角的平面角；3、作二面角棱的垂面，则垂面与二面角两个面的交线所成的角就是二面角的平面角。
4、空间坐标法求二面角的大小5、平移或延长（展）线（面）法6、射影公式S 射影=S 斜面cos θ7、化归为分别垂直于二面角的两个面的两条直线所成的角1、利用定义作出二面角的平面角，并设法求出其大小。
例1、 如图,已知二面角α-а-β等于120°,PA ⊥α,A ∈α,PB ⊥β,B ∈β. 求∠APB 的大小.解: 设平面∩PAB α=OA,平面PAB ∩β=OB 。
∵PA ⊥α, аα ∴PA ⊥а同理PB ⊥а ∴а⊥平面PAB又∵OA 平面PAB ∴а⊥OA同理а⊥OB.∴∠AOB 是二面角α-а-β的平面角. 在四边形PAOB 中, ∠AOB=120°,.OAB)AB lP.BA∠PAO=∠POB=90°, 所以∠APB=60° 2、 （3、三垂线定理（逆定理）法由二面角的一个面上的斜线（或它的射影）与二面角的棱垂直，推得它位于二面角的另一的面上的射影（或斜线）也与二面角的棱垂直，从而确定二面角的平面角。
例2：如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面C 1DE 与面CDE 所成二面角的正切值.解：在长方体ABCD —A 1B 1C 1D 1中 由三垂线定理可得： CD CE=1, DE=53、找（作）公垂面法由二面角的平面角的定义可知两个面的公垂面与棱垂直，因此公垂面与两个面的交线所成的角，就是二面角的平面角。
例5、如图，已知PA 与正方形ABCD 所在平面垂直，且AB ＝PA ，求平面PAB 与平面PCD 所成的二面角的大小。
\解: ∵PA ⊥平面ABCD ，∴PA ⊥CD ．P又CD ⊥AD ，故CD ⊥平面PAD ． A D 而CD平面PCD ， B C所以 平面PCD ⊥平面PAD ．ABCDA 1B 1C 1（EOCODE O C C ，连结，作过点⊥11DECO ⊥的平面角为二面角C DE C OC C --∠∴11的正方形是边长为又2ABCD CODE CE CD S CDE Rt CDE ⋅=⋅=∆∆2121中，在11=CC 又552tan 1=∠∴OC C 552tan arg 1=∠∴OC C 552=∴CO同理可证 平面PAB ⊥平面PAD ．因为 平面PCD ∩平面PAD ＝PD ，平面PAB ∩平面PAD ＝PA ，所以PA 、PD 与所求二面角的棱均垂直，即∠APD 为所求二面角的平面角，且∠APD ＝45°．5、平移或延长（展）线（面）法将图形中有关线段或平面进行平移或延长（展），以其得到二面角的两个平面的交线。
~例3、正三角形ABC 的边长为10，A ∈平面α，B 、C 在平面α的同侧，且与α的距离分别是4和2，求平面ABC 与α所成的角的正弦值。
解：设E 、F 分别为B 、C 的射影，连EF 并延长交BC 延长线于D ，连AD ；AE ∵E 、F 是B 、C 射影 ∴BE 丄α； ∵CF 丄α ∴BE ∥CF 又CF ：BE=21，∴C 是BD 的中点 ∴BC=DC ， ∵ΔABC 是正三角形∴∠B=∠BCA=∠BAC=60°， 又∠ACB+∠ACD=180° ， ∴∠ACD=120°又AC=DC ， ∴∠CAD=∠CDA=30°，又∠BAD=∠BAC+∠CAD ，】∴∠BAD=90°，∴BA 丄AD ，又∵AE 是AB 在平面α上的射影，∴AE ⊥AD 又 BA ⊥AD ，平面ABC ∩平面α=A ， ∴∠BAE 是平面ABC 与α所成的角，∴BE ⊥平面α，∴ BE ⊥AE ， ∴ΔABC 是 Rt ΔSin ∠BAE=BE ：AB=52，即平面ABC 与α所成角的正弦值为52。
6、射影公式由公式S 射影=S 斜面cos θ，作出二面角的平面角直接求出。
运用这一方法的关键是从图中找出斜面多边形和它在有关平面上的射影，而且它们的面积容易求得。
例4、如图，设M 为正方体ABCD-A 1B 1C 1D 1的棱CC 1的中点，求平面BMD 与底面ABCD 所成的二面角的大小。
解：∵D 1D ⊥面ABCD ，C 1C ⊥面ABCD ，∴ ∆BMD 1在底面上的射影为∆BDC ，.设正方体的棱长a ，则S ∆BCD =21a 2，BD 1=3a所以∴MH=22a ，S ∆BMD1=46a 2由S ∆BDC =S ∆BMD1cos θ得θ=arccos367、化归为分别垂直于二面角的两个面的两条直线所成的角例6、在长方体ABCD －A 1B 1C 1D 1中，点E 、F 分别在BB 1、DD 1上，且AE ⊥A 1B ，AF ⊥A 1D ． (1) 求证:A 1C ⊥平面AEF ；若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角)，则在空间中有定理：“若两条直线分别垂直于两个平面，则这两条直线所成的角与这两个平面所成角的大小相等．”（2）、试根据上述定理，在AB ＝4，AD ＝3，AA 1＝5时，求平面AEF 与平面D 1B 1BD 所成角的大小的余弦值解：(1)∵A 1B ⊥BC 即A 1B 是A 1C 的射影又∵A 1B ⊥AE ∴A 1C ⊥AE 同理 A 1C ⊥AF ∴A 1C ⊥平面AEF (2) 的解法如下： 过C 作BD 的垂线交AB 于G ．又D 1D ⊥CG ，故CG ⊥平面BB 1D 1D ．# BCD A 1 B 1C 1D 1 FE；而A 1C ⊥平面AEF((1)已证)，设CG 与A 1C 所成的角为α，则α即为平面BB 1D 1D 与平面AEF 所成的角．Sin ∠BCG ＝Sin ∠ABD ＝53，，Cos ∠BCG ＝54，GC ＝415 BG=49，AG=47A 1G 2=A 1A 2+AG 2=16449，A 1C 2=AB 2+AD 2+AA 1 2=50 。
在∆A 1CG 中，由余弦定理得Cos ∠A 1CG=25212求二面角的大小还有很多的方法，这里只是列举了几个常用的方法，希望同学们能在解题的时候加以总结，争取在高考中旗开得胜！如何用空间向量求解二面角求解二面角大小的方法很多，诸如定义法、三垂线法、垂面法、射影法、向量法等若干种。
而这些方法中最简单易学的就是向量法，但在实际教学中本人发现学生利用向量法求解二面角还是存在一些问题，究其原因应是对向量法的源头不尽了解。
本文就简要介绍有关这类问题的处理方法，希望对大家有所帮助。
在立体几何中求二面角可归结为求两个向量的夹角问题．对于空间向量→a 、→b ，有cos ＜→a ，→b＞=→→→→⋅⋅||||b a ba ．利用这一结论，我们可以较方便地处理立体几何中二面角的问题．例1 在四棱锥V-ABCD 中，底面ABCD 是正方形，侧面VAD 是正三角形，平面VAD ⊥底面ABCD ．求面VAD 与面VDB 所成的二面角的余弦值．证明： 建立如图空间直角坐标系，并设正方形边 长为1，依题意得AB −−→= (0，1，0)，是面VAD 的法向量， 设n →= (1，y ，z)是面VDB 的法向量，则0,0.n VB n VB →−−→→−−→⎧⋅=⎪⎨⎪⋅=⎩⇒1,y z =-⎧⎪⎨=⎪⎩⇒n →= (1，－1，－3)。
∴cos ＜AB −−→，n →＞||||AB nAB n −−→→−−→→⋅⋅=－7， ！又由题意知，面VAD 与面VDB例2如图，直三棱柱ABC —A 1B 1C 1中，∠ACB =90︒，AC=1，CB=2，侧棱AA 1=1，侧面AA 1B 1B 的两条对角线交点为D ，B 1C 1的中点为M ．、⑴求证CD ⊥平面BDM ；⑵求面B 1BD 与面CBD 所成二面角的余弦值．解：⑴略⑵如图，以C 为原点建立坐标系.设BD 中点为G ，连结B 1G ，则依G(4，14，14)，BD −−→= (－2，12，12)，1B G −−→= (－4，－34，14)，∴BD −−→·1B G −−→= 0，∴BD ⊥B 1G ．又CD ⊥BD ，∴CD −−→与1B G −−→的夹角θ等于所求二面角的平面角．∴ cos θ=11||||CD B G CD B G −−→−−→−−→−−→⋅⋅=－3． 例3如图，在四棱锥P —ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD=DC ，E 是PC 的中点，作EF ⊥PB 交PB 于点F ．求二面角C —PB —D 的大小：解：如图所示建立空间直角坐标系，D 为坐标原点，设a DC =设点F 的坐标为000()x y z ，，，PA −−→=PB λ−−→，则000()()x y z a a a a λ-=-，，，，．从而000(1)x a y a z a λλλ===-，，．所以PE −−→=00011(,,)(,(),())2222a a x y z a a a λλλ---=---．由条件EF ⊥PB 知，PE −−→·PB −−→= 0，即yBB 1C 1A 1CADMx0)21()21(222=---+-a a a λλλ，解得31=λ．∴点F 的坐标为2()333a a a，，，且()366a a a PE −−→=--，，，2()333a a a FD −−→=---，，， ∴PB −−→·FD −−→22220333a a a =--+=，即FD PB ⊥，故EFD ∠是二面角C —PB —D 的平面角． ∵PE −−→·FD −−→=222291896a a a a =-+=，且||PE −−→==，||FD a −−→==，∴21cos 2||||63a PE FDEFD PE FD −−→−−→−−→−−→⋅∠===，∴3π=∠EFD ． 所以，二面角C —PB —D 的大小为3π． 例 4 已知三棱柱OAB —1O A 1B 1中，平面11O OBB ⊥平面OAB ，∠AOB =︒90，∠OB O 1=︒60，且OB =1OO = 2，OA =3，求二面角1O —AB—O 的余弦值．解：以O 为原点，分别以OA ，OB 所在的直线为x ，y 轴，过O 点且与平面AOB 垂直的直线为z 轴，建立空间直角坐标系．如图，则O (0，0，0)，1O (0，1，3)，A(3，0，0)，1A (3，1，3)，B(0，2，0)．∴−→−1AO = (－3，1，3)，−→−AB = (－3，2，0)． 显然−→−OZ 为平面AOB 的法向量，取→1n = (0，0，1)，设平面AB O 1的法向量为→2n = (x ，y ，z)，则→2n ·−→−1AO = 0，→2n ·−→−AB = 0．即⎪⎩⎪⎨⎧=+-=++-023033y x z y x ，令y =3，x = 2，z = 1，则→2n = (2，3，1)．∴cos ＜→1n ，→2n ＞=||||2121→→→→⋅⋅n n n n =221=42， 故二面角1O —AB —O 的余弦值是42。
