曲线论复习

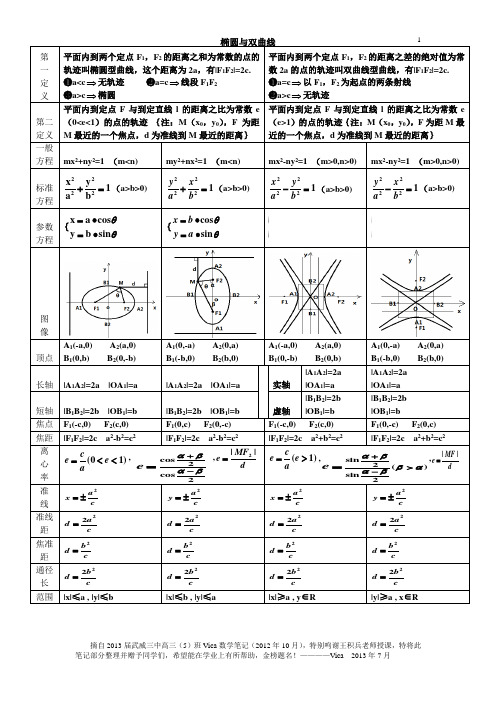
椭圆与双曲线1第 一 定 义平面内到两个定点F 1，F 2的距离之和为常数的点的轨迹叫椭圆型曲线，这个距离为2a ，有|F 1F 2|=2c. ❶a<c ⇒无轨迹 ❷a=c ⇒线段F 1F 2 ❸a>c ⇒椭圆平面内到两个定点F 1，F 2的距离之差的绝对值为常数2a 的点的轨迹叫双曲线型曲线，有|F 1F 2|=2c. ❶a=c ⇒以F 1，F 2为起点的两条射线 ❷a>c ⇒无轨迹第二定义 平面内到定点F 与到定直线l 的距离之比为常数e （0<e<1）的点的轨迹 ｛注：M （x 0，y 0），F 为距M 最近的一个焦点，d 为准线到M 最近的距离｝ 平面内到定点F 与到定直线l 的距离之比为常数e（e>1）的点的轨迹｛注：M （x 0，y 0），F 为距M 最近的一个焦点，d 为准线到M 最近的距离｝ 一般方程 mx 2+ny 2=1 （m<n) my 2+nx 2=1 （m<n)mx 2-ny 2=1 （m>0,n>0)mx 2-ny 2=1 （m>0,n>0)标准方程1b y a x 2222=+（a>b>0) 12222=+b x a y （a>b>0) 12222=-b y a x （a>b>0) 12222=-b x a y （a>b>0) 参数方程θθsin b y cos a x ∙=∙=｛θθsin cos ∙=∙=a y b x ｛图 像顶点 A 1(-a,0) A 2(a,0)B 1(0,b) B 2(0,-b) A 1(0,-a) A 2(0,a) B 1(-b,0) B 2(b,0) A 1(-a,0) A 2(a,0) B 1(0,-b) B 2(0,b) A 1(0,-a) A 2(0,a) B 1(-b,0) B 2(b,0) 长轴 |A 1A 2|=2a |OA 1|=a |A 1A 2|=2a |OA 1|=a 实轴 |A 1A 2|=2a |OA 1|=a |A 1A 2|=2a |OA 1|=a 短轴 |B 1B 2|=2b |OB 1|=b |B 1B 2|=2b |OB 1|=b 虚轴|B 1B 2|=2b |OB 1|=b|B 1B 2|=2b |OB 1|=b焦点 F 1(-c,0) F 2(c,0) F 1(0,c) F 2(0,-c) F 1(-c,0) F 2(c,0) F 1(0,-c) F 2(0,c) 焦距 |F 1F 2|=2c a 2-b 2=c 2 |F 1F 2|=2c a 2-b 2=c 2|F 1F 2|=2c a 2+b 2=c 2|F 1F 2|=2c a 2+b 2=c 2离 心 率 )10(<<=e ace ,2cos2cos βαβα-+=e ,d MF e ||2=)1(>=e a c e ,)(2sin2sin αββαβα>-+=e ,dMF e ||=准 线 c a x 2±=c a y 2±= c a x 2±=c a y 2±= 准线距 ca d 22=ca d 22=ca d 22=ca d 22=焦准距 c b d 2=c bd 2=c bd 2=c bd 2=通径长cb d 22= cb d 22= cb d 22= cb d 22=范围 |x|≤a , |y|≤b |x|≤b , |y|≤a |x|≥a , y ∈R |y|≥a , x ∈R椭圆与双曲线2一些其他结论：Ⅰ. 以焦点为圆心，以它到曲线上任意一点为半径的圆和对应准线的位置关系： ❶ 对于椭圆：相离 ❷ 对于双曲线：相交Ⅱ. 以曲线上任意一点为圆心，以它到准线距离为半径的圆和对应焦点的位置关系： ❶ 对于椭圆：在圆内 ❷ 对于双曲线：在圆外 ❸对于抛物线：在圆上焦 半 径 |MF 1|=a + e ·x 0 |MF 2|=a - e ·x 0 |MF 1|=a + e ·y 0 |MF 2|=a - e ·y 0左支：|MF 1|= -（ex 0+a ） |MF 2|= -（ex 0 - a ） 右支：|MF 1|= ex 0+a |MF 2|= ex 0 - a上支：|MF 1|= ey 0+a |MF 2|= ey 0 - a 下支：|MF 1|= -（ey 0+a ） |MF 2|= -（ey 0 - a ）焦点弦 过左焦点：2a+e （x 1+x 2） 过右焦点：2a-e （x 1+x 2） 过上焦点：2a-e （y 1+y 2） 过下焦点：2a+e （y 1+y 2） 过左焦点：-2a-e （x 1+x 2） 过右焦点：-2a+e （x 1+x 2） 过上焦点：-2a+e （y 1+y 2） 过下焦点：-2a-e （y 1+y 2）弦长 ||1212x x k d -+=||1212y y k d -+=-||1212x x k d -+=||1212y y k d -+=-焦点三角形S 2tan221θ∙=∆b S F MF 2tan221θ∙=∆b S F MF 2cot221θ∙=∆b S F MF 2cot221θ∙=∆b S F MF 共离心率方程 )0(2222>=+λλby a x )0(2222>=+λλb x a y 共渐近线方程λ=2222-b y a x )0(,-2222≠=λλbx a y 渐近线x ab y ±= y ab x ±= 点P （x ，y ）与曲线的关系带入方程，若方程 （在曲线内）（在曲线上）在曲线外）(111<=> 带入方程，若方程 （在曲线内）（在曲线上）在曲线外）(111<=>。

2019年高考政治复习曲线题专题复习总结一、流通中需要的货币量与商品和服务的价格成正比，与货币流通速度成反比。

用坐标曲线图表示：二、人民币升值有利于进口，但不利于出口。

用坐标曲线图表示：三、用曲线图理解价格的变化1）价值决定价格商品价格由价值(社会必要劳动时间)决定，随着社会劳动生产率的变化而变化。

1、价值决定价格不考虑其他因素的情况下，商品价值越大，价格越高。

2社会劳动生产率与价格商品价值量与社会劳动生产率成反比，不考虑其他因素的情况下，社会劳动生产率越高，商品价值量越低，价格越低。

四、价格变动对人们生活的影响1、一般情况下，价格与需求量的变化呈反方向变动，即当某种商品价格上升时，人们会减少对它的购买；当某种商品价格下降时，人们会增加对它的购买。

2、不同商品对价格变动的反映程度不同。

价格变动对生活必需品(A)需求量的影响比较小，对高档耐用品(B)需求量的影响比较大。

3、相关商品价格的变动会影响消费者对既定商品的需求1）互为替代品（甲价格与互为替代品乙的需求量同向变动）2）互补商品（甲价格与互补商品的乙需求量反向变动）五、价格变动对生产的影响当某种商品价格上涨，生产者获利增加，会扩大生产规模，增加产量(供给)；某种商品价格下降，获利减少，生产者会压缩生产规模，减少产量(供给)。

六、用曲线图理解收入和消费的关系1、收入(当前收入和未来预期收入)越高，消费水平越高，二者成正比。

2、收入差距越大，社会总体消费水平越低。

二者成反比。

3、收入水平越高，恩格尔系数越小。

二者成反比。

七、【曲线特点】根据需求法则，若以需求价格为纵轴，需求数量为横轴，那么需求曲线就是一条向右下方倾斜的曲线。

如图一所示，当商品的价格由P1下降到P2时，需求量由Q1增加到Q2。

【知识拓展】在商品本身价格不变的情况下，由其他因素（如人们的收入，相关商品的价格，人们的偏好，消费风气等）变动所引起的需求量的变动，表现为整条需求曲线的移动，即需求增加，需求曲线向右平移；需求减少，需求曲线向左平移。

§2 向量函数一 向量函数的定义定义 G 是一点集，若对每一个x €G ，有确定的向量r 与之对应，则称在G 上给定了一个向量函数。

记作(),r r x x G =∈。

若G 为区间，则G 中的点为实数t ，这时()r r t = 为一元向量函数；()r t终点的轨迹是一条曲线。

若G 为平面域，则x €G ，x=x(u,v), 这时()(,)r r x r u v ==为二元向量函数。

()r x终点的轨迹是曲面。

向量函数可以用分量表示，它们的分量是三个实函数，(){(),(),()}r r t x t y t z t ==，(,){(,),(,),(,)}r u v x u v y u v z u v = 。

二 向量函数的积分A. 123若r(t)=x(t)e +y(t)e +z(t)e ，则()bar t dt ⎰⎰⎰⎰b b b 123aaa=e x(t)dt+e y(t)dt+e z(t)dtB. ,()()()cb c aaba b c r t dt r t dt r t dt <<+⎰⎰⎰=C. m 是常数时，()()bb a amr t dt m r t dt=⎰⎰。

D. ()()b b a a m mr t dt m r t dt=⎰⎰是常向量时，.E. ()()b b a a m m r t dt m r t dt⨯=⨯⎰⎰ 是常向量时，.F.[()]()x ar t dt r x =⎰d dx .三 两个重要命题①命题1 向量函数()r t 具有固定长⇔对于t 的每一个值，()()0()()r t r t r t r t ''⋅=⇔与垂直。

② 向量函数()r t 对于它的变量t 的旋转速度给定()r r t = ，给t 一增量t ∆，((),()),lim tr t r t tϕϕ∆∆=∠+∆ 则极限||叫做向量函数()r t对于它的变量t 的旋转速度。

高三复习数学双曲线知识点推论在高中数学的学习中，双曲线是一个重要的知识点。

双曲线不仅在几何学中有着广泛的应用，而且在物理学和工程学中也有着重要的地位。

高三学生即将面临数学高考，这时候复习双曲线的知识点和推论就显得尤为关键。

双曲线是一类特殊的曲线，其定义是在平面上选取两个不相交的直线l1和l2作为双曲线的渐近线，然后取一个定点F（称为焦点），对于双曲线上的任意一点M，其到焦点F的距离与到直线l1的距离之差等于到直线l2的距离之差。

数学中常用的双曲线有两种，分别是正双曲线和负双曲线。

首先，我们来讨论一下双曲线的基本性质。

正双曲线的两个渐近线之间的距离是一个常数，我们称之为双曲线的长轴。

长轴的一半称为双曲线的半长轴。

正双曲线的焦点到中心的距离称为焦距。

对于负双曲线，定义同样适用，只是焦点到中心的距离是负值。

这些概念在解题时非常重要，可以帮助我们快速确定双曲线的一些性质。

双曲线还有一个重要的性质是对称性。

以双曲线的中心为原点，双曲线的对称轴对于双曲线上的任意一点M，M关于对称轴的对称点M'仍然在双曲线上。

这个性质可以方便我们求解一些求对称点坐标的问题。

另外，双曲线还有一个重要的应用就是求解双曲线的标准方程。

对于给定的双曲线，我们可以通过已知焦点、渐近线或者顶点等信息来确定双曲线的方程。

这在高考中也是一个常考的问题。

记住双曲线的标准方程和相关的公式是非常有必要的。

除了基本性质和标准方程，我们在学习双曲线时还需要了解一些重要的推论。

其中一条重要的推论是双曲线的渐近斜率。

对于一条正双曲线，其渐近斜率等于±b/a，其中a和b分别表示双曲线的半长轴和半焦距。

这个推论的应用广泛，可以方便我们在图中确定渐近线的方程。

双曲线的离心率也是一个重要的推论。

对于正双曲线，离心率的定义是e=c/a，其中c表示焦距，a表示半长轴。

离心率可以帮助我们判断双曲线的形状，并在解题时起到重要作用。

在解题中，我们还可以通过双曲线的性质和推论来求解一些问题。

第一章 曲线论一、知识重点：1．定理：设r ()t 是非零连续可微的向量函数，则有： (1) r ()t 具有固定长 ⇔ r ()t ∙ r /()t =0 (2) r ()t 具有固定方向 ⇔ r ()t ⨯r /()t =0(3) r ()t 平行于固定平面 ⇔ （ r ()t ，r /()t ，r //()t ）=0 2．旋转速度：单位向量函数r ()t （即 |r ()t |=1 ）关于t 的旋转速度等于其微商的模 | r /()t |。

3. 正常点：给出C 1类得曲线r=r ()t ,假设对于曲线r=r ()t 上一点（t=t 0）有 r /()t ≠0，则这一点称为曲线的 正常点。

例：平面曲线r ()t ={}23,t t 求r ()t 是不是正则曲线？ 解： r /()t ={}t t 2,32，当t=0时，r /()t =0 ∴ r ()t 不是正则曲线。

4. 坐标表示的 切线方程 的公式：()()0/0t x t x X -=()()0/t y t y Y -=()()0/t z t z Z -例：求圆柱螺线r ()t =}{bt t a t a ,sin ,cos 在t=3π处的切线方程。

解： r ()t =}{bt t a t a ,sin ,cos 有r /()t =}{b t a t a ,cos ,sin - 在t=3π时，有 r ⎪⎭⎫⎝⎛3π=⎭⎬⎫⎩⎨⎧b a a 3,23,2π r /⎪⎭⎫ ⎝⎛3π=⎭⎬⎫⎩⎨⎧-1,2,23b a a ∴切线方程为a a X 232--=223a a Y -=bbZ 3π-5. 坐标表示的 法面方程 的公式：()[]0t x X -x /()0t +()[]0t y Y -y /()0t +()[]0t z Z -z /()0t =0例：求圆柱螺线r ()t =}{bt t a t a ,sin ,cos 在t=6π处的法面方程。

第一章 曲线论§2 向量函数5. 向量函数)(t r 具有固定方向的充要条件是)(t r × )('t r= 0 ;分析：一个向量函数)(t r 一般可以写成)(t r =)(t λ)(t e 的形式,其中)(t e为单位向量函数,)(t λ为数量函数,那么)(t r 具有固定方向的充要条件是)(t e 具有固定方向,即)(t e为常向量,因为)(t e的长度固定;证 对于向量函数)(t r ,设)(t e 为其单位向量,则)(t r =)(t λ)(t e ,若)(t r具有固定方向,则)(t e 为常向量,那么)('t r =)('t λe ,所以 r ×'r=λ'λe ×e =0 ;反之,若r ×'r =0 ,对)(t r =)(t λ)(t e 求微商得'r ='λe +λ'e ,于是r×'r =2λe ×'e =0 ,则有 λ =0 或e ×'e =0 ;当)(t λ= 0时,)(t r =0 可与任意方向平行；当λ≠0时,有e ×'e=0,而e×'e2)=22'e e -e ·'e 2)＝2'e ,因为e 具有固定长,e ·'e = 0 ,所以 'e =0 ,即e为常向量;所以,)(t r 具有固定方向;6．向量函数)(t r平行于固定平面的充要条件是r 'r ''r =0 ;分析：向量函数)(t r 平行于固定平面的充要条件是存在一个定向向量)(t n ,使)(t r ·n= 0 ,所以我们要寻求这个向量n 及n 与'r ,''r的关系;证 若)(t r 平行于一固定平面π,设n 是平面π的一个单位法向量,则n为常向量,且)(t r·n = 0 ;两次求微商得'r ·n = 0 ,''r ·n = 0 ,即向量r ,'r ,''r 垂直于同一非零向量n,因而共面,即r 'r ''r =0 ;反之, 若r 'r ''r =0,则有r ×'r =0 或r ×'r ≠0 ;若r ×'r =0,由上题知)(t r 具有固定方向,自然平行于一固定平面,若r ×'r≠0 ,则存在数量函数)(t λ、)(t μ,使''r =r λ+μ'r①令n =r ×'r,则n≠0 ,且)(t r ⊥)(t n ;对n =r ×'r求微商并将①式代入得'n =r ×''r =μr ×'r=μn ,于是n ×'n =0 ,由上题知n 有固定方向,而)(t r ⊥n ,即)(t r 平行于固定平面;§3 曲线的概念1．求圆柱螺线x =t cos ,y =t sin ,z=t 在1,0,0的切线和法平面;解 令t cos =1,t sin =0, t =0得t =0, 'r0={ -t sin ,t cos ,1}|0=t ={0,1,1},曲线在0,1,1的切线为 111z y x ==- ,法平面为 y + z = 0 ;2．求三次曲线},,{32ct bt at r =在点0t 的切线和法平面;解 }3,2,{)('2000ct bt a t r = ,切线为230020032ct ct z bt bt y a at x -=-=-, 法平面为 0)(3)(2)(30202000=-+-+-ct z ct bt y bt at x a ; 3. 证明圆柱螺线r ={ a θcos ,a θsin ,θb } +∞∞- θ的切线和z 轴作固定角;证明 'r= {-a θsin ,a θcos ,b },设切线与z 轴夹角为ϕ,则ϕcos=22||||'ba be r k r +=⋅ 为常数,故ϕ为定角其中k 为z 轴的单位向量; 4. 求悬链线r ={t ,a t a cosh }-∞∞ t 从t =0起计算的弧长;解'r = {1,atsinh },|'r | =at2sinh 1+ = a tcosh , ｓ＝a tta ta dt sinh cosh=⎰ ;９．求曲线2232,3axz y a x ==在平面3ay =与y = 9a 之间的弧长;解 曲线的向量表示为r ＝}2,3,{223xa a x x ,曲面与两平面3a y = 与y = 9a 的交点分别为x=a 与x=3a , 'r ＝}2,,1{2222xa ax -,｜'r ｜＝444441x a a x ++＝22222xa a x +,所求弧长为a dx xa a x s aa9)2(22322=+=⎰; 10. 将圆柱螺线r ={a t cos ,a t sin ,b t }化为自然参数表示;解 'r= { -a t sin ,a t cos ,b},s = t b a dt r t 220|'|+=⎰ ,所以22ba s t +=,代入原方程得 r ={a cos22ba s +, a sin22ba s +,22ba bs +}11.求用极坐标方程)(θρρ=给出的曲线的弧长表达式; 解由θθρcos )(=x ,θθρsin )(=y 知'r ={)('θρθcos -θθρsin )(,)('θρθsin +θθρcos )(},|'r| = )(')(22θρθρ+,从0θ到θ的曲线的弧长是s=⎰θθ0)(')(22θρθρ+d θ ;§4 空间曲线1．求圆柱螺线x =a t cos ,y =a t sin ,z = b t 在任意点的密切平面的方程;解 'r ={ -a t sin ,a t cos ,b},''r={-a t cos ,- a t sin ,0 } 所以曲线在任意点的密切平面的方程为sin cos cos sin sin cos ta ta b t a t a bt z t a y t a x ------ = 0 ,即b t sin x-b t cos y+a z-ab t=0 .2. 求曲线r = { t t sin ,t t cos ,t t e } 在原点的密切平面、法平面、从切面、切线、主法线、副法线;解 原点对应t=0 , 'r0={ t sin +t t cos ,t cos - t t sin ,t e +t t e 0}=t ={0,1,1},=)0(''r{2t cos + t t cos ,t cos - t t sin ,2t e +t t e 0}=t ={2,0,2} ,所以切线方程是110zy x == ,法面方程是 y + z = 0 ； 密切平面方程是202110zy x=0 ,即x+y-z=0 ,主法线的方程是⎩⎨⎧=+=-+00z y z y x 即112zy x =-=； 从切面方程是2x-y+z=0 ,副法线方程式111-==zy x ; 3．证明圆柱螺线x =a t cos ,y =a t sin ,z = b t 的主法线和z 轴垂直相交;证 'r ={ -a t sin ,a t cos ,b}, ''r ={-a t cos ,- a t sin ,0 } ,由'r ⊥''r 知''r为主法线的方向向量,而''r 0=⋅k所以主法线与z 轴垂直；主法线方程是与z 轴有公共点o,o,bt;故圆柱螺线的主法线和z 轴垂直相交;4.在曲线x = cos αcost ,y = cos αsint , z = tsin α的副法线的正向取单位长,求其端点组成的新曲线的密切平面;解 'r = {-cos αsint, cos αcost, sin α } , ''r={ -cos αcost,- cos αsint ,0 }=⨯⨯=|'''|'''r r r rγ{sin αsint ,- sin αcost , cos α }新曲线的方程为r ={ cos αcost + sin αsint ,cos αsint- sin αcost ,tsin α + cos α }对于新曲线'r={-cos αsint+ sin αcost ,cos αcost+ sin αsint,sin α }={sin α-t,cos α-t, sin α} , ''r={ -cos α-t, sin α-t,0} ,其密切平面的方程是即 sin α sint-α x –sin α cost-α y + z – tsin α – cos α = 0 .5．证明曲线是球面曲线的充要条件是曲线的所有法平面通过一定点; 证 方法一：⇒设一曲线为一球面曲线,取球心为坐标原点,则曲线的向径)(t r具有固定长,所以r ·'r= 0,即曲线每一点的切线与其向径垂直,因此曲线在每一点的法平面通过这点的向径,也就通过其始点球心;⇐ 若一曲线的所有法平面通过一定点,以此定点为坐标原点建立坐标系,则r ·'r = 0,)(t r具有固定长,对应的曲线是球面曲线;方法二：()r r t =是球面曲线⇔存在定点0r 是球面中心的径矢和常数R 是球面的半径使220()r r R -=⇔02()0r r r '-⋅= ,即0()0r r r '-⋅= ﹡而过曲线()r r t =上任一点的法平面方程为()0r r ρ'-⋅= ;可知法平面过球面中心⇔﹡成立;所以,曲线是球面曲线的充要条件是曲线的所有法平面通过一定点;6.证明过原点平行于圆柱螺线r ={a t cos ,a t sin ,b t }的副法线的直线轨迹是锥面2222)(bz y x a =+.证 'r={ -a tsin ,a t cos , }, ''r ={-a t cos ,- a t sin ,0 } ,'r×''r=},cos ,sin {a t b t b a ---为副法线的方向向量,过原点平行于副法线的直线的方程是az t b y t b x =-=cos sin ,消去参数t 得2222)(bz y x a =+; 7．求以下曲面的曲率和挠率⑴ },sinh ,cosh {at t a t a r =,⑵ )0)}(3(,3),3({323a t t a at t t a r +-=;解 ⑴},cosh ,sinh {'a t a t a r =,}0,sinh ,cosh {''t a t a r =,}0,cosh ,{sinh '''t t a r =,}1,cosh ,sinh {'''--=⨯t t a r r,所以t a t a t a r r r k 2323cosh 21)cosh 2(cosh 2|'||'''|==⨯= ta t a a r r r r r 22422cosh 21cosh 2)'''()''','','(==⨯=τ ; ⑵ }1,2,1{3'22t t t a r +-= ,}1,0,1{6'''},,1,{6''-=-=a r t t a r,'r ×''r =}1,2,1{18222+--t t t a ,22322223)1(31)1(2227)1(218|'||'''|+=++=⨯=t a t a t a r r r k22224232)1(31)1(2182618)'''()''','','(+=+⨯⨯⨯=⨯=t a t a a r r r r r τ ; 8．已知曲线}2cos ,sin ,{cos 33t t t r = ,⑴求基本向量γβα ,,；⑵曲率和挠率；⑶验证伏雷内公式;分析 这里给出的曲线的方程为一般参数,一般地我们可以根据公式去求基本向量和曲率挠率,我们也可以利用定义来求;解 ⑴ }4,sin 3,cos 3{cos sin }2sin 2,cos sin 3,sin cos 3{'22--=--=t t t t t t t t t r,,cos sin 5|)('|t t t r dtds ==设sintcost>0, 则}54,sin 53,cos 53{|'|'--==t t r r α,}0,cos 53,sin 53{cos sin 51t t t t ds dt dt d ==•αα, }0,cos ,{sin ||t t ==••ααβ,}53,sin 54,cos 54{--=⨯=t t βαγ ,⑵ t t k cos sin 253||==•α,}0,cos ,sin {cos sin 254t t t t --=•γ ,由于•γ 与β 方向相反,所以 tt cos sin 254||==•γτ⑶ 显然以上所得 τγβα,,,••k 满足 βτγβα -==••,k ,而γτακβ+-=-=•}0,sin ,{cos cos sin 51t t tt 也满足伏雷内公式 ;9.证明如果曲线的所有切线都经过一的定点,则此曲线是直线;证 方法一：取定点为坐标原点建坐标系,曲线的方程设为r ＝)(t r,则曲线在任意点的切线方程是)(')(t r t r λρ=-,由条件切线都过坐标原点,所以)(')(t r t rλ=,可见r ∥'r ,所以r 具有固定方向,故r ＝)(t r是直线;方法二：取定点为坐标原点建坐标系,曲线的方程设为r ＝)(t r,则曲线在任意点的切线方程是)(')(t r t rλρ=-,由条件切线都过坐标原点,所以)(')(t r t rλ=,于是'r ＝λ''r ,从而'r ×''r＝0 ,所以由曲率的计算公式知曲率k ＝０,所以曲线为直线;方法二：设定点为0r ,曲线的方程为r ＝()r s ,则曲线在任意点的切线方程是()()r s s ρλα-=,由条件切线都过定点0r ,所以0()()r r s s λα-=,两端求导得:()()s s αλαλκβ'-=+, 即(1)()0s λαλκβ'++= ,而(),()s s αβ无关,所以10λ'+=,可知0,()0s λκ≠∴=,因此曲线是直线;10. 证明如果曲线的所有密切平面都经过一的定点,则此曲线是平面曲线;证 方法一：取定点为坐标原点建坐标系,曲线的方程设为r ＝)(t r,则曲线在任意点的密切平面的方程是0))('')('())((=⨯⋅-t r t r t r ρ,由条件0))('')('()(=⨯⋅-t r t r t r,即r 'r ''r =0,所以r 平行于一固定平面,即r ＝)(t r是平面曲线;方法二：取定点为坐标原点建坐标系,曲线的方程设为r ＝)(s r,则曲线在任意点的密切平面方程是0))((=⋅-γρ s r ,由条件0)(=⋅γs r ,两边微分并用伏雷内公式得τ-0)(=⋅β s r ;若0)(=⋅β s r ,又由0)(=⋅γ s r 可知)(s r ∥)(s r •= α,所以r ＝)(s r平行于固定方向,这时r ＝)(s r表示直线,结论成立;否则0=τ,从而知曲线是平面曲线;方法三：取定点为坐标原点建坐标系,曲线的方程设为r ＝)(t r,则曲线在任意点的密切平面方程是0))('')('())((=⨯⋅-t r t r t r ρ,由条件0))('')('()(=⨯⋅-t r t r t r,即r 'r ''r =0,所以r ,'r ,''r 共面,若r ∥'r ,则r ＝)(t r是直线,否则可设''',''''''r r r r r r λμλμ=+∴=+,所以','','''r r r 共面,所以0=τ,从而知曲线是平面曲线;11. 证明如果一条曲线的所有法平面包含常向量e,那么曲线是直线或平面曲线;证 方法一：根据已知0=⋅e α,若α是常向量,则k=||•α =0 ,这时曲线是直线;否则在0=⋅e α两边微分得•α ·e =０,即 k β ·e =０,所以β ·e =０,又因0=⋅e α,所以γ ∥e ,而γ 为单位向量,所以可知γ 为常向量,于是0||||==•γτ,即0=τ,此曲线为平面曲线;方法二：曲线的方程设为r ＝)(t r ,由条件'r ·e ＝０,两边微分得''r ·e ＝０,'''r ·e＝０,所以'r , ''r ,'''r共面,所以'r ''r '''r ＝０;由挠率的计算公式可知0=τ,故曲线为平面曲线;当'r ×''r＝0 时是直线;方法三：曲线的方程设为r ＝)(t r,由条件'r ·e ＝０,两边积分得p 是常数;因r e p ⋅=是平面的方程,说明曲线r ＝)(t r在平面上,即曲线是平面曲线,当'r 有固定方向时为直线;12．证明曲率为常数的空间曲线的曲率中心的轨迹仍是曲率为常数的曲线;证明 设曲线C ：r ＝)(s r的曲率k 为常数,其曲率中心的轨迹C 的方程为：)(1)(s ks r βρ+= ,β 为曲线C 的主法向量,对于曲线C 两边微分得γτγτααρ kk k s =+-+=)(1)(' ,α ,γ ,τ分别为曲线C 的单位切向量,副法向量和挠率,βτγτρ k k 2''-=•,k |||'|τρ= ,23'''k τρρ=⨯ α ,曲线C 的曲率为k k k k ==⨯=-33233|||||'||'''|ττρρρ为常数;13.证明曲线x=1+3t+22t ,y=2-2t+52t ,z=1-2t 为平面曲线,并求出它所在的平面方程 ;证 'r ={3+4t, -２+10t,-2t}, ''r ={4,10,-２}, '''r＝｛０,0,0｝曲线的挠率是0)'''()''','','(2=⨯=r r r r r τ,所以曲线为平面曲线;曲线所在平面是曲线在任一点的密切平面;对于ｔ=０,r =｛１,２,１｝,'r ={3, -２,０}, ''r ={4,10,-２}, '''r＝｛０,0,0｝;所以曲线的密切平面,即曲线所在平面是02104023121=-----z y x ,即2x+3y+19z –27＝０．14．设在两条曲线Γ、Γ的点之间建立了一一对应关系,使它们在对应点的切线平行,证明它们在对应点的主法线以及副法线也互相平行;证 设曲线Γ：r =)(s r与Γ：)(s r r =点s 与s 一一对应,且对应点的切线平行,则)(s α=)(s α±, 两端对s 求微商得ds s d αα ±=, 即dss d s k s k )()(ββ ±= ,这里k ≠0,若k=||α =0,则β 无定义,所以β ∥β ,即主法线平行,那么两曲线的副法线也平行;15．设在两条曲线Γ、Γ的点之间建立了一一对应关系,使它们在对应点的主法线平行,证明它们在对应点的切线作固定角;证 设α ,α分别为曲线Γ、Γ的切向量,β ,β 分别为曲线Γ、Γ的主法向量,则由已知)()(s s ββ ±=．．．．．① ,而ds s d ds d αααααα ⋅+⋅=⋅)(＝ dss d s k k )(βααβ ⋅+⋅ 将①式代入 0)(=⋅±⋅dss d k βααβ ;所以α ·α＝常数,故量曲线的切线作固定角;16.若曲线Γ的主法线是曲线Γ的副法线, Γ的 曲率、挠率分别为τκ,;求证k=0λ2κ+2τ ,其中0λ为常数;证 设Γ的向量表示为r =)(s r,则Γ可表示为ρ =)(s r +)(s λ)(s β , Γ的切向量'ρ =α+λ β +λ－k α +τγ 与β 垂直,即'ρ ·β ＝λ ＝０,所以λ为常数,设为0λ,则'ρ ＝１－0λk α +0λτγ ;再求微商有''ρ ＝－0λk α＋１－0λkk β ＋0λτ γ －0λ2τβ ,''ρ ·β ＝１－0λkk －0λ2τ＝０,所以有k=0λ2κ+2τ;17．曲线r ={at-sint,a1-cost,4acos2t}在那点的曲率半径最大;解 'r= a{1-cost,sint,-2sin2t } , ''r = a{sint,cost,-cos 2t}, |2sin |22|'|tr = ,'r ×''r =}1,2cos ,2{sin 2sin 2}2cos 4,2cos 2sin 2,2sin 2{22232tt t a t a t t t a -=--,|'r ×''r |=22sin 222t a , |2sin|81|||'''|3ta r r r k =⨯=,|2sin |8t a R = ,所以在t=2k+1π,k 为整数处曲率半径最大;18． 已知曲线)(:)(3s r r C C =∈上一点)(0s r 的邻近一点)(0s s r ∆+ ,求)(0s s r ∆+点到)(0s r 点的密切平面、法平面、从切平面的距离设点)(0s r 的曲率、挠率分别为00,τκ;解)(0s s r ∆+－)(0s r ＝30200])([!31)(21)(s s r s s r s s r ∆++∆+∆ε ＝300021s s ∆+∆βκα ＋300000020)(61s k k ∆+++-εγτκβα ,设030201γεβεαεε ++=,其中0lim 0=→∆ε s ;则)(0s s r ∆+ －)(0s r＝0330003202003120])(61[])(6121[])(61[γετκβεκκαεκ s s s s s ∆++∆++∆+∆+-+∆ 上式中的三个系数的绝对值分别是点)(0s s r ∆+ 到)(0s r的法平面、从切平面、密切平面的距离;§5 一般螺线5. 证明如果所有密切平面垂直于固定直线,那么它是平面直线.证法一: 当曲线的密切平面垂直于某固定直线时,曲线的副法向量γ是常向量.即γ=0;曲线的挠率的绝对值等于|γ|为零,所以曲线为平面曲线; 证法二：设n 是固定直线一向量,则'r ·n =0 ,积分得r ·n=p ,说明曲线在以n 为法向量的一个平面上,因而为平面直线;证法三：设n 是固定直线一向量,则'r ·n =0 ,再微分得''r ·n =0 ,'''r ·n=0 ;所以'r 、''r 、'''r三向量共面,于是'r ''r '''r = 0 ,由挠率的计算公式知τ=0,因此曲线为平面曲线;7．如果两曲线在对应点有公共的副法线,则它们是平面曲线;证 设一曲线为Γ：r ＝)(s r,则另一曲线Γ的表达式为：+=)(s r ρ)(s λ)(s γ ,)(s γ 为曲线Γ在点s 的主法向量,也应为Γ在对应点的副法线的方向向量;'ρ ＝α＋λ γ －λτβ 与γ 正交,即'ρ ·γ ＝０,于是λ ＝０,λ为常数;'ρ ＝α －λτβ ,''ρ ＝k β －λτ β －λτ－k α＋τγ 也与γ 正交,即''ρ ·γ ＝-λ2τ=0,而λ≠０,所以有τ＝０,曲线Γ为平面曲线;同理曲线Γ为平面曲线;8. 如果曲线Γ：r ＝)(s r为一般螺线, α、β 为Γ的切向量和主法向量,R 为Γ的曲率半径;证明Γ：ρ=R α－⎰ds β 也是一般螺线;证 因为Γ为一般螺线, 所以存在一非零常向量e 使α与e成固定角,对于曲线Γ,其切向量'ρ=αββκα R R R =-+与α共线,因此也与非零常向量e 成固定角, 所以Γ也为一般螺线;9．证明曲线r ＝)(s r 为一般螺线的充要条件为0),,(....=r r r证 βκ =r ,γτκτκβκτκκακκγκτβκακ )2()(3,23....2++-+-+-=++-=r r 25333....)(3)2(),,(κτκτκκτκτκκτκκτκτκ -=-=-+=k r r r ＝)(5κτκ,其中k ≠0. 曲线r ＝)(s r 为一般螺线的充要条件为κτ为常数,即•)(κτ=0,也就是0),,(....=r r r ;方法二： 0),,(....=r r r ,即0),,(=ααα;曲线r ＝)(s r 为一般螺线,则存在常向量e ,使α·e =常数,所以,0,0,0=⋅=⋅=⋅e e e ααα所以ααα ,,共面,从而ααα ,,=0;反之,若ααα ,,=0,则α 平行于固定平面,设固定平面的法矢为e ,则有0=⋅e α,从而α·e = p 常数,所以r ＝)(s r 为一般螺线;方法三：曲线r ＝)(s r 为一般螺线⇔存在常向量e 使e β⊥,即0e ββ⋅=⇔平行于固定平面以e 为法向量的平面r ⇔平行于一固定平面(,,)0r r r ⇔= ;方法四：""⇒设r ＝)(s r 为一般螺线,存在常向量e 使e α⋅=常数,即r e ⋅=常数,连续三次求微商得0,0r e r e ⋅=⋅=,0r e ⋅= ,所以0),,(....=r r r ;""⇐因为0),,(....=r r r ,所以r 平行于固定平面,设固定平面的法矢为n 常向量,则r n ⊥,而,r n ββ∴⊥,所以曲线为一般螺线;10. 证明一条曲线的所有切线不可能同时都是另一条曲线的切线;证 设曲线Γ与Γ在对应点有公共的切线,且Γ的表达式为：r ＝)(s r ,则Γ：+=)(s r ρ)(s λ)(s α ,λ≠０,其切向量为'ρ＝α＋λ α＋λk β 应与α平行,所以k ＝０,从而曲线Γ为直线;同理曲线Γ为直线,而且是与Γ重合的直线;所以作为非直线的两条不同的曲线不可能有公共的切线;11．设在两条曲线Γ、Γ的点之间建立了一一对应关系,使它们在对应点的切线平行,证明它们在对应点的主法线以及副法线也互相平行,且它们的挠率和曲率都成比例,因此如果Γ为一般螺线, 则Γ也为一般螺线;证 设曲线Γ：r =)(s r 与Γ：)(s r r =点建立了一一对应,使它们对应点的切线平行,则适当选择参数可使)(s α =)(s α , 两端对s 求微商得ds s d αα =, 即ds s d s k s k )()(ββ = ,这里0 ds s d ,所以有β =β ,即主法线平行,从而)(s γ =)(s γ ,即两曲线的副法线也平行;且,ds s d κκ= 或ds s d =κκ;)(s γ =)(s γ 两边对s 求微商得dss d s s )()(βτβτ -=-,于是 ,ds s d ττ=或ds s d =ττ,所以,ττκκ= 或τκτκ=;。