2020届高考数学三轮小专题《8.3 基本不等式及其应用》典例导引+课后精练(无答案)
- 格式:docx
- 大小:200.03 KB
- 文档页数:4

专题08 基本不等式及其应用(平均值不等式及其应用,三角不等式)知识梳理一、基本不等式:1.若,a b R ∈,222a b ab +≥,当且仅当a =b 时取等号2.(1)“积定和最小”:ab b a 2≥+⇔如果积ab 是定值P ,那么当a b =时,和a b +有最小值(2)“和定积最大”:22⎪⎭⎫ ⎝⎛+≤b a ab ⇔如果和a b +是定值S ,那么当a b =时,积ab 有最大值214S 。
3.若,a b R +∈2a b+≥ 加权平均》算术平均》几何平均二、平均值不等式:若a 、b 为正数,则2a b+≥a b =时取等号变式:222()22a b a b ab ++≥≥推广:123,,,,n a a a a 是n 个正数,则12na a a n+++称为这n 个正数的算术平均数,称为这n个正数的几何平均数,它们的关系是:12n a a a n ++⋅⋅⋅+≥12n a a a ===时等号成立。
三、三角形不等式如果,a b 是实数,则a b a b a b -±+≤≤ 注:当b a ,为复数或向量时结论也成立. 推论1:1212n n a a a a a a ++++++≤推论2:如果a b c 、、是实数,那么a c a b b c --+-≤,当且仅当()()0a b b c --≥时,等号成立.例题解析一、简单基本不等式问题【例1】条件“0>a 且0>b ”是结论“ab ba ≥+2”成立的 条件。
【难度】★【答案】充分非必要条件 【例2】已知正数y x ,满足12=+y x ,求yx 11+的最小值。
判断下述解法正确与否,若不正确,请给出正确的解法,若正确,则说明理由。
y x xyxy y x xy y x y x 112422221,2110,0+∴≥∴≥+=≥+∴>> 的最小值为24【难度】★【答案】不正确,忽略了前两个小不等式中的取等条件, 当时,即,取得最小值。

专题08 导数与不等式、函数零点相结合 文考纲解读明方向2020年高考全景展示1.【2020年浙江卷】已知函数f (x )= −ln x .(Ⅰ)若f (x )在x =x 1,x 2(x 1≠x 2)处导数相等,证明:f (x 1)+f (x 2)>8−8ln2;(Ⅱ)若a ≤3−4ln2,证明:对于任意k >0,直线y =kx +a 与曲线y =f (x )有唯一公共点. 【答案】(Ⅰ)见解析 (Ⅱ)见解析【解析】分析: (Ⅰ)先求导数,根据条件解得x 1,x 2关系,再化简f (x 1)+f (x 2)为,利用基本不等式求得取值范围,最后根据函数单调性证明不等式,(Ⅱ)一方面利用零点存在定理证明函数有零点,另一方面,利用导数证明函数在上单调递减,即至多一个零点.两者综合即得结论.所以g (x )在[256,+∞)上单调递增,故,即.由(Ⅰ)可知g (x )≥g (16),又a ≤3–4ln2,故–g (x )–1+a ≤–g (16)–1+a =–3+4ln2+a ≤0,所以h′(x)≤0,即函数h(x)在(0,+∞)上单调递减,因此方程f(x)–kx–a=0至多1个实根.综上,当a≤3–4ln2时,对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.点睛:利用导数证明不等式常见类型及解题策略:(1) 构造差函数.根据差函数导函数符号,确定差函数单调性,利用单调性得不等量关系,进而证明不等式.(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.2.【2020年全国卷Ⅲ文】已知函数.(1)求曲线在点处的切线方程;(2)证明:当时,.【答案】(1)切线方程是(2)证明见解析【解析】分析:(1)求导,由导数的几何意义求出切线方程。
(2)当时,,令,只需证明即可。
详解:(1),.因此曲线在点处的切线方程是.(2)当时,.令,则.当时,,单调递减;当时,,单调递增;所以.因此.点睛:本题考查函数与导数的综合应用,由导数的几何意义可求出切线方程,第二问当时,,令,将问题转化为证明很关键,本题难度较大。

不等式综合 【考点导读】 能利用不等式性质、定理、不等式解法及证明解决有关数学问题和实际问题,如最值问题、恒成立问题、最优化问题等. 【基础练习】 1.若函数,则与的大小关系是 2.函数在区间上恒为正,则的取值范围是0<a<2 3.当点在直线上移动时,的最小值是7 4.已知f(x)、g(x)都是奇函数,f(x)>0的解集是(a2,b),g(x)>0的解集是(,),则f(x)·g(x)>0的解集是m≤4的m,不等式x2+mx>4x+m-3x的取值范围是x>3或x<1 【范例导析】 例1、已知集合,函数的定义域为Q (1)若,求实数a的取值范围。
(2)若方程在内有解,求实数a的取值范围。
分析:问题(1)可转化为在内有有解;从而和问题(2)是同一类型的问题,既可以直接构造函数角度分析,亦可以采用分离参数. 解:(1)若,在内有有解 令 当时, 所以a>-4,所以a的取值范围是 (2)方程在内有解 则在内有解 当时, 所以时,在内有解 点拨:本题用的是参数分离的思想 例2.已知f(x)是定义在[—1,1]上的奇函数,且f (1)=1,若m、n∈[—1,1],m+n≠0 (1)判断f (x)在[—1,1]上的单调性,并证明你的结论; (2)解不等式:; (3)若f (x)≤对所有x∈[—1,1],∈[—1,1]恒成立,求实数t的取值范围. 分析:可利用定义法判断单调性,再利用单调性解决问题(2),问题(3)只要f (x)max≤ 解:(1)任取—1≤x1<x2≤1,则 f (x1)—f (x2)=f (x1)+f (-x2)=∵—1≤x1<x2≤1,∴x1+(-x2)≠0, 由已知>0,又x1-x2<0, ∴f (x1)—f (x2)<0,即f (x)在[—1,1]上为增函数. (2)∵f (x)在[—1,1]上为增函数,故有 (3)由(1)可知:f(x)在[—1,1]上是增函数,且f (1)=1,故对x∈[—l,1], 恒有f(x)≤1. 所以要使f(x)≤,对所有x∈[—1,1], ∈[—1,1]恒成立, 即要≥1成立,故≥0成立. 记g()=对 ∈[—1,1],g()≥0恒成立,只需g()在[—1,1]上的最小值 大于等于零. 故 解得:t≤—2或t=0. 点拨:一般地,若与若分别存在最大值和最小值,则恒成立等价于. 例3.甲、乙两地相距,汽车从甲地匀速行驶到乙地,速度不超过,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度的平方成正比,且比例系数为;固定部分为元. (1)把全程运输成本元表示为速度的函数,并指出这个函数的定义域; (2)为了使全程运输成本最小,汽车应以多大速度行驶? 分析:需由实际问题构造函数模型,转化为函数问题求解 解:(1)依题意知汽车从甲地匀速行驶到乙地所用的时间为,全程运输成本为 . 故所求函数为,定义域为. (2)由于都为正数, 故有, 即. 当且仅当,即时上式中等号成立. 若时,则时,全程运输成本最小; 当,易证,函数单调递减,即时,. 综上可知,为使全程运输成本最小, 在时,行驶速度应为; 在时,行驶速度应为. 点拨:本题主要考查建立函数关系式、不等式性质(公式)的应用.也是综合应用数学知识、思想和方法解决实际问题的一道优秀试题. 反馈练习: 1.设,函数,则使的的取值范围是 2.一个直角三角形的周长为2P,其斜边长的最小值 3.首项为-24的等差数列,从第10项起开始为正数,则公差d的取值范围是 4.如果函数的单调递增区间是(-∞,a],那么实数a的取值范围是____ a<-1____ 5.若关于的不等式对任意恒成立,则实数的取值范围为 6.设实数m,n,x,y满足的最大值 7.已知关于x的方程sin2x+2cosx+a=0有解,则a的取值范围是[-2,2]0≤p≤4的所有实数p,使不等式都成立的x的取值范围 9..三个同学对问题“关于的不等式+25+|-5|≥在[1,12]上恒成立,求实数的取值范围”提出各自的解题思路. 甲说:“只须不等式左边的最小值不小于右边的最大值”. 乙说:“把不等式变形为左边含变量的函数,右边仅含常数,求函数的最值”. 丙说:“把不等式两边看成关于的函数,作出函数图像”. 参考上述解题思路,你认为他们所讨论的问题的正确结论,即的取值范围是 a≤10 10.设曲线在点处的切线斜率为,且,对一切实数,不等式恒成立() , , 又, 即 11.已知二次函数f (x)=,设方程f (x)=x的两个实根为x1和x2. (1)如果x1<2<x2<4,且函数f (x)的对称轴为x=x0,求证:x0>—1; (2)如果x10,即 ∴ (2)由g(x)=. ①若0<x12,∴g(2)=4a+2b—1<0, 又,代入上式得 ②若-2<x1<0,则x2=-2+x1<-2,∴g(-2)<0,即4a-2b+3<0,同理可求得. 故当0<x1<2时, ;当-2<x1<0时,. 12.已知A、B两地相距200km,一只船从A地逆水到B地,水速为8km/h,船在静水中的速度为v km/h(80),则 当v=12时,y1=720 得k=5 设全程燃料费为y,依题意有 当,即v=16时取等号 8<v 所以当时,v=16时全程燃料费最省 当时,令 任取 则 即在上为减函数,当v=v0时,y取最小值 综合得:当时,v=16km/h,全程燃料费最省,32000为元,当时,当v=v0时,全程燃料费最省,为元。

(江苏专用)2020版高考数学三轮复习小题专题练(一)集合、常用逻辑用语、不等式、函数与导数文苏教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((江苏专用)2020版高考数学三轮复习小题专题练(一)集合、常用逻辑用语、不等式、函数与导数文苏教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(江苏专用)2020版高考数学三轮复习小题专题练(一)集合、常用逻辑用语、不等式、函数与导数文苏教版的全部内容。
小题专题练(一)集合、常用逻辑用语、不等式、函数与导数(建议用时:50分钟)1.已知集合A={x|(x+1)(x-2)〉0},B={x|-1≤x-1≤1},则A∩(∁R B)=________.2.(2019·苏州模拟)函数f(x)=错误!的定义域为________.3.已知a>0,b>0,且满足3a+b=a2+ab,则2a+b的最小值为________.4.(2019·南通调研)函数f(x)=lg x2的单调递减区间是________.5.若f(x)=ln(e3x+1)+ax是偶函数,则a=________.6.(2019·泰州期末)曲线y=2ln x在点(e,2)处的切线(e是自然对数的底数)与y轴交点的坐标为________.7.已知命题p:方程x2-2ax-1=0有两个实数根;命题q:函数f(x)=x+错误!的最小值为4.给出下列命题:①p∧q;②p∨q;③p∧(綈q);④(綈p)∨(綈q).其中是真命题的为________.(把所有正确命题的序号都填上)8.已知x,y满足约束条件错误!则z=2x+y的最大值为________.9.(2019·苏北四市联考)点P是曲线y=x2-ln x上任意一点,则P到直线y=x-2的距离的最小值是________.10.若关于x的不等式(2ax-1)ln x≥0对任意的x>0恒成立,则实数a的取值范围是________.11.设二次函数f(x)=ax2+bx+c(a,b,c为常数)的导函数为f′(x).对任意x∈R,不等式f(x)≥f′(x)恒成立,则错误!的最大值为________.12.已知定义在R上的偶函数f(x)满足f(x-4)=f(x),且在区间[0,2]上f(x)=x,若关于x的方程f(x)=log a x有三个不同的根,则a的取值范围为________.13.(2019·常州模拟)已知函数f(x)=x2e x,若f(x)在[t,t+1]上不单调,则实数t的取值范围是________.14.a为实数,函数f(x)=|x2-ax|在区间[0,1]上的最大值记为g(a).当a=________时,g(a)的值最小.小题专题练(一)1.解析:A={x|(x+1)(x-2)>0}={x|x〈-1或x〉2}.因为B={x|-1≤x-1≤1},所以B={x|0≤x≤2},所以∁R B={x|x〈0或x>2},所以A∩(∁R B)={x|x<-1或x〉2}.答案:{x|x〈-1或x>2}2.解析:若函数f(x)有意义,则错误!所以log2x>1,所以x>2.答案:(2,+∞)3.解析:因为a>0,b>0,且满足3a+b=a2+ab,所以b=错误!>0,解得1<a<3,则2a+b=2a+错误!=a-1+错误!+3≥2错误!+3=2错误!+3,当且仅当a=1+错误!,b=1时取等号.答案:3+2错误!4.解析:函数f(x)=lg x2的单调递减区间需满足x2〉0且y=x2单调递减,故x∈(-∞,0).答案:(-∞,0)5.解析:由偶函数的定义可得f(-x)=f(x),即ln (e-3x+1)-ax=ln(e3x+1)+ax,所以2ax=-ln e3x=-3x,所以a=-错误!.答案:-错误!6.解析:由曲线y=2ln x得y′=错误!,所以k=错误!,所以点(e,2)处的切线方程为y-2=错误!(x-e),令x=0得y=0,所以曲线y=2ln x在点(e,2)处的切线与y轴交点的坐标为(0,0).答案:(0,0)7.解析:因为Δ=(-2a)2-4×(-1)=4a2+4〉0,所以方程x2-2ax-1=0有两个实数根,所以命题p是真命题;当x〈0时,函数f(x)=x+错误!的取值为负值,所以命题q 为假命题,所以p∨q,p∧(綈q),(綈p)∨(綈q)是真命题.答案:②③④8.解析:x,y满足的平面区域如图阴影部分所示,根据阴影部分可得,当直线z=2x+y与圆相切于第一象限时,z取最大值,此时错误!=2,所以z的最大值为2错误!.答案:2错误!9.解析:y′=2x-1x,由y′=1,得2x-错误!=1,x=1.切点为(1,1),它到直线y=x-2的距离为错误!.答案:错误!10.解析:若x=1,则不等式成立,若x>1,则ln x>0,则不等式等价为2ax-1≥0对x>1恒成立,即2ax≥1,即a≥错误!,因为错误!<错误!,所以a≥错误!,若0<x<1,则ln x<0,则不等式等价为(2ax-1)≤0对0<x<1恒成立,即2ax≤1,即a≤12x,因为错误!>错误!,所以a≤错误!,综上a=错误!。
专题08 导数与不等式、函数零点相结合2018年高考全景展示1.【2018年全国卷Ⅲ理】已知函数. (1)若,证明:当时,;当时,;(2)若是的极大值点,求.【答案】(1)见解析(2)当时,;当时,.故当时,,且仅当时,,从而,且仅当时,.所以在单调递增.又,故当时,;当时,. (2)(i )若,由(1)知,当时,,这与是的极大值点矛盾.(ii )若,设函数.由于当时,,故与符号相同.又,故是的极大值点当且仅当是的极大值点..如果,则当,且时,,故不是的极大值点.如果,则存在根,故当,且时,,所以不是的极大值点.如果,则.则当时,;当时,.所以是的极大值点,从而是的极大值点,综上,.点睛:本题考查函数与导数的综合应用,利用函数的单调性求出最值证明不等式,第二问分类讨论和,当时构造函数时关键,讨论函数的性质,本题难度较大。
2.【2018年理数全国卷II】已知函数.(1)若,证明:当时,;(2)若在只有一个零点,求.【答案】(1)见解析(2)【解析】分析:(1)先构造函数,再求导函数,根据导函数不大于零得函数单调递减,最后根据单调性证得不等式,(2)研究零点,等价研究的零点,先求导数:,这里产生两个讨论点,一个是a与零,一个是x与2,当时,,没有零点;当时,先减后增,从而确定只有一个零点的必要条件,再利用零点存在定理确定条件的充分性,即得a的值.(2)设函数.在只有一个零点当且仅当在只有一个零点.(i)当时,,没有零点;(ii)当时,.当时,;当时,.所以在单调递减,在单调递增.故是在的最小值.①若,即,在没有零点;②若,即,在只有一个零点;③若,即,由于,所以在有一个零点,由(1)知,当时,,所以.故在有一个零点,因此在有两个零点.综上,在只有一个零点时,.点睛:利用函数零点的情况求参数值或取值范围的方法(1)利用零点存在的判定定理构建不等式求解.(2)分离参数后转化为函数的值域(最值)问题求解.(3)转化为两熟悉的函数图象的上、下关系问题,从而构建不等式求解.3.【2018年江苏卷】某农场有一块农田,如图所示,它的边界由圆O的一段圆弧(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为,要求均在线段上,均在圆弧上.设OC与MN所成的角为.(1)用分别表示矩形和的面积,并确定的取值范围;(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为.求当为何值时,能使甲、乙两种蔬菜的年总产值最大.【答案】(1)矩形ABCD的面积为800(4sinθcosθ+cosθ)平方米,△CDP的面积为1600(cosθ–sinθcosθ),sinθ的取值范围是[,1).(2)当θ=时,能使甲、乙两种蔬菜的年总产值最大【解析】分析:(1)先根据条件求矩形长与宽,三角形的底与高,再根据矩形面积公式以及三角形面积公式得结果,最后根据实际意义确定的取值范围;(2)根据条件列函数关系式,利用导数求极值点,再根据单调性确定函数最值取法.详解:解:(1)连结PO并延长交MN于H,则PH⊥MN,所以OH=10.过O作OE⊥BC于E,则OE∥MN,所以∠COE=θ,故OE=40cosθ,EC=40sinθ,则矩形ABCD的面积为2×40cosθ(40sinθ+10)=800(4sinθcosθ+cosθ),△CDP的面积为×2×40cosθ(40–40sinθ)=1600(cosθ–sinθcosθ).过N作GN⊥MN,分别交圆弧和OE的延长线于G和K,则GK=KN=10.令∠GOK=θ0,则sinθ0=,θ0∈(0,).当θ∈[θ0,)时,才能作出满足条件的矩形ABCD,所以sinθ的取值范围是[,1).答:矩形ABCD的面积为800(4sinθcosθ+cosθ)平方米,△CDP的面积为1600(cos θ–sin θcos θ),sin θ的取值范围是[,1).令,得θ=,当θ∈(θ0,)时,,所以f (θ)为增函数;当θ∈(,)时,,所以f (θ)为减函数,因此,当θ=时,f (θ)取到最大值.答:当θ=时,能使甲、乙两种蔬菜的年总产值最大.点睛:解决实际应用题的步骤一般有两步:一是将实际问题转化为数学问题;二是利用数学内部的知识解决问题.2017年高考全景展示1.【2017课标3,理11】已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .1【答案】C 【解析】试题分析:函数的零点满足()2112x x x x a e e --+-=-+, 设()11x x g x ee--+=+,则()()211111111x x x x x x e g x eeee e ---+----'=-=-=,当()0g x '=时,1x =,当1x <时,()0g x '<,函数()g x 单调递减, 当1x >时,()0g x '>,函数()g x 单调递增, 当1x =时,函数取得最小值()12g =,设()22h x x x =- ,当1x =时,函数取得最小值1- ,若0a ->,函数()h x 与函数()ag x 没有交点,当0a -<时,()()11ag h -=时,此时函数()h x 和()ag x 有一个交点, 即21a -⨯=-,解得12a =.故选C. 【考点】 函数的零点;导函数研究函数的单调性,分类讨论的数学思想【名师点睛】函数零点的应用主要表现在利用零点求参数范围,若方程可解,通过解方程即可得出参数的范围,若方程不易解或不可解,则将问题转化为构造两个函数,利用两个函数图象的关系求解,这样会使得问题变得直观、简单,这也体现了数形结合思想的应用. 2.【2017课标1,理21】已知函数2()(2)xx f x ae a e x =+--.(1)讨论()f x 的单调性;(2)若()f x 有两个零点,求a 的取值范围. 【解析】试题分析:(1)讨论()f x 单调性,首先进行求导,发现式子特点后要及时进行因式分解,在对a 按0a ≤,0a >进行讨论,写出单调区间;(2)根据第(1)题,若0a ≤,()f x 至多有一个零点.若0a >,当ln x a =-时,()f x 取得最小值,求出最小值1(ln )1ln f a a a-=-+,根据1a =,(1,)a ∈+∞,(0,1)a ∈进行讨论,可知当(0,1)a ∈有2个零点,设正整数0n 满足03ln(1)n a>-,则00000000()e (e 2)e 20n n n n f n a a n n n =+-->->->.由于3ln(1)ln a a->-,因此()f x 在(ln ,)a -+∞有一个零点.所以a 的取值范围为(0,1).(2)(ⅰ)若0a ≤,由(1)知,()f x 至多有一个零点.(ⅱ)若0a >,由(1)知,当ln x a =-时,()f x 取得最小值,最小值为1(ln )1ln f a a a-=-+. ①当1a =时,由于(ln )0f a -=,故()f x 只有一个零点; ②当(1,)a ∈+∞时,由于11ln 0a a-+>,即(ln )0f a ->,故()f x 没有零点;③当(0,1)a ∈时,11ln 0a a-+<,即(ln )0f a -<. 又422(2)e(2)e 22e 20f a a ----=+-+>-+>,故()f x 在(,ln )a -∞-有一个零点.设正整数0n 满足03ln(1)n a>-,则00000000()e (e 2)e 20n n n nf n a a n n n =+-->->->. 由于3ln(1)ln a a->-,因此()f x 在(ln ,)a -+∞有一个零点. 综上,a 的取值范围为(0,1).【考点】含参函数的单调性,利用函数零点求参数取值范围.【名师点睛】研究函数零点问题常常与研究对应方程的实根问题相互转化.已知函数()f x 有2个零点求参数取值范围,第一种方法是分离参数,构造不含参数的函数,研究其单调性、极值、最值,判断y a =与其交点的个数,从而求出a 的范围;第二种方法是直接对含参函数进行研究,研究其单调性、极值、最值,注意点是若()f x 有2个零点,且函数先减后增,则只需其最小值小于0,且后面还需验证有最小值两边存在大于0的点. 3.【2017课标II ,理】已知函数()2ln f x ax ax x x =--,且()0f x ≥。
2020届高考理科数学第三轮复习精编模拟八参考公式:如果事件A B ,互斥,那么球的表面积公式 ()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么其中R 表示球的半径 ()()()P A B P A P B =g g球的体积公式如果事件A 在一次试验中发生的概率是p ,那么34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(012)k kn k n n P k C p p k n -=-=,,,…,第一部分 选择题(共50分)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的1、如果()732log log log 0x =⎡⎤⎣⎦,那么12x-等于( )()A 13()36B ()39C ()24D2 已知(){}()(){}222,,,1E x y y x F x y xy a =≥=+-≤,那么使E F F =I 成立的充要条件是( )()54A a ≥ ()54B a = ()1C a ≥ ()0D a >3、设f(x)是(-∞,∞)是的奇函数,f(x +2)=-f(x),当0≤x ≤1时,f(x)=x ,则f(7.5)等于( )(A ) 0.5 (B ) -0.5 (C ) 1.5 (D ) -1.5 4、若1>>b a ,P=b a lg lg ⋅,Q=()b a lg lg 21+,R=⎪⎭⎫ ⎝⎛+2lg b a ,则( )(A )RPQ (B )PQ R(C )Q PR (D )P RQ 5、函数y=sin(π3-2x)+sin2x 的最小正周期是( ) (A )π2(B ) π (C ) 2π (D ) 4π 6、在圆x 2+y 2=4上与直线4x +3y -12=0距离最小的点的坐标是( )(A )(85,65) (B )(85,-65) (C )(-85,65) (D )(-85,-65)7、不等式组⎪⎩⎪⎨⎧+->+->x x x x x 22330的解集是( )(A )(0,2) (B )(0,2.5) (C )(0,6) (D )(0,3) 8、在正n 棱锥中,相邻两侧面所成的二面角的取值范围是( )(A )(n n 2-π,π) (B )(n n 1-π,π) (C )(0,2π) (D )(n n 2-π,n n 1-π)9、定义在区间(-∞,+∞)的奇函数f(x)为增函数;偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合,设 a>b>0 ,给出下列不等式:① f(b)-f(-a)>g(a)-g(-b) ② f(b)-f(-a)<g(a)-g(-b) ③ f(a)-f(-b)>g(b)-g(-a) ④f(a)-f(-b)<g(b)-g(-a) 其中成立的是 ( )(A)①与④ (B)②与③ (C)①与③ (D )②与④ 10、若过定点)0,1(-M 且斜率为k 的直线与圆05422=-++y x x 在第一象限内的部分有交点,则k 的取值范围是( )A. 50<<k B. 05<<-k C. 130<<k D. 50<<k第二部分 非选择题(共100分)二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.11、如果不等式x a x x )1(42->-的解集为A ,且}20|{<<⊆x x A ,那么实数a 的取值范围是 。
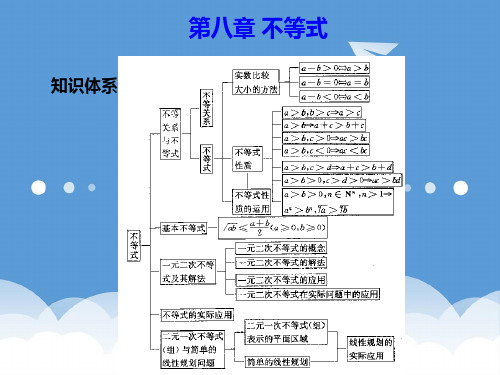
§8.3 基本不等式及其应用
【典题导引】
例1.(1)若,a b 均为非
负实数,且1a b +=,则
14
22a b a b
+
++的最小值为 ; (2)若正数,x y 满足22
49330x y xy ++=,则xy 的最大值是________;
(3)设正实数,,x y z 满足22340x xy y z -+-=,则当z
xy
取得最小值时,2x y z +-的
最大值为________.
例2.(1)在ABC ∆中,2
22tan tan tan 222
A B C
++的最小值是 . (2)(2016⋅江苏)在锐角ABC ∆中,若sin 2sin sin A B C =,则tan tan tan A B C 的最小
值是 . (3)(2017⋅南通二模)在ABC ∆中,已知2AB =,226AC BC -=,则tan C 的最大值
是 .
例3.已知数列{}n a 的前n 项和n S 满足()()1112
n n n n nS n S ++-+=
,*N n ∈,且11a =.
(1)求数列{}n a 的通项公式;
(2)令ln n n b a =,是否存在k (2,)k k *≥∈N ,使得k b ,1k b +,2k b +成等比数列.若
存在,求出所有符合条件的k 值;若不存在,请说明理由.
例4.如图,OA ,OB 是某港湾O 两侧的海岸线,120AOB ∠=o .随着经济的发展,为缓解
港湾O 的交通压力,拟在海岸线OA ,OB 上分别修建码头M N 、,开辟水上航线 MN .勘测发现:港湾O 周围3km 的区域内为浅水区,不适宜船只航行(即:为确保 航行安全,点O 与MN 的距离
d 须满足3d ≥).
(1)若5km OM =,3km ON =,问:船只沿水上航线MN 航行是否安全? (2)试确定码头M N 、的位置,使得船只安全航行,且航线MN 最短.
【课后巩固】
1.若正实数x y ,满足1x y +=,则4
y x y
+的最小值是 .
2.若对任意0x >,
2
31
x
a x x ≤++恒成立,则实数a 的取值范围为 .
3.已知0,0,8a b ab >>=,则当a 的值为 时,22log log (2)a b ⋅取得最大值.
4.某公司一年购买某种货物600吨,每次购买x 吨,运费为6万元/次,一年
的总存储费用为4x 万元,要使一年的总运费与总存储之和最小,则x 的值是 .
5.若实数,a b 满足12
a b
+=,则ab 的最小值为________.
6.函数22
14
sin cos y x x
=+的最小值为________.
7.已知a b c ,,均为正数,且4()abc a b =+,则a b c ++的最小值为 .
8.在ABC △中,若sin 2sin cos 0A B C +=,则内角A 的最大值是 .
9.在平面直角坐标系xOy 中,设直线l 过点(1,2)P ,与x 、y 轴的正半轴分别交于(,0)A a ,
(0,)B b 两点.当AOB ∆的面积最小时,求直线l 的方程.
10.在平面直角坐标系xOy 中,已知点(0,1)A -, B 点在直线3y =-上,M 点满足//MB OA u u u r u u u r
,
MA AB MB BA ⋅=⋅u u u r u u u r u u u r u u u r
,M 点的轨迹为曲线C . (1)求C 的方程;
(2) P 为C 上的动点,l 为C 在P 点处的切线,求O 点到l 距离的最小值.
11.设正项等差数列{}n a 的前n 项和为n S ,其中12a a ≠.m k n a a a 、、是数列{}n a 中满足
n k k m a a a a -=-的任意项.
(1)求证:2m n k +=; (2)求证:2m n k S S S ⋅≤;
(3)求证:112m n k
S S S +≥.
12.如图,某机械厂要将长6 m ,宽2 m 的长方形铁皮ABCD 进行裁剪.已知点F 为AD 的
中点,点E 在边BC 上,裁剪时先将四边形CDFE 沿直线EF 翻折到MNFE 处(点C ,D 分别落在直线BC 下方点M ,N 处,FN 交边BC 于点P ),再沿直线PE 裁剪.
(1)当∠EFP =4
π
时,试判断四边形MNPE 的形状,并求其面积;
(2)若使裁剪得到的四边形MNPE 面积最大,请给出裁剪方案,并说明理由.
A B C D F E P
M N。