微波技术基础第二章课后答案---杨雪霞

w.
λ=
2π υ p 1 = = = β f f µε r ε 0
ww
sc oc 2－5 在长度为 d 的无耗线上测得 Z in (d ) 、 Z in (d ) 和接实际负载时的
Z in (d ) ，证明
sc oc 假定 Z in (d ) = j100Ω ， Z in (d ) = − j 25Ω ， Z in (d ) = 75∠30°Ω ,求 Z L 。
解： ΓL =
Z L − Z0 =0.2-0.4j=0.4472exp(-j1.11)=0.4472∠-63.44° ZL + Z0 VSWR = ρ =
1+ | ΓL | = 2.618 1− | ΓL |
幅分布图，并求其最大值和最小值。
解：
ΓL =
ww
w.
V ( d ) = VL+ e jβd (1+ | ΓL | e j ( Φ L − 2 βd ) ) 1 ∴V (3λ / 4) = VL+ e j 3π / 2 (1 + e j (π −3π ) ) = VL+ ( −4 / 3) = 600 3 + VL = −450V
w.
60 23 ln = 33.3Ω 2.25 10
网
2 × 10 −1 = 552.6Ω 2 × 10 −3
co m
解法二：在空气中υ p 所以 Z 0 =
= 3 ×108
1 1 = = 55.6Ω 8 υ p C1 3 × 10 × 60 × 10 −12
L1 =
Z0 55.6 = = 1.85 × 10 − 7 H 8 υ p 3 × 10
课
Ω；其输入端电压为 600V、试画出沿线电压、电流和阻抗的振

绪论什么是微波，微波有什么特点，微波有那些应用第一章1.传输线可用来传输电磁信号能量和构成各种微波元器件。

微波传输线是一种分布参数电路，线上的电压和电流是时间和空间位置的二元函数，它们沿线的变化规律可由传输线方程来描述。

传输线方程是传输线理论中的基本方程。

2.均匀无耗传输线方程为其解为其参量为，，，3.终端接的不同性质的负载，均匀无耗传输线有三种工作状态：(1) 当时，传输线工作于行波状态。

线上只有入射波存在，电压电流振幅不变，相位沿传播方向滞后；沿线的阻抗均等于特性阻抗；电磁能量全部被负载吸收。

(2) 当、和时，传输线工作于驻波状态。

线上入射波和反射波的振幅相等，驻波的波腹为入射波的两倍，波节为零；电压波腹点的阻抗为无限大，电压波节点的阻抗为零，沿线其余各点的阻抗均为纯电抗；没有电磁能量的传输，只有电磁能量的交换。

(3) 当 时，传输线工作于行驻波状态。

行驻波的波腹小于两倍入射波，波节不为零；电压波腹点的阻抗为最大的纯电阻，电压波节点的阻抗为最小的纯电阻；电磁能量一部分被负载吸收，另一部分被负载反射回去。

4. 表征传输线上参量有反射系数，驻波比 和输入阻抗间关系。

它们之间的关系为 0000tan '1(')(')tan '1(')l in l Z jZ z z Z z Z Z Z jZ z z ββ++Γ==+-Γ (2 )2 2 00()()()L L j j z j z j z L L L inin z e e e e Z z Z Z z Z ϕβϕββ'''----'Γ=Γ=Γ=Γ'-='+5． 阻抗圆图和导纳圆图是传输线进行阻抗计算和阻抗匹配的重要工具。

这部分主要是搞清楚圆图的组成原理，通过练习加深理解。

6.传输线阻抗匹配方法常用阻抗变换器和分支匹配器(单分支、双分支和三分支)第二章 常用微波传输线1. 本章主要讨论了矩形波导、圆波导、同轴线、其中矩形波导、圆波导和同轴线易采用场解法来分析其场分布和传输特性，特别是矩形导波系统TE10模的传输特性，包括截止波数，截止波长，波导波长、波阻抗、相速度等的分析与求解2. 各类传输线内传输的主模及其截止波长和单模传输条件3. 了解波导的激励与耦合方法第三章 微波集成传输线1. 了解微波集成传输线的特点及分类2. 掌握带状线、微带线中传输的模式及其场分布，了解它们的主要传输特性，了解微带线的色散特性及其衰减3. 掌握耦合微带线中传输的模式及其场分布，了解耦合微带线的分析方法；奇偶模分析方法，了解特性阻抗与耦合松紧的关系第四章微波网络1.微波系统包括均匀传输线和微波元件两大部分。

微波技术习题解答第1章练习题1.1 无耗传输线的特性阻抗Z0= 100()。

根据给出的已知数据，分别写出传输线上电压、电流的复数和瞬时形式的表达式：(1) R L= 100 ()，I L = e j0(mA)；(2) R L = 50()，V L = 100e j0(mV)；(3) V L = 200e j0 (mV)，I L = 0(mA)。

解：本题应用到下列公式：(1)(2)(3)(1) 根据已知条件，可得：V L = I L R L = 100(mV)，复数表达式为：瞬时表达式为：(2) 根据已知条件，可得：复数表达式为：瞬时表达式为：(3) 根据已知条件，可得：复数表达式为：瞬时表达式为：1.2 无耗传输线的特性阻抗Z0 = 100()，负载电流I L = j(A)，负载阻抗Z L = j100()。

试求：(1) 把传输线上的电压V(z)、电流I(z)写成入射波与反射波之和的形式；(2) 利用欧拉公式改写成纯驻波的形式。

解：根据已知条件，可得：V L = I L Z L = j(j100) = 100(V)，1.3 无耗传输线的特性阻抗Z0 = 75()，传输线上电压、电流分布表达式分别为试求：(1) 利用欧拉公式把电压、电流分布表达式改写成入射波与反射波之和的形式；(2) 计算负载电压V L、电流I L和阻抗Z L；(3) 把(1)的结果改写成瞬时值形式。

解：根据已知条件求负载电压和电流：电压入射波和反射波的复振幅为(1) 入射波与反射波之和形式的电压、电流分布表达式(2) 负载电压、电流和阻抗V L = V(0) = 150j75，I L = I(0) = 2 + j(3) 瞬时值形式的电压、电流分布表达式1.4 无耗传输线特性阻抗Z0 = 50()，已知在距离负载z1= p/8处的反射系数为 (z1)= j0.5。

试求(1) 传输线上任意观察点z处的反射系数(z)和等效阻抗Z(z)；(2) 利用负载反射系数 L计算负载阻抗Z L；(3) 通过等效阻抗Z(z)计算负载阻抗Z L。

微波技术基础课后习题
杜 英
2011.5.1
第二章 传输线理论
2-6 如图所示为一无耗传输线，已知工作频率
Z L 1 5 0 j 5 0
f 3G H z ， Z 0 1 0 0
Z 01
，
，欲使 A 处无反射，试求 l 和
。
答案：由输入阻抗定义知
Z in A Z 0 1 Z L jZ 0 1 tan l Z 0 1 jZ 位面沿轴向移动的速
vp
度，公式表示为
p

p
2
相波长 是等相位面在一个周期T内移动的距离，有

欲使电磁波传输信号，必须对波进行调制，调制后的波不再是单一频 率的波，而是一个含有多种频率的波。这些多种频率成分构成一个“波群”
2 又称为波的包络，其传播速度称为群速，用 v g 表示，即 v g v 1 c
c

、 ，随着频率的变化，传播长数 可能为虚数，也可能为实
0
数，还可以等于零。当
时，系统处于传输与截止状态之间的临界状态，此
时对应的波长为截止波长。
当 c 时，导波系统中传输该种波型。
当 c 时，导波系统中不能传输该种波型。
第三章 微波传输线
3-3 什么是相速、相波长和群速？对于TE波、TM波和TEM波，它们的相速 相波长和群速有何不同？ 答案： 相速
0.125
0.188
D
A
0 0.5
D
0.25
B
0.15
0.2
C
0.375
0.361
0.338
第三章 微波传输线
3-2 何谓波导截止波长 c ？工作波长 大于 c 或小于 c 时，电磁波的特性有

2-1 波导为什么不能传输TEM 波？答：一个波导系统若能传输TEM 波型，则在该系统中必须能够存在静电荷静电核或恒定电流，而在单导体所构成的空心金属波导馆内，不可能存在静电荷或恒定电流，因此也不可能传输TEM 波型。

2-2 什么叫波型？有哪几种波型？答：波型是指每一种能够单独地在规则波导中存在的电磁场的一种分布状态。

根据场的横向分量与纵向分量之间的关系式划分波型，主要有三种：TEM 波（0z E =，0z H =），TE 波(0z E =,0z H ≠),TM 波（0z E ≠，0z H =） 2-3 何谓TEM 波，TE 波和TM 波？其波阻抗和自由空间波阻抗有什么关系？答：0z E =，0z H =的为TEM 波；0z E =,0z H ≠为TE 波；0z E ≠，0z H =为TM 波。

TE 波阻抗：x TE y E wuZ H ηβ===>TM 波阻抗：x TM y E Z H w βηε=== 其中η为TEM 波在无限答煤质中的波阻抗。

2-4 试将关系式y z x H H jw E y z ε∂∂-=∂∂，推导为1()zx y H E j H jw yβε∂=+∂。

解：由y H 的场分量关系式0j zy H H eβ-=（0H 与z 无关）得：y y H j H zβ∂=-∂利用关系式y z x H H jw E y zε∂∂-=∂∂可推出： 11()()y z zx y H H H E j H jw y z jw yβεε∂∂∂=+=+∂∂∂ 2-5 波导的传输特性是指哪些参量？答：传输特性是指传输条件、传播常数、传播速度、波导波长、波形阻抗、传输功率以与损耗和衰减等。

2-6何为波导的截止波长c λ？当工作波长λ大于或小于c λ时，波导内的电磁波的特性有何不同？答： 当波沿Z 轴不能传播时呈截止状态，处于此状态时的波长叫截止波长，定义为2c ck πλ=； 当工作波长大于截止波长时，波数c k k <，此时电磁波不能在波导中传播； 当工作波长小于截止波长时，波数c k k >，此时电磁波能在波导内传播；2-7 矩形波导中的截止波长c λ和波导波长g λ，相速度p υ和群速度g υ有什么区别和联系？它们与哪些因素有关？ 答：波导波长为2g πλλβ==>，c λ为截止波长群速为g c υ=<，相速为p υ=，且2p g c υυ⋅=，与c ，工作波长λ，截止波长c λ有关。

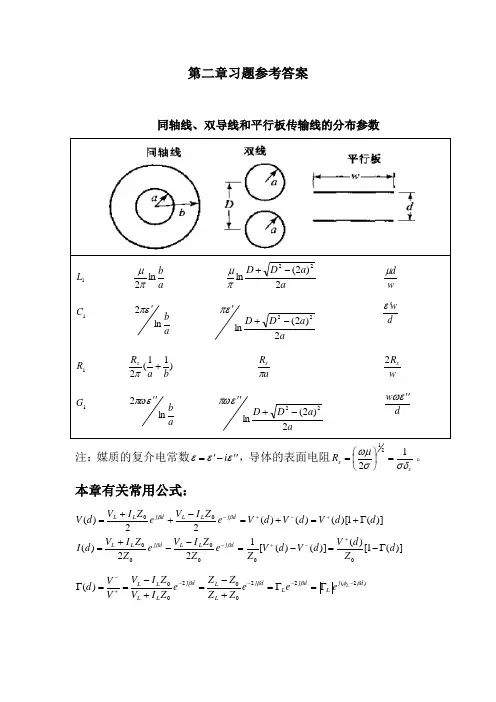
第二章习题参考答案同轴线、双导线和平行板传输线的分布参数注：媒质的复介电常数εεε''-'=i ，导体的表面电阻ss R σδσωμ1221=⎪⎭⎫⎝⎛=。

本章有关常用公式：)](1[)()]()([122)()](1)[()()(22)(00000000d Z d V d V d V Z e Z Z I V e Z Z I V d I d d V d V d V e Z I V e Z I V d V d j L L d j L L dj L L d j L L Γ-=-=--+=Γ+=+=-++=+-+-+-+-ββββ )2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==ΓL Lj L j L L L L L e e Z Z Z Z Z Z Z Z φφΓ=+-=+-=Γ0000dtg jZ Z dtg jZ Z Z d Z L L in ββ++=000)()(1)(1)()()(0d d Z d I d V d Z in Γ-Γ+==LL VV VSWR Γ-Γ+==11minmax2.1无耗或者低耗线的特性阻抗为110C L Z = 平行双导线的特性阻抗：aDa a D D a a D D Z r r rln 11202)2(ln 11202)2(ln 112222000εεεμεπ≈-+=-+=已知平行双导线的直径mm a 22=，间距cm D 10=，周围介质为空气（1=r ε），所以特性阻抗)(6.5521100ln 120ln11200Ω==≈a D Z rε 同轴线的特性阻抗：ab a b Z r rln 60ln 121000εεμεπ==已知同轴线外导体的内直径2mm b 23=，内导体的外直径2mm a 10=，中间填充空气(1=r ε)：特性阻抗)(50210223ln 60ln 600Ω===abZ r ε中间填充介质(25.2=r ε)：特性阻抗)(3.33210223ln 25.260ln 600Ω===a b Z r ε2.2对于无耗传输线线有相位常数μεωωβ===k C L 11，所以可求出相速度v k C L v p =====μεωβω1111，等于电磁波的传播速度。

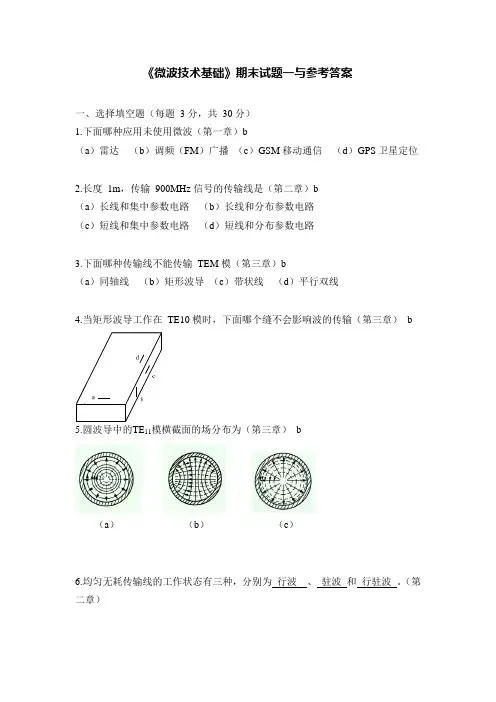
《微波技术基础》期末试题一与参考答案一、选择填空题（每题 3 分，共30 分）1.下面哪种应用未使用微波（第一章）b（a）雷达（b）调频（FM）广播（c）GSM 移动通信（d）GPS 卫星定位2.长度1m，传输900MHz 信号的传输线是（第二章）b（a）长线和集中参数电路（b）长线和分布参数电路（c）短线和集中参数电路（d）短线和分布参数电路3.下面哪种传输线不能传输TEM 模（第三章）b（a）同轴线（b）矩形波导（c）带状线（d）平行双线4.当矩形波导工作在TE10 模时，下面哪个缝不会影响波的传输（第三章）b5.圆波导中的TE11模横截面的场分布为（第三章）b（a）（b）（c）6.均匀无耗传输线的工作状态有三种，分别为行波、驻波和行驻波。

（第二章）Z L 0L 7.耦合微带线中奇模激励的对称面是 电 壁，偶模激励的对称面是 磁 壁。

（第三章）8.表征微波网络的主要工作参量有阻抗参量、 导纳 参量、 传输 参量、散射参量和 转移参量。

9.衰减器有吸收衰减器、 截止衰减器和 极化衰减器三种。

10.微波谐振器基本参量有 谐振波长 、 固有品质因数 和等效电导衰减器三种。

二、传输线理论工作状态（7 分）（第二章）在特性阻抗Z 0=200Ω的传输线上，测得电压驻波比ρ=2，终端为电压波节点，传输线上电压最大值 U max =10V ，求终端反射系数、负载阻抗和负载上消耗的功率。

解： Γ = ρ -1 = 12ρ +1 3由于终端为电压波节点，因此Γ =- 123由Γ =Z L - Z 0= - 12+ Z 3 可得，Z L =100Ω 负载吸收功率为P 2Z 0 ρ三、Smith 圆图（10 分）（第二章）已知传输线特性阻抗Z 0=75Ω，负载阻抗Z L =75+j100Ω，工作频率为 900MHz ，线长l =0.1m ，试用Smith 圆图求距负载最近的电压波腹点与负载的距离和传输线的输入阻抗Z 0Z L解：由工作频率为900 MHz，可得λ=1 m 3而线长为l=0.3λ1.计算归一化负载阻抗ZL=ZLZ= 1+j1.33在阻抗圆图上找到 A 点。

《微波技术基础》题集一、选择题（每题2分，共20分）1.微波是指频率为（）的电磁波。

A. 300MHz-300GHzB. 300Hz-300MHzC. 300GHz-300THzD. 300kHz-300MHz2.微波在真空中的传播速度与（）相同。

A. 光速B. 声速C. 电场传播速度D. 磁场传播速度3.微波的主要特性不包括（）。

A. 直线传播B. 穿透性强C. 反射性D. 绕射能力强4.微波传输线主要包括（）。

A. 同轴电缆和光纤B. 双绞线和同轴电缆C. 光纤和波导D. 双绞线和波导5.在微波通信中，常用的天线类型是（）。

A. 偶极子天线B. 抛物面天线C. 环形天线D. 螺旋天线6.微波谐振腔的主要作用是（）。

A. 储存微波能量B. 放大微波信号C. 转换微波频率D. 衰减微波信号7.微波加热的原理是（）。

A. 微波与物体内部的分子振动相互作用B. 微波使物体表面温度升高C. 微波直接转化为热能D. 微波引起物体内部化学反应8.微波在介质中的传播速度与介质的（）有关。

A. 密度B. 介电常数C. 磁导率D. 温度9.微波通信中，为了减少信号的衰减，通常采取的措施是（）。

A. 增加信号频率B. 减小信号功率C. 使用中继站D. 改用光纤通信10.微波测量中，常用的仪器是（）。

A. 示波器B. 微波功率计C. 万用表D. 频谱分析仪（部分功能重叠，但更专用于频率分析）二、填空题（每题2分，共20分）1.微波的频率范围是_________至_________。

2.微波在真空中的传播速度约为_________m/s。

3.微波的_________特性使其在雷达和通信系统中得到广泛应用。

4.微波传输线中，_________具有宽频带、低损耗的特点。

5.微波天线的作用是将微波能量转换为_________或相反。

6.微波加热过程中，物体吸收微波能并将其转化为_________。

7.微波在介质中的衰减主要取决于介质的_________和频率。

10
i( z, t )
L1 z
R1 z
G1z
i(z z,t)
C1z (z z, t)
( z, t )
z
线元Δz 上的电压、电流的变化为：
z, t z, t z z, t z z
i z, t i z, t i z z , t z z
f ( x) f ( x0 ) f ( x0 )( x x0 ) f ( x0 ) ( x x0 ) 2 2! f ( n ) ( x0 ) ( x x0 ) n Rn ( x) n! Sch.EIE Hefei Normal University

12/3/2018
3
Sch.EIE Hefei Normal University
第二章 传输线理论
2.1 传输线方程 2.2 分布参数阻抗 2.3 无耗线工作状态分析
2.4 有耗线的特性与计算
2.5 史密斯圆图 2.6 阻抗匹配
12/3/2018
4
Sch.EIE Hefei Normal University
传输线理论
i z, t z, t z G1z ( z, t ) C1z z t
12
12/3/2018
Sch.EIE Hefei Normal University
z, t i z, t z R1z i( z, t ) L1z z t
D D2 d 2 / ln d
2 Rs d
C1 ( F / m)
W
d 2 Rs W W d
R1 ( / m)
2 2 D D d G1 (S / m) / ln d 导体表面电阻 Rs 复介电常数 j

（3） ab
1 b 4 ， 1 b 3
bc cd
1 c 4， 1 c 1 d 2 1 d
四． （共 20 分，每小题 10 分）圆图完成（要求写清必要步骤） 1 ． 在 特 性 阻 抗 Z 0 500 的 无 耗 传 输 线 上 ， 测 得 U
六． （10 分）一微波元件的等效网络如图所示，利用网络级联方法计算当 理想传输线 为何值时，网络不引起反射。
解：将等效网络分解为 3 个网络的级联，归一化传输矩阵分别为
cos A 1 j sin
1 j sin ， A2 cos 0
2． 已知传输线的特性阻抗为 50Ω，终端接阻抗为 Z L 25 j 75 的负 载，采用并联单支节匹配，确定支节的位置 d 和长度 l。 解：负载阻抗归一化
Z Z 0.5 j1.5 Z L L 0
在阻抗圆图上找到负载对应的A点，沿等驻波系数圆旋转 180o，得到B点， 可读出负载的归一化导纳为
即当 1、2 端口反相输入时，1、2 端口的输出为零，3 端口有“和”输出，4 端口为零输出。
6
七． （10 分）写出匹配双 T 的 S 矩阵，分析 4 个端口的匹配、隔离、平分 特性；并求当 1、2 端口反相输入时，各个端口的输出为多少？ 解：匹配双 T 的 S 矩阵为
0 0 1 1 0 0 1 S 2 1 1 0 1 1 0
1 1 0 0
匹配特性：如果 3、4 端口匹配，则 1、2 端口自动匹配 隔离特性：由S 12 =S 21 =0，可知 1、2 端口隔离，同理，由S 34 =S 43 =0，可知 3、4 端口隔离， 平分特性： 由S 31 =S 41 =

无线电频段的划分 频段 甚低频 低 中 高 频 频 频 VLF—Very Low Frequency LF—Low Frequency MF—Medium Frequency HF—High Frequency VHF—ery High Frequency UHF—Ultra High Frequency SHF—Super High Frequency EHF—Extreme High Frequency SEHF—Super Extreme High 超极高频 Frequency 300GHz-3THz 0.1-1mm 频率 10KHz-30KHz 30KHz-300KHz 300KHz-3MHz 3MHz-30MHz 30MHz-300MHz 300MHz-3GHz 3GHz-30GHz 30-300GHz 波长 10-100Km 1-10Km 100m-1Km 10-100m 1-10m 10cm-1m 1cm-10cm 1mm-1cm
——微波技术基础的先修课程包括：
高等数学、线性代数、复变函数、矢量分析、电子线路、电磁场与电磁波等。
——微波技术基础课程内容包括：
第 0 章绪论 0.1 电磁波谱及微波；0.2 微波的特点及其应用；0.3 微波技术的发展；0.4 微波技术的研究方 法和基本内容 第 1 章传输线理论 1.1 引言；1.2 传输线波动方程及其解；1.3 均匀无耗传输线的特性参量；1.4 均匀无耗传输线 的工作状态；1.5 阻抗圆图和导纳圆图；1.6 阻抗匹配。 第 2 章规则波导 2.1 规则波导传输的一般理论；2.2 矩形波导；2.3 圆形波导；2.4 同轴线及其高次模；2.5 特殊 波导简介。 第 3 章平面传输线
察到了驻波并证实与实验设备尺寸有关。 1933 年 Southworth 和他的同事们在 AT&T 通过 6m 长的波 导发射并接收到了电报信号。 其后，在微波技术领域的另一个重要进展是在 1937 年研制出了产生连续微波的源，称为速调 管（Klystron） 。这种微波真空管是由 Sperry Gyroscop Company 资助，在 Stanford 由 Russell，Sigurd Varian 和 William Hansen 发明的。 它们的目的是希望研制出用于飞机在恶劣天气情况下的着陆设备。 同时，一些公司（如 AT&T，ITT，Marconi）则资助用于通信系统的微波研究。 由于这些在二战前的研究，无线电探测与定位－雷达（radar）激励人们对微波研究迅速增加。 大多数现在使用的微波器件都是在二战期间在英国、 美国和战争实验室里研制的。 关于这段时间微 波技术的发展历史，在由 MIT Radiation Laboratory 成员所撰写的 28 卷文件中有详细的叙述。

题 解第 一 章1-1 微波是频率很高，波长很短的一种无线电波。

微波波段的频率范围为8103⨯Hz~12103⨯Hz ，对应的波长范围为1m~0.1mm 。

关于波段的划分可分为粗分和细分两种。

粗分为米波波段、分米波波段、厘米波波段、毫米波波段、亚毫米波段等。

细分为Ka K Ku X C S L UHF 、、、、、、、…等波段，详见表1-1-2。

1-2 简单地说，微波具有下列特点。

（1） 频率极高，振荡周期极短，必须考虑系统中的电子惯性、高频趋肤效应、辐射效应及延时效应；（2） 波长极短，“反射”是微波领域中最重要的物理现象之一，因此，匹配问题是微波系统中的一个突出问题。

同时，微波波长与实验设备的尺寸可以比拟，因而必须考虑传输系统的分布参数效应；（3） 微波可穿透电离层，成为“宇宙窗口”；（4） 量子特性显现出来，可用来研究物质的精细结构。

1-3 在国防工业方面：雷达、电子对抗、导航、通信、导弹控制、热核反应控制等都直接需要应用微波技术。

在工农业方面，广泛应用微波技术进行加热和测量。

在科学研究方面，微波技术的应用也很广泛。

例如，利用微波直线加速器对原子结构的研究，利用微波质谱仪对分子精细结构进行研究，机载微波折射仪和微波辐射计对大气参数进行测量等等。

第 二 章2-1 解 ∵01011Z Z Z Z +-=Γ 2-2 解 图（a ）的输入阻抗021Z Z ab =； 图（b ）的输入阻抗0Z Z ab =；图（c ）的输入阻抗0Z Z ab =；图（d ）的输入阻抗052Z Z ab =； 其等效电路自绘。

2-3 解 ∵01011Z Z Z Z +-=Γ 2-4 解 （1） ∵e j Z Z Z Z 40101122π=+-=Γ （2） ∵π2 =l β2-5 解 ∵ljZ Z l jZ Z Z Z tg βtg β10010++= 2-6 证明而I Z E I Z E U g 0-=-= 故2EU =+2-7 证明而 ρ11min =Z ，对应线长为1min l 故 1min 11min 1tg β1tg βρ1l Z j l j Z ++= 整理得 1min 1min 1tg βρρtgβ1l j l j Z --=2-8 解而给定的1Z 是感性复阻抗，故第一个出现的是电压腹点，即λ/4线应接在此处。

微波技术基础课后习题答案
1
1.8由于终端负载的入射波电压复振幅为25V，反射波电压复振幅为2.5V，因此
当距离终端负载 处时，
当距离终端负载 处时，
电压波的瞬时表达式为：
电流波的瞬时表达式为：
1.15
（e）终端阻抗 经过两个 阻抗变换之后输入阻抗仍为 ，另一支路在支节点处输入阻抗仍为 ，所以支节点处等效输入阻抗为 ；再经 阻抗变换得输入端输入阻抗为 ，反射系数 ；
1.16 ， ，距离负载 处阻抗
， 的实部等于 ，
根据传输线导纳公式：
根据单支节在传输线上的匹配条件： 的实部应为 ，因此：
， 或
当 时，单支线在主线 处（即终端负载处），此处 。因此短路支节导纳为 ，所以 ，支节长度 。
当 时，单支线在主线 处，此处 。所以短路支节导纳为 ，所以 ，支节长度 。
1.18将终端负载阻抗变为导纳得到 。若并联支线长度为 ，那么 ，因此 。可以得到并联分支线的最短长度为 。并联分支线后的终端负载为 ，因此 变换线的特性阻抗为 。
解：由图可知 ；
；所以 ；
1、传输线的特性阻抗为 ，行波系数为 ，第一电压波节点距离终端负载为 ，请写出终端负载 的表达式。
解：行波系，
2、试证明终端负载 与反射系数 存在如下关系：
， ，其中 为传输线的特性阻抗。
答：
因此 ，
3、已测得一无耗传输线的各项指标如图所示，试求负载阻抗 、ρ、λ。

第二章习题参考答案2.32（4）把史密斯圆图作为导纳圆图，则实轴最右端的点代表短路点，对应向电源λ25.0。

在最外层圆上找到点3.1j -，对应向电源为λ354.0，所以短路支节长度λλλ104.025.0354.0=-=l2.33（1）在史密斯圆图上找到8.04.0j z L +=对应的点A ，连接OA 对应向电源λ114.0。

沿以O 为原点，OA 为半径，即沿等Γ圆向电源（顺时针方向）旋转λλ136.0)114.025.0(=-到达正实轴上的点B ，点B 电表电压驻波最大点，所以λ136.0max =d 。

同理，沿以O 为原点，OA 为半径，即沿等Γ圆向电源（顺时针方向）旋转λλ386.0)114.05.0(=-到达负实轴上的点C ，点C 电表电压驻波最小点，所以λ386.0min =d 。

B 点对应的阻抗为2.4，等于电压驻波比2.4≈VSWRC 点对应的阻抗约为24.0，等于电压驻波比的倒数24.01≈=VSWRK （3）负实轴上的点代表电压驻波比的倒数32.01≈=VSWRK ，在负实轴上找到对应0.32的点A 。

然后沿以O 为原点，OA 为半径，即沿等Γ圆向负载（逆时针方向）旋转λ32.0到达点B ，连接OB 对应向电源λλλ18.032.05.0=-。

B点对应的为归一化负载阻抗4.12.1j z L +=，所以负载阻抗为Ω+=+=+=10590)4.12.1(75)4.12.1(0j j j Z Z L然后沿以O 为原点，OB 为半径，即沿等Γ圆向电源（顺时针方向）旋转λ29.0到达点C ，则C 点对应的归一化阻抗18.032.0j -，所以输入阻抗Ω-=-=5.1324)18.032.0(0j j Z Z in 2.35)](1[22)()](1[)](1[222)(00000000d e Z V e Z Z I V e Z Z I V d I d e V d e Z I V e Z I V e Z I V d V dj L d j L L d j L L d j L dj L L d j L L d j L L Γ-=--+=Γ+=Γ++=-++=+-+-βββββββ)2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==Γ选取电压驻波最大点值点距负载的距离用max d 表示，此时有 ]1)[()(max max L d V d V Γ+=+]1)[()(max max L d I d I Γ-=+所以VSWR Z d I d V d I d V d Z L L in 0max max max max max ]1)[(]1)[()()()(=Γ-Γ+==++dtg d jZ Z dtg jZ d Z Z Z d tg jZ Z d tg jZ Z Z d Z in inL L L in ββββ)()()(000000--=⇒++= maxmaxmax max 0max 0max 01)()(d jVSWRtg d jtg VSWR Z Z d tg d jZ Z d tg jZ d Z Z Z L in in L ββββ--=⇒--= 把Ω=1250Z ，cm d 15max =，5=VSWR ，41.2)15802(max ==πβtg d tg 代入上式可得：45.4910.2941.25141.251251max max 0j j j d jVSWRtg d jtg VSWR Z Z L +=⨯--=--=ββ2.40Ω=20L Z 通过cm d 0.5=的传输线变换到阻抗为：)(125)())5202(,50,20()(201010000Ω==⇒=Ω==Ω=++=Lin L L L in Z Z d Z tg d tg Z Z Z d tg jZ Z d tg jZ Z Z d Z πβββ把变换阻抗)(125)(20Ω==Lin Z Z d Z 作为新的负载阻抗再进行阻抗变换可得：)(47.2656.80)())8.12202(,90,125()(020000Ω-=⇒=Ω==Ω=++=j d Z tg d tg Z Z Z d tg jZ Z d tg jZ Z Z d Z in L L L in πβββ把变换阻抗)(125)(20Ω==Lin Z Z d Z 作为新的负载阻抗可得左边部分的终端反射系数为：437)90,125(000=Γ⇒Ω=Ω=+-=ΓL L L L L Z Z Z Z Z Z d j L d j L L d j L L L L d j L d j L d j L L d j L L e e Z Z Z Z d eZ I V Z I V V V d e V e V e Z I V e Z I V d V βββββββ220020000)()(22)(---+---+-Γ=+-=Γ⇒⎪⎪⎭⎪⎪⎬⎫+-==Γ+=-++=16.003.0)8.122042,437()8.12(2j d e cm d L d j L +-===ΓΓ==Γ-πββ 2.47已知终端短路传输线的输入阻抗为：d tg jZ d Z scin β0)(= 则归一化阻抗为：d jtg Z d Z d z scin sc inβ==0)()(归一化导纳为：d jctg d Y Z d Z Z d z d y scin scin sc in scin β-====)()()(1)(00 （1）：并联的短路支节的归一化导纳为：9.0)7.045.0()2.045.0(j j j -=+--所以有：13.09.01219.0)(==⇒-=-=arctg dd jctg j d y scinπλβ （2）：并联的短路支节的归一化导纳为：5.0)7.045.0()2.045.0(j j j -=+-+所以有：18.05.01219.0)(==⇒-=-=arctg dd jctg j d y scinπλβ 2.48(如图)：已知：dtg jZ Z d tg jZ Z Z d Z L L in ββ++=000)(把Ω+=250300j Z L ，Ω=5000Z ，d tg t β=代入上式可得：]}300)250500)(500250[()]500250(300)250500(300{[)300()250500(500)250300(500500250300500)(222000t t t j t t t t t t j j t j j d tg jZ Z d tg jZ Z Z d Z L L in --++++-+-⇒++++=++=ββ令0)](Im[=d Z in ，则可得：⇒=--+0300)250500)(500250(2t t t ⎩⎨⎧=-=4634.16834.021t t 所以接入的位置为：405.0)(2111=+=t acrtg d λ155.0)(22==t acrtg d λ取接入点距负载最小处，λ155.0=d ，4634.1==d tg t β，1118)155.0(==λd Z in接入四分之一波长变换器的特性阻抗为：)(6.747111850001Ω=⨯=Z 史密斯圆图解法：在圆图上找到归一化负载阻抗5.06.05002503000j j Z Z z L L +=+==的对应点A ，连接OA 对应的向电源λ094.0。

25 - j17.5
0.01 - j 0.02 0.003 - j 0.032 27.5 j12 9.4 j 22.4
4.12 d 4.13
0.125 和 l 0.127
解 1： d1
0.456 和 l1 0.432 0.091 和 l2 0.067 0.39 和 l2 0.33 0.44 和 l2 0.40 0.14 和 l2 0.07
解 2： d 2 4.14
（1） 解 1： l1
解 2： l1 （2） 解 1： l1
解 2： l1 （3） 解 1： l1 解 2： l1 （4）
0.25 和 l2 0.43 0.36 和 l2 0.41 0.14 和 l2 0.33
l1 0.22 和 l2 0.09
0.125 和 l2 0.44
（5） 解 1： l1 解 2： l1
0.07 和 l2 0.04
0.198 和 l2 0.14
（6） 解 1： l1 解 2：
l1 0.125 和 l2 0.36
4.18
( )
2
2
ln
Z0 cos L 2 Z L ( 2 L) 2
2 2 50(3 2 2) () 2 1 2 Z 50 50(3 2 2) () 或 Z ( z1 ) Z0 0 k 3 2 2 1
3.10 Z L 50 3.11
1 j1.336 39.57e j 34.71 2 j 0.668
Z L jZ0tg ( d ) 38.24+j3.14 Z0 jZ L tg ( d )
4.8
in

《微波技术与天线》课后部分习题解答
1 第二章
2-3 传 输 线 电 路 图 如 图1所 示 。 问 ： 图a中ab间 的 阻 抗Zab = 0对 吗 ？ 图b中ab间 的阻抗Zab = ∞对吗？为什么？ 解：
图 1: 题2-3图
Zin(z)
=
Z0
ZL Z0
+ jZ0tan(βz) + jZLtan(βz)
所以传输线上的电流、电压分布如图10所示。 2-31 ( ) 传输线阻抗匹配的方法有哪几种？哪些是窄频带的？哪些是 宽频带的？ 答：
传输线阻抗匹配的方法主要有：λ/4阻抗变换器；宽带λ/4阻抗变换器；支 节匹配器和渐变匹配器。 其中λ/4阻抗变换器、 支节匹配器是窄带匹配； 宽带λ/4阻抗变换器、渐 变匹配器是宽带匹配；
(24)
所以有
ρ
=
ZL + jZ0tan(βz) Z0 + jZLtan(βz)
=
2
(25)
将z = λ/12，ZL = √RL + jXL，Z0 = 70代入式(25)中得： RL = 80，XL = 30 3
2-21 (√ ) 传输线长λ，特性阻抗为Z0，当终端负载分别为ZL = Z0,ZL = 0,ZL = j 3Z0时。 (1)计算相应的终端反射系数和驻波比； (2)画出相对电压振幅|U/U +|、相对电流振幅|I/I+|的沿线分布并标出其最
(20)
Γ
=
RL RL
− Z0 + Z0
当RL > Z0时 ，Γ(z)为 正 实 数 ， 终 端 为 电 压 的 波 腹 点 ， 则 有RL = Z0ρ，所以ρ = RL/Z0 当RL < Z0时，Γ(z)为负实数，终端为电压的波节点，则有RL = Z0/ρ，所 以ρ = Z0/RL 证毕。

电磁场与微波技术第一二三章课后习题及部分答案第 1 章习题1、求函数()D Cz By Ax u +++=1的等值面方程。

解：根据等值面的定义：标量场中场值相同的空间点组成的曲面称为标量场的等值面，其方程为)( ),,(为常数c c z y x u =。

设常数E ，则，()E D Cz By Ax =+++1，即：()1=+++D Cz By Ax E针对不同的常数E （不为0），对应不同的等值面。

2、已知标量场xy u =，求场中与直线042=-+y x 相切的等值线方程。

解：根据等值线的定义可知：要求解标量场与直线相切的等值线方程，即是求解两个方程存在单解的条件，由直线方程可得：42+-=y x ，代入标量场C xy =，得到： 0422=+-C y y ，满足唯一解的条件：02416=??-=?C ，得到：2=C ，因此，满足条件的等值线方程为：2=xy3、求矢量场z zy y y x xxy A 222++=的矢量线方程。

解：由矢量线的微分方程：zy x A dz A dy A dx ==本题中，2xy A x =，y x A y 2=，2zy A z =，则矢量线为：222zy dzy x dy xy dx ==，由此得到三个联立方程：x dy y dx =，z dz xdx =，zy dzx dy =2，解之，得到： 22y x =，z c x 1=，222x c y =，整理，y x ±=，z c x 1=，x c y 3±=它们代表一簇经过坐标原点的直线。

4、求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy x x t ?3??242+-=方向的方向导数。

解：由标量场方向导数的定义式：直角坐标系下，标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zuy u x u l u ??+??+??=??α、β、γ分别是l 方向的方向角，即l 方向与z y x、、的夹角。