南京信息工程大学 13-14线性代数期末

线性代数期末考试题及答案一、选择题1. 下列哪个不是线性代数的基本概念？A. 矩阵B. 向量C. 函数D. 行列式答案：C. 函数2. 矩阵A的转置记作A^T，则（A^T）^T等于A. AB. -AC. A^TD. 2A答案：A. A3. 对于矩阵A和B，满足AB = BA，则称A和B是A. 相似矩阵B. 对角矩阵C. 线性无关D. 对易矩阵答案：D. 对易矩阵4. 行列式的性质中，不能成立的是A. 行列式交换行B. 行列式某一行加上另一行不变C. 行列式等于数乘其中某一行对应的代数余子式的和D. 行列式的某一行的系数乘以另一行不变答案：D. 行列式的某一行的系数乘以另一行不变5. 给定矩阵A = [3, -1; 4, 2]，则A的秩为A. 0B. 1C. 2D. 3答案：C. 2二、填空题1. 给定矩阵A = [2, 1; -3, 5]，则A的行列式为______答案：132. 设矩阵A的逆矩阵为A^-1，若AA^-1 = I，其中I是单位矩阵，则A的逆矩阵为______答案：I3. 若矩阵的秩为r，且矩阵的阶数为n，若r < n，则该矩阵为______矩阵答案：奇异三、简答题1. 解释什么是线性相关性和线性无关性？答案：若存在不全为零的数k1, k2，...，kn，使得方程组中的向量k1v1 + k2v2 + ... + knvn = 0成立，则称向量组{v1, v2, ..., vn}线性相关；若该方程仅在k1 = k2 = ... = kn = 0时成立，则称向量组{v1, v2, ..., vn}线性无关。

2. 如何判断一个矩阵是对称矩阵？答案：若矩阵A的转置等于自身，即A^T = A，则称矩阵A是对称矩阵。

四、计算题1. 给定矩阵A = [1, 2; 3, 4]，求A的逆矩阵。

答案：A的逆矩阵为1/(-2)[4, -2; -3, 1]2. 求向量v = [1, 2, 3]的模长。

常 微 分 方 程 练 习 题（一）注：此练习与考试内容无关，仅作复习参考。

考试试卷是从题库中随机抽取。

一、填空题1. 微分方程()dy p x y dx=的通解为_______________________. 2．在变换y u x =下， 方程sin dy x dx y =可化为关于未知函数为()u u x =的方程为 。

3．在变换u x y =+下， 方程()x y dy e dx +=可化为关于未知函数为()u u x =的方程为 。

4．与积分方程⎰+=xx dx y x f y y 0),(0等价的微分方程的初值问题是 .5. 初值问题0)0(,12=+=y y dxdy 的解的最大存在区间为________________. 6. 写出Cauchy问题()10dy dx y ⎧=⎪⎨⎪=⎩_______________________.7. 若i x ，1,2,,,i n =为n 阶齐次方程()(1)1()()0n n n x a t x a t x -+++=的n 个线性无关解，则这一齐次方程的通解可表示为____________________________________________.8. 试将二阶方程22232sin d x dx t tx t dt dt+-=化为方程组 ______________________. 9. 函数组t t t e e e 2,,-的朗斯基行列式是 .10．欧拉方程222220d y dy x x y dx dx --=在变换t e x =下,可化为______________________. 11．设n 阶方程组Ax dtdx =的基解矩阵为()t Φ,其中A 为n 阶实矩阵, 则=At exp ________________.12.若()t Φ是'()x A t x =的基解矩阵，则'()()x A t x f t =+满足0()x t η=的解________________________________________.13．方程133dy y dx=过（0，0）点存在_______________________个解。

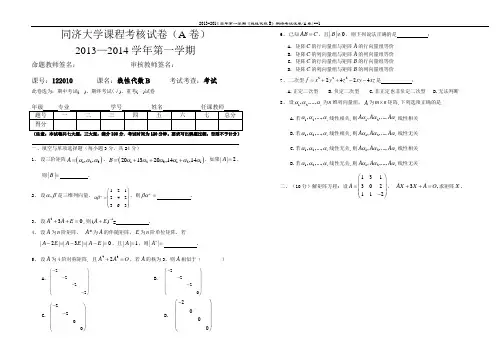
同济大学课程考核试卷（A 卷）2013—2014学年第一学期命题教师签名： 审核教师签名：课号：122010 课名：线性代数Ｂ 考试考查：考试此卷选为：期中考试( )、期终考试(√)、重考( )试卷（注意：本试卷共七大题，三大张，满分100分．考试时间为120分钟。

要求写出解题过程，否则不予计分）一、填空与单项选择题（每小题3分，共24分）1、 设三阶矩阵()123,,A ααα=，()123121201320,14,14B αααααα=+++，如果||2A =， 则||B = .2、 设,αβ是三维列向量，121242363T αβ⎛⎫⎪= ⎪ ⎪⎝⎭，则T βα= .3、 设230A A E ++=,则1()A E -+= .4、 设A 为n 阶矩阵， *A 为A 的伴随矩阵，E 为n 阶单位矩阵. 若|2||3|||0A E A E A E -=-=-=，且||1A =，则*||A = .5、 设A 为4阶对称矩阵, 且432A A O +=，若A 的秩为3，则A 相似于（ ）A ．2222-⎛⎫ ⎪- ⎪ ⎪- ⎪-⎝⎭B ． 2220-⎛⎫⎪- ⎪ ⎪- ⎪⎝⎭ C. 2200-⎛⎫⎪- ⎪ ⎪ ⎪⎝⎭D. 2000-⎛⎫⎪⎪ ⎪ ⎪⎝⎭6、 已知AB C =，且||0B ≠，则下列说法正确的是 ： A. 矩阵C 的行向量组与矩阵A 的行向量组等价 B. 矩阵C 的列向量组与矩阵A 的列向量组等价 C. 矩阵C 的行向量组与矩阵B 的行向量组等价D. 矩阵C的列向量组与矩阵B 的列向量组等价7、 二次型2222424f x y z xy xz =++--是 ：A.正定二次型B.负定二次型C.非正定也非负定二次型D.无法判断 8、 设12,,...,s ααα为n 维列向量组，A 为m n ⨯矩阵,下列选项正确的是 A.若12,,...,s ααα线性相关,则12,,...,s A A A ααα线性相关B.若12,,...,s ααα线性相关,则12,,...,s A A A ααα线性无关C.若12,,...,s ααα线性无关,则12,,...,s A A A ααα线性相关D.若12,,...,s ααα线性无关,则12,,...,s A A A ααα线性无关二、（10分）解矩阵方程: 设131302112A ⎛⎫⎪= ⎪ ⎪-⎝⎭， 3,AX X A O ++=求矩阵X .三、（12分）已知向量组：11 2 3 1α⎛⎫⎪⎪=⎪⎪⎝⎭，22121α⎛⎫⎪⎪=⎪-⎪-⎝⎭，34541α⎛⎫⎪⎪=⎪⎪⎝⎭，43212α⎛⎫⎪⎪=⎪⎪⎝⎭，512α⎛⎫⎪⎪=⎪⎪-⎝⎭，求该向量组的秩及一个最大线性无关组，并将不属于最大线性无关组的向量用该最大线性无关组线性表示.（13分）问当λ为何值时, 线性方程组123123123(1)3(1)3(1)0x x xx x xx x xλλλλ-++=⎧⎪+-+=⎨⎪++-=⎩有唯一解、无解、有无穷多解? 并在有无穷多解时求出其通解. 五、（15分）求一个正交变换,x Py=把二次型2213122322f x x x x x x=++-化为标准形，并写出标准形．六、（10分）设2()M 为所有二阶方阵按照通常矩阵的加法和数乘运算构成的线性空间. 给定可逆矩阵2()P M ∈ ，在2()M 上定义如下相似变换：对任意2()A M ∈ ,1()T A P AP -=. (1) 证明：映射T 是2()M 上的一个线性变换；(2）若1112P ⎛⎫= ⎪⎝⎭，求出线性变换T 在基111221221001000000001001E E E E ⎛⎫⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，，，下的矩阵．七、证明题:(1)（6分）设A 是n m ⨯矩阵, B 是m n ⨯矩阵, E 是n 阶单位矩阵. 若AB E =，证明矩阵B 的列向量组线性无关.(2)（10分)设矩阵2,T T A ααββ=+其中,αβ是两个互相正交的三维单位列向量. 证明：矩阵A 能够相似于对角矩阵1=20⎛⎫ ⎪Λ ⎪ ⎪⎝⎭.。

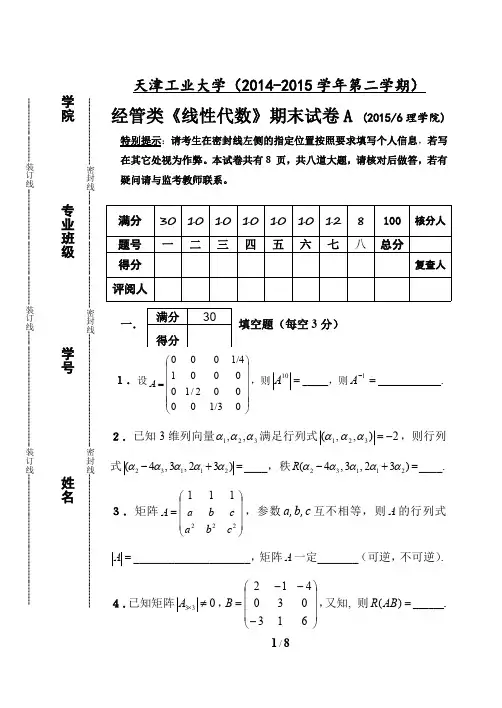
南京信息工程大学真的信号与系统真题注意：本文遵守百度文库规定，非作广告用途，只是展示南信大信号与系统真题试卷和真实情况，让大家更好的识别市面上假的真题试卷，回归到复习的正确道路上来1、板块一：展示假的最近三年的真题市面上流行的本校假的考研2012年真题最近两年两年出现了南京信息工程大学信号与系统的假的真题，为防止各位考生上当受骗，现作为该校的研究生晒出市面上假的信号与系统的真题一、假版本一（完全的假货）此版本出自淘宝卖家为北京的店家，坑害了一大批买者南京信息工程大学2012年攻读硕士学位入学考试试题考试科目：信号与系统科目代码814（注：答案必须写在答题纸上，写在试题上无效）一、选择题（每题2分，共20分）1.下列信号的分类方法不正确的是（）：A、数字信号和离散信号B、确定信号和随机信号C、周期信号和非周期信号D、因果信号与反因果信号2.下列说法正确的是（）：A、两个周期信号x(t)，y(t)的和x(t)+y(t)一定是周期信号。

B、两个周期信号x(t)，y(t)的周期分别为2和2，则其和信号x(t)+y(t)是周期信号。

C 、两个周期信号x (t )，y (t )的周期分别为2和π，其和信号x (t )+y(t )是周期信号。

D 、两个周期信号x (t )，y (t )的周期分别为2和3，其和信号x (t )+y(t )是周期信号。

3.下列说法不正确的是（）。

A 、一般周期信号为功率信号。

B 、时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。

C 、ε(t )是功率信号；D 、e t 为能量信号;4.将信号f (t )变换为（）称为对信号f (t )的平移或移位。

A 、f (t –t 0)B 、f (ｋ–k 0)C 、f (at )D 、f (-t )5.将信号f (t )变换为（）称为对信号f (t )的尺度变换。

A 、f (at )B 、f (t –k 0)C 、f (t –t 0)D 、f (-t )6.下列关于冲激函数性质的表达式不正确的是（）。

南京信息工程大学高等数学试卷参考答案及评分标准一 填空题（本题共5小题，每小题3分，满分15分）1．设z y x xy z y x z y x f 42432),,(222-+-+++=求gradf(0,0,0)= -4i+2j-4k2．向量α 和β 构成的角3πϕ=，且8,5==βα ，则βα +=1293．=→→xxy a y x )sin(lim 0 a 4．C 为依逆时针方向绕椭圆12222=+b y a x 的路径,则⎰--+C dy y x dx y x )()(= ab π2-5．微分方程)1(2+='y x y 的通解是12-=x ce y二 选择题（本题共5小题，每小题3分，满分15分）1．直线L ： 37423zy x =-+=-+ 与平面3224=--z y x 的关系是[ A] A ．平行 B ．直线L 在平面上C ．垂直相交D ．相交但不垂直2．y x z 2+=在满足522=+y x 的条件下的极小值为[ ]A ．5B ．-5C ．52D ．-523．设∑为球面2222R z y x =++,则⎰⎰∑++ds z y x )(222=[ C ]A ．dr r r d d Rϕϕθππsin 200022⎰⎰⎰⋅ B. dv R ⎰⎰⎰Ω2 C ． 44R π D.534R π4．级数n i nnx ∑∞=-+12)1(2的收敛半径是 [ D ] A ．23B ．61C ．23或 61D ．25．x xe y y y y =+'+''+'''的通解形式为y= [ A ]A ． x e b ax )(+B ． x e b ax x )(+C ． x e b ax x )(2+D ． []x d cx x b ax e x 2sin )(2cos )(+++三 求下列各题（本题共3小题，每小题10分，满分30分）1． 计算d x d y y y D ⎰⎰sin D ：2y x = 和 x y = 所围成的区域。

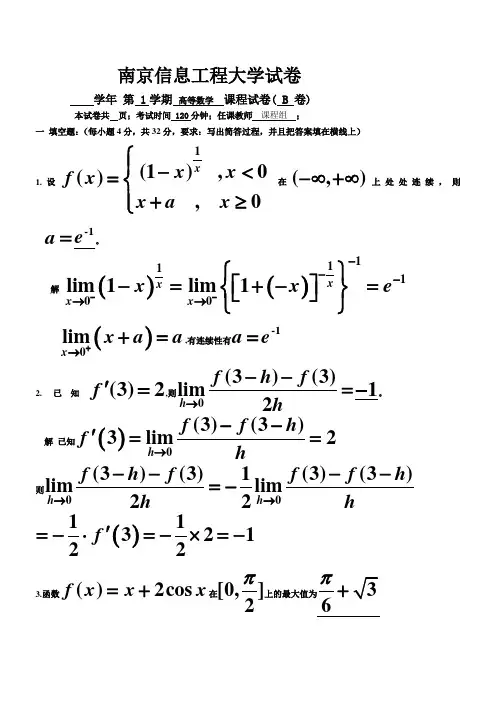
南京信息工程大学试卷学年 第 1学期 高等数学 课程试卷( B 卷)本试卷共 页；考试时间 120分钟；任课教师 课程组 ；一 填空题：（每小题4分，共32分，要求：写出简答过程，并且把答案填在横线上）1.设1(1),0(),xx x f x x a x ⎧⎪-<=⎨⎪+≥⎩在(,)-∞+∞上处处连续，则a =-1e。

解()()1111lim 1lim 1x xx x x x e-----→→⎧⎫⎡⎤-=+-=⎨⎬⎣⎦⎩⎭()0lim x x a a +→+=,有连续性有a =-1e2. 已 知(3)2f '=,则0(3)(3)lim2h f h f h →--=1-。

解 已知()0(3)(3)3lim2h f f h f h →--'==则(3)(3)1(3)(3)limlim22h h f h f f f h h h→→----=-()1132122f '=-⋅=-⨯=-3.函数()2cos f x x x =+在[0,]2π上的最大值为6π+解 令()12sin 0f x x '=-=得6x π=()026622f f f ππππ⎛⎫⎛⎫==+=⎪ ⎪⎝⎭⎝⎭则最大值为6π+4. 设5(sin )5(1cos )x t t y t =+⎧⎨=-⎩ ， 则t dydx==0,22t d y dx==120解()5sin 051cos t t t dydyt dt dx dxt dt======+22t t t dy d dy dx d d y dx dt dxdxdxdt===⎛⎫ ⎪⎛⎫⎝⎭ ⎪⎝⎭==()()()22cos 1cos sin 1cos 151cos 20t t t tt t =+++==+5. 设1(0)xy xx +=>，则y '=()1ln xx x x x ++解 两边取对数有()ln 1ln y x x =+两边关于x 求导得1ln y x x yx'+=+,整理后即得结果6. 设函数()y y x =由方程cos()0x y xy ++=确定，则dy =sin 11sin y xy dx x xy--。

第 1 页 共 3 页∞∞∞= ⎰ ⎰ 南京信息工程大学 试卷2020－2021 学年 第二学期 高等数学Ⅱ（2） 课程期末试卷( A 卷)考试时间 120 分钟； 出卷时间 2021 年 6 月； 文科各专业 适用一、填空题 (每小题 3 分，共 15 分)(1) 向量a = (1, -2,5) 在向量b = (1, -2, 2) 上的投影为 . (2) 极 限 limsin( xy )= .x →0y →1(3) 函 数 z = (x - y )3+ 2x - 2 y ， 则∂z + ∂z = .∂x ∂y(4) 过点(1,1, 0) 且垂直于平面2x - y + 3z + 5 = 0 的直线方程为 .(5) 微分方程 y ' - y = e x满足y |x =0 = 2 的特解为 ........................ 二、选择题 (每小题 3 分，共 15 分)(1) 设a = (3, -5,8) ， b = (-1,1, x ) ，且a ⊥ b ，则 x = （ ）(A ) 0 (B ) 3 (C ) 2 (D ) 1(2) 函数 z = sin(x - 2 y ) 在点 M (π , π) 6处的全微分dz = （）(A ) - cos(x - 2 y ) (B ) - 1dx + dy2 (C ) cos(x - 2 y )dx - 2 cos(x - 2 y )dy (D ) 12(3) 下列级数中收敛的是 ()(A )∑1(B)∑(-1)n(C)∑ 1(D ) ∑(- 3)nn =1n 3n =1n =1 n =121 1- y(4) 设 Idy 0f (x , y )dx ，则交换积分次序后（）请将所有答案（含填空、选择）写到《试．卷．答．题．册．》上相应位置！ n学院专业班级姓名学号任课教师…………………………………………………装…………………………………订…………………………………线……………………………………………∞ xM第 2 页 共 3 页= ⎰ ⎰1 131 1- x(A) I 0 dx0 11- x 2f (x , y )dy (B) I = ⎰0 dx⎰0 f (x , y )dy 1 1+ x 2 (C) I = ⎰0dx⎰f (x , y )dy(D) I = ⎰0dx⎰f (x , y )dy(5) 特征方程r2- 2r +1 = 0 所对应的齐次线性微分方程是 ()(A) (A ) y ' - 2 y ' +1 = 0(B ) y ' - 2 y ' + y +1 = 0(C ) y ' - 2 y ' + y = 0 (D ) y ' + y ' - 2 y = 0三、计算题 (每小题 5 分，共 30 分)(1) 设函数满足等式 x - az =f ( y - bz ) ，且 f 为可微函数，求∂z , ∂z . ∂x ∂y(2) 计算二重积分⎰⎰ x 2 y dxdy ，其中 D 由曲线 y = x 2 、直线 x = 1 和 x 轴所围闭 D区域.(3) 求曲面e x + 2 y 2 + 3z 2= 6 在点(0,1,1) 处的切平面方程.∞nn 2(4) 判断级数∑(-1)n的收敛性，若收敛，是绝对收敛还是条件收敛？n =1(5) 求微分方程 y ' - 2 y ' - 3y = 3x +1的通解. (6) 将函数 f (x ) = ln(1+ x ) 展开为 x 的幂级数．四、(本题满分 8 分) 设函数 z = f (x - y , xy ), 且 f (u , v ) 具有连续的二阶偏导数，∂z ∂z ∂2 z 求∂x , ∂y , ∂x ∂y .五、(本题满分 8 分) 求微分方程(1+ x 2) y ' = 2xy '满足初值条件 y |x =0 = 1，y ' |x =0 = 3 的特解.六、(本题满分 8 分) 在平面 x + y + 2z = 2 上求一点，使该点到原点的距离最短，并求出最短距离.第 3 页 共 3 页2n ∞n -1n -1 ∞n -1七、(本题满分 8 分) 求幂级数∑(-1)nxn =1的和函数，并求∑(-1)n ． n =1八、(本题满分 8 分) 设二元函数 f (x , y ) 在区域 D = {(x , y ) | x 2+ y 2≤ 1}上连续，且满足 f (x , y ) = 2(x 2 + y 2) - (x + y +1)⎰⎰ f (x , y )dxdy , 求 f (x , y ) .D。

线性代数期末考试试题及答案线性代数期末考试试题及答案线性代数是一门重要的数学课程，广泛应用于各个领域，如物理学、工程学、计算机科学等。

期末考试是对学生对于线性代数知识的综合考察，下面将给出一些线性代数期末考试试题及答案，供大家参考。

一、选择题（每题2分，共20分）1. 设A是一个3×3矩阵，若A的行列式值为0，则A的秩为：A. 0B. 1C. 2D. 3答案：C2. 设A是一个3×3矩阵，若A的特征值为1，2，3，则A的特征向量个数为：A. 0B. 1C. 2D. 3答案：D3. 设A是一个3×3矩阵，若A的秩为2，则A的零空间的维数为：A. 0B. 1C. 2D. 3答案：B4. 设A是一个3×3矩阵，若A的行向量组线性无关，则A的列向量组是否线性无关？A. 是B. 否答案：A5. 设A是一个3×3矩阵，若A的行向量组线性相关，则A的列向量组是否线性相关？A. 是B. 否答案：A6. 设A是一个3×3矩阵，若A的秩为2，则A的行空间的维数为：A. 0B. 1C. 2D. 3答案：C7. 设A是一个2×2矩阵，若A的特征值为1，2，则A的特征向量个数为：A. 0B. 1C. 2答案：C8. 设A是一个2×2矩阵，若A的特征值为1，1，则A的特征向量个数为：A. 0B. 1C. 2答案：B9. 设A是一个2×2矩阵，若A的秩为1，则A的零空间的维数为：A. 0B. 1C. 2答案：B10. 设A是一个2×2矩阵，若A的秩为2，则A的行空间的维数为：A. 0B. 1C. 2答案：C二、填空题（每题3分，共30分）1. 设A是一个3×3矩阵，若A的行向量组线性无关，则A的秩为____。

答案：32. 设A是一个3×3矩阵，若A的列向量组线性无关，则A的秩为____。

答案：33. 设A是一个3×3矩阵，若A的行向量组线性相关，则A的秩为____。

×××大学线性代数期末考试题一、填空题（将正确答案填在题中横线上。

每小题2分，共10分）1. 若022150131=---x ，则=χ__________。

2．若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解，则λ应满足 。

3．已知矩阵n s ij c C B A ⨯=)(，，，满足CB AC =，则A 与B 分别是 阶矩阵。

4．矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。

5．n 阶方阵A 满足032=--E A A ，则=-1A 。

二、判断正误（正确的在括号内填“√”，错误的在括号内填“×”。

每小题2分，共10分）1. 若行列式D 中每个元素都大于零，则0〉D 。

（ ）2. 零向量一定可以表示成任意一组向量的线性组合。

（ ）3. 向量组m a a a ，，， 21中，如果1a 与m a 对应的分量成比例，则向量组s a a a ，，， 21线性相关。

（ ）4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ，则A A =-1。

（ ） 5. 若λ为可逆矩阵A 的特征值，则1-A 的特征值为λ。

( )三、单项选择题 (每小题仅有一个正确答案，将正确答案题号填入括号内。

每小题2分，共10分)1. 设A 为n 阶矩阵，且2=A ，则=T A A （ ）。

① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα，，， 21（3 ≤ s ≤ n ）线性无关的充要条件是（ ）。

① s ααα，，， 21中任意两个向量都线性无关 ② s ααα，，， 21中存在一个向量不能用其余向量线性表示 ③ s ααα，，， 21中任一个向量都不能用其余向量线性表示④ s ααα，，， 21中不含零向量 3. 下列命题中正确的是( )。

南京信息工程大学试卷学年 第 1学期 高等数学 课程试卷( B 卷)本试卷共 9 页；考试时间 120分钟；任课教师 课程组课程组课程组 ；出卷时间年学院学院 专业专业 2009 年级年级 班学号学号 姓名姓名 得分一、填空题一、填空题((每小题3分,共15分) 评分阅卷人1、已知22(,)yf x y x y x +=-,则=),(y x f _____________2、已知p =ò¥+¥--dx ex 2,则=ò¥+--dx e x x0 21___________.3、函数22(,)1f x y x xy y y =++-+在__________点取得极值4、已知y y x x y x f arctan )arctan (),(++=,则=¢)0,1(xf ________.5、以xe x C C y 321)(+=(21,C C 为任意常数)为通解的微分方程是为通解的微分方程是____________________.评分阅卷人p ï222231x y dxdy --2231x y dxdy --2231x y dxdy --三、计算题三、计算题((每小题6分,共60分)评分11、求由23x y =,4=x ,0=y 所围图形绕y 轴旋转的旋转体的体积转体的体积. .12、求二重极限、求二重极限 11lim22220-+++®®y x y x y x .评分评阅人评分评阅人y x 评分评阅评分评阅人ò 评分评阅评分评阅人)1133-+n n 评分评阅人评分评阅人评分评阅人评分评阅人评分x y 评分评阅人评分评阅人一、填空题一、填空题((每小题3分,共15分)1、2(1)1x y y -+. 2、p . 3、)32,31(-. 4、1. 5、"6'0y y y -+=. 二、选择题二、选择题((每小题3分,共15分)6、(C ). .7、 (B).8、(A ) .9、(D). 10、(D).三、计算题三、计算题((每小题6分,共60分)11、求由23x y =,4=x ,0=y 所围图形绕y 轴旋转的旋转体的体积轴旋转的旋转体的体积. . 解：32yx =的反函数为23,0x y y =>。

南京信息工程大学试卷答案及评分标准2018 －2019学年 第 2 学期 线性代数 课程试卷( B 卷)一、填空题 (每小题3分，共15分)1. 设A 是n 阶方阵，且0A =≠a ，*A 是A 的伴随矩阵，则*A = . 答案：1-n a .2. 20192018010123001100456010001789100⎛⎫⎛⎫⎛⎫⎪ ⎪⎪= ⎪ ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.答案：456123789⎛⎫ ⎪⎪ ⎪⎝⎭.3.设101112011A ⎛⎫⎪= ⎪ ⎪⎝⎭，123αα,,α为线性无关的3维列向量组，则向量组123A αA αA ,,α的秩为 . 答案：2.4. 设矩阵10000101a A ⎛⎫ ⎪= ⎪ ⎪⎝⎭与矩阵100010001Λ⎛⎫⎪= ⎪ ⎪-⎝⎭相似，则a = .答案：0.5. 设二次型1234()f x x x x ,,,的秩为3，负惯性指数为1，则1234()f x x x x ,,,的规范形为 . 答案：222123+-y y y .二、选择题 (每小题3分，共15分)1. 设A ,B 是四阶矩阵，且有4A =，1B =，234α,,,,βγγγ均为4维向量，()234A α=,,,γγγ，()234B =,,,βγγγ，则A B +=( C ).(A) 5； (B) 10； (C) 40； (D) 20. 2. 设A 是46⨯矩阵，则齐次线性方程组Ax =0( C ).(A) 无解； (B) 只有零解； (C) 有非零解； (D) 不一定有非零解.3. 设向量组123αα,,,αβ线性相关，向量组234αα,,,αβ线性无关，则( B ). (A) β能由向量组1234αα,,,αα线性表示； (B) 1α能由向量组123αα,,,αβ线性表示； (C) 向量组1234αα,,,αα线性相关； (D) 向量组1234αα,,,αα线性无关. 4. 设A 为3阶矩阵，()123P αα=,,α为可逆矩阵，使得1012P AP -⎛⎫⎪= ⎪ ⎪⎝⎭，则()123A αα++=α( B ).(A) 12αα+; (B) 232α+α; (C) 23α+α; (D) 122αα+. 5. n 阶实对称矩阵A 正定的充要条件是( D ).(A) R()A =n ; (B) A 所有特征值非负; (C) A 的主对角线元素都大于零; (D) 1A -正定.三、计算题 (每小题6分，共18分)1. 设1235342111231211-=-D ，A ij 是D 中元素ij a 的代数余子式，求21222324A A A A +++.解：212223241235111111231211A A A A -+++=- ……………………3分11111111123503240112302121211100--=-=-=--. ………………6分2. 设120340121A ⎛⎫⎪= ⎪ ⎪-⎝⎭，231240B -⎛⎫= ⎪-⎝⎭,求(1)TAB ; (2)4A .解：(1)T 120228634034181012110310AB -⎛⎫⎛⎫⎛⎫⎪⎪ ⎪== ⎪⎪ ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭⎝⎭. ……………………3分(2)12046464340128121A A ===--. ……………………6分3. 设3阶矩阵A 满足2A A E +=，求1A -和()13A E -+.解：矩阵A 满足2A A E +=可得()A A E E +=，故1A A E -=+.………2分矩阵A 满足2A A E +=可得265A A E E +-=-， ………4分分解因式可得：()()325A E A E E +-=-，即()235E A A E E -⎛⎫+= ⎪⎝⎭，故()1235E AA E --+=. ……………………6分 四、求向量组12342111112146223697αααα--⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭，，，的秩及一个极大无关组，并将其余向量用此极大无关组线性表示. (本题满分10分)解：令()123421111121112121114622231136973697A αααα---⎛⎫⎛⎫⎪ ⎪---⎪ ⎪==→ ⎪ ⎪---- ⎪ ⎪--⎝⎭⎝⎭,,, 112111211121022201110111055300020001033400010000---⎛⎫⎛⎫⎛⎫⎪ ⎪⎪---⎪ ⎪ ⎪→→→ ⎪ ⎪ ⎪-- ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭1010011000010000-⎛⎫⎪- ⎪→ ⎪⎪⎝⎭， ……………………6分则向量组1234αααα,,,的秩为3，124ααα,,为该向量组的一个极大无关组， 且312ααα=--. ……………………10分五、设()T 1111,,,是线性方程组123412341234223240+-+=⎧⎪++-=⎨⎪-++=⎩x x x x x x x x x ax x x 的一个解向量，求该线性方程组的通解. (本题满分10分)解：将12341====x x x x 代入方程组可得3=a ， ……………………2分 对增广矩阵作初等行变换()111121111211112213240154001540131100420200981A b ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-→--→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭51410010432994545010010999981810010019999⎛⎫⎛⎫ ⎪⎪-⎪⎪ ⎪⎪→-→-⎪⎪ ⎪⎪ ⎪ ⎪-- ⎪⎝⎭⎝⎭……………………8分 故齐次线性方程组的基础解系为T5481999ξ⎛⎫=- ⎪⎝⎭,,,，所以该线性方程组的通解为()TT 54811111999x ⎛⎫=-+ ⎪⎝⎭k ,,,,,,.……………10分六、已知三阶实对称矩阵A 的三个特征值为12302λλλ===,，且对应于特征值0的特征向量为()T1101α=-,,，求矩阵A .(本题满分10分) 解：设对应于特征值2为的特征向量为()T123x =x x x ,,，因为实对称矩阵不同特征值对应的特征向量是正交的，故[]10x α=,.即130-=x x ，则其基础解系为()T 2101α=,,，()T3010α=,,. ………………4分 令()123110001110P ααα⎛⎫ ⎪== ⎪ ⎪-⎝⎭,,，求得11102211022010P -⎛⎫-⎪ ⎪= ⎪⎪ ⎪⎝⎭，………………8分则1022P AP Λ-⎛⎫ ⎪== ⎪ ⎪⎝⎭， 进而11102211001011100120020221102101010A P ΛP -⎛⎫-⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪=== ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪- ⎪⎝⎭⎝⎭⎝⎭ ⎪⎝⎭.………10分 七、已知二次型21232121323(,,)=3282-+-f x x x x x x x x x x ，(1) 用正交变换x Qy =将此二次型化成标准形，并求出正交矩阵Q ； (2) 说明123(,,)=1f x x x 在几何上表示什么图形. (本题满分12分)解：(1)该二次型的矩阵为014131410A -⎛⎫⎪=-- ⎪ ⎪-⎝⎭，则()()()14131425041A E λλλλλλλ---=---=-+--=--， 故特征值为123425λλλ=-==,,， ………………………4分当14λ=-时，有4141014171010414000A E -⎛⎫⎛⎫ ⎪ ⎪+=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭，对应于14λ=-的一个特征向量为1101p -⎛⎫⎪= ⎪ ⎪⎝⎭.当22λ=时，有2141012111012412000A E ---⎛⎫⎛⎫ ⎪ ⎪-=--→- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭，对应于22λ=的一个特征向量为2121p ⎛⎫⎪= ⎪ ⎪⎝⎭.当35λ=时，有2141015111011412000A E ---⎛⎫⎛⎫ ⎪ ⎪-=--→ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭，对应于35λ=的一个特征向量为3111p ⎛⎫⎪=- ⎪ ⎪⎝⎭. ………………………7分由于123p p p ,,两两正交，故只需对它们单位化.令111101p e p -⎛⎫⎪==⎪⎪⎭，222121p e p ⎛⎫⎪==⎪⎪⎭，333111p e p ⎛⎫⎪==-⎪⎪⎭，则正交矩阵0Q ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭. 且在正交变换x Qy =下，二次型可化成标准形222123123(,,)=425-++f y y y y y y . ………………………10分(2) 222123=425=1-++f y y y 表示单叶双曲面. ………………………12分 八、设向量组123ααα,,线性无关，且1123βααα=--,2123βααα=+-,3123βααα=-+.试证明向量组123βββ,,线性无关.(本题满分10分) 解：假设存在数123,,k k k 使得1122330βββ++=k k k ，则有 ()()()1231123212330ααα+++-+-+--+=k k k k k k k k k , ……………4分 因为向量组123ααα,,线性无关，所以123123123 000++=⎧⎪-+-=⎨⎪--+=⎩k k k k k k k k k ，解得: 1230===k k k , ……………8分因此向量组123βββ,,线性无关. ……………10分 注：有的题目有多种解法，以上解答和评分仅供参考。

南京信息工程大学线性代数（32学时）课程试卷（B ）本试卷共 2 页；考试时间 120 分钟；出卷时间 2012 年 6 月系 级 专业学号 姓名一、选择题（每小题 3 分，共 15分）：1．设A 为n 阶方阵，1>n ，若λ为实数，则有（ ）（A ）A A =λ （B ）A A λλ= （C ）A A n λλ= （D ）n n A A λλ=2．设A 、B 均为n 矩阵()2≥n ，则必有( )(A) B A B A +=+ (B) BA AB =（C ）A 、B 都不可逆 (D) ()111---+=+A B B A 3．下列向量组中，能作为3R 基的是 ( )(A) (1,0,0,0),(0,1,0,0),(0,0,1,0)T T T (B) (1,0,0),(0,1,0)T T(C) (1,0,0),(1,1,0),(1,1,1)T T T (D) (1,2,3),(0,1,1),(0,2,2)T T T 4.若⎪⎪⎪⎭⎫ ⎝⎛+=132121111λA 的秩为2，则=λ( ) (A)0 (B)2 (C)-1 (D)15. 设A 为n 阶方阵，且()1-=n A R ,21,αα是b Ax =的两个不同的解向量，则0=Ax 的通解为 ( )(A)1αK (B) )(21αα-K (C))(21αα+K (D) 2αK二、填空题(每小题 3 分，共 15分)：1.设A 为3阶矩阵，且2=A ，则_____=T AA . 2. 若E A A =+232，则1-A = .3. 已知3阶方阵A 的三个特征值为1,-2,3.则1-A 的特征值为 .4．若A 是正交矩阵，则=A .5．向量α线性无关的充要条件 .三、计算下列各式（每小题6分，共12分） (1) x x xx++++1111111111111111； （2）4521011*********-- . 四、设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=300041013A ，判断A 是否可逆，若可逆，求1-A （10分）。

一、 填空题 (每小题 3 分，共 15 分)1、 设向量()()2,3,4,1,1,0TTa b ==-，则a 与b 的内积[],a b =.2、 计算行列式222111D xy z x y z ==.3、 设A 为三阶方阵，且1=3A ，则()1*43=A A -- .4、 3阶矩阵A 有特征值1,2,3-，则2A A *+= . 5、 设A 为n 阶方阵，且()1R A n =-,则A = . 二、 选择题 (每小题 3分，共 15 分)1、设A ,B 均为n 阶可逆矩阵，以下等式正确的是( ) (A)()()22A B A B A B +-=-；(B)()111A B A B ---+=+；(C)()2222A B A AB B +=++；(D)()AB B A ***=.2、设A 是3阶矩阵，将A 的第1列与第2列互换得到B ,再把B 的第2列加到第3列得到C ,则满足AQ C =的可逆矩阵Q 为( )(A) 010100101⎛⎫ ⎪ ⎪ ⎪⎝⎭； (B) 010101001⎛⎫ ⎪ ⎪ ⎪⎝⎭；(C) 010100011⎛⎫⎪⎪ ⎪⎝⎭； (D)011100001⎛⎫⎪ ⎪ ⎪⎝⎭. 3、设向量组123,,ααα线性无关，向量1β可由123,,ααα线性表示，向量2β不能由123,,ααα线性表示，则必有( )(A) 121,,ααβ线性无关； (B) 122,,ααβ线性无关；(C) 2312,,,ααββ线性相关； (D) 12312,,,αααββ+线性相关.4、A ,B 是n 阶矩阵，且A B 、相似,则( )(A)A ,B 的特征矩阵相同；(B)A ,B 相似于同一个对角阵；(C)A ,B 的特征方程相同； (D)存在正交阵Q ,使得1T Q AQ Q AQ B -==.5、设A 是n 阶方阵，且()1R A n =-，12,αα是Ax b =的两个不同的解向量，则0Ax =的通解为( )(A) 1k α； (B) ()12k αα-； (C)()12k αα+； (D) 2k α.三、计算题(每小题6分，共18分)1、设行列式2117111212357914D =--, 求41424344A A A A +++.2、已知3400430000200022A ⎛⎫⎪-⎪= ⎪⎪⎝⎭， 求8A . 3、设二次型()11221223,350x f x x x x x -=-，求此二次型对应的矩阵.四、设矩阵300011014⎛⎫⎪=- ⎪ ⎪⎝⎭A ，361123⎛⎫ ⎪= ⎪ ⎪-⎝⎭B ，且满足2AX X B =+，求矩阵X . (本题10分)五、求非齐次线性方程组的123123123222121x x x x x x x x x -++=-⎧⎪-+=⎨⎪+-=⎩的通解. (本题10分)六、设向量组()11,1,0Tα=，()21,0,1Tα=-，()30,1,1T α=，()41,1,Tk α=的秩为2，(1)求k ；(2)求此向量组的一个极大线性无关组，并把其余向量用该极大线性无关组线性表示.(本题10分)七、设η为线性方程组()0AX b b =≠的一个解，12,,n r ξξξ-为对应齐次线性方程组0AX =的基础解系，证明：12,,,n r ξξξη-线性无关. (本题10分)八、设二次型()222123123121323,,2282f x x x x x ax x x x x x x =-++-+的秩为2.(1)求a 的值；(2)求正交变换x Qy =，把()123,,f x x x 化成标准形.(本题12分)。

2013南信大考研数学一、填空题(每小题5分，共25分)1、lim x→0(cos √x)1x= 。

2、设{x =tan −1t y =ln (1+t 2)，则ð2y ðx 2= 。

3、设L 是圆周x 2+y 2=4按逆时针方向，则∮(2xye x −y )dx +2(x −L 1)e x dy = 。

4、微分方程y ′′−4y ′+4y =xe x 的通解为 。

5、∫(1+x 3)(e x +e −x )dx 1−1= 。

二、选择题(每小题5分，共25分)1、已知连续函数f(x)在x=0处可导，且lim x→0f(x)2x−sin x =1，则f ′(0)=( )。

(A) 1； (B) 0； (C) -1； (D) 2。

2、设L 是圆周x 2+y 2=1，则∮(x 2+y 2+2x )ds =L( )。

(A) −2π； (B) 2π； (C) 2√2π； (D) 2π2。

3、二重积分∫dθπ20∫f(r cos θ,r sin θ)rdr cos θ0可写成( )。

(A) ∫dy 10∫f(x,y)dx √y−y 20； (B) ∫dy 10∫f(x,y)dx √1−y 20；(C) ∫dx 10∫f(x,y)dy 10； (D) ∫dx 10∫f(x,y)dy √x−x 20。

4、设函数y =f(x)是微分方程y ′′−2y ′+4y =0的一个解，若f (x 0)>0，f ,(x 0)=0，则函数f(x)在点x 0( )。

(A) 取到极大值； (B) 取到极小值；(C) 某个邻域内单调增加； (D) 某个邻域内单调减小。

5、设y =y(x)由方程e x+y −cos (xy )=e −1确定，则y =y(x)在点(0,1)处切线方程( )(A) x +y −1=0；(B) x −y −1=0；(C) −x +y −1=0 (D) x +y +1=0。

三、(本题10分)设函数z=f(xy,yg(x))，其中f具有二阶连续导数，g(x)可导，且g(1)=1为g(x)的极值，求ð2zðxðy|(1,1)。