《信息论与编码》实验讲义新1
- 格式:doc
- 大小:2.23 MB
- 文档页数:7


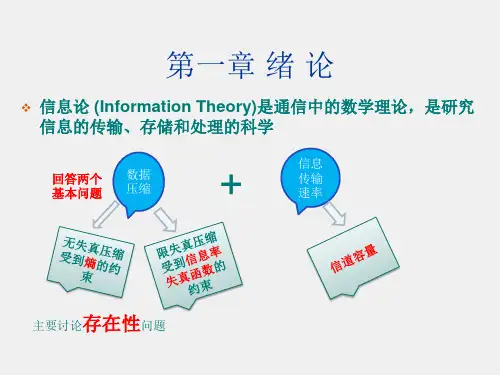
信息论与编码技术实验教案第一章:信息论基础1.1 信息的概念与度量介绍信息的基本概念,信息源的随机性,信息的不确定性。
讲解信息的度量方法,如香农熵、相对熵等。
1.2 信道模型与容量介绍信道的概念,信道的传输特性,信道的噪声模型。
讲解信道的容量及其计算方法,如单符号信道、多符号信道等。
第二章:信源编码与压缩2.1 信源编码的基本概念介绍信源编码的定义、目的和方法。
讲解信源编码的基本原理,如冗余度、平均冗余度等。
2.2 压缩算法与性能评价介绍无损压缩算法,如霍夫曼编码、算术编码等。
讲解有损压缩算法,如JPEG、MP3等。
分析各种压缩算法的性能评价指标,如压缩比、重建误差等。
第三章:信道编码与错误控制3.1 信道编码的基本概念介绍信道编码的定义、目的和方法。
讲解信道编码的基本原理,如纠错码、检错码等。
3.2 常见信道编码技术介绍常用的信道编码技术,如卷积码、汉明码、奇偶校验等。
分析各种信道编码技术的性能,如误码率、编码效率等。
第四章:数字基带传输4.1 数字基带信号与基带传输介绍数字基带信号的概念,数字基带信号的传输特性。
讲解数字基带信号的传输方法,如无编码调制、编码调制等。
4.2 基带传输系统的性能分析分析基带传输系统的性能指标,如误码率、传输速率等。
讲解基带传输系统的优化方法,如滤波器设计、信号调制等。
第五章:信号检测与接收5.1 信号检测的基本概念介绍信号检测的定义、目的和方法。
讲解信号检测的基本原理,如最大后验概率准则、贝叶斯准则等。
5.2 信号接收与性能分析分析信号接收的方法,如同步接收、异步接收等。
讲解信号接收性能的评价指标,如信噪比、误码率等。
第六章:卷积编码与Viterbi算法6.1 卷积编码的基本原理介绍卷积编码的定义、结构及其多项式。
讲解卷积编码的编码过程,包括初始状态、状态转移和输出计算。
6.2 Viterbi算法及其应用介绍Viterbi算法的原理,算法的基本步骤和性能。
讲解Viterbi算法在卷积编码解码中的应用,包括路径度量和状态估计。


信息论与编码技术实验教案第一章:信息论基础1.1 实验目的1. 了解信息的基本概念及其度量方法;2. 掌握信息的熵、冗余度和信道容量等基本概念。
1.2 实验原理1. 信息的基本概念:信息、消息、信源等;2. 信息的度量:平均信息量、熵、冗余度等;3. 信道容量和编码定理。
1.3 实验设备与材料1. 计算机及投影仪;2. 相关实验软件。
1.4 实验步骤1. 讲解信息的基本概念及其度量方法;2. 分析实际例子,演示信息的熵、冗余度和信道容量的计算过程;3. 让学生通过实验软件进行相关计算和分析。
1.5 思考与讨论1. 信息量与消息长度的关系;2. 信道容量在实际通信系统中的应用。
第二章:数字基带编码2.1 实验目的1. 掌握数字基带编码的基本原理;2. 学会使用相关软件进行数字基带编码的仿真。
2.2 实验原理1. 数字基带编码的定义和分类;2. 常用数字基带编码方法:NRZ、RZ、曼彻斯特编码等;3. 数字基带编码的性能评估:误码率、带宽利用率等。
2.3 实验设备与材料1. 计算机及投影仪;2. 相关实验软件。
2.4 实验步骤1. 讲解数字基带编码的基本原理和方法;2. 演示常用数字基带编码的仿真效果;3. 让学生通过实验软件进行数字基带编码的仿真实验。
2.5 思考与讨论1. 数字基带编码的优缺点;2. 如何在实际通信系统中选择合适的基带编码方法。
第三章:信道编码与误码控制3.1 实验目的1. 了解信道编码的基本原理;2. 掌握常见的信道编码方法;3. 学会使用相关软件进行信道编码的仿真。
3.2 实验原理1. 信道编码的定义和作用;2. 常用信道编码方法:卷积编码、汉明编码、里德-所罗门编码等;3. 误码控制原理:检错、纠错等。
3.3 实验设备与材料1. 计算机及投影仪;2. 相关实验软件。
3.4 实验步骤1. 讲解信道编码的基本原理和方法;2. 演示常用信道编码的仿真效果;3. 让学生通过实验软件进行信道编码的仿真实验。



《信息论与编码技术》实验教案第一章:信息论基础1.1 信息的概念与度量介绍信息的基本概念,理解信息的含义学习信息熵的计算方法,掌握信息熵在通信系统中的应用1.2 信源与信道模型学习信源的数学模型,理解信源的随机性和统计特性学习信道的数学模型,了解信道的传输特性第二章:信源编码2.1 信源编码的基本概念理解信源编码的目的和意义学习信源编码的基本原理和方法2.2 常用信源编码技术学习霍夫曼编码、算术编码等常用信源编码技术掌握编码算法的实现和应用第三章:信道编码3.1 信道编码的基本概念理解信道编码的目的和意义学习信道编码的基本原理和方法3.2 常用信道编码技术学习卷积编码、汉明编码等常用信道编码技术掌握编码算法的实现和应用第四章:误码控制与编码技术4.1 误码产生的原因与类型了解通信系统中误码的产生原因和类型学习误码的检测与纠正方法4.2 错误控制编码技术学习自动重传请求(ARQ)、前向纠错(FEC)等错误控制编码技术掌握编码算法的实现和应用第五章:信息加密与安全5.1 信息加密的基本概念理解信息加密的目的和意义学习信息加密的基本原理和方法5.2 常用加密技术学习对称加密、非对称加密等常用加密技术掌握加密算法的实现和应用第六章:数据压缩技术6.1 数据压缩的基本概念理解数据压缩的目的和意义学习数据压缩的基本原理和方法6.2 常用数据压缩技术学习霍夫曼编码、LZ77、LZ78等常用数据压缩技术掌握压缩算法的实现和应用第七章:数字信号传输7.1 数字信号传输的基本概念理解数字信号传输的目的和意义学习数字信号传输的基本原理和方法7.2 数字信号传输技术学习基带传输、频带传输等数字信号传输技术掌握传输算法的实现和应用第八章:调制与解调技术8.1 调制与解调的基本概念理解调制与解调的目的和意义学习调制与解调的基本原理和方法8.2 常用调制与解调技术学习幅度调制、频率调制、相位调制等常用调制技术掌握调制与解调算法的实现和应用第九章:无线通信与编码技术9.1 无线通信的基本概念理解无线通信的目的和意义学习无线通信的基本原理和方法9.2 无线通信编码技术学习扩频技术、多址技术等无线通信编码技术掌握编码算法的实现和应用强调实验的重要性和在实际应用中的作用10.2 拓展学习推荐相关的学习材料和参考书籍鼓励学生探索新技术和发展趋势,提高学生的学习兴趣和动力重点和难点解析重点环节一:信息的概念与度量信息熵的计算方法是理解信息论的核心,需要重点掌握。


信息论与编码实验指导书1 课程实验目的本课程是一门实践性很强的专业课和核心课程,根据课程理论教学的需要安排了6学时的配套实验教学,主要内容涉及信息度量的计算方法、典型信源编码方法、典型信道容量计算方法和数据压缩方法四个实验,这四个实验的开设一方面有助于学生消化、巩固课程理论教学的知识,另一方面又可培养学生实践动手能力,同时为后续课程做好准备。
2 课程实验要求2.1 课程实验准备要求(1)课程实验主要为设计性实验,要求学生熟悉掌握在VC环境下编写和调试C++程序的方法。
(2)要求学生在实验前复习实验所用到的预备知识。
可以查阅教材或者相关的参考资料,这需要学生有自主的学习意识和整理知识的能力。
(3)根据实验项目,设计相关的数据结构和算法,再转换为对应的书面程序,并进行静态检查,尽量减少语法错误和逻辑错误。
上机前的充分准备能高效利用机时,在有限的时间内完成更多的实验内容。
2.2 课程实验过程要求(1)生成源代码。
将课前编写好的书面代码,利用VC自带的编辑器尽快输入为转换为源代码;(2)程序调试和软件测试。
要求学生熟练掌握调试工具,调试正确后,认真整理源程序和注释,给出带有完整注释且格式良好的源程序清单和结果。
(3)完成实验报告。
根据实验内容和完成情况,按照附件1给定的格式完成课程实验报告的编写。
2.3 课程实验报告要求在每次课程实验后要及时进行总结和整理,并编写课程实验报告。
报告格式按江西蓝天学院实验报告纸格式填写。
实验一二维随机变量信息熵的计算[实验目的]掌握二变量多种信息量的计算方法。
[实验学时]2学时[实验准备]1.熟悉二变量多种信息量的计算方法,设计实验的数据结构和算法;2.编写计算二维随机变量信息量的书面程序代码。
[实验内容及步骤]离散二维随机变换熵的计算说明:(1)利用random函数和归一化方法构造一个二维离散随机变量(X,Y);(2)分别计算X与Y的熵、联合熵、条件熵:H(X)、H(Y)、H(X,Y)H(X|Y)、I(X|Y);(3)对测试通过的程序进行规范和优化;(4)编写本次实验的实验报告。

《信息论与编码技术》实验教案一、实验目的1. 理解信息论基本概念,如信息量、信道容量等。
2. 掌握编码技术的基本原理,如Hamming 编码、卷积编码等。
3. 学会使用仿真工具进行信息论与编码技术的实验。
二、实验原理1. 信息论基本概念:信息量、信道容量、误码率等。
2. 编码技术原理:Hamming 编码、卷积编码、解码算法等。
3. 仿真工具的使用:调用相关函数,设置参数,观察实验结果。
三、实验内容1. 实验一:信息量计算与信道容量分析利用仿真工具随机比特序列,计算信息量。
改变信道参数,分析信道容量变化。
2. 实验二:Hamming 编码与解码编写Hamming 编码器和解码器,进行编码和解码操作。
分析误码率与编码位数的关系。
3. 实验三:卷积编码与解码编写卷积编码器和解码器,进行编码和解码操作。
分析误码率与卷积编码器参数的关系。
4. 实验四:不同编码方案性能比较分别使用Hamming 编码和卷积编码对相同长度比特序列进行编码。
比较两种编码方案的误码率和信息传输效率。
5. 实验五:信息论与编码技术在实际应用中的案例分析分析数字通信系统中信息论与编码技术的应用。
了解信息论与编码技术在无线通信、图像传输等领域的应用。
四、实验步骤1. 实验一:信息量计算与信道容量分析随机比特序列,计算信息量。
设置信道参数,观察信道容量变化。
2. 实验二:Hamming 编码与解码编写Hamming 编码器和解码器,进行编码和解码操作。
改变编码位数,分析误码率变化。
3. 实验三:卷积编码与解码编写卷积编码器和解码器,进行编码和解码操作。
改变卷积编码器参数,分析误码率变化。
4. 实验四:不同编码方案性能比较使用Hamming 编码和卷积编码对相同长度比特序列进行编码。
比较两种编码方案的误码率和信息传输效率。
5. 实验五:信息论与编码技术在实际应用中的案例分析分析数字通信系统中信息论与编码技术的应用案例。
了解信息论与编码技术在无线通信、图像传输等领域的应用。
信息论与编码实验报告实验课程名称:赫夫曼编码(二进制与三进制编码)专业信息与计算科学班级信息与计算科学1班学生姓名李林钟学号 *************指导老师王老师(3).算法基本步骤描述(4).编码及注解(见附页1) (5).验证截图:得到信源得出信源序列个得出信源序列的计算信源符输输输输输信源符号的赫弗曼码方编码效平均码输编码效率为:(3.3)(4).验证结果截图:() 2.5595.2%2.68H X R η===附页1:#include<stdio.h>#include<string.h>#include<math.h>#define MAX 100//定义全局变量h存放信息熵double h=0;//定义结构体用于存放信源符号,数目及概率typedef struct{//不同的字符char SOURCECODE;//不同字符出现的次数int NUM;//不同字符出现的概率double PROBABILITY;//赫夫曼编码符号int Code[MAX];int start;//赫夫曼树的父结点int parent;//赫夫曼树的左右子结点int lchild;int rchild;//赫夫曼编码的长度int lengthofhuffmancode;}Hcode;Hcode INFORMATION[MAX];//该函数用来求信源所包含的符号,以及不同符号出现的次数和概率int Pofeachsource(char informationsource[MAX],int a){int i,j=1,m,flag=0;char temp;//预先存入第一个字符,便于与后面的字符进行比较//统计不同的字符存入结构体数组中//利用flag标签来标记每个字符是否出现过,若出现过标记为1,否则置为零INFORMATION[0].SOURCECODE=informationsource[0];for(i=1;i<a;i++){ for(m=0;m<i;m++){flag=0;if(informationsource[m]==informationsource[i]){flag=1;break;}}if(flag==1)continue;elseINFORMATION[j++].SOURCECODE=informationsource[i];}INFORMATION[j].SOURCECODE='\0';printf("信源符号数为:%d\n",j);//统计相同的字符出现的次数//每做一个字符出现次数的统计都将结构体数组里的NUM置为零for(i=0;i<j;i++){ INFORMATION[i].NUM=0;for(m=0;m<a;m++)if(informationsource[m]==INFORMATION[i].SOURCECODE)INFORMATION[i].NUM++;}//统计每个字符出现的概率for(i=0;i<j;i++) INFORMATION[i].PROBABILITY=(float)INFORMATION[i].NUM/a;//将每个不同字符出现的次数概率都显示出来for(i=0;i<j;i++)printf("The NUM and PROBABILITY of Code'%c'is %dand %.3f\n",INFORMATION[i].SOURCECODE,INFORMATION[i].NUM,INFORMATION[ i].PROBABILITY);return j;}//求信源符号的熵void H(int a){int i;for(i=0;i<a;i++){h+=((-1)*(INFORMATION[i].PROBABILITY)*(log(INFORMATION[i].PROBABI LITY)/log(2)));}}//赫夫曼编码函数void Huffman(int a){Hcode cd;int i,j,m=0,lm=0,p,c;double min,lmin;//顺序初始化每个信源父子结点为-1for(i=0;i<a;i++){INFORMATION[i].parent=-1;INFORMATION[i].lchild=-1;INFORMATION[i].lchild=-1;}//循环构造Huffman树for(i=0;i<a-1;i++){//min,lmin中存放两个无父结点且结点权值最小的两个结点min=lmin=MAX;//找出所有结点中权值最小、无父结点的两个结点,并合并之为一颗二叉树for (j=0;j<a+i;j++){if((INFORMATION[j].PROBABILITY<min)&&(INFORMATION[j].parent==-1)){lmin=min;lm=m;min=INFORMATION[j].PROBABILITY;m=j;}else if((INFORMATION[j].PROBABILITY<lmin)&&(INFORMATION[j].parent==-1)){lmin=INFORMATION[j].PROBABILITY;lm=j;}}//设置找到的两个子结点 m、lm 的父结点信息INFORMATION[m].parent=a+i;INFORMATION[lm].parent=a+i;INFORMATION[a+i].PROBABILITY=INFORMATION[m].PROBABILITY+INFORMATION[l m].PROBABILITY;INFORMATION[a+i].parent=-1;INFORMATION[a+i].lchild=m;INFORMATION[a+i].rchild=lm;}for (i=0;i<a;i++){cd.start=a-1;c=i;p=INFORMATION[c].parent;while(p!=-1) /* 父结点存在 */{if(INFORMATION[p].lchild==c)cd.Code[cd.start]=1;elsecd.Code[cd.start]=0;cd.start--; /* 求编码的低一位 */c=p;p=INFORMATION[c].parent; /* 设置下一循环条件 */ }//保存求出的每个叶结点的赫夫曼编码和编码的起始位for(j=cd.start+1;j<m;j++){ INFORMATION[i].Code[j]=cd.Code[j];}INFORMATION[i].start=cd.start;}}main(){//定义存放信源符号的数组char informationsource[MAX];int i,j,m;double averageofhuffmancode=0.0,Eita,cV=0.0;printf("please input the source of information:");for(i=0;;i++){scanf("%c",&informationsource[i]);if(informationsource[i]=='\n')break;}informationsource[i]='\0';printf("信源序列为:");//显示已输入的一串信源符号puts(informationsource);//返回不同信源符号的数目m=Pofeachsource(informationsource,i);//求信源的符号熵H(m);printf("信源的符号熵:H(X)=%.3f(比特/符号)\n",h);Huffman(m);//输出已保存好的所有存在编码的赫夫曼编码for(i=0;i<m;i++){printf("%c's Huffman code is: ",INFORMATION[i].SOURCECODE); for(j=INFORMATION[i].start+1;j<m;j++)printf("%d",INFORMATION[i].Code[j]);INFORMATION[i].lengthofhuffmancode=m-INFORMATION[i].start-1; printf("\n");}//求赫夫曼编码的平均码长和编码效率for(i=0;i<m;i++)averageofhuffmancode+=INFORMATION[i].PROBABILITY*INFORMATION[i].l engthofhuffmancode;printf("赫夫曼编码的平均码长为:%lf(码元/信源符号)\n",averageofhuffmancode);Eita=h/averageofhuffmancode;printf("赫夫曼编码的编码效率为:%lf\n",Eita);//求赫弗曼编码的码方差for(i=0;i<m;i++)cV+=INFORMATION[i].PROBABILITY*INFORMATION[i].lengthofhuffmancode *INFORMATION[i].lengthofhuffmancode;cV-=averageofhuffmancode*averageofhuffmancode;printf("赫弗曼编码的码方差为:%lf\n",cV);}附页2#include <iostream.h>#include <math.h>#include <string.h>#include <stdio.h>#include <stdlib.h>#include <vector> //为了使用vector容器using namespace std; ///vector属于std命名域,因此使用全局命名域方式struct Huffman_InformationSource //信源类型{char InformationSign[10]; //信源符号double Probability; //概率char Code[10]; //编码结果int CodeLength; //码长};struct HuffNode //赫夫曼树的节点类型{char InformationSign[10];double Probability;HuffNode *LeftSubtree,*middleSubtree,*RightSubtree,*Next;char Code[10];int CodeLength;};class CHuffman_3 //三进制赫夫曼编码{public:CHuffman_3() //初始化{ISNumber=0;AvageCodeLength=0.0;InformationRate=0.0;CodeEfficiency=0.0;}~CHuffman_3(){DestroyBTree(HuffTree);}void Huffman_Input(); //输入信息void Huffman_Sort(); //排序void Huffman_Tree(); //构造赫夫曼树void Huffman_Coding(); //生成赫夫曼编码void Huffman_CodeAnalyzing(); //结果分析void Huffman_Display(); //显示结果信息void DestroyBTree(HuffNode *TreePointer); //释放资源private:vector<Huffman_InformationSource>ISarray; //声明ISarray数组,初始时为空int ISNumber; //符号个数double AvageCodeLength; //平均码长double InformationRate; //信息率double CodeEfficiency; //编码效率HuffNode * HuffTree; //赫夫曼树private:void Huffman_Code(HuffNode *TreePointer);};//输入信源信息如果需要添加信源信息在这里修改即可void CHuffman_3::Huffman_Input(){Huffman_InformationSource temp1={"A",0.40,"",0};ISarray.push_back(temp1);Huffman_InformationSource temp2={"B",0.18,"",0};ISarray.push_back(temp2);Huffman_InformationSource temp3={"C",0.10,"",0};ISarray.push_back(temp3);Huffman_InformationSource temp4={"D",0.10,"",0};ISarray.push_back(temp4);Huffman_InformationSource temp5={"E",0.07,"",0};ISarray.push_back(temp5);Huffman_InformationSource temp6={"F",0.06,"",0};ISarray.push_back(temp6);Huffman_InformationSource temp7={"G",0.05,"",0};ISarray.push_back(temp7);Huffman_InformationSource temp8={"H",0.04,"",0};ISarray.push_back(temp8);ISNumber=ISarray.size();}//按概率“从大到小”排序:void CHuffman_3::Huffman_Sort(){Huffman_InformationSource temp;int i,j;for(i=0;i<ISNumber-1;i++)for(j=i+1;j<ISNumber;j++)if(ISarray[i].Probability<ISarray[j].Probability){temp=ISarray[i];ISarray[i]=ISarray[j];ISarray[j]=temp;}}//基于ISarray数组构造赫夫曼树void CHuffman_3::Huffman_Tree(){int i;HuffNode *ptr1,*ptr2,*ptr3,*ptr4,*temp1,*temp2;//(1):基于数组,创建单向链表ptr1=new HuffNode;strcpy(ptr1->InformationSign,ISarray[0].InformationSign);ptr1->Probability=ISarray[0].Probability;strcpy(ptr1->Code,ISarray[0].Code);ptr1->LeftSubtree=NULL;ptr1->middleSubtree =NULL;ptr1->RightSubtree=NULL;ptr1->Next=NULL;HuffTree=ptr1; //赋给数据成员HuffTree for(i=1;i<ISNumber;i++){ptr2=new HuffNode;strcpy(ptr2->InformationSign,ISarray[i].InformationSign);ptr2->Probability=ISarray[i].Probability;strcpy(ptr2->Code,ISarray[i].Code);ptr2->LeftSubtree=NULL;ptr2->middleSubtree =NULL;ptr2->RightSubtree=NULL;ptr2->Next=ptr1;ptr1=ptr2;}//结果:链表的表头为数组的最小元素。
信息论与编码实验讲义李敏编写乐山师范学院物电学院二零一零年三月制实验1 绘制二进熵函数曲线一、实验内容用Excel 或Matlab 软件制作二进熵函数曲线。
二、实验环境1. 计算机2. Windows 2000 或以上3. Microsoft Office 2000 或以上4. Matlab 6.0或以上 三、实验目的1. 掌握Excel 的数据填充、公式运算和图表制作2. 掌握Matlab 绘图函数3. 掌握、理解熵函数表达式及其性质 四、实验要求1. 提前预习实验,认真阅读实验原理以及相应的参考书。
2. 认真高效的完成实验,实验中服从实验室管理人员以及实验指导老师的管理。
3. 认真填写实验报告。
五、实验原理1. Excel 的图表功能(略,参考书1中相关章节)2. 信源熵的概念及性质,参考书2中20~28页()()[]()[]())(1)(1 .log )( .)( 1log 1log )(log )()(10 , 110)(21Q H P H Q P H b nX H a p H p p p p x p x p X H p p p x x X P X ii i λλλλ-+≥-+≤=--+-=-=≤≤⎩⎨⎧⎭⎬⎫-===⎥⎦⎤⎢⎣⎡∑六,实验数据P=0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.700.75 0.80 0.85 0.90 0.95 1.00 绘制H (P )—P 函数图 七、参考书1. 《信息技术基础》河北大学出版社2. 《信息论与编码》陈运等,电子工业出版社3. 《Matlab 与科学计算》,电子工业出版社实验2 计算一阶马尔可夫信源的熵一、实验内容利用Matlab 强大的矩阵运算功能计算一阶马尔可夫信源的平稳分布概率,并在Matlab 环境下,编程计算该一阶马尔可夫信源的熵,并绘制熵函数曲线。
信息论与编码实验一离散信源信息量的计算摘要:I.引言- 信息论与编码实验一的主题- 离散信源信息量的计算的重要性II.离散信源的定义- 离散信源的定义- 离散信源的特点III.信息量的计算- 信息量的定义- 离散信源信息量的计算方法- 计算实例IV.信息熵的定义- 信息熵的定义- 信息熵的性质- 计算实例V.编码与解码- 编码的过程- 解码的过程- 编码与解码的实例VI.总结- 离散信源信息量的计算的重要性- 对信息论与编码实验一的回顾正文:I.引言信息论与编码是通信工程中的重要内容,它旨在研究如何在传输过程中有效地传输信息。
在信息论与编码实验一中,我们主要关注离散信源的信息量的计算。
离散信源是我们日常生活中最常见的信源类型,例如文字、声音、图像等。
因此,了解离散信源信息量的计算方法对于理解和应用信息论与编码理论具有重要意义。
II.离散信源的定义离散信源是指信息以离散的方式存在的信源。
离散信源的特点是信息符号是离散的、不连续的,且每个符号的出现是相互独立的。
离散信源可以分为无记忆离散信源和有记忆离散信源。
无记忆离散信源是指信源发出的每个符号的概率分布与过去符号无关,而有记忆离散信源则与过去符号有关。
III.信息量的计算信息量是衡量信息的一个重要指标,它表示了接收者在接收到符号后所获得的信息。
对于离散信源,信息量的计算公式为:I(X) = -∑P(x) * log2(P(x)),其中X 表示离散信源,P(x) 表示符号x 出现的概率。
通过计算信息量,我们可以了解信源的信息程度,从而为后续的编码和解码提供依据。
IV.信息熵的定义信息熵是信息论中的一个重要概念,它表示了信源的平均信息量。
信息熵的定义为:H(X) = -∑P(x) * log2(P(x)),其中X 表示离散信源,P(x) 表示符号x 出现的概率。
信息熵具有以下性质:1)信息熵是信息量的期望;2)信息熵的值是有限的,且在0 到比特数之间;3)当信源的每个符号出现的概率相同时,信息熵最大。
实验一、计算二阶马尔可夫信源的熵
一、实验目的
1.掌握MATLAB 的矩阵运算功能和图表功能。
2.掌握二阶马尔可夫信源熵的求解方法。
二、实验条件
计算机一台,MATLAB 仿真软件。
三、实验内容
(1)MATLAB 的应用(请参阅相关书籍) (2)实验主要内容
已知信源的转移矩阵P ⎡⎢⎢⎢⎢⎣0.80=0.50
0.200.50 00.5
00.2 00.500.8⎤⎥⎥⎥⎥
⎦,
1)利用Matlab 强大的矩阵运算功能计算二阶马尔可夫信源的平稳分布概率。
2) 在Matlab 环境下,编程计算该二阶马尔可夫信源的熵。
(3)实验原理
对于时齐、遍历的马尔可夫链,已知
P 为信源的转移矩阵,p p P p p ⎡⎢⎢⎢⎢
⎣11213141
= p p p p 12223242 p p p p 13233343 p p p p ⎤
⎥⎥⎥
⎥⎦14243444,()j p S 为稳态概率,
()j j p S W =,且W P W ∙=
则信源熵为
1()(/)j
m j j S H H p S H X S ∞+=∑=
其中(/)(/)log (/)j i j i j H X S p x S p x S ∑=-,
如11111121213131414(/)log log log log )H X S p p p p p p p p +++=-(
四、实验要求及分析
(1)进一步熟悉MATLAB 的矩阵运算功能。
(2)按照书上p15页、p34页例题进行理论分析,并与所做实验进行对比。
实验二、绘制二进制熵函数曲线
一、实验目的
1.掌握二进制符号熵的计算;
2.掌握MATLAB的应用;
3.掌握Matlab绘图函数;
4.掌握、理解熵函数表达式及其性质
二、实验条件
计算机一台,MATLAB仿真软件。
三、实验内容
(1)MATLAB的应用(请参阅相关书籍)
(2)打开MATLAB,在命令窗口中输入eidt,弹出编辑窗口,如图1:
图1 MATLAB的编辑窗口
(3)输入源程序:
clear;
x=0.001:0.001:0.999
y=-x.*log2(x)-(1-x).*log2(1-x);
plot(x,y);
grid on
(4)保存文件为entropy.m;
(5)单击Debug菜单下的Run,或直接按F5执行;
(6)执行后的结果图2:
四、实验分析
(1)熵函数是一个严格上凸函数
(2)熵的极大值,二进符号的熵在p(x1)=p(x2)=0.5取得极大值
(3)调调整p(x1)的取值步长,重画该曲线
图2 二进制符号熵函数图
实验三、一般信道容量计算
一、实验目的
1.熟悉工作环境及Matlab 软件 2.理解平均互信息量表达式及其性质 3.理解信道容量的含义
二、 实验原理
1.平均互信息量(I(X;Y))是统计平均意义下的先验不确定性与后验不确定性之差,是互信息量的统计平均
:
()()()()()()
;/;/=-=-I X Y H X H X Y I Y X H Y H Y X
2.离散信道的数学模型
离散信道的数学模型一般如图1所示。
图中输入和输出信号用随机矢量表示,输入信号为X= (X1, X2,…, XN),输出信号为Y= (Y1, Y2,…, YN);每个随机变量Xi 和Yi 又分别取值于符号集A={a1, a2, …, ar}和B={b1, b2, …, bs},其中r 不一定等于s ;条件概率P(y|x) 描述了输入信号和输出信号之间的统计依赖关系,反映了信道的统计特性。
21N 21N
∑=1
)|(x y P
图1离散信道模型
二元对称信道
这是很重要的一种特殊信道(简记为BSC ),。
它的输入符号X 取值于{0,1},输出符号Y 取值于{0,1},r=s=2, a1=b1=0,a2=b2=1,传递概率为
p p P a b P =-==1)0|0()|(11, p p P a b P =-==1)1|1()|(22
p P a b P ==)1|0()|(21, p P a b P ==)0|1()|(12
其中,)0|1(P 表示信道输入符号为0而接收到的符号为1的概率,)1|0(P 表示信道输入符号为1而接受到的符号为0的概率,它们都是单个符号传输发生错误的概率,通常用p 表示。
而)0|0(P 和)1|1(P 是无错误传输的概率,通常用p p =-1表示。
X 1-p Y
01=a 10b =
p
p
12=a 21b =
二元对称信道
用矩阵来表示,即得二元对称信道的传递矩阵为
⎥⎦⎤
-⎢⎣⎡-p p p
p 111100 依此类推,一般离散单符号信道的传递概率可用以下形式的矩阵来表示,即
b1 b2 … bs
⎥
⎥⎥
⎥⎦
⎤⎢
⎢⎢⎢⎣⎡)|()|()|()|()
|()|()|()|()|(212222
11121121
r s r r s s r
a b P a b P a b P a b P a b P a b P a b P a b P a b P a a a
并满足式
∑==s
j
i j a b P 1
1)|( (r i ,,2,1 =)。
为了表述简便,记ij i j p a b P =)|(,信道的传递矩阵表示为
⎥
⎥
⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡=rs r r s s p p p p p p p p p P
1
1
22221
11211
而且满足
0>j i p ⎩⎨⎧是列的标号是行的标号
j i
平均互信息
平均互信息表示接收到输出符号后平均每个符号获得的关于输入变量X 的信
息量,也表示输入与输出两个随机变量之间的统计约束程度。
∑∑-=
XY
X
y x P xy P x P x P Y X I )
|(1
log )()(1log )();(
∑
∑
-=
XY
XY
y x P xy P x P xy P )
|(1log
)()
(1
log )(
∑
=
XY x P y x P xy P )()|(log
)(
∑=
XY
y P x P xy P xy P )()()
(log )(
∑
=
XY y P x y P xy P )
()
|(log
)( 其中X 是输入随机变量,Y 是输出随机变量。
平均互信息是互信息(即接收到输出符号y 后输入符号x 获得的信息量)的统计平均值,所以永远不会取负值。
最差情况是平均互信息为零,也就是在信道输出端接收到输出符号Y 后不获得任何关于输入符号X 的信息量。
对于每一个确定信道,都有一个信源分布,使得信息传输率达到最大值,我们把这个最大值称为该信道的信道容量。
()
max {(;)}
P x C I X Y =
相应的输入概率分布称为最佳输入分布。
三、实验内容
1.绘制平均互信息量图形
对于二元对称信道的输入概率空间为0,1(),1ωωω⎡⎤⎡⎤
=⎢⎥⎢⎥
=-⎣⎦⎣⎦X P x 平均互信息:
根据:1
()()(|)1===∑r
j i j i i P b P a P b a
所以:
(;)()(/)
=-I X Y H Y H Y X 1()()(/)log
(/)
=-∑∑X
Y
H Y P x P y x P y x 11()()[log
log ]=-+∑X
H Y P x p p p p
11
()[log
log ]()()=-+=-H Y p p H Y H p p p
2
1(0)()(0|)(0)(0|0)(1)(0|1)ωω====+=+∑i i i P y P a P a P P P P p p
2
1
(1)()(0|)(0)(1|0)(1)(1|1)ωω====+=+∑i i i P y P a P a P P P P p p
1111
(;)()()()log ()log [log log ]
()()()
ωωωωωωωωωω=-=+++-+++=+-I X Y H Y H p p p p p p p p p p p p p
H p p H p 请绘制当
,ωp 从0到1之间变化时的平均互信息熵曲线
2. 信道容量图形
一个信道是一个二进制输入,二进制输出的信道,输入和输出字母表{0,1}==X Y ,且该信道特性由发送1码和0码的两个错误转移概率(0|1)=P e 和(0|1)0=P 来表征。
绘出当
0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1=e 时的平均互信息(;)I X Y 和(1)==p P X 间的
函数关系。
确定每种情况下的信道容量。
四、实验报告要求
你能从实验图形中了解它的一些什么性质?。