当前位置：文档之家 › 高二数学课件 二项分布

高二数学课件 二项分布

  • 格式：ppt
  • 大小：1.80 MB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

7.4.1二项分布课件-高二下学期数学人教A版选择性必修第三册

7.4.1二项分布课件-高二下学期数学人教A版选择性必修第三册
X
0
1
P
1 p
p
两点散布是一种特殊的二项散布，即是n=1的二项散布；
二项散布可以看做两点散布的一般情势.
例题讲授
例1 将一枚质地均匀的硬币重复抛掷10次，求:
(1) 恰好出现5次正面朝上的概率；
(2) 正面朝上出努利实验是什么？
重复实验的次数是多少？
(2)在伯努利实验中，我们关注什么？在n重伯努利实验中呢？
(1) 伯努利实验做一次实验, n重伯努利实验做n次实验.
(2)在伯努利实验中, 我们关注某个事件A是否产生;
在n重伯努利实验中, 我们关注事件A产生的次数X .
随机
实验
(1)
伯努利
实验
事件A
掷硬币 正面朝上
(2)
射击
(3)
有放回
抽产品
P(A)
5
5
(2) 正面朝上出现的频率在[0.4, 0.6]内等价于4≤X≤6，于是所求概率为
672 21
P (4 X 6) C 0.5 C 0.5 C 0.5

1024 32
4
10
10
5
10
10
6
10
10
归纳总结
随机变量X服从二项散布的三个前提条件：
(1) 每次实验都是在同一条件下进行的；
i =1
D( X ) E ( X 2 ) [ E ( X )]2
性质
( + ) = () +
(，为常数,且 ≠ )
( + ) = ()
(，为常数,且 ≠ )

导入新课
前面我们学习了互斥事件、条件概率、相互独立事件的意义, 这

二项分布课件

二项分布课件

概率与置信水平之间存在一定的关系 。在确定置信区间时，需要考虑到概 率的大小。
概率计算公式
根据二项分布的定义，可以使用概率 计算公式来计算某一事件发生的概率 。公式包括成功的次数和试验次数等 参数。
置信区间的确定
置信区间的概念
置信区间是指在一定置信水平下，某一参数可能取值的一个范围。 在二项分布中，置信区间通常用于估计成功概率的区间范围。
03
记录每次试验的结果， 并计算成功次数和概率 。
04
可使用图形化工具（如 matplotlib）绘制理论 概率与模拟结果的对比 图。
利用R语言进行二项分布模拟实验
安装并打开R语言环境。
使用循环结构模拟多次试 验，并记录每次试验的成 功次数。
使用“runif()”函数生成 随机数作为试验结果（成 功或失败）。
决策树分析的例子包括：项目管理、资源分配、市场营销等。在这些场景中，二 项分布可以用来计算在不同情况下发生特定事件的概率，从而帮助决策者制定更 有效的计划和策略。
二项分布的模拟实
06
验
利用Excel进行二项分布模拟实验
打开Excel软件，选择一个工作表。
在第一列输入试验次数，在第二列输 入每次试验成功的概率。
样本量计算公式
根据二项分布的性质，可以通过计算公式来确定样本数量 。公式通常基于预期的置信区间、置信水平和误差率等因 素。
样本量与置信水平的关系
样本数量与置信水平之间存在一定的关系。通常，要达到 一定的置信水平，需要足够的样本数量来支持。
概率计算
基本概念
概率与置信水平的关系
在二项分布中，概率是指某一事件发 生的可能性。在统计学中，概率通常 用小数或百分比表示。
二项分布课件(上课)

二项分布教学课件ppt

二项分布教学课件ppt

0.4
0.3
0.2
0.1
0.0
0
1
2
3
x
(0.2+0.8)3 二项分布示意图
构成成-败型实验序列的n次实验中，事件A出现 的次数X的概率分布为：
P X CnX X 1 nX
其中X=0，1，2…，n。 n，π是二项分布的两个参数 。
对于任何二项分布，总有
中国福利彩票
发行量1500万元，特等奖100个，金额5万元； 每张彩票面值2元，中奖概率1/75000。
投入金额 未中概率 中奖概率
100元 1000元 1万元 10万元 100万元 0.99933 0.99336 0.93551 0.51341 0.00127 0.00067 0.00664 0.06449 0.48659 0.99873
例4-2 临床上用针灸治疗某型头疼，有效的概率为60% 现以该疗法治疗3例，其中2例有效的概率是多大？
B(X;n,π)或B(n,π)。
二项分布的概率函数
• 任意一次试验中，只有事件A发生和不发生
两种结果，发生的概率分别是: 和1－
• 若在相同的条件下，进行n次独立重复试验，
用X表示这n次试验中事件A发生的次数，那 么X服从二项分布，记做 XB(n,) 或 B(X;n,π) 。
举例 设实验白鼠共3只，要求它们同种属、同 性别、体重相近，且他们有相同的死亡概率， 即事件“白鼠用药后死亡”为A，相应死亡概率 为π。记事件“白鼠用药后不死亡”为 ，相 应不死亡概率为1-π。设实验后3只白鼠中死亡 的白鼠数为X，则X的可能取值为0，1，2和3，
例 实验白鼠3只，白鼠用药后死亡的死亡概率 π=0.6，则3只白鼠中死亡鼠数X的总体均数为

7.4.1二项分布课件共28张PPT

7.4.1二项分布课件共28张PPT
示事件A发生的次数，则X的分布列为
= = × × ( − )− ， = , , …,n.
如果随机变量X的分布列具有上式的形式，则称随机变量X服从二项分布（binomial
distribution），记作X~B(n,p).
X
p
0
0
n
1
0
n
1 n 1
C pq C pq
解法2：采用3局2胜制，不妨设赛满3局，用X表示3局比赛中甲胜的局数，则X～B(3，0.6).
甲最终获胜的概率为 =P(X=2)+P(X=3)= × . × . + × . =0.648.
采用5局3胜制，不妨设赛满5局，用X表示5局比赛中甲胜的局数，则X～B(5，0.6).甲最终获胜的概
小木钉后下落的方向,有“向左下落”和“向右
下落”两种可能结果,且概率都是0.5.在下落的
过程中,小球共碰撞小木钉10次,且每次碰撞后下
落方向不受上一次下落方向的影响,因此这是一
个10重伯努利试验,小球最后落入格子的号码等
于向右落下的次数,因此X服从二项分布。
典型例题
例2：如图是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但
1
n
…ቤተ መጻሕፍቲ ባይዱ
k
…
C nk p k q n k
…
…
n
C nn p n q 0
1.二项分布中，各个参数的意义？
n：重复试验的次数；k：事件A发生的次数；p：在一次试验中，事件A发生的概率.
2.判断一个随机变量是否服从二项分布，关键有两点：
一是对立性，即一次试验中，事件发生与否两者必有其一；
二是重复性，即试验是独立重复地进行了n次.

二项分布公开课课件

二项分布公开课课件
概率生成函数是二项式定理的推广，用于计算在n次独立重复 试验中，随机事件恰好发生k次的概率，其公式为P(X=k) = [T^(k)] * (p * (1-p))^n，其中T是试验次数，p是随机事件发 生的概率。
均值和方差
01
均值和方差是二项分布的两个重 要数学特征，用于描述随机事件 的平均值和波动性。
02
二项分布的均值是n*p，表示在n 次独立重复试验中随机事件平均 发生的次数；方差是n*p*q，表 示随机事件的波动程度，其中q表 示随机事件不发生的概率。
二项分布的参数
二项分布的参数包括试验次数n和随机事件发生的概率p， 它们共同决定了随机事件的分布形态。
试验次数n表示独立重复试验的总次数，随机事件发生的 概率p表示每次试验中随机事件发生的可能性大小。当n和 p一定时，二项分布的形态就确定了。
二项分布在现实生活中的应用
成功率预测
在生产、科研等活动中，可以通过二 项分布来预测多次试验中成功的次数 。
风险评估
生物统计学
在生物统计学中，二项分布被广泛应 用于遗传学、流行病学等领域，例如 研究疾病的发病率、遗传规律等。
在金融、保险等领域，可以通过二项 分布来评估风险和预测未来的结果。
02
二项分布的数学模型
THANKS。
利用Excel或数学软件计算
利用Excel或数学软件计算是一种便捷的二 项分布计算方法，通过利用现成的软件工具 进行计算。
Excel和许多数学软件都提供了二项分布的 计算功能，用户只需要输入相应的参数（如 试验次数、成功的概率等），软件就会自动 计算出二项分布的概率。这种方法省去了手 动计算的繁琐过程，提高了计算的准确性和 效率。同时，对于一些复杂的二项分布问题 ，利用软件进行计算可以避免复杂的数学推

高二数学二项分布PPT精品课件

高二数学二项分布PPT精品课件

判断下列试验是不是独立重复试验：
1).依次投掷四枚质地不同的硬币,3次正面向上; 2).某人射击,击中目标的概率是稳定的,他连续射击
了10次,其中6次击中; 3).口袋装有5个白球,3个红球,2个黑球,从中依次
抽取5个球,恰好抽出4个白球; 4).口袋装有5个白球,3个红球,2个黑球,从中有放回
的抽取5个球,恰好抽出4个白球
情境创设
俺投篮，也是 讲概率地！！
第一投，我要努力！
Ohhhh，进球拉！！！
第二投，动作要注意！！
又进了，不愧 是姚明啊 ！！
第三投，厉害了啊！！
第三次登场了！
这都进了！！ 太离谱了！
第四投，大灌蓝哦！！
……
姚明作为中锋，他职业生涯的罚球 命中率为0．8，假设他每次命中率相同, 请问他4投3中的概率是多少?
请举出生活中碰到的独 立重复试验的例子。
学生活动
问题1：在4次投篮中姚明恰好命中1次的概率是多少? 分解问题：1)在4次投篮中他恰好命中1次的情况有几种?
2)说出每种情况的概率是多少? 3)上述四种情况能否同时发生?
表示投中, 表示没投中,则4次投篮中投中 1次的情况有以下四种:
(1) (2) (3) (4)
0
1
2
3
0.0016 0.0256 0.1536 0.4096
4
0.4096
(2)两人进球数相等的概率是多少?
变式9.姚明投篮一次,命中率为0.8,有学生认为他投 10次篮就肯定会投中8个. 请你分析一下,这位同学 的想法正确吗?
小结提高 概率
独立重复试验
投球 概念
核心
分类讨论•特殊到一般
二项分布
应用ቤተ መጻሕፍቲ ባይዱ

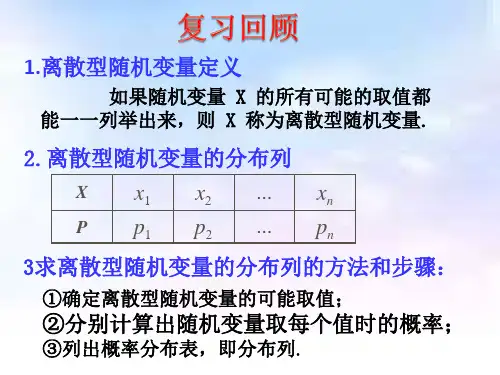
二项分布(上课)ppt课件

二项分布(上课)ppt课件
【分析】
（1）有放回的抽取，则每次抽到白球的概率相同， 黑球个数x服从二项分布；
（2）无放回的抽取，则每次抽到白球的概率不同，
黑球个数x服从超几何分布；
（1）P1
C32
3 8
2
5 8
135 512
(2)P2
C32C51 C83
15 56
二项分布与超几何分布有什么区别和联系？
一个袋中放有 M 个红球，( N M )个白球，依次从袋中取n 个球，记下红球的个数 .
1.离散型随机变量定义
如果随机变量 X 的所有可能的取值都 能一一列举出来，则 X 称为离散型随机变量.
2.离散型随机变量的分布列
X
x1
x2
…
xn
P
p1
p2
…
pn
3求离散型随机变量的分布列的方法和步骤：
①确定离散型随机变量的可能取值；
②分别计算出随机变量取每个值时的概率；
③列出概率分布表，即分布列.
变式二:5次中恰有3次针尖向上的概率是多少？
引申推广:
P C53 0.63 (1 0.6)53
连续掷n次，恰有k次针尖向上的概率是
P Cnk 0.6k (1 0.6)nk
定义建构
一般地，在 n 次独立重复试验中，
用X表示事件A发生的次数，设每次试验中
事件Ａ发生的概率为p，则:
P
(X
k)
P
(X
k)
C
k n
pk
(1
p)nk
（其中k = 0，1，2，···，n ）
此时称随机变量X服从二项分布，记X~B(n,p) 并称p为成功概率。
基础训练 成功体验
一名学生骑自行车上学，从他家到学校的途中有3个交通

高二下学期数学人教A版选择性必修第三册7.4.1二项分布课件(3)

高二下学期数学人教A版选择性必修第三册7.4.1二项分布课件(3)
新课引入
大家还记得相互独立事件吗？怎样算相互独立事件？
P(AB)=P(A)P(B)
大家还记得二项式定理吗？通项是怎样的？
Tk 1 C a
k
n
nk
b
k
课堂探究
3
我们把只包含两个可能结果的实验叫做伯努利实验.
我们将一个伯努利实验独立地重复进行n次所组成的随机实验称
为n重伯努利实验.
n重伯努利实验具有如下共同特征:
布。记作X~B(n,p).
课堂探究
n
二项散布的概率和
n
P( X k ) C
k 0
等于1吗？怎么证明？
k 0
k
n
p (1 p)
k
nk
课堂探究
由二项式定理,易得
n
n
P( X k ) C
k 0
k 0
k
n
p (1 p)
k
[ p (1 p)]
1
问题的概率都为0.6,皮匠中至少一人解出题目即胜出比赛,问臭
皮匠团队和诸葛亮哪个胜出的可能性大?
解:设皮匠中解出题目的人数为X,则X~B(3,0.6)
皮匠中至少一人解出题目的概率
P( X 1) P( X 1) P( X 2) P( X 3)
C 0.6 (1 0.6)
部的格子中.格子从左到
右分别编号为0，1，2，…，10，
用X表示小球最后落入格子的号
码，求X的散布列。
0 1 2 3 4 5 6 7 8 9 10
例题解析
分析：小球落入哪个格子取决于在下落过程中与各小木钉
碰撞的结果,设实验为视察小球碰到小木钉后下落的方向,有“向左下落”

人教版高二下数学选择性必修第三册-7.4 二项分布与超几何分布(第4课时)【课件】

人教版高二下数学选择性必修第三册-7.4 二项分布与超几何分布(第4课时)【课件】

年龄
20以下 [20，30) [30，40) [40，50) [50，60) [60，70]
使用人数
3
12
17
6
4
2
未使用人数
0
0
3
14
36
3
(1)现随机抽取1名顾客，试估计该顾客年龄在[30，50)且未使用自由购的概
率；
(2)从被抽取的年龄在[50，70]且使用自由购的顾客中，随机抽取 3 人进一步 了解情况，用 X 表示这 3 人中年龄在[50，60)的人数，求随机变量 X 的分布列及 数学期望；
∴X的分布列为：
X
0
1
2
P
63 130
28 65
11 130
(3)根据样本估计总体的思想，任取1件产品，该产品的质量超过505克的概
率为1420＝130.
从流水线上任取2件产品互不影响，该问题可看成2重伯努利试验，Y的可能
取值为0，1，2，且Y～B2，130，P(Y＝k)＝C2k130k1－1302－k，所以P(Y＝0)＝
(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率； (2)用X表示接受乙种心理暗示的女志愿者人数，求X的分布列与数学期望 E(X)． 【解析】 (1)记接受甲种心理暗示的志愿者中包含A1但不包含B1的事件为 M，则P(M)＝CC18045＝158. (2)由题意知X可取的值为0，1，2，3，4，则 P(X＝0)＝CC16055＝412，P(X＝1)＝CC641C0541＝251， P(X＝2)＝CC631C0542＝1201，P(X＝3)＝CC621C0543＝251，
所以X的分布列为：
X1 2 3
P
1 5
3 5

二项分布-高中数学课件

二项分布-高中数学课件

解：设A＝“正面朝上”，则P(A)＝0.5. 用X表示事件A发生的次数，
则 X ~ B(10, 0.5).
(1) 恰好出现5次正面朝上的概率为
P(X
5)
C150
0.55
(1 0.5)5
252 1024
63 256
(2) 正面朝上出现的频率在[0.4, 0.6]内等价于4≤X≤6，于是所求概率为
4
3 4
1
3 4
3
C41
3 4
1
1
3 4
41
.
PX
k
P Bk
C4k
3 k 4
1
3 4k 4
k
0,1,2,3,4 .
X的分布列就可以写成如表的形式：
X
0
1
2
3
4
P
C40
3 4
0
1
3 4 4
C41
3 4
1
1
2
1
3 4
2C43
3 4
3
1
3 4
当n=1时，可以得到两 点分布的分布列如右 表：
X
0
1
P 1 p p
两点分布是一种特殊的二项分布，即是n=1的二项分布； 二项分布可以看做两点分布的一般形式.
典例解析
例1 将一枚质地均匀的硬币重复抛掷10次，求:
(1) 恰好出现5次正面朝上的概率；
(2) 正面朝上出现的频率在[0.4, 0.6]内的概率.
Cnk pk qnk
C
n n
p
nq
0
此时称随机变量X服从二项分布，记作 X~B(n,p),并称p为成功概率。
追问 二项分布和两点分布有什么联系？

人教版高二下数学选择性必修第三册-7.4 二项分布与超几何分布(第1课时)【课件】

人教版高二下数学选择性必修第三册-7.4 二项分布与超几何分布(第1课时)【课件】
故所求概率为P＝C31×353×1－352＝3312245.
思考题2 某气象站天气预报的准确率为80%，计算(结果保留到小数点后
第2位)： (1)5次预报中恰有2次准确的概率； (2)5次预报中至少有2次准确的概率； (3)5次预报中恰有2次准确，且其中第3次预报准确的概率．
【思路分析】
【解析】 令X表示5次预报中预报准确的次数，则X～B 5，45 ，故其分布
∴P(X＝1)＝C51×12×1－124＝352.
(2)令1－p＝q，根据二项式定理，P(X＝0)＋P(X＝1)＋P(X＝2)＋…＋P(X＝ n)＝Cn0p0qn＋Cn1p1qn－1＋Cn2p2qn－2＋…＋Cnnpnq0＝(q＋p)n.
因为p＋q＝1，所以P(X＝0)＋P(X＝1)＋P(X＝2)＋…＋P(X＝n)＝1， 即分布列P(X＝k)＝Cnkpk(1－p)n－k，k＝0，1，2，…，n满足性质 k∑＝n 0 Cnkpk(1－ p)n－k＝[(1－p)＋p]n＝1.
【解析】 (1)由于试验的条件不同(质地不同)，因此不是n重伯努利试验． (2)某人射击击中目标的概率是稳定的，因此是n重伯努利试验． (3)每次抽取，试验的结果有三种，因此不是n重伯努利试验． 探究1 n重伯努利试验的判断依据 (1)要看该试验是不是在相同的条件下可以重复进行． (2)每次试验相互独立，互不影响． (3)每次试验都只有两种结果，即事件发生或不发生．
(3)“5次预报中恰有2次准确，且其中第3次预报准确”的概率为C41×
4 5
×
1－453×45≈0.02.
题型三 二项分布及其均值与方差
例3
(1)若离散型随机变量X～B(n，p)，且E(X)＝
5 2
，D(X)＝
5 4

人教版高中数学选择性必修3《二项分布》PPT课件

人教版高中数学选择性必修3《二项分布》PPT课件
2 3 19
相当于 3 次独立重复试验,故 P(A)=1-P()=1-( ) = .
3 27
(2)记“甲恰有 2 次击中目标”为事件 B,“乙恰有 1 次击中目标”为事件 C,则
22 4
3
3 3
1
P(B)=( ) = ,P(C)=C2 × ×(1- )= ,由于甲、乙射击相互独立,
3 9
4
4 8
4 3 1
2
× =
1
,故
4
ξ~B
1
10, 4
.因此
微思考
在n次独立重复试验中,各次试验的结果相互有影响吗?
提示 在n次独立重复试验中,各次试验的结果相互之间无影响.因为每次试
验是在相同条件下独立进行的,所以第i+1次试验的结果不受前i次结果的
影响(其中i=1,2,…,n-1).
课堂篇 探究学习
探究一
n重伯努利试验概率的求法
延伸探究2在本例(2)的条件下,求甲未击中,乙击中2次的概率.
解 记“甲未击中目标”为事件 M,“乙击中 2 次”为事件 N,
22 1
32 9
则 P(M)=(1- ) = ,P(N)=( ) = ,所以甲未击中、乙击中 2 次的概率为
3 9
4 16
1
9
1
P(MN)=9 × 16 = 16.
反思感悟n重伯努利试验概率求法的三个步骤
变式训练2某人投篮命中率为0.8,重复5次投篮,命中次数为X,命中一次得3
分,求5次投篮得分的均值.
解 设投篮得分为变量η,则η=3X.
依题意,X~B(5,0.8),则E(X)=5×0.8=4,故E(η)=3E(X)=12.
探究三
二项分布的应用

7.4.1二项分布课件-高二下学期数学人教A版选择性必修第三册

7.4.1二项分布课件-高二下学期数学人教A版选择性必修第三册
D(X ) 02 (1 p)2 12 2 p(1 p) 22 p2 (2 p)2 2 p(1 p) .
一般地，可以证明： 如果 X ~B(n ，p) ，那么 E(X ) np ，D(X ) np(1 p) .
下面对均值进行证明.
令 q 1 p ，由 kCkn nCkn11 ，
先考察 n 较小的情况. （1）当 n 1时，X 服从两点分布，分布列为 P(X 0) 1 p ， P(X 1) p .均值和方差分别为 E(X ) p ，D(X ) p(1 p) . （2）当 n 2 时，X 的分布列为 P(X 0) (1 p)2 ，P(X 1) 2 p(1 p) ， P(X 2) p2 .均值和方差分别为 E(X ) 0 (1 p)2 1 2 p(1 p) 2 p2 2 p .
21 32
.
例 2 甲、乙两选手进行象棋比赛，如果每局比赛甲获胜的概率为 0.6， 乙获胜的概率为 0.4，那么采用 3 局 2 胜制还是采用 5 局 3 胜制对甲更有利？
解法 1：采用 3 局 2 胜制，甲最终获胜有两种可能的比分 2 : 0 或 2:1 ，前 者是前两局甲连胜，后者是前两局甲、乙各胜一局且第 3 局甲胜.因为每局比 赛的结果是独立的，甲最终获胜的概率为 p1 0.62 C12 0.62 0.4 0.648 .
面摸出的一定是红球，最后一次是白球，不符合二项分布的定义； ④n 次试验是不独立的，因此 不服从二项分布.故选 B.
2. 某人通过普通话二级测试的概率是 1 ，若他连续测试 3 次(各次测试互不影响)， 4
则其中恰有 1 次通过的概率是( C )
A. 1
B. 1
C. 27
D. 3
64
16
64
4
解析：某人通过普通话二级测试的概率是 1 ，他连续测试 3 次，其中恰有 1 次通过 4

7.4.1 二项分布 课件-高二下学期数学人教A版(2019)选择性必修第三册

7.4.1 二项分布 课件-高二下学期数学人教A版(2019)选择性必修第三册
7.4.1 二项分布
知识准备
1.两点分布列
X
0
1
P
1－P
P
2.二项展开式的通项第 + 1 项为
Tk 1 Cnk a nk b k
二项式定理和二项分布有什么联系？
n重伯努利试验的概念
在实际问题中，有许多试验与掷硬币试验具有相同的特征，它们只
包含两个可能的结果.例如
掷一枚硬币结果为正面向上或反面向上；
问题：假设随机变量X~B(n，p)，那么X的均值和方差各是什么？
证明：若X~B(n，p)，则E(X)=np
令q 1 p,由kCnk nCnk11 , 可得
n
E ( X ) kC p q
k
n
k 0
k
nk
n
nC
k 0
k 1
n 1
n
p q np Cnk11 p k 1q n1( k 1)
(3)一批产品的次品率为5%,有放回地随机抽取20次.观察取出的次品数
解:
随机
试验
是否是n重伯
努利试验
伯努利试验
(1)
是
抛掷一枚质地均匀的硬币
(2)
是
(3)
是
P(A)
重复试验
的次数
10
某飞碟运动员进行射击
1
2
0.8
3
从一批产品中随机抽取一件
0.05
20
深化概念理解
在n重伯努利试验中,"在相同条件下"等价于各次试验的结果不会受其他
如果随机变量的分布列具有上式的形式，则称随机变量服从二项分布，
记作~(，).
BC
伯努利分布（二项分布）的概念

7.4.1二项分布课件——高二下学期数学人教A版选择性必修第三册

7.4.1二项分布课件——高二下学期数学人教A版选择性必修第三册
√
n重伯努利实验概率求解的三个步骤(1)判断：根据n重伯努利实验的特征，判断所给实验是否为伯努利实验．(2)分拆：判断所求事件是否需要分拆．(3)计算：就每个事件根据n重伯努利实验的概率公式求解，最后利用互斥事件的概率加法差各是什么？
1.抛一枚硬币的结果2.检验一个产品是否为合格品3.射击中靶或者脱靶以上问题有哪些共同特征？
我们把只包含两个可能结果的实验叫做伯努利实验。
1.伯努利实验
点拨精讲（24分钟）
2.n重伯努利实验
我们将一个伯努利实验独立地重复进行n次所组成的随机实验成为n重伯努利实验。
n重伯努利实验具有如下共同的特征：（1）同一个伯努利实验重复做n次；（2）各次实验结果相互独立。
各次实验成功的概率相同
探究：某飞碟运动员每次射击中靶的概率为0.8，连续3次射击，中靶次数X的概率散布列是怎样的？
11:11:34
3.二项散布
例1 将一枚质地均匀的硬币重复抛掷10次，求: (1) 恰好出现5次正面朝上的概率； (2) 正面朝上出现的频率在[0.4, 0.6]内的概率.
解：
设A＝“正面朝上”，则P(A)＝0.5. 用X表示事件A产生的次数， 则 X ~ B(10, 0.5).(1) 恰好出现5次正面朝上的概率为
(2) 正面朝上出现的频率在[0.4, 0.60内等价于4≤X≤6，于是所求概率为
随机变量X服从二项散布的三个前提条件：
(1) 每次实验都是在同一条件下进行的；(2) 每一次实验都彼此相互独立；(3) 每次实验出现的结果只有两个，即某事件要么产生，要么不产生.
7.4二项散布与超几何散布 7.4.1二项散布
学习目标（1分钟）
1.了解伯努利实验
2.掌握二项散布及其数字特征，并能解决简单的实际问题
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

练习 4:一袋中装有 5 个白球，3 个红球，现从袋中往外取球， 每次取一个，取出后记下球的颜色，然后放回，直到红球出 现 10 次时停止，停止时取球的次数 是一个随机变量，试 求 的概率.
P(
)
C191 39 52 3 812
C191
(
3 8
)10
(
5 8
)2
课外思考:
巴拿赫(Banach)火柴盒问题
4.某射手有5发子弹，射击一次命中的概率为0.9,如 果思命考中2了解就: 停止射击，否则一直射击到子弹用完，
求耗用子弹数 的分布列.
解： 的所有取值为：1、2、3、4、5
P( 1) 0.9
P( 2) 0.1 0.9
P( 3) 0.12 0.9 P( 4) 0.13 0.9
知他解 1 道题的正确率为 0.6，试求他能及格的概率(保留 2
位小数)。
C54 0.64 0.4 C55 0.65 0.34
3.某人对一目标进行射击，每次命中率都是 0.25，若使至少 命 中 1 次 的 概 率 不 小 于 0.75 ， 至 少 应 射 击 几 次 ？ （ lg 2 0.3010, lg 3 0.4771 ）
8 16 16 2 答：按比赛规则甲获胜的概率为 1 ．
2
学.科.网
▪ 例2、100件产品中有3件不合格品，每次取 一件，又放回的抽取3次，求取得不合格品 件数X的分布列。
练习2、某厂生产电子元件，其产品的次品率 为5%．现从一批产品中任意地连续取出2件，
写出其中次品数ξ的概率分布．
练习巩固：
解：甲、乙两队实力相等，所以每局比赛甲获胜的概率为
1 ，乙获胜的概率为 1 ．
2
2
⑴甲打完 5 局才能取胜,相当于进行 5 次独立重复试验，
且甲第 5 局比赛取胜，前 4 局恰好 2 胜 2 负 新疆 王新敞 奎屯
∴甲打完 5 局才能取胜的概率
P1
C42
( 1 )2 2
( 1 )2 2
1 2
3 16
• 波兰数学家随身带着两盒火柴，分别放在
左、右两个衣袋里，每盒有n根火柴，每次
使用时，便随机地从其中一盒中取出一根。
试求他发现一盒已空时，另一盒中剩下的
火柴根数k的分布列。
P
Cn 2nk
1 2
2nk
,
k
Hale Waihona Puke 0,1,2,,n
2. n 重贝努利(Bernoulli)试验
若n 次重复试验具有下列特点：
1) 每次试验的可能结果只有两个A 或 A,
打开这个门,他随机地选取一把钥匙开门,即每次以
1 的 概 率 被 选 中, 求 该 人 在 第k次 打 开 门 的 概 率. n 解 令Bk表示第k次打开门,则
P ( Bk
)
(1
1 n
)k 1
1 n
k 1,2,
注:事件首次发生所需要的试验次数ξ服从几何分布
几
何ξ 1
2
3…
k…
分 布
P
p
pq
pq2 … pqk-1 …
此 时 称 随 机 变 量 X 服 从 二 项 分 布 （ binomial distribution）,记作 X~B(n, p)，并称 p 为成功概率.
注: Pn(k) cnk pkqnk是( p q)n 展开式中的第 k 1 项.
学.科.网
二项分布与两点分布、超几何分布有什么区别和联系？
1．两点分布是特殊的二项分布 (1 p)
3答案
3．某人对一目标进行射击，每次命中率都是
0.25，若使至少命中 1 次的概率不小于 0.75，至
少应射击几次？（ lg 2 0.3010, lg 3 0.4771 ）
解：设要使至少
命中
1
次的概率不小于
0.7
5，应射击
n
次 新疆
王新敞
奎屯
记事件 A ＝“射击一次，击中目标”，则 P(A) 0.25 ．
例1:1名学生每天骑自行车上学,从家到学校的途中有5个 交通岗,假设他在交通岗遇到红灯的事件是独立的,并且概 率都是1/3.(1)求这名学生在途中遇到3次红灯的.(2)求这 名学生在途中至少遇到一次红灯的概率.
解:记ξ为学生在途中遇到红灯次数，则 ~ B(5, 1)
(1)遇到3次红灯的概率为：
3
P(
1．每次试验的成功率为 p(0 p 1) ，重复进行 10 次试验，
C 其中前 7 次都未成功后 3 次都成功的概率为（ ）
(A) C130 p3 (1 p)7 (B) C130 p3 (1 p)3 (C) p3 (1 p)7 (D) p7 (1 p)3
2．某人参加一次考试，若 5 道题答对 4 道题则为及格，已
独立重复试验 与二项分布
学.科.网
n 次独立重复试验: 一般地,在相同条件下，重复做的 n 次试验称
为 n 次独立重复试验.
在 n 次独立重复试验中，记 Ai 是“第 i 次试 验的结果”
P( A1 A2 An ) = P( A1 )P( A2 ) P( An )
“相同条件下”等价于各次试验的结果不会受其他试 验的影响。
3)
C53
(
1 3
)3
(
2 3
)2
40 243
(2)至少遇到一次红灯的概率为:
P 1 1 P 0 1 ( 2)5 211 .
3 243
学.科.网
练习 1 实力相等的甲、乙两队参加乒乓球团体比赛，规 定 5 局 3 胜制（即 5 局内谁先赢 3 局就算胜出并停止比赛）． ⑴试求甲打完 5 局才能取胜的概率． ⑵按比赛规则甲获胜的概率．
“ 5”表示前四次都没射中 P( 5) 0.14
故所求分布列为:
1
2 345
P
0.9 0.10.9 0.12 0.90.13 0.9 0.14
小结提高 概率
独立重复试验
投球 概念
核心
分类讨论•特殊到一般
二项分布
应用
作业
➢课后练习A\B两组
思考
一个人开门, 他共有n把钥匙,其中仅有一把能
.
(2) 记事件 A “甲打完 3 局才能取胜”， 事件 B =“甲打完 4 局才能取胜”， 事件 C =“甲打完 5 局才能取胜”． 事 件 D ＝ “ 按 比 赛 规 则 甲 获 胜 ”， 则
D A B C ，又因为事件 A 、 B 、 C 彼此互斥， 故 P(D) P( A B C) P( A) P(B) P(C) 1 3 3 1．
2．一个袋中放有 M 个红球，( N M )个白球，依次从袋中 取 n 个球，记下红球的个数 .
⑴如果是不放回地取, 则 服从超几何分布.
P(
k)
C C k nk M NM
C
n N
(k
0,1, 2,
, m) (其中 m min(M , n)
⑵如果是有放回地取，则 B(n, M )
N
学.科.网
∵射击 n 次相当于 n 次独立重复试验，
∴事件 A 至少发生 1 次的概率为 P 1 Pn (0) 1 0.75n ．
由题意，令1 0.75n ≥0.75，∴ (3)n ≤ 1 ， 44
lg 1
∴
n≥
lg
4 3
4.82
，∴
n
至少取
5．
4
答：要使至少命中 1 次的概率不小于 0.75，至少应射击 5 次 新疆 王新敞 奎屯
问题 1 的推广: 一般地, 在 n 次独立重复试验中,用 X 表示事件
A 发生的次数，设每次试验中事件 A 发生的概率是 p ， 那么事件 A 恰好发生 k 次的概率 Pn (X=k) 是多少呢?
Pn (X=k )
C
k n
pk (1
p)nk
或
Pn (X=k )
C
k n
pkqnk
（其
中 q 1 p ,一次试验中事件 A 发生的概率为 p）．
且 P( A) p, P( A) 1 p ( 在各次试验中p是常数，保持不变） 2) 各次试验的结果相互独立， 则称这n次重复试验为n重贝努里试验，简称为 贝努里概型.