机械振动基础知识培训PPT(86张)

高三第一轮复习《机械振动和机械波》一、机械振动： （一）夯实基础：1、简谐运动、振幅、周期和频率：（1）简谐运动：物体在跟偏离平衡位置的位移大小成正比，并且总指向平衡位置的回复力的作用下的振动。

特征是：F=-kx,a=-kx/m （2）简谐运动的规律：①在平衡位置：速度最大、动能最大、动量最大；位移最小、回复力最小、加速度最小。

②在离开平衡位置最远时：速度最小、动能最小、动量最小；位移最大、回复力最大、加速度最大。

③振动中的位移x 都是以平衡位置为起点的，方向从平衡位置指向末位置，大小为这两位置间的直线距离。

加速度与回复力、位移的变化一致,在两个“端点”最大，在平衡位置为零，方向总是指向平衡位置。

④当质点向远离平衡位置的方向运动时，质点的速度减小、动量减小、动能减小，但位移增大、回复力增大、加速度增大、势能增大，质点做加速度增大减速运动；当质点向平衡位置靠近时，质点的速度增大、动量增大、动能增大，但位移减小、回复力减小、加速度减小、势能减小，质点做加速度减小的加速运动。

④弹簧振子周期：T= 2 (与振子质量有关,与振幅无关)（3）振幅A ：振动物体离开平衡位置的最大距离称为振幅。

它是描述振动强弱的物理量, 是标量。

（4）周期T 和频率f ：振动物体完成一次全振动所需的时间称为周期T,它是标量，单位是秒；单位时间内完成的全振动的次数称为频率，单位是赫兹（Hz ）。

周期和频率都是描述振动快慢的物理量，它们的关系是：T=1/f. 2、单摆：（1）单摆的概念：在细线的一端拴一个小球，另一端固定在悬点上，线的伸缩和质量可忽略，线长远大于球的直径，这样的装置叫单摆。

（2）单摆的特点：○1单摆是实际摆的理想化，是一个理想模型; ○2单摆的等时性，在振幅很小的情况下，单摆的振动周期与振幅、摆球的质量等无关; ○3单摆的回复力由重力沿圆弧方向的分力提供，当最大摆角α<100时，单摆的振动是简谐运动，其振动周期T=gL π2。

二、振幅、周期和频率从容说课本节课讲述描述简谐运动的振幅、周期和频率等几个物理量.它是上节课对简谐运动研究的延续,在上节课的基础上引进振幅用来直接反映简谐运动中的最大位移,间接反映简谐运动的能量,引进周期和频率用来反映简谐振动重复运动的快慢.只有切实理解了本节所学的几个物理量,才能更好地、更全面地反映出简谐运动的运动特征.尤其对以后的学习会起到很重要的作用.例如：对交变电流、电磁振荡等知识的学习.结合本节内容的特点,对本节教学的目标定位于：1.知道周期、振幅、频率三个物理量的定义,并理解其物理意义.2.理解周期与频率的关系，并能对二者进行换算．3.知道物体振动固有周期和固有频率．本节课的教学重点在于对周期、频率、振幅的认识和理解．本节课的教学难点是理解振幅与简谐运动能量的定性关系.以及振幅与位移的区别.为了突出重点、突破难点。

使学生能更好地接受知识，本节课采用先学后教、实验演示、讨论总结等方法。

以加深学生的理解,同时采用多媒体辅助教学,以激发学生的学习兴趣，达到圆满完成教学任务的目的．本节课的教学顺序确定如下：复习提问→新课导人→指导自学→归纳总结→强化练习→小结．一、知识目标 _1.知道描述简谐运动的周期、振幅、频率三个物理量．2.理解周期与频率的关系,并能进行两者间的换算．3.了解物体振动的固有周期和固有频率．二、能力目标1.培养学生对知识的归纳、总结能力.2.提高学生对实验的观察、分析能力.三、德育目标通过对简谐运动周期性的学习,使学生理解社会新旧更替.螺旋前进的道理。

教学重点对简谐运动周期、频率、振幅的认识和理解．教学难点1.理解振幅间接反映振动能量的理论依据．2.区分振幅与位移两个物理量．教学方法指导性自学、实验演示、多媒体辅助相结合的综合教学法．教学用具投影片、弹簧振子、秒表、CAI课件课时安排l课时教学过程一、新课导入1.复习提问①什么叫机械振动?②什么叫简谐运动?2.导人通过上节的学习,我们知道了什么是简谐运动,但如何对简谐运动来进行定性的描述和定量的计算呢?这就需要我们引进一些能反映简谐运动特性的物理量——周期、频率和振幅，本节我们就共同来学习这些物理量．二、新课教学(一)振幅、周期和频率．基础知识请学生阅读课文第一部分，同时思考下列问题：[投影片出示]1.什么叫振幅?其物理意义是什么?单位又是什么?用什么符号表示?2.什么叫周期?其物理意义是什么?单位又是什么?用什么符号表示?3.什么叫频率?其物理意义是什么?单位又是什么?用什么符号表示?学生阅读后,得出以上问题的结论：1.a.振动物体离开平衡位置的最大位移叫振幅．b.振幅用来反映振动物体振动的强弱．c.振幅的单位是：米(m)．d.振幅的符号是：A．2.a.做简谐运动的物体完成一次全振动所需要的时间叫周期．b.周期是用来反映物体振动快慢的物理量．c.周期的单位是：秒(s)．d.周期常用符号：T．3.a.做简谐运动的物体，在单位时间内完成全振动的次数叫频率．b.频率是用来反映物体振动快慢的物理量．c.频率的单位是：赫兹(Hz)．d.频率的常用符号：f．深入探究请同学们结合前面所学，考虑以下问题：[投影出示]1.振幅与位移有何区别，有何联系?2.周期与频率有何区别，有何联系?3.试以弹簧振子为例描述一次全振动．学生经过思考、讨论、归纳总结后得出上述问题的结论：1.振幅与位移的区别：a.物理意义不同．振幅是用来反映振动强弱的物理量；位移是用来反映位置变化的物理量．b.矢量性不同.振幅是一标量,只有大小,没有方向；位移是一矢量,既有大小又有方向．振幅与位移的相同点：a.都是反映长度的物理量.振幅是偏离平衡位置的最大距离；位移是偏离平衡位置的距离．其单位都是长度单位．b.位移的最大值就是振幅．2.周期与频率的区别：a.物理意义不同.周期是完成一次全振动所需要的时间；频率是单位时间内完成的全振动的次数．b.单位不同.周期的国际单位是秒；频率的国际单位是赫兹．周期与频率的联系：a.都是用来反映振动快慢的物理量.周期越大,振动得越慢；频率越大,振动得越快.b.周期与频率互成倒数关系．即：T=1．f①O→A→O→A′→O②A→O→ A′→O→A③A′→O→A→O→A′④O→A′→O→A→O教师总结通过上面的学习，我们对描述简谐运动的三个物理量：振幅、周期、频率，已有了一定的认识.下面我们简单应用一下．基础知识应用1.弹簧振子在B、C间做简谐运动，O为平衡位置，BC间距离为10 cm，B→C运动时间为1 s，如图所示.则 ( )A．从O→C→O振子做了一次全振动B.振动周期为1s,振幅是10cmC.经过两次全振动．通过的路程是 20cmD.从B开始经3s，振子通过路程是30cm2.一个弹簧振子.第一次把弹簧压缩x后开始振动.第二次把弹簧压缩2x后开始振动,则两次振动的周期之比和最大加速度的大小之比为（）A.1：2，1：2B.1:1,1:1C.1:2,1:2D.1:2,1:13.一个做简谐运动的质点,先后以同样大小的速度通过相距10 cm的A、B两点，历时0.5 s.如图所示,经过B点后再经过t=0.5 s 质点以方向相反、大小相同的速一次通过B点．则质点振动的周期是( )A.0.5 s，B.10sC.2.O sD.4.0s[参考答案]1.解析：振子从0→C→0时位移虽然相同,但速度的方向不同,振动只是半次全振动故A错.振子从B→c是半次全振动，故周期T=2 s，振幅A=OB=BC =52cm．故B错．由全振动的定义知：振子由B→C→B为一次全振动,振子路程s=4 A＝4× 5＝20 cm,所以两个全振动的路程中2×20cm=40cm,故C错。

1.机械振动：（1）：机械振动即物体（或物体的一部分）在某一中心位置两侧所做的往返的运动 （2）：回复力F 回：指向“平衡”位置的合力叫回复力 （3）：振动位移x ：都以“平衡”位置为位移的起点（4）：振幅A ：振动物体离开“平衡”位置的最大距离，振幅越大，振动的能量就越大 （5）：振动的周期T ：指完成一次全振动的时间；周期表示振动的快慢，周期小表示振动的快 （6）：振动的频率f ：指单位时间内完成振动的次数；频率大，表示振动的快。

单位为：赫兹（Hz ） （7）：T=f1；振动的周期T 的大小与振幅的大小无关：对于同一个振动系统，当振动的振幅变大时，其周期将保持不变，所以物体振动的周期又叫固有周期（8）:平衡位置：振动的中心位置，是假冒的“平衡”，F 合不一定为0，如：单摆的“平衡”位置的加速度为：022≠==⇒==mF R vR v a m F F 指向圆心的合力向心向心指向圆心的合力2：简谐振动：（1）：回复力F 回和位移x 成正比，但它们的方向相反；F 回＝-kxx 为物体离开“平衡”位置的位移 负号表示回复力F 回和位移x 的方向相反 回复力就是一个指向“平衡”位置的合力（2）：对于同一个振动系统，当振动的振幅变大时，其周期仍保持不变 （3）：简谐振动的x-t 图像：是一条正弦或余弦曲线（4）：振动的周期T 的大小与振幅的大小无关（所以把它叫国有周期）。

弹簧振子的T 与小球的质量、弹簧的劲度序数有关；单摆的T 与摆长、重力加速度g 有关3.单摆（1）：当单摆的摆角小于80时，单摆的振动可以看做简谐振动（2）：单摆振动时，也可以把它看做圆周运动R m R m m F F T R v 2222）（向心指向圆心的合力πω====(多多从不同的角度分析问题)（3）：单摆的回复力由重力在切线方向的分力提供。

当摆角小于80时，Lx≈θsin ，mg F L x-=回复力（如右图）（3）：当单摆的摆角小于80时，gL T π2=L 为物体摆动时的圆心（悬点）到物体重心的距离g 为当地的重力加速度g ＝2R GM；g ´=222)()(H R gR H R GM ++=（g ´为离天体表面H 高处的重力加速度；g为天体表面的重力加速度；R 为天体的半经；M 为中心天体的质量；H 为离天体表面的高）公式说明T 与振幅A 无关（4）：单摆振动时，由于拉力始终与速度垂直，所以拉力不做功，如无阻力，则物体的机械能守恒 （5）：单摆振动时，如有阻力，则在短时间内，仍可把它看做简谐振动4、任何一个介质质点在一个周期内经过的路程都是4A ，在半个周期内经过的路程都是2A ，但在四分之一个周期内经过的路程就不一定是A 了(多多用位移时间图像帮助分析问题) 5、受迫振动：（1）：物体在周期性外力的作用下的振动叫受迫振动（2）：物体做受迫振动时，它的频率等于驱动力的频率，而跟物体的固有频率无关，如图：假如L=g ，则单摆的固有周期gLT π2==2π秒，如果每隔八秒推一下小球，则单摆的周期就为8秒，而不是2π秒（3）：波在传播时，各质点都在做受迫振动(各质点都在模仿波源的振动)，所以波由一种介质传到另一介质时，波的频率不变（等于波源的振动频率）（4）：物体在做受迫振动时，驱动力的频率跟物体的固有频率相等的时侯，物体的振幅最大，这种现象叫共振。

机械振动机械波专题一．机械振动基础知识：（一）机械振动产生振动的必要条件是：a、物体离开平衡位置后要受到回复力作用。

b、阻力足够小。

（二）简谐振动1. 定义：F=－kx，其中“－”号表示力方向跟位移方向相反。

2. 简谐振动的条件：物体必须受到大小跟离开平衡位置的位移成正比，方向跟位移方向相反的回复力作用。

3. 简谐振动是一种机械运动，它的位移、回复力、速度、加速度以及动能和势能（重力势能和弹性势能）都随时间做周期性变化。

（三）描述振动的物理量，简谐振动是一种周期性运动，描述系统的整体的振动情况常引入下面几个物理量。

1. 振幅：2. 周期和频率简谐振动的周期和频率是由振动物体本身性质决定的，与振幅无关，所以又叫固有周期和固有频率。

（四）单摆：摆角小于5°的单摆是典型的简谐振动。

（五）振动图象。

简谐振动的图象是振子振动的位移随时间变化的函数图象。

所建坐标系中横轴表示时间，纵轴表示位移。

图象是正弦或余弦函数图象，它直观地反映出简谐振动的位移随时间作周期性变化的规律。

要把质点的振动过程和振动图象联系起来，从图象可以得到振子在不同时刻或不同位置时位移、速度、加速度，回复力等的变化情况。

（六）阻尼振动、受迫振动、共振。

基础练习1.关于简谐振动的加速度，下列说法正确的是（）A.大小与位移成正比，方向一周期变化一次B.大小不变，方向始终指向平衡位置C.大小与位移成正比，方向始终指向平衡位置D.大小变化是均匀的，方向一周期变化一次2.一单摆摆长为l，若将摆长增加1m，则周期变为原来的1.5倍，可以肯定l长为（）A.2mB.1.5mC.0.8mD.0.5m3.对单摆的振动，以下说法中正确的是（）A.单摆摆动时，摆球受到的向心力大小处处相等B.单摆运动的回复力是摆球所受合力C.摆球经过平衡位置时所受回复力为零D.摆球经过平衡位置时所受合外力为零4.A、B两个弹簧振子，A的固有频率为f，B的固有频率为4f，若它们均在频率为3f的策动力作用下作受迫振动，则（）A.振子A的振幅较大，振动频率为fB.振子B的振幅较大，振动频率为3fC.振子A的振幅较大，振动频率为3fD. 振子B的振幅较大，振动频率为4f5．如图示，质量为m的砝码A放置在质量为M的滑块B上，B与弹簧相连，它们一Array起在光滑的水平面上作简谐运动，弹簧的劲度系数为k，砝码与滑块之间的动摩擦因数为，要使砝码与滑块在振动过程中不发生相对运动，问最大振幅等于多少？二．机械波基础知识波的理解1 介质和振源是形成机械波的两个充要条件,二者缺一不可.2 相同性质的机械波的速度由介质决定,波长由介质和振源共同决定.3 每一个参与振动的质点做的都是和振源同频率的受迫振动.4 当振源停止振动的时候,机械波不会马上停止传播.它会在介质中继续传播直到能量完全消耗掉为止.5. 波的干涉和衍射6 多普勒效应惠更斯原理7.波长、频率和波速的关系：v=fλ(波在任何介质中传播的频率是不变的)基础练习：1．区分横波和纵波是根据A．质点振动的振幅和波的传播速度的大小B．质点振动的频率和波的传播能量的多少C．质点振动的方向和波传播的远近D．质点振动的方向和波传播的方向2．如图所示，为波沿着一条固定的绳子向右刚传播到B点的波形，由图可判断出A点刚开始的振动方向是()A．向左B．向右C．向下D．向上3．如图10—1—2所示是沿绳向右传出的一列横波．在图上画出各个质点的振动速度方向，并回答下列几个问题：(1)速度最大的点是第_______点、第_______点；(2)第_______点所在的位置是波的波峰，此时该质点振动的速度为_______4．关于两列波的稳定干涉现象，下列说法正确的是（）A.任意两列波都能产生稳定干涉现象B.发生稳定干涉现象的两列波，它们的频率一定相同C.在振动加强的区域，各质点都处于波峰D. 在振动减弱的区域，各质点都处于波谷5.以下关于波的衍射的说法中正确的是（）A．波遇到障碍物时，一定会发生明显的衍射现象B．当障碍物的尺寸比波长大得多时，衍射现象很明显C．当孔的大小比波长小时，衍射现象很明显D．只有当障碍物的尺寸与波长相差不多时，才会发生明显的衍射现象6.关于多普勒效应,下列说法中正确的是（）A.多普勒效应是由波的干涉引起的B.多普勒效应说明波源的频率发生了改变C.多普勒效应是由于波源和观察者之间有相对运动而产生的D.只有声波才能产生多普勒效应振动图像和波动图像1.如图所示，（1）为某一波在t＝0时刻的波形图，（2）为参与该波动的P点的振动图象，则下列判断正确的是A.该列波的波速度为4m／s ；B．若P点的坐标为x p＝2m，则该列波沿x轴正方向传播C、该列波的频率可能为 2 Hz；D．若P点的坐标为x p＝4 m，则该列波沿x轴负方向传播；2.一列简谐横波在x轴上传播，图5所示的实线和虚线分别为和两个时刻的波的图象，已知波速为16m/s。

第一章绪论§1-1 引言机械振动是机械运动的一种特殊形式，是指物体在其平衡位置附近所作的往复运动。

年没课程的一些名着，如Thomson和Meirovitch的着作，在份量和叙述方式上都不尽合适。

针对少学时（约30～36学时）的工科本科生的需要，在1983～1996年期间对本科生和工程师短训班的十五次讲授中，博采国内外一些较好着作的内容，较好的叙述方式，曾三次编写“机械振动”讲义，试图使读者在学习中能做到：学习振动分析的基本理论和方法，掌握现代数学和电子计算机这一强有力工具的初步应用；随机振动入门，着重于基本概念及其数学方法的工程应用实例；噪声的基本概念和测试方法；…为今后进一步学习应用打下基础，但内容又不过多、过深，略去定量的证明和公式繁琐的推导。

“机械振动”讲义注重实用性、实例的重点阐述，计算机例题的上机操作求解等基本技能的训练。

第二章叙述常系数线性微分方程的基本解法。

在给工科专业高年级学生讲授振动课程第七章“随机振动入门”，介绍随机振动的数学应用，阶跃激励、脉冲激励和任意激励的响应—卷积积分（杜哈美积分）。

随机激励下响应的付利叶积分法。

随机振动理论的初步应用。

振动对人体的影响，ISO2631标准。

机车车辆工程和汽车工程的应用实例。

第八章“噪声的测量”，介绍声学及噪声的基础知识，噪声测量仪表，测量方法，并附有噪声测量实验指导书。

本讲义自1983年开始教学实践以来，经1987、1990、1997年三次修订而成。

由陈石华教授（第一至六章）、刘永明博士、副教授（第七章）、施绍祺高级工程师（第八章）编写，全书由刘永明制图、电脑排版。

由于时间仓促、水平有限，书中不妥之处，热诚地欢迎读者指正。

杂的控制系统。

由于振动，机器在使用过程中往往产生巨大的反复变动的载荷，这将导致机器使用寿命的降低，甚至酿成灾难性的破坏事故。

如大桥因共振而毁坏；烟囱因风振而倒坍；飞机因颤振而坠落等等，文献均有记载。

为了防止这些事故的发生，若不针对事故的原因作正确的分析和研究，设计人员往往传统方式地加大结构断面尺寸，导致机器重量增加和材料的浪费。

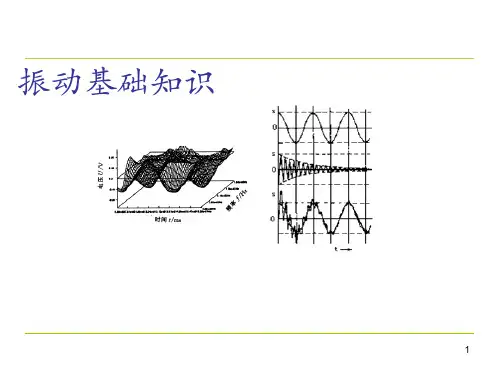
旋转机械振动分析基础汽轮机、发电机、燃气轮机、压缩机、风机、泵等都属于旋转机械，是电力、石化和冶金等行业的关键设备。

这些设备出现故障后，大多会带来严重的经济损失.振动在设备故障中占了很大比重，是影响设备安全、稳定运行的重要因素。

振动又是设备的“体温计”，直接反映了设备健康状况,是设备安全评估的重要指标.一台机组正常运行时，其振动值和振动变化值都应该比较小。

一旦机组振动值变大，或振动变得不稳定，都说明设备出现了一定程度的故障.振动对机组安全、稳定运行的危害主要表现在: （1)振动过大将会导致轴承乌金疲劳损坏。

（2）过大振动将会造成通流部分磨损，严重时将会导致大轴弯曲。

统计数据表明，汽轮发电机组60％以上的大轴弯曲事故就是由于摩擦引起的。

(3）振动过大还将使部件承受大幅交变应力，容易造成转子、联结螺栓、管道、地基等的损坏。

正因为振动对设备安全运行相当重要，人们对振动问题都很重视。

目前大型机组上普遍安装了振动监测系统，并将振动信号投了保护。

振动超标时,保护动作,机组自动停机，从而保证设备的绝对安全。

一、振动分析基本概念振动是一个动态量。

图所示是一种简单的振动形式－简谐振动，即振动量按余弦（或正弦）函数规律周期性地变化，幅值反映了振动大小;频率反映了振动量动态变化的快慢程度；相位反映了信号在t=0时刻的初始状态。

可见，为了完全描述一个振动信号,必须同时知道幅值、频率和相位这三个参数，人们称之为振动分析的三要素。

振动是一个动态变化量。

为了突出反映交变量的影响，振动监测时常取波形中正、负峰值的差值作为振动幅值，又称为峰峰值。

简谐振动是一种简单的振动形式，实际机组上发生的振动比简谐振动要复杂得多.不管振动多么复杂，由信号分析理论可知,都可以将其分解为若干具有不同频率、幅值和相位的简谐分量的合成.旋转机械振动分析离不开转速，为了方便和直观起见，常以1x 表示与转动频率相等的频率，又称为工（基)频；以0。

5x、2x、3x 等表示与转动频率的0.5 倍、2 倍和3 倍等相等的频率，又称为半频、二倍频、三倍频。