第4章 线性回归经典假设的分析

线性回归模型的经典假定及检验、修正一、线性回归模型的基本假定1、一元线性回归模型一元线性回归模型是最简单的计量经济学模型，在模型中只有一个解释变量，其一般形式是Y =β0+β1X 1+μ其中，Y 为被解释变量，X 为解释变量，β0与β1为待估参数，μ为随机干扰项。

回归分析的主要目的是要通过样本回归函数（模型）尽可能准确地估计总体回归函数（模型）。

为保证函数估计量具有良好的性质，通常对模型提出若干基本假设。

假设1：回归模型是正确设定的。

模型的正确设定主要包括两个方面的内容：（1）模型选择了正确的变量，即未遗漏重要变量，也不含无关变量；（2）模型选择了正确的函数形式，即当被解释变量与解释变量间呈现某种函数形式时，我们所设定的总体回归方程恰为该函数形式。

假设2：解释变量X 是确定性变量，而不是随机变量，在重复抽样中取固定值。

这里假定解释变量为非随机的，可以简化对参数估计性质的讨论。

假设3：解释变量X 在所抽取的样本中具有变异性，而且随着样本容量的无限增加，解释变量X 的样本方差趋于一个非零的有限常数，即∑(X i −X ̅)2n i=1n→Q,n →∞ 在以因果关系为基础的回归分析中，往往就是通过解释变量X 的变化来解释被解释变量Y 的变化的，因此，解释变量X 要有足够的变异性。

对其样本方差的极限为非零有限常数的假设，旨在排除时间序列数据出现持续上升或下降的变量作为解释变量，因为这类数据不仅使大样本统计推断变得无效，而且往往产生伪回归问题。

假设4：随机误差项μ具有给定X 条件下的零均值、同方差以及无序列相关性，即E(μi|X i)=0Var(μi|X i)=σ2Cov(μi,μj|X i,X j)=0, i≠j随机误差项μ的条件零均值假设意味着μ的期望不依赖于X的变化而变化，且总为常数零。

该假设表明μ与X不存在任何形式的相关性，因此该假设成立时也往往称X为外生性解释变量随机误差项μ的条件同方差假设意味着μ的方差不依赖于X的变化而变化，且总为常数σ2。

线性回归的前提条件线性回归的前提假设条件是：（1）自变量与因变量是否呈直线关系。

（2）因变量是否符合正态分布。

（3）因变量数值之间是否独立。

（4）方差是否齐性。

其实如果正规地来说，应该是看残差（residual）是否正态、独立以及方差齐。

所谓残差，就是因变量的真实值与估计值之间的差值。

回归分析是一类统计方法，包括本次介绍的线性回归以及后面将要介绍的logistic回归、Cox回归等，该类方法内容十分丰富，在医学应用中也极为广泛。

回归分析主要是通过建立回归方程来说明某一个事物随另一个(或多个)事物的变化而变动的规律。

相关分析研究的是两个或多个变量相互依存变动的规律，见统计分析之相关，而回归分析则是探索某变量(因变量)如何依赖于其他变量(自变量)的变化而变动的规律，是单方依存，而不是相互依存。

回归分析主要根据因变量的类型而划分不同方法，线性回归其因变量必须是定量变量，后面介绍的logistic回归、Cox回归等因变量则属于其他类型。

线性回归可以说是回归家族中最为经典的方法，同时也是相对简单、容易理解的方法。

本系列主要介绍线性回归的应用，具体内容包括：(1)线性回归的单因素分析；(2)线性回归的多因素分析；一、线性回归简介线性回归是研究因变量(dependent variable)与自变量(independent variable)相依关系的技术。

因变量又称应变量(response variable)，是随机变量，具有一个随机分布，依赖于一个或多个自变量。

自变量有时也被称为解释变量(explanatory variable)或预测变量(predictor variable)，是非随机的，不依赖于其他变量。

线性回归中的因变量必须是定量变量，自变量可以是定量变量，也可以是分类变量。

例如研究体重对高血压的影响，体重是自变量，高血压受体重的影响，是因变量。

线性回归大致可分为三类：当因变量有一个，自变量也只有一个时，称之为简单线性回归(simple linear regression)；当因变量有一个，自变量有多个时，称之为多重线性回归(multiple linear regression)；当因变量有多个，自变量有多个时，称之为多元回归(multi-variate regression)。

线性回归经典假设的分析（案例）多重共线性分析财政收入是一个国家政府部门的公共收入。

国家财政收入的规模大小往往是衡量其经济实力的重要标志。

近20年来，我国财政收入一直保持着快速增长态势，经济总体发展良好。

一个国家财政收入的规模要受到经济规模等诸多因素的影响。

因此我们以财政收入为被解释变量，建立财政收入影响因素模型，分析影响财政收入的主要因素及其影响程度。

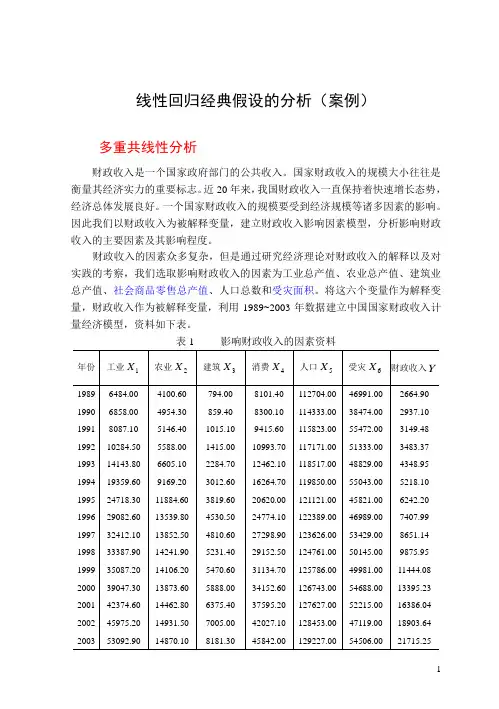
财政收入的因素众多复杂，但是通过研究经济理论对财政收入的解释以及对实践的考察，我们选取影响财政收入的因素为工业总产值、农业总产值、建筑业总产值、社会商品零售总产值、人口总数和受灾面积。

将这六个变量作为解释变量，财政收入作为被解释变量，利用1989~2003年数据建立中国国家财政收入计量经济模型，资料如下表。

表1 影响财政收入的因素资料（资料来源：《中国统计年鉴2004》）使用上述数据建立多元线性模型，采用普通最小二乘法得到国家财政收入估计方程为：1234562(0.46)(0.44)(8.59)(0.03)(3.80)(0.65)( 1.53)6922.5880.1260.9360.0400.5720.0920.0470.998620.56Y X X X X X X R F ---=-+-+++-==由上可以看出模型的拟合优度2R 和F 值都较大，说明建立的回归方程显著。

但在显著性水平为5%下， t (15)=2.131，大多数回归参数的t 检验不显著，若据此判断大部分因素对财政收入的影响不显著。

因此可以判定解释变量之间存在严重的多重共线性。

采用逐步回归法对解释变量进行筛选。

分别将Y 与各解释变量作一元线性回归方程，以拟合优度值最大的模型为基础，将其余变量依次引入方程中。

经过我们多次比较各模型的F 值和各参数的t 值，最终确定的模型为：242(1.79)(13.42)(35.57)519.6780.8120.7230.9971943.91Y X X R F -=-+==该模型的经济意义十分明显，即财政收入主要取决于农业总产值和社会商品零售总产值，各因素数量的变化引起财政收入总量变化的程度由各自的系数来反映。

第四章 经典单方程计量经济学模型：放宽基本假定的模型前两章计量经济学模型的回归基于若干基本假设，应用普通最小二乘法得到了线性、无偏、有效的参数估计量。

但实际的计量经济学问题中，完全满足这些基本假定的情况不多。

称不满足基本假定的情况为基本假定违背。

以一元为例，重述基本假定：① i X 为确定性变量，非随机的（i X 确定，且j X 间互不相关；若多元回归时相关，称为多重共线性：()1rk X k <+； 若存在一个或多个解释变量是随机变量，称为随机解释变量问题）；② 随机干扰项具有0均值，同方差：20,i i D E μμμσ==（2i i D μσ=即所谓异方差）③ cov(,)0,i j i j μμ=∀≠，随机干扰项互相独立，无序列相关（()cov ,0i j μμ≠，序列相关）。

④ ()cov ,0,1,2,...,,1,2,...,ji i X j k i n μ===，解释变量与随机误差项间不相关，这样将j i X ，i μ对Y 的影响分开。

⑤ ()20,,1,2,...,iN i n μμσ=，由中心极限定理保证。

而①―④需要作出计量经济学意义的检验。

基于此，基本假定违背主要包括以下几种情况：1）随机干扰项序列存在异方差性（同方差）；2）随机干扰项序列存在序列相关性（序列不相关）；3）解释变量之间存在多重共线性（不相关）；4）解释变量是随机变量，且与随机干扰项相关（解释变量确定，与随机干扰项不相关）；5）模型设定有偏误（模型设定正确）；6）解释变量的方差随着样本容量的增加而不断增加（方差趋于常值）。

在对计量经济学模型进行回归分析时，必须要进行计量经济学检验：检验是否存在一种或多种违背基本假定的情况。

若有违背情况，应用普通最小二乘法估计模型就不能得到无偏的、有效的参数估计量，OLS法失效，这就需要发展新的方法估计模型。

本章主要讨论前四种，后两种将在第五四章、第九章讨论。

4.1 异方差性（93页）一、异方差性（主要以一元为例，多元类似）1．异方差性概念（Heteroskedasticity）：同方差性是指每个i 围绕其零平均值的方差，并不随解释变量X 的变化而变化，不论解释变量观测值是大还是小，每个i μ的方差保持相同，即 2i const σ=。

线性回归方法线性回归是一种常见的统计学习方法，它用于研究自变量与因变量之间的线性关系。

在实际应用中，线性回归方法被广泛应用于预测、建模和分析数据。

本文将介绍线性回归方法的基本原理、模型建立和评估等内容，希望能够帮助读者更好地理解和运用线性回归方法。

一、线性回归的基本原理。

线性回归方法基于线性模型，假设自变量与因变量之间存在线性关系。

其基本形式可以表示为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε。

其中，Y表示因变量，X1、X2、...、Xn表示自变量，β0、β1、β2、...、βn表示回归系数，ε表示误差项。

线性回归的目标是通过最小化误差项来估计回归系数，从而建立自变量与因变量之间的线性关系模型。

二、线性回归模型的建立。

在建立线性回归模型时，首先需要确定自变量与因变量之间的关系，然后选择合适的变量进行建模。

接着，通过最小二乘法等方法来估计回归系数，最终得到线性回归模型。

在实际应用中，可以利用统计软件进行线性回归模型的建立。

例如，使用R语言、Python等工具可以方便地进行线性回归分析，从而得到回归系数和模型拟合效果等结果。

三、线性回归模型的评估。

在建立线性回归模型后，需要对模型进行评估，以确定模型的拟合效果和预测能力。

常用的评估指标包括R方值、均方误差、残差分析等。

R方值是衡量模型拟合效果的指标，其取值范围在0到1之间，值越接近1表示模型拟合效果越好。

均方误差是衡量模型预测能力的指标，其值越小表示模型的预测能力越强。

残差分析可以帮助检验模型的假设是否成立，进而评估模型的有效性。

四、线性回归方法的应用。

线性回归方法在实际应用中具有广泛的应用价值。

例如，在金融领域，可以利用线性回归方法来预测股票价格的走势；在医学领域，可以利用线性回归方法来研究疾病发展的规律；在市场营销领域，可以利用线性回归方法来分析产品销售数据等。

总之，线性回归方法是一种简单而有效的统计学习方法，它可以帮助我们建立自变量与因变量之间的线性关系模型，从而进行预测、建模和分析数据。

线性回归方法线性回归是一种用于建立自变量和因变量之间关系的统计学方法。

在实际应用中，线性回归通常用于预测和发现变量之间的关联。

它是一种简单而有效的预测模型，被广泛应用于经济学、金融学、生物学、工程学等领域。

首先，我们来了解一下线性回归的基本原理。

线性回归假设自变量和因变量之间存在线性关系，即因变量可以通过自变量的线性组合来表示。

数学上，线性回归模型可以表示为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε。

其中，Y表示因变量，X1、X2、...、Xn表示自变量，β0、β1、β2、...、βn表示模型的参数，ε表示误差项。

线性回归的目标是找到最佳的参数估计，使得模型的预测值与实际观测值之间的误差最小化。

在实际应用中，我们通常使用最小二乘法来估计线性回归模型的参数。

最小二乘法的核心思想是最小化观测值与模型预测值之间的残差平方和，从而得到最优的参数估计。

通过最小二乘法，我们可以得到模型的参数估计值，进而进行预测和推断分析。

除了最小二乘法，线性回归还有一些常见的扩展方法，例如岭回归、Lasso回归和弹性网络回归等。

这些方法在处理多重共线性、过拟合和模型选择等问题上具有一定的优势，可以提高模型的预测能力和解释能力。

在实际应用中，我们需要注意线性回归模型的假设条件和局限性。

线性回归模型假设自变量和因变量之间存在线性关系，并且误差项服从正态分布。

在应用时，我们需要对模型的假设条件进行检验，以确保模型的有效性和可靠性。

此外，线性回归模型也存在一些局限性，例如对异常值和离群点敏感，对非线性关系的拟合能力较弱等。

在实际应用中，我们需要结合具体问题和数据特点，选择合适的模型和方法。

总的来说，线性回归是一种简单而有效的统计方法，被广泛应用于各个领域。

通过对线性回归方法的理解和应用，我们可以更好地理解变量之间的关系，进行预测和推断分析，为决策提供科学依据。

同时，我们也需要注意线性回归模型的假设条件和局限性，以确保模型的有效性和可靠性。

第四章 多元线性回归模型第一节 二元线性回归模型一、二元线性回归模型的设定设二元线性回归模型为： 01122Y X X βββε=+++假设从总体中随机抽取了一个容量为n 的样本，其观测为11121212221212(,,),(,,)(,,)(,,)i i i n n n y x x y x x y x x y x x L L L L ,则模型可以表示为：10111221120112222201122n n n ny x x y x x y x x βββεβββεβββε=+++=+++=+++L L如果令1112110212222121211,,,1n n n n y x x y x x Y X y x x εβεββεβε⎛⎫⎡⎤⎛⎫⎛⎫ ⎪ ⎪⎢⎥ ⎪ ⎪ ⎪⎢⎥==== ⎪ ⎪ ⎪⎢⎥⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭M M M M M则二元线性回归模型可用的矩阵表示为：Y X βε=+关于二元线性回归模型的假设条件，前五条与一元线性回归模型的假定是一致的，由于二元线性回归模型中增加了一个解释变量，所以二元线性回归模型还需增加一个假定，即假定1X 与2X 不存在多重共线性。

二、二元线性回归模型的参数估计假设已经得到参数0β，1β，2β的估计值分别记为0ˆβ，1ˆβ，2ˆβ，则iε的估计值ˆi ε和观测值i y 可以表示为：0112201122垐?ˆˆ(1,2,)垐?ˆ(1,2,)i i i i i ii i i i y y y x x i n y x x i n εββββββε⎧=-=---=⎪⎨=+++=⎪⎩L L L L则根据最小二乘法的思想，要取这样一组0ˆβ，1ˆβ，2ˆβ，使残差平方和最小，即 220112211垐?ˆmin ()n ni i i ii i S y x x εβββ====---∑∑ 为使上式达到最小值，可以对0ˆβ，1ˆβ，2ˆβ求偏导得到： 01122100112211101122212垐?2()(1)0ˆ垐?2()()0ˆ垐?2()()0ˆn i i ii n i i i ii ni i i ii Sy x x S y x x x S y x x x ββββββββββββ===⎧∂=---⨯-=⎪∂⎪⎪∂⎪=---⨯-=⎨∂⎪⎪∂⎪=---⨯-=⎪∂⎩∑∑∑ 由上式可以得到0ˆβ，1ˆβ，2ˆβ的值。

在计量经济学建模实践中，研究者都力所能及的令所创建的模型满足经典线性回归模型的所有基本假定，因为只有这样，该模型的参数估计才具有一系列的优良统计性质，与之相关的各种假设检验才精确可靠，模型总体l来讲也才具有最佳的应用价值，否则，模型将或多或少存在着不足之处，使得其应用性能大打折扣。

为什么计量经济学模型需要这些基本假定呢这些假定又具有什么样的意义呢对于这些最基本的问题，笔者将结合计量经济学的教学实践经验以及对该学科的理解，来对计量经济学经典线性回归模型的基本假定作出通俗的解释。

1.计量经济学模型需要完美性辨证唯物主义告诉我们，不管是什么偶然的现象，其背后都有必然的规律性在起着支配作用，世界是偶然性与必然性的辩证统一。

科学研究的目的，即是在诸多的偶然性现象中发现其不变的必然性，从而推动人类物质文明和精神文明的进步。

计量经济学的研究也不例外，其目的是为了在复杂多变的经济现象中发现其不变的本质，从而获得对特定经济系统的规律性认识，为经济发展与社会进步服务。

计量经济学通过创建数学模型来揭示经济现象的数量规律，从而弥补了以逻辑推理和文字描述为主、缺乏定量分析的经济理论的不足。

以研究商品需求为例，传统的经济学理论“需求定律”只能告诉我们商品需求与价格之间具有反向变动的关系，但无法告诉我们当价格变化一定量时，需求会随之变化多少量，而计量经济学的建模分析则能够把两者之间的定量关系估计出来，这种能力是其他经济学理论所不能替代的。

既然计量经济学建模分析的目的是通过创建适当的数学模型来揭示经济变量之间的数量规律性，那么计量经济学就必须首先要回答这样一个问题一一“我们到底需要一个什么样的计量经济学模型”这个问题的答案是显而易见的，那就是，我们需要一个“尽可能完全揭示经济变量之间的数量规律性”（以下称“第一大完美性特征”）并且“便于进行研究” （以下称“第二大完美性特征”）的计量经济学模型。

这里的“便于进行研究”是指便于进行参数估计和假设检验，并且便于进行数学推导。