实验心理学08-多因素的实验设计

多因素实验设计-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN3多因素组内实验设计多因素组内（被试内）实验设计是单因素组内实验设计的扩展。

在多因素被试内实验设计中，基本方法是：随机取样被试，参加实验的被试接受全部实验处理水平的结合。

以两因素被试内实验设计举例，表2中自变量A因素有两个水平，B 因素有四个水平。

两个因素共有2×4=8种处理水平的结合，即A1B1，A1B2，A1B3，A1B4，A2B1，A2B2，A2B3，A2B4。

参加实验的每个被试接受所有自变量实验处理水平的结合。

实验设计的基本思想是，由于每个被试接受所有的试验处理水平的结合，因而实验处理后测量到的差异应当来自A因素、B因素，或来自A因素与B因素的交互作用。

表2 两因素被试内实验设计举例4混合实验设计在多因素实验设计中，当两个或多个因素均为被试间因素时，我们称之为组间或被试间实验设计，当两个或多个因素均为被试内因素时，我们称之为组内或被试内实验设计。

然而，还有一种可能性，多因素实验设计中的自变量既包含有被试间因素，又包含有被试内因素，这种情况我们称之为混合实验设计（Mixed Factorial Design）。

混合实验设计的基本方法是，首先确定实验中的被试间因素和被试内因素，将被试按被试间因素的水平数随机分组，然后，每组被试接受被试间因素的某一处理水平与被试内因素所有处理水平的结合。

我们仍以两因素混合实6解决多变量实验设计缺点的方法一种常用的方法是在确认分解的各因素之间不存在交互作用的前提下，将复杂的多变量实验设计分解为若干个单因素和简单的多因素实验设计，分多次实施实验，然后再将多个实验获得的数据放到一起进行分析和讨论，这样就减少了由于实验设计的复杂给主试和实验者实施实验带来的困难，提高了实验者对实验过程的可控性。

多因素实验设计
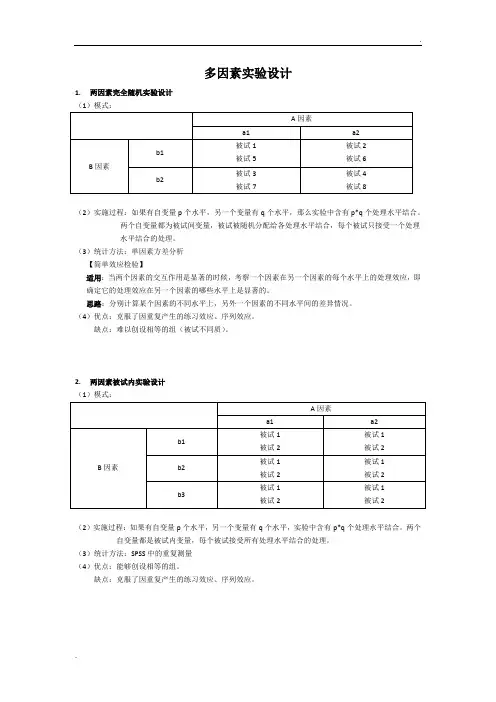
1.两因素完全随机实验设计
（1）模式：
（2）实施过程：如果有自变量p个水平，另一个变量有q个水平，那么实验中含有p*q个处理水平结合。

两个自变量都为被试间变量，被试被随机分配给各处理水平结合，每个被试只接受一个处理
水平结合的处理。

（3）统计方法：单因素方差分析
【简单效应检验】
适用：当两个因素的交互作用是显著的时候，考察一个因素在另一个因素的每个水平上的处理效应，即确定它的处理效应在另一个因素的哪些水平上是显著的。

思路：分别计算某个因素的不同水平上，另外一个因素的不同水平间的差异情况。

（4）优点：克服了因重复产生的练习效应、序列效应。

缺点：难以创设相等的组（被试不同质）。

2.两因素被试内实验设计
（1）模式：
（2）实施过程：如果有自变量p个水平，另一个变量有q个水平，实验中含有p*q个处理水平结合。

两个自变量都是被试内变量，每个被试接受所有处理水平结合的处理。

（3）统计方法：SPSS中的重复测量
（4）优点：能够创设相等的组。

缺点：克服了因重复产生的练习效应、序列效应。

3.两因素混合实验设计
（1）模式：
（2）实施过程：如果有自变量p个水平，另一个变量有q个水平，实验中含有p*q个处理水平结合。

两个变量中一个是被试内变量，另一个是被试间变量。

（3）统计方法：SPSS中的重复测量
（4）优点：有效的控制额外变量，更有利于揭示变量间的因果关系。

缺点：操作繁杂，费时费力。

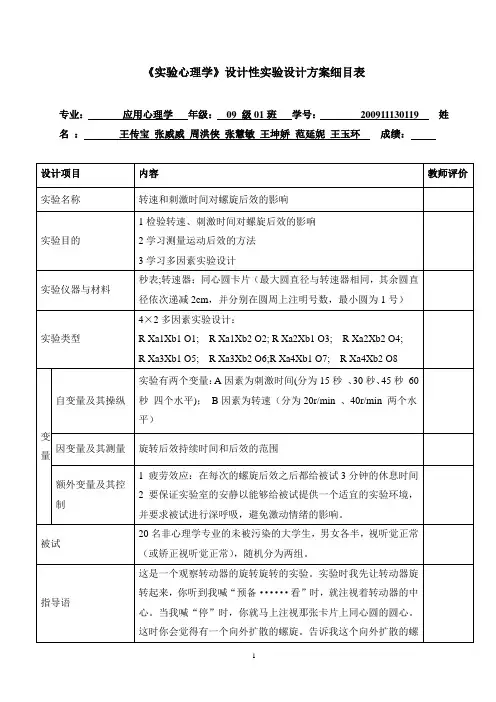
《实验心理学》设计性实验设计方案细目表专业：应用心理学年级：09 级01班学号：200911130119 姓名：王传宝张威威周洪侠张慧敏王坤娇范延妮王玉环成绩：设计项目内容教师评价实验名称转速和刺激时间对螺旋后效的影响实验目的1检验转速、刺激时间对螺旋后效的影响2学习测量运动后效的方法3学习多因素实验设计实验仪器与材料秒表;转速器；同心圆卡片（最大圆直径与转速器相同，其余圆直径依次递减2cm，并分别在圆周上注明号数，最小圆为1号）实验类型4×2多因素实验设计：R Xa1Xb1 O1; R Xa1Xb2 O2; R Xa2Xb1 O3; R Xa2Xb2 O4; R Xa3Xb1 O5; R Xa3Xb2 O6;R Xa4Xb1 O7; R Xa4Xb2 O8变量自变量及其操纵实验有两个变量：A因素为刺激时间(分为15秒、30秒、45秒60秒四个水平)；B因素为转速（分为20r/min 、40r/min 两个水平）因变量及其测量旋转后效持续时间和后效的范围额外变量及其控制1 疲劳效应：在每次的螺旋后效之后都给被试3分钟的休息时间2 要保证实验室的安静以能够给被试提供一个适宜的实验环境，并要求被试进行深呼吸，避免激动情绪的影响。

被试20名非心理学专业的未被污染的大学生，男女各半，视听觉正常（或矫正视听觉正常），随机分为两组。

指导语这是一个观察转动器的旋转旋转的实验。

实验时我先让转动器旋转起来，你听到我喊“预备······看”时，就注视着转动器的中心。

当我喊“停”时，你就马上注视那张卡片上同心圆的圆心。

这时你会觉得有一个向外扩散的螺旋。

告诉我这个向外扩散的螺旋的最大范围和第几号圆一样大。

等你再也看不到扩散现象的时候就立即告诉我。

现在咱们可以先做两次。

你要注意掌握扩散范围的标准，以及扩散现象停止的标准，这种标准在整个实验中要前后一致。

多因素实验设计方法
《多因素实验设计方法》
嘿，你知道吗？多因素实验设计方法可有意思啦！这就像是一个神奇的魔法盒，能让我们发现好多隐藏的秘密呢。

想象一下，我们面对一个复杂的问题，就好像走进了一个迷宫。

单因素实验就像是只沿着一条路走，可能会错过很多其他的精彩。

但多因素实验设计呢，就不一样啦！它就像是同时打开了好多条路，让我们能更全面地去探索这个迷宫。

比如说，我们想研究一种药物的效果。

光看剂量这一个因素可不行呀，还得考虑患者的年龄、性别、身体状况等等好多方面呢。

多因素实验设计就能把这些都考虑进去，让我们得到更准确、更有价值的结果。

而且哦，它还特别灵活。

我们可以根据具体的需求，自由地选择要研究的因素，还可以调整每个因素的水平。

就像是搭积木一样，我们可以搭出各种不同的形状，来满足我们不同的研究目的。

在进行多因素实验设计的时候，可得精心策划。

要想好每个因素怎么设置，怎么去收集数据，怎么分析结果。

这就像是导演一场大戏，每个环节都不能马虎。

多因素实验设计方法真的是超级实用，能让我们更深入地了解事物之间的关系，发现那些不容易被注意到的规律。

它就像是一把钥匙，能打开知识宝库的大门，让我们看到更多的精彩。

心理学多因素实验设计案例案例：不同音乐类型和学习环境对记忆效果的影响。

一、实验目的。

咱就想知道啊，听着不同类型的音乐，然后在不同的学习环境里，到底对记忆东西有啥不一样的影响呢？是能让我们像超级学霸一样过目不忘，还是变得像金鱼一样只有七秒记忆呢 。

二、实验因素和水平。

1. 音乐类型（因素A）水平一：古典音乐，就像莫扎特、贝多芬那些高大上的曲子，感觉一听就很有文化气息 。

水平二：流行音乐，周杰伦啊、泰勒·斯威夫特之类的，超级抓耳，大街小巷都在放的那种。

水平三：摇滚音乐，比如崔健、AC/DC，充满激情，让你听了就忍不住想摇头晃脑的那种。

2. 学习环境（因素B）水平一：安静的图书馆环境，超安静，只有翻书的沙沙声和偶尔的咳嗽声。

水平二：稍微有点嘈杂的咖啡店环境，有咖啡机的嗡嗡声，人们的低声交谈声。

水平三：家庭环境，可能会有电视的背景音，家人偶尔走动的声音。

三、实验设计类型。

我们采用3×3的完全随机多因素实验设计。

也就是说，我们要把这音乐类型的三个水平和学习环境的三个水平进行各种组合，然后随机分配给不同的参与者。

四、实验对象。

找了90个大学生，为啥是大学生呢？因为他们学习任务多，而且好忽悠……不是，是因为他们比较容易找到，而且处于经常需要记忆知识的阶段 。

五、实验过程。

1. 先把这90个大学生随机分成9组，每组10个人。

2. 对于第一组，让他们戴着耳机听古典音乐，然后坐在模拟图书馆的安静环境里，给他们一篇文章看15分钟，然后把文章拿走，让他们尽可能地回忆文章里的内容，记录下他们能回忆起来的字数。

3. 第二组呢，同样听古典音乐，但是是在模拟咖啡店的嘈杂环境里做同样的事情，记录回忆字数。

4. 第三组听古典音乐，在模拟家庭环境里进行，然后记录。

5. 第四组换成流行音乐，按照上面三种环境分别进行实验，记录回忆字数。

6. 第五组听摇滚音乐，也在三种环境下依次做实验，记录结果。

六、可能的结果和解释。

第1篇一、实验目的本研究旨在探讨多因素实验设计在心理学领域中的应用，通过实验验证不同自变量对因变量的影响，并分析自变量之间的交互作用。

本实验选取了两个自变量：实验组别和实验时长，考察其对被试反应时间的影响。

二、实验方法1. 实验对象实验对象为30名大学生，男女各半，年龄在18-22岁之间。

所有被试均无色盲、色弱等视觉障碍。

2. 实验材料实验材料为一系列图片，每张图片包含一个字母，要求被试在看到图片后尽快判断该字母是否为目标字母。

3. 实验设计本实验采用2（实验组别：实验组与对照组）×2（实验时长：短时长与长时长）的多因素实验设计。

其中，实验组别为自变量A，实验时长为自变量B。

4. 实验程序（1）实验前，向被试说明实验目的和实验流程，并要求被试在实验过程中保持专注。

（2）实验过程中，将30名被试随机分为两组，每组15人。

实验组进行短时长实验，对照组进行长时长实验。

（3）短时长实验：实验组被试在30秒内完成所有图片判断任务。

（4）长时长实验：对照组被试在60秒内完成所有图片判断任务。

（5）实验结束后，收集被试的反应时间数据。

5. 数据处理采用SPSS软件对实验数据进行方差分析，以检验自变量A和B对因变量（反应时间）的影响，以及自变量之间的交互作用。

三、实验结果1. 实验组别对反应时间的影响方差分析结果显示，实验组别对反应时间有显著影响（F(1,28) = 8.71，p <0.01）。

具体来说，实验组被试的平均反应时间为523.71毫秒，对照组被试的平均反应时间为598.43毫秒。

2. 实验时长对反应时间的影响方差分析结果显示，实验时长对反应时间有显著影响（F(1,28) = 6.82，p <0.05）。

具体来说，短时长实验组被试的平均反应时间为523.71毫秒，长时长实验组被试的平均反应时间为598.43毫秒。

3. 自变量之间的交互作用方差分析结果显示，实验组别与实验时长之间存在交互作用（F(1,28) = 5.05，p < 0.05）。

多变量实验设计在心理学实验设计中，一类实验设计是考察单一自变量（或称为因素）对因变量的影响，这类实验设计称为单变量实验设计（Single-Variable Experiment）；另外一类实验设计是考察两个或两个以上的自变量（或因素）对因变量的影响，这类实验设计称为多变量试验设计（Multiple-Variable Experiment）。

多变量实验设计包括多因素组间实验设计、多因素组内实验设计和混合实验设计。

2多因素组间实验设计多因素组间实验设计是单因素组间实验设计的扩展。

在多因素完全随机实验设计中，基本方法是：随机取样被试，并将参加实验的被试分为若干个实验处理组，每组被试分别接受一种实验处理水平的结合。

我们以两因素完全随机实验设计举例，表1中自变量A因素有两个水平，B因素有四个水平。

两个因素共有2×4=8种处理水平的结合，即A1B1，A1B2，A1B3，A1B4，A2B1，A2B2，A2B3，A2B4。

将被试随机分为八组，每组被试接受一个自变量实验处理水平的结合。

实验设计的基本思想是，由于实验处理前，被试是随机分配给各实验处理组的，因而保证了各组被试实验之前无差异。

实验处理后测量到的差异可能来自A因素、B因素，或来自A因素与B因素的交互作用。

表1 两因素完全随机实验设计举例实验处理水平的结合后测实验组1 A1B1 Y实验组2 A1B2 Y实验组3 A1B3 Y实验组4 A1B4 Y实验组5 A2B1 Y实验组6 A2B2 Y实验组7 A2B3 Y实验组8 A2B4 Y3多因素组内实验设计多因素组内（被试内）实验设计是单因素组内实验设计的扩展。

在多因素被试内实验设计中，基本方法是：随机取样被试，参加实验的被试接受全部实验处理水平的结合。

以两因素被试内实验设计举例，表2中自变量A因素有两个水平，B因素有四个水平。

两个因素共有2×4=8种处理水平的结合，即A1B1，A1B2，A1B3，A1B4，A2B1，A2B2，A2B3，A2B4。

多因素实验设计因素分解交互作用的数量：KCn=K！/n(K-n)！K：因素（自变量）的数量；n：交互作用的次数1 单因素实验设计1.1 单因素完全随机实验设计：分解：SS总变异=SS组间+SS组内计算：SS总变异=[AS]-[Y] df=np-1SS组间=[A]-[Y] df=p-1SS组内= SS总变异-SS组间df=p(n-1)1.2 单因素随机区组实验设计分解：SS总变异=SS处理间+SS处理内=SSA+（SS区组+SS残差）计算：SS总变异=[AS]-[Y] df=np-1SSA=[A]-[Y] df=p-1SS处理内=SS总变异-SS处理间SS区组=[S]-[Y] df=n-1SS残差=SS总变异-SSA-SS区组df=(n-1)(p-1)1.3 单因素拉丁方实验设计分解：SS总变异=SS处理间+SS处理内=SSA+（SSB+SSC+SS单元内+SS残差）计算：SS总变异=[ABCS]-[Y] df=np-1SSA=[A]-[Y] df=p-1SSB=[B]-[Y] df=p-1SSC=[C]-[Y] df=p-1SS单元内=[ABCS]-[ABC] df=p2(n-1)SS残差={[ABC]-[Y]}-SSA-SSB-SSC df=(n-1)(p-2)1.4 单因素重复测量实验设计分解：SS总变异=SS被试间+SS被试内=SS被试间+（SSA+SS残差）计算：SS总变异=[AS]-[Y] df=np-1SS被试间=[S]-[Y] df=n-1SS被试内=SS总变异-SS被试间SSA=[A]-[Y] df=p-1SS残差= SS总变异-SS被试间-SSA df=(n-1)(p-1)2 两因素实验设计2.1 两因素完全随机实验设计分解：SS总变异=SS处理间+SS处理内=（SSA+SSB+SSAB）+SS单元内计算：SS总变异=[ABS]-[Y] df=npq-1SSA=[A]-[Y] df=p-1SSB=[B]-[Y] df=q-1SSAB=[AB]-[Y]-SSA-SSB df=(p-1)(q-1)SS单元内=SS总变异-SSA-SSB-SSABdf=pq(n-1)同质性检验：F=max（SS1组，SS2组，SS3组…SSn组）\min（SS1组，SS2组，SS3组…SSn组）2.2 两因素随机区组实验设计分解：SS总变异=SS处理间+SS处理内=（SSA+SSB+SSAB）+（SS区组+SS残差）计算：SS总变异=[ABS]-[Y] df=npq-1SS区组=[S]-[Y] df=n-1SS处理间=[AB]-[Y]SSA=[A]-[Y] df=p-1SSB=[B]-[Y] df=q-1SSAB=[AB]-[Y]-SSA-SSB df=(p-1)(q-1)SS处理内=SS总变异-SS处理间SS残差=SS总变异-SSA-SSB-SSABdf=(pq-1)(n-1)2.3 两因素混合实验设计分解：SS总变异=SS被试间+SS被试内=（SSA+SS被试A）+（SSB+SSAB +SSB×被试A）计算：SS总变异=[ABS]-[Y] df=npq-1SS被试间=[AS]-[Y]SSA=[A]-[Y] df=p-1SS被试A=SS被试间-SSA df=p(n-1)SS被试内=SS总变异-SS被试间SSB=[B]-[Y] df=q-1SSAB=[AB]-[Y]-SSA-SSB df=(p-1)(q-1)SS B×被试A=SS被试内-SSB-SSABdf=p(q-1)(n-1)2.4 两因素重复测量实验设计分解：SS总变异=SS被试间+SS被试内=SS被试间+（SSA+SS A×被试+SSB+SSB×被试+SSAB+SSA×B×被试）计算：SS总变异=[ABS]-[Y] df=npq-1SS被试间=[S]-[Y] df=n-1SS被试内=SS总变异-SS被试间SSA=[A]-[Y] df=p-1SSA×被试=[AS]-[Y]-SS被试间-SSA df=(p-1)(n-1)SSB=[B]-[Y] df=q-1SSAB=[AB]-[Y]-SSA-SSB df=(p-1)(q-1)SSB×被试=[BS]-[Y]-SS被试间-SSBdf=(q-1)(n-1)SSA×B×被试=SS被试内-SSA-SSA×被试-SSB-SSB×被试-SSAB df=(n-1)(p-1)(q-1)3 三因素实验设计3.1 三因素完全随机实验设计分解：SS总变异=SS处理间+SS处理内=（SSA+SSB+SSC+SSAB+SSAC+SSBC+SSABC）+SS单元内计算：SS总变异=[ABCS]-[Y] df=npqr-1SSA=[A]-[Y] df=p-1SSB=[B]-[Y] df=q-1SSC=[C]-[Y] df=r-1SSAB=[AB]-[Y] df=(p-1)(q-1)SSAC=[AC]-[Y] df=(p-1)(r-1)SSBC=[BC]-[Y] df=(q-1)(r-1)SSABC=[ABC]-[Y]-SSA-SSB-SSC-SSAB-SSAC-SSBC df=(p-1)(q-1)(r-1)SS单元内=SS总变异-SSA-SSB-SSC-SSAB-SSAC-SSBC-SSABC df=pqr(n-1)3.2 三因素混合实验设计3.2.1 重复测量一个因素分解：SS总变异=SS被试间+SS被试内=（SSA+SSC+SSAC+SS被试(AC)）+（SSB+SSAB+SSBC+SSABC+SSB×被试(AC)）计算：SS总变异=[ABCS]-[Y] df=npqr-1SS被试间=[ACS]-[Y] df=npr(q-1)SSA=[A]-[Y] df=p-1SSC=[C]-[Y] df=r-1SSAC=[AC]-[Y] df=(p-1)(r-1)SS被试(AC)=SS被试间-SSA-SSC-SSAC df=pr(n-1)SS被试内=SS总变异-SS被试间SSB=[B]-[Y] df=q-1SSAB=[AB]-[Y] df=(p-1)(q-1)SSBC=[BC]-[Y] df=(q-1)(r-1)SSABC=[ABC]-[Y]-SSA-SSB-SSC-SSAB-SSAC-SSBC df=(p-1)(q-1)(r-1)SSB×被试(AC)=SS被试内-SSB-SSAB-SSBC-SSABC df=pr(n-1)(q-1)3.2.2 重复测量两个因素分解：SS总变异=SS被试间+SS被试内=（SSA+SS被试(A)）+（SSB+SSAB+SSB×被试(A)+SSC+SSAC+ SSC×被试(A)+SSBC+SSABC+SSB×C×被试(A)）计算：SS总变异=[ABCS]-[Y] df=npqr-1SS被试间=[AS]-[Y] df=np-1SSA=[A]-[Y] df=p-1SS被试(A)=SS被试间-SSA df=p(n-1)SS被试内=SS总变异-SS被试间SSB=[B]-[Y] df=q-1SSAB=[AB]-[Y]-SSA-SSB df=(p-1)(q-1)SSB×被试(A)=[ABS]-[Y]-SS被试间-SSB-SSAB df=p(n-1)(q-1)SSC=[C]-[Y] df=r-1SSAC=[AC]-[Y]-SSA-SSC df=(p-1)(r-1)SSC×被试(A)=[ACS]-[Y]-SS被试间-SSC-SSAC df=p(n-1)(r-1)SSBC=[BC]-[Y]-SSB-SSC df=(q-1)(r-1)SSABC=[ABCS]-[Y]-SSA-SSB-SSAB-SSAC-SSBC df=df=(p-1)(q-1)(r-1)SSB×C×被试(A)=SS被试内-SSB-SSAB-SSB×被试(A)-SSC-SSAC-SSC×被试(A)-SSBC-SSABC 4三因素重复测量实验设计分解：SS总变异=SS被试间+SS被试内=SS被试间+（SSA+SSA×被试+SSB+SSB×被试+SSC+SSC×被试+SSAB+SSA×B×被试+SSAC+SSA×C×被试+SSBC+SSB×C×被试+SSABC+SS A×B×C×被试）计算：SS总变异=[ABCS]-[Y] df=npqr-1SS被试间=[S]-[Y] df=n-1SS被试内=SS总变异-SS被试间SSA=[A]-[Y] df=p-1SSA×被试=[AS]-[Y]-SS被试间-SSA df=(p-1)(n-1)SSB=[B]-[Y] df=q-1SSB×被试=[BS]-[Y]-SS被试间-SSB df=(q-1)(n-1)SSC=[C]-[Y] df=r-1SSC×被试=[CS]-[Y]-SS被试间-SSC df=(r-1)(n-1)SSAB=[AB]-[Y]-SSA-SSB df=(p-1)(q-1)SSA×B×被试=[ABS]-[Y]-SS被试间-SSA-SSB-SSAB-SSA×被试-SSB×被试df=(p-1)(q-1)(n-1)SSAC=[AC]-[Y]-SSA-SSC df=(p-1)(r-1)SSA×C×被试=[ACS]-[Y]-SS被试间-SSA-SSC-SSAC-SSA×被试-SSC×被试df=(p-1)(r-1)(n-1) SSBC=[BC]-[Y]-SSB-SSC df=(q-1)(r-1)SSB×C×被试=[BCS]-[Y]-SS被试间-SSB-SSC-SSBC-SSB×被试-SSC×被试df=(q-1)(r-1)(n-1) SSABC=[ABC]-[Y]-SSA-SSB-SSAB-SSAC-SSBC df=df=(p-1)(q-1)(r-1)SS A×B×C×被试=SS被试内-SSA-SSA×被试-SSB-SSB×被试-SSC-SSC×被试-SSAB-SSA×B×被试-SSAC-SSA×C×被试-SSBC-SSB×C×被试-SSABC-SSA×B×C×被试5 嵌套实验设计5.1 两因素完全随机嵌套实验设计5.2 三因素完全随机嵌套实验设计。

心理学实验设计中的多因素分析方法研究心理学实验设计是探究和验证心理学现象的重要手段，可对测试和组织数据进行分析，以帮助心理学家理解各种心理现象和行为。

不同的因素可能会影响实验结果，因此多因素分析方法在实验设计中扮演着关键的角色。

本文旨在探讨心理学实验设计中的多因素分析方法。

一、什么是多因素分析？多因素分析是一种不同因素引起不同效应的分析方法，也被称为方差分析。

多因素分析可以比较不同因素对实验变量的影响，以确定哪个因素是最有影响力的。

二、多因素分析的应用心理学实验通常涉及多个因素，例如，实验参与者的不同年龄，性别，文化和词汇水平等。

为了识别这些影响因素和确定它们的影响程度，心理学家利用多因素分析方法。

多因素分析技术还用于比较不同的实验条件，例如，比较不同的任务类型，任务难度和任务时限。

三、两个因素模型的多因素分析法两个因素模型是心理学研究中最常见的多因素分析。

它有两个因素，也被称为“两个变量模型”。

每个因素都有两个或多个水平，例如，一个实验中可能会比较男性和女性之间的差异，或者比较两组不同的药物疗法。

这两个因素的影响可以单独或同时进行分析，来确定对结果产生更显著影响的因素。

这种设计可以通过单双向多因素方差分析进一步分析。

四、多个因素的多因素分析在心理学领域，多因素分析通常涉及许多不同的因素。

这些因素可以分为连续变量和分类变量。

连续变量指的是类似体重、IQ和血压这样可计量的指标，而分类变量则是通过分类法描述的变量，如性别、年龄、民族等。

多个因素的多因素分析也可以采用单方差分析或双方差分析等方法，并且常常借助于图形和统计表来表示结果，以更加清楚直观。

五、多因素分析的优点和局限性多因素分析方法有以下优点：1. 它可以确定哪个因素对实验变量的影响最大。

2. 它可以分析多个因素之间的交互作用。

3. 它可以提供异常情况发现和纠正技术，以确保实验结果的准确性。

尽管多因素分析方法具有许多优点，但它也存在以下局限性：1. 实验设计复杂，也需要推迟到实验分析阶段才能设计。

1第二节 多因素完全随机实验设计对于单因素完全随机实验设计来说，实验的处理数就是自变量的水平数，将被试随机分配到各个处理组上就可以了。

多因素完全随机实验设计则是多个因素的多种水平相互结合，构成多个处理的结合，如二因素二水平，就是有两个自变量，每个自变量有两个水平，则处理的结合共有四个，这种实验设计称为是2×2实验设计；如果一个自变量两个水平，另一个变量是三个水平，则共有6个实验处理，这种实验设计就是2×3实验设计。

如果有三个自变量，其中两个自变量是2个水平，另一个变量有3个水平，则这种实验设计有12个实验处理，叫做2×2×3设计。

这里需要重申以下几点：第一，自变量是研究者操纵的变量，在实验过程中必须是变化了的，也就是说自变量的水平数至少为2。

如果自变量的水平数为1，那就等于说该变量在实验过程中始终保持在一个水平上，它就不是“变”量了。

比方说，一个2×3×1×2实验设计中，实际上只有三个自变量，它们的水平数分别为2、3、2。

第二，实验处理就是自变量在各种水平上结合而成的各种实验条件，实验处理数等于所有自变量水平数的乘积。

如一个2×3×3实验设计，其实验处理数是18，等于说这一实验过程中出现18种实验条件。

第三，对于完全随机实验设计来说，有多少种实验处理就要有多少组实验被试，因为一组被试只参加一种实验条件下的实验。

现在，我们以下面这个假想的实验研究为例来说明多因素完全随机实验设计的模式。

假设某研究者想考察缪勒错觉受箭头方向和箭头张开角度的影响。

研究中的自变量有两个，一个是箭头方向（标记为A ），分为向内和向外两个水平；另一个是箭头张开角度（标记为B ），设置为15度和45度两个水平，因此这是一个2×2实验设计，构成了4种实验处理，如表2-1所示。

研究者从某大学文学院本科二年级一60人的班级随机抽取了20名男生，再将20名男生随机分成相等的四个组，每组5人，每一个组接受一种实验处理，所以，这是一个二因素完全随机实验设计。

心理学与教育研究中的多因素实验设计——舒华第二章几种基本的实验设计第一节单因素完全随机实验设计一、基本特点适用于：研究中有一个自变量，自变量有两个或多于两个水平。

方法：把被试随机分配给自变量的各个水平，每个水平被试只接受一个水平的处理。

二、计算与举例（一）检验的问题与实验设计（二）实验数据及其计算第二节单因素随机区组实验设计一、基本特点适用于：研究中有一个变量，自变量有两个或多个水平（P≥2），研究中还有一个无关变量，也有两个或多个水平（n≥2）；并且自变量的水平与无关变量的水平之间没有交互作用。

适合检验的假说：（1）处理水平的总体平均数相等或处理效应为零；（2）区组的总体平均数相等或区组效应为零。

二、计算三、优点：从实验中分离出了一个无关变量的效应，从而减少了实验误差。

第三节单因素拉丁方设计一、基本特点定义：是一个含P行、P列、把P个字母分配给方格的管理方案，其中每个字母在每行中只出现一次。

适用于：（1）研究中自变量与无关变量的水平平均≥2，一个无关变量的水平被分配给P行，另一个则给P列；（2）假定处理水平与无关变量水平之间没有交互作用，（3）随即分配处理水平给个方格单元，每个处理水平仅在每行，每列中出现一次。

无关变量C的四个水平无关变量B的四个水平自变量A的四个水平第四节单因素重复测量实验设计一、基本特点：（也叫被试内设计）基本方法：实验中每个被试接受所有的处理水平目的：利用被试自己做控制，使被试的各方面特点在所有的处理中保持恒定，以最大限度地控制由被试的个体差异带来的变异。

假设：当若干处理水平连续实施给同一被试时，被试接受前面的处理，对接受后面的处理没有长期的影响。

优点：从总变异中分离出了被试间变异，与完全随机实验相比，它提高了实验处理的F检验的敏感性。

第三章两因素完全随机和随机区组实验设计第一节两因素完全随机实验设计一、基本特点与单因素相比：可对两个或多个变量之间的交互作用进行估价不同：每个被试接受的是一个处理的结合，而不是一个处理水平二、举例第二节对交互作用的进一步检验一、交互作用图解二、简单效应检验（一）简单效应的基本特点及其作用分别检验一个因素在另一个因素的每个水平上的处理效应，以便具体地确定它的处理效应在另一个因素的哪个水平上是显著的，在哪些水平上是不显著的。