18 过滤过程计算

180000吨/天D型滤池设计计算一、已知条件设计水量：Q=180000m3/d滤池规格：共有14格，每格28㎡，分2组，每组7格。

反冲洗流程：第一阶段：单独气冲，冲洗历时3～5 min，气洗强度23L/（m2·s）；第二阶段：气水同时反冲洗，历时8～10 min，气洗强度23L/（m2·s），水冲洗强度6L/（m2·s）；第三阶段：清水漂洗，冲洗历时3～5 min，冲洗强度6（L/m2·s）；反冲洗全过程中伴有表面扫洗，表面扫洗强度2.8 L/m2·s；冲洗时间共计t=15～20min，冲洗周期T=24h。

（取20min=1/3h）二、设计计算1、池体设计（1）、滤速：v=Q/（F×24）F——滤池总面积，14×28=392㎡v=180000/（392×24）=19.1m/h（2）、校核强制滤速v’v’=Nv/(N－1)=7×19.1/(7－1)=22.3m/h＜23m/h（3）、滤池高度的确定滤板下布水区高度H1=0.9m滤板高度H2=0.03 m滤网板（承托层）高度H3=0.07 m滤网板与注塑盖板之间高度H4=1.9 mV型槽与注塑盖板之间距离为H5=0.1 mV型槽高度为H6=0.635 mV型槽顶至滤池顶高度为H7=0.965 m则滤池总高H= H1 +H2+ H3+H4 +H5+ H6+ H7=0.9+0.03+0.07+1.9+0.1+0.635+0.965=4.6 m（4）、水封池的设计按照试验数据，DA863彗星式纤维滤料清洁滤层的水头损失取ΔH=0.4 m清正常过滤时，通过长柄滤头的水头损失ΔH≤0.22 m，取0.2 m。

忽略其他水头损失，则每次反冲洗后刚开始过滤的水头损失为：=0.4+0.2=0.6mΔH开始为保证滤池正常时滤池内的液面高出滤料层，水封井出水堰顶标高与滤料层相同。

堰底板与滤池底版标高相同，水封井出水堰总高= H1 +H2+ H3=0.9+0.1+0.8=1.8 m。

板框过滤实验报告————————————————————————————————作者：————————————————————————————————日期：实验五 过滤实验1 实验目的1.1 了解板框过滤机的构造、流程和操作方法。

1.2 测定某一压力下过滤分内工程中的过滤常熟K 、q e 、τe 值，增进对过滤理论的理解。

1.3 测定洗涤速率与最终过滤速率间的关系。

2 实验原理2.1 过滤是以某种多孔物质为介质，在外力的作用下，使悬浮液中的连续相液体通过介质的孔道，分散相固体颗粒被截留在介质上，从而实现固/液分离的操作。

液体通过过滤介质和滤饼空隙的流动是流体经过固定床流动的一种具体情况，但过滤操作中的床层厚度不断增加，在一定压差下，滤液通过床层的速率随过滤时间的延长而减小，即过滤操作不属于定态过程。

在恒压过滤时，由于滤饼的增厚，过滤速率将随过滤时间的增加而降低。

对滤饼的洗涤过程，由于滤饼厚度不再增加，压差与速率的关系与固定床相同。

恒压过滤方程：()()sV ssm K m A m V m V KA V V e e e e e 的过滤时间，相当于得到滤液：过滤时间，：过滤常数，：过滤面积，即虚拟滤液体积，滤渣时得到的滤液量，：形成滤布阻力的一层时间内获得的滤液量，：在:/223322τττττ+=+上式两边除以A 2得()()23232//,m m AVq m m A V q K q q e e e e 量滤液量，，单位过滤面积上的当，单位过滤面积的滤液量==+=+ττ2.2 测定K 、q e 、τe ：测与一系列的△τ、△q 值，然后以△τ/△q 为纵坐标，以q 为横坐标作图，即可以得到一条斜率为K 2，截距为q K2的直线，则可以算出K 、q e 的值；再以q=0,τ=0代入式子()()e e K q q ττ+=+2，便可以求出τe。

2.3 测定洗涤速率与最终过滤速率 洗涤速率：sm V V d dV w w ww w 洗涤时间，洗液量，::3τττ=⎪⎭⎫⎝⎛最终过滤速率：()()2332/:22m m q m V q q K V V KA d dV e e E 总量，位过滤面积所得的滤液整个过滤时间内通过单的滤液总量，：整个过滤时间内所得+=+=⎪⎭⎫⎝⎛τ3 实验流程图1 实验装置流程图1－空气压缩机；2－配浆槽；3－压力表；4－贮浆罐；5－洗水罐；6－板框压滤机；7－计量桶；8－压缩空气进气阀；9－空气过滤减压阀；10－进浆阀；11、12－压缩空气进口阀；13－进水阀；14－安全阀；15－洗水进口阀；16－滤浆进口阀；17－滤液出口阀；18－滤浆出口阀8 3 9 4 14 × ×× 6 13 17× ×4 实验步骤4.1 将碳酸镁在储浆槽中加水配制成5.3％的悬浮液作滤浆，并在启动空压机前不停地搅拌，防止固体沉淀；4.2 按板、框的钮数为1－2－3－2－1－2－3－2－1的顺序排列号板框过滤机。

实验五 过滤实验1 实验目的了解板框过滤机的构造、流程和操作方法。

测定某一压力下过滤分内工程中的过滤常熟K 、q e 、τe 值，增进对过滤理论的理解。

测定洗涤速率与最终过滤速率间的关系。

2 实验原理过滤是以某种多孔物质为介质，在外力的作用下，使悬浮液中的连续相液体通过介质的孔道，分散相固体颗粒被截留在介质上，从而实现固/液分离的操作。

液体通过过滤介质和滤饼空隙的流动是流体经过固定床流动的一种具体情况，但过滤操作中的床层厚度不断增加，在一定压差下，滤液通过床层的速率随过滤时间的延长而减小，即过滤操作不属于定态过程。

在恒压过滤时，由于滤饼的增厚，过滤速率将随过滤时间的增加而降低。

对滤饼的洗涤过程，由于滤饼厚度不再增加，压差与速率的关系与固定床相同。

恒压过滤方程： 上式两边除以A 2得 测定K 、q e 、τe ：测与一系列的△τ、△q 值，然后以△τ/△q 为纵坐标，以q 为横坐标作图，即可以得到一条斜率为K 2，截距为q K2的直线，则可以算出K 、q e 的值；再以q=0,τ=0代入式子()()e e K q q ττ+=+2，便可以求出τe。

测定洗涤速率与最终过滤速率 洗涤速率： 最终过滤速率：3 实验流程4 实验步骤将碳酸镁在储浆槽中加水配制成％的悬浮液作滤浆，并在启动空压机前不停地搅拌，防止固体沉淀；按板、框的钮数为1－2－3－2－1－2－3－2－1的顺序排列号板框过滤机。

将滤布复在2号板框两侧，使其表面平整，然后用压紧螺杆压紧板和框；启动空气压缩机，第一次控制压力在;将计量筒放置在滤液出口出，记录液面的初始读数，准备好秒表；关闭洗水阀，打开滤液出口阀，开启滤浆进口旋塞，当有滤液连续流出时开始记录时间，计量筒中液面每上升3cm记录一次时间。

记录时两人用秒表同时间隔记录；当流出的滤液呈细线状流出时，则过滤已完毕，停止计时，关闭进口旋塞；关闭进水阀，滤液出口阀，开洗水进口阀进行洗涤。

洗水从滤液出口处流出时开始计时，每上升3cm记录一次时间，记录两组数据即可。

沉降与过滤一章习题及答案一、选择题1、一密度为7800 kg/m 3的小钢球在相对密度为1.2的某液体中的自由沉降速度为在20℃水中沉降速度的1/4000，则此溶液的粘度为（设沉降区为层流20℃水密度998.2 kg/m 3粘度为100.5×10-5Pa ·s ）。

A⋅A 4000mPa ·s ；⋅B 40mPa ·s ；⋅C 33.82Pa ·s ；⋅D 3382mPa ·s2、含尘气体在降尘室内按斯托克斯定律进行沉降。

理论上能完全除去30μm 的粒子，现气体处理量增大1倍，则该降尘室理论上能完全除去的最小粒径为。

DA ．m μ302⨯；B 。

m μ32/1⨯；C 。

m μ30；D 。

m μ302⨯ 3、降尘室的生产能力取决于。

BA ．沉降面积和降尘室高度；B ．沉降面积和能100%除去的最小颗粒的沉降速度；C ．降尘室长度和能100%除去的最小颗粒的沉降速度；D ．降尘室的宽度和高度。

45A C 6A 7A.粒子分离效率之和8A C 910A.1112A ．面积大，处理量大；B ．面积小，处理量大；C ．压差小，处理量小；D ．压差大，面积小 13、以下说法是正确的。

BA.过滤速率与A(过滤面积)成正比;B.过滤速率与A 2成正比;C.过滤速率与滤液体积成正比;D.过滤速率与滤布阻力成反比14、恒压过滤，如介质阻力不计，过滤压差增大一倍时，同一过滤时刻所得滤液量。

CA. 增大至原来的2倍;B.增大至原来的4倍;C.增大至原来的倍;D.增大至原来的1.5倍 15、过滤推动力一般是指。

BA ．过滤介质两边的压差；B.过滤介质与滤饼构成的过滤层两边的压差;C.滤饼两面的压差;D.液体进出过滤机的压差16、恒压板框过滤机，当操作压差增大1倍时，则在同样的时间里所得滤液量将（忽略介质阻力）。

A A ．增大至原来的2倍；B ．增大至原来的2倍；Ｃ．增大至原来的4倍；D ．不变17、若沉降室高度降低，则沉降时间；生产能力。

F - j =£d 3（：'s6由牛顿第二定律，有n -?）gdu F-F b-F D 6d3（；'S-'）g _3「」duEs?s-Jg 18l ud 2's积分空廿u l18»」d 2（Ps-p ）g 」d 2‘s 18」n （f所以 式中等速阶m/s。

第二部分计算题示例与分析2-93试推导球形颗粒从静止开始沉降至恰作等速沉降这一阶段的沉降速度随时间变化的 关系式。

设固体小球的直径为 d ，密度为［，静止流体的密度为?，粘度为J，沉降区满足斯托克斯定律。

分析：首先对自由沉降过程作受力分析，然后根据牛顿第二定律列出此变速运动阶段加速 度的表达式，即有关速度和时间的微分关系式，最后积分即可求出。

2 2解: 阻力FD =严：噫护：皿 净重力为重力减浮力du（y ）g~~18— u?sd2「sd%s 卄 °sd%s -18」（；i - :JgPsu = u t （1 _ e d s ）u ――变速阶段的沉降速度， m/s ；2-94现有一颗粒密度为 2650kg /m 3,直径为45」m 的球形石英粒子在 20 C 的空气中作 自由沉降，试计算：（1） 粒子由静止状态至达到其加速段终端速度（即沉降速度）的 9900所需的时间？（2）在该段下降的距离为多少？解：（1）先判断沉降区是否层流 设作滞流沉降的最大粒径为 d c则 U t= •代入斯托克斯定律，得 —dcPd c P18」查得20 C 空气代入求出 本题 由题d c =1.224 3?= 1.205kg/m 3 J=1.81 10乃 Pa s 6=2650g/m 3d c =57.3」md =45」m ：：： d 「故沉降区属滞流2-53 知u =u t-J 8P0 1 1 - e d 化d 2(d18 J :单] u = u t 1 —e匕U t 由题意 u =0.99u t ，代入上式，得—畧二 ln 0.01 —4.61U tg-：1-0.01U td 2(—(45 10冷2 2650汕‘北伽怡18」 18 1.81 10*v - 4.61u t /g = 4.610.1616/9.81 =0.076s- 迤 F 1-严（2）设h 为沉降距离，则Udh di积分上式可得颗粒在时间内下降的距离(e18心S"I)]18 1.81 10色0.07645210 少 2650_1)]h 二U t [- 0v - 0.076s 、u t =0.1616m/s 代入 (45汉10 )2 汇 2650“ h=0.1616[0.0765 (e18勺.8仆10 =0.1616[0.076 0.0165(e 4.6-1)9.64mm2 — 95有一降尘室，长 6m ，宽3m ，共20层，每层100mm ,用以除去炉气中的矿尘，矿 尘密度 匚=3000kg/m 3，炉气密度0.5kg/m 3，粘度0.035m Pa s ，现要除去炉气中10 "m 以上的颗粒，试求：（1 ）为完成上述任务，可允许的最大气流速度为多少？ （2 ）每小时最多可送入炉气若干？（3）若取消隔板，为完成任务该降尘室的最大处理量为多少？解：（1）设沉降区为滞流，则 u td 2（6」）g18」因为 ut「P s 》P 贝U_ （10 10 上）2 3000 9.81= 4.67mm/s18 0.035 10-3du”10 10»4.67 10’ 0.5 .. 4 ,如沁十仏= ----- 3= 6.67 乂 10 --------- < 1 假设正确 卩 0.035x10^由降尘室的分离条件，有L 4.6汉10彳><6 ccc ,u = U t 0.28m/ sH（2） V =20Au tRe t0.1=20 6 3 4.67 10" 3600=6052.3 m 3 / hU t d 2（「-，）gU t已知所以maxI 18u t u丫（PsBg；篇常。

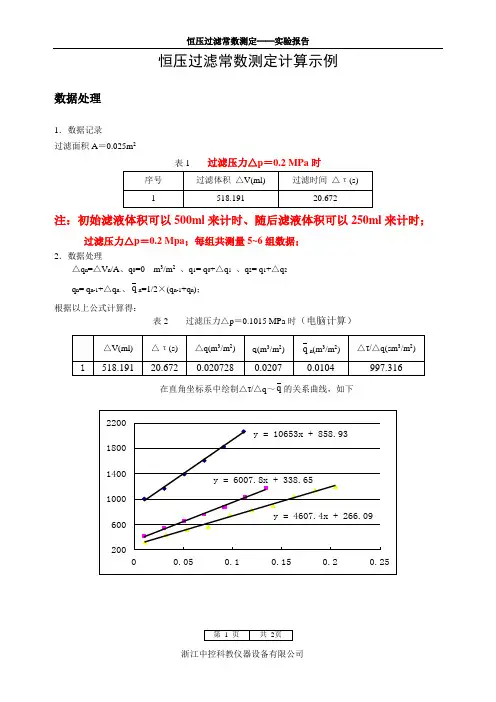
恒压过滤常数测定计算示例
数据处理
1．数据记录 过滤面积A ＝0.025m 2
表1 过滤压力△p ＝0.2 MPa 时
注：初始滤液体积可以500ml 来计时、随后滤液体积可以250ml 来计时；
过滤压力△p ＝0.2 Mpa ；每组共测量5~6组数据；
2．数据处理
△q n =△V n /A 、q 0=0 m 3/m 2 、q 1= q 0+△q 1 、q 2= q 1+△q 2
q n = q n-1+△q n 、、q n =1/2×(q n-1+q n )； 根据以上公式计算得：
表2 过滤压力△p ＝0.1015 MPa 时（电脑计算）
在直角坐标系中绘制△τ/△q ～q
的关系曲线，如下
第 2 页 共 2页
过滤常数S 以曲线斜率，以图中取点来算：
由 斜率：2S K =；截距： 2
e I q K
=；
则： 22,K m s S =、3
,2e KI I q m S
==、222,e e q I s K KS τ==；
表7（电脑计算） △p(Mp)
斜率S
截距I K
q e τe
lgK lg △p 0.1015
10653 858.93
0.000188 0.08063 34.627
-3.726 -0.9935
3.结果分析
过滤系数K 与过滤压力△p 成正比。

△p 变大时，K 也随着变大；△p 变小时，K 也随着变小
4.思考题1、2、3
三、实验装置与流程
本实验装置由空压机、配料槽、压力料槽、板框过滤机等组成，其流程示意如图1。

图1 板框压滤机过滤流程。

空气过滤器的计算方法
空气过滤器的计算方法主要包括以下步骤：
1.确定过滤器的过滤面积，根据实际需求和过滤器型号选
择合适的面积。

2.计算过滤器的过滤速度，即空气通过过滤器的速度，根
据实际需求和过滤器型号确定合适的速度。

3.根据过滤面积和过滤速度，计算过滤器的风量，即单位
时间内通过过滤器的空气体积。

4.根据实际需求，选择合适的过滤材料和过滤等级，以满
足空气净化的要求。

5.根据过滤器的使用环境和条件，选择合适的安装方式和
维护方法，以保证过滤器的正常运行和使用寿命。

通过以上步骤，可以合理地计算并选择适合的空气过滤器，实现对空气的有效净化，提高室内空气质量。

漆雾过滤器捕漆量计算公式在涂装行业中，漆雾过滤器是一种非常重要的设备，它能够有效地过滤掉喷漆过程中产生的漆雾，减少环境污染，保护工人的健康。

而漆雾过滤器的捕漆量是评价其性能的重要指标之一。

本文将介绍漆雾过滤器捕漆量的计算公式，并探讨影响捕漆量的因素。

漆雾过滤器捕漆量的计算公式如下：捕漆量 = (进入漆雾过滤器的漆雾质量出去漆雾过滤器的漆雾质量) / 进入漆雾过滤器的漆雾质量。

其中，进入漆雾过滤器的漆雾质量和出去漆雾过滤器的漆雾质量可以通过实验测量得到。

捕漆量的单位通常为百分比。

影响漆雾过滤器捕漆量的因素有很多，下面我们将重点介绍几个主要因素：1. 过滤器材料和结构。

漆雾过滤器的材料和结构对其捕漆量有着直接的影响。

一般来说，漆雾过滤器的材料越密集，结构越合理，捕漆量就越高。

常见的漆雾过滤器材料包括玻璃纤维、合成纤维和活性炭等。

不同材料的漆雾过滤器在捕漆量上会有所差异。

2. 气流速度。

气流速度是影响漆雾过滤器捕漆量的重要因素之一。

一般来说，气流速度越大，漆雾过滤器的捕漆量就越高。

但是，如果气流速度过大，可能会导致漆雾过滤器的堵塞，从而影响其性能。

因此，在实际应用中，需要根据具体情况确定合适的气流速度。

3. 漆雾粒径。

漆雾粒径是指漆雾颗粒的大小，它对漆雾过滤器的捕漆量也有着重要影响。

一般来说，漆雾粒径越小，漆雾过滤器的捕漆量就越高。

因此，在实际应用中，需要根据喷漆工艺确定合适的漆雾过滤器，以达到最佳的捕漆效果。

4. 操作条件。

除了以上几个因素外，操作条件也会对漆雾过滤器的捕漆量产生影响。

例如，温度、湿度、压力等因素都会影响漆雾过滤器的性能。

因此，在实际应用中，需要根据具体的操作条件对漆雾过滤器进行调整，以达到最佳的捕漆效果。

综上所述，漆雾过滤器捕漆量是评价其性能的重要指标之一，而影响捕漆量的因素有很多。

在实际应用中，需要根据具体情况选择合适的漆雾过滤器，并根据操作条件进行调整，以达到最佳的捕漆效果。

希望本文对大家了解漆雾过滤器的捕漆量有所帮助。

2024-2025学年湖南省长沙市长郡中学高一上学期期中考试数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知a∈R，若集合M={1,a}，N={−1,0,1}，则“a=0”是“M⊆N”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件2.下列命题是全称量词命题且为真命题的是A. ∀a，b∈R，a2+b2<0B. 菱形的两条对角线相等C. ∃x0∈R，x20=x0D. 一次函数的图象是直线3.设全集U=R，集合A={1,2,3,4,5}，B={x|3<x<8,x∈N}，则下图中的阴影部分表示的集合是A. {1,2,3,4,5}B. {3,4}C. {1,2,3}D. {4,5,6,7}4.若函数f(x)=4x2−kx−8在[5,8]上是单调函数，则实数k的取值范围是A. (−∞,40)B. (−∞,40]∪[64,+∞)C. [40,64]D. [64,+∞)5.已知关于x的不等式ax2+bx+c>0的解集为{x|13<x<12}，则不等式cx2+bx+a>0的解集为A. {x|−12<x<−13}B. {x|x>3或x<2}C. {x|2<x<3}D. {x|−3<x<−2}6.已知关于x的不等式2x+2x−a≥7在区间(a,+∞)上恒成立，则实数a的最小值为A. 1B. 32C. 2 D. 527.17世纪初，约翰·纳皮尔为了简化计算而发明了对数．对数的发明是数学史上的重大事件，恩格斯曾经把笛卡尔的坐标系、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为17世纪的三大数学发明．我们知道，任何一个正实数N可以表示成N=a×10n(1≤a<10,n∈Z)的形式，这便是科学记数法，若两边取常用对数，则有lg N=n+lg a.现给出部分常用对数值(如下表)，则可以估计22023的最高位的数值为真数x2345678910lg x(近0.301030.477120.602060.698970.778150.845100.903090.95424 1.000似值)A. 6B. 7C. 8D. 98.已知函数g(x)是R上的奇函数，且当x<0时，g(x)=−x2+2x，函数f(x)={x,x≤0,g(x),x>0,若f(2−x2 )>f(x)，则实数x的取值范围是A. (−2,1)B. (−∞,−2)∪(1,+∞)C. (1,2)D. (−∞,1)∪(2,+∞)二、多选题：本题共3小题，共18分。

过滤的实验报告处理引言过滤是一种常见的数据处理方法，在各个领域都有广泛的应用。

本实验旨在研究不同过滤方法对数据处理的效果，并进行比较和分析。

本实验采用了两种常见的过滤方法，即移动平均和中值滤波，通过实验数据的处理，评估它们在去除噪声和平滑数据等方面的效果。

实验目的1. 研究移动平均和中值滤波两种过滤方法的原理和实现方法；2. 利用实验数据，分别运用这两种方法进行数据处理；3. 比较和分析两种方法在去除噪声和平滑数据方面的效果，并结合实验数据得出结论。

实验方法移动平均过滤移动平均过滤是一种将当前数据和前面若干个数据的平均值作为当前数据的方法。

实验中我们选择了带权平均的移动平均过滤方法，即对前面的数据乘以不同的权重再求平均。

具体过程如下：1. 定义一个窗口的大小，一般为奇数，表示采样的数据个数；2. 将窗口滑动到数据流的起始位置；3. 取窗口中的数据，分别与对应的权重相乘；4. 将乘积相加，除以权重之和，得到平均值，即为过滤后的数据；5. 将窗口滑动到下一个位置，继续进行相同的操作，直至处理完所有数据。

中值滤波中值滤波是一种选择窗口中排序后的中间值作为当前数据的方法。

它主要用于去除离群值等异常数据。

具体过程如下：1. 定义一个窗口的大小，一般为奇数，表示采样的数据个数；2. 将窗口滑动到数据流的起始位置；3. 取窗口中的数据进行排序；4. 选择排序后的中间值作为过滤后的数据；5. 将窗口滑动到下一个位置，继续进行相同的操作，直至处理完所有数据。

实验数据我们选择了一个包含了噪声和平滑数据的实验数据，用于对移动平均和中值滤波进行处理。

原始数据如下：时间数据0 101 132 113 94 155 206 237 188 179 16实验结果与分析移动平均过滤我们选取窗口大小为3进行移动平均过滤处理，对实验数据进行平滑。

处理后的数据如下：时间数据0 101 11.332 113 114 11.675 16.336 19.337 20.338 19.339 17.67可以看出，移动平均过滤方法能够较好地平滑数据，减小了数据间的突变。

校核强制滤速计算引言：强制滤速是指通过外力或机械设备对悬浮颗粒进行滤速计算的过程。

在工程设计和设备运行过程中，正确计算和校核强制滤速是非常重要的。

本文将介绍强制滤速的计算方法，并给出一个校核强制滤速的例子。

一、强制滤速的计算方法：强制滤速的计算方法可以基于不同的模型，其中最常用的是达西定律和布斯玛定律。

1.达西定律：达西定律是一种经验公式，可以用于计算液体在过滤介质中的滤速。

达西定律可以表示如下：v=(K*ΔP)/η其中，v表示滤速，K表示达西系数，ΔP表示压力差，η表示液体的动力黏度。

达西系数K可以通过实验或经验确定。

对于不同过滤介质和悬浮物质，达西系数的取值范围可能有所不同。

2.布斯玛定律：布斯玛定律是一种能更准确描述颗粒在过滤介质中的沉降速度的公式。

布斯玛定律可以表示如下：v=(d^2*g*(ρp-ρf))/(18*η)其中，v表示滤速，d表示颗粒直径，g表示重力加速度，ρp表示颗粒的密度，ρf表示液体的密度，η表示液体的动力黏度。

布斯玛定律考虑了颗粒大小、重力加速度和液体及颗粒的密度等因素，所以相比达西定律，其计算结果更为准确。

二、校核强制滤速的例子：现假设有一个过滤器，过滤介质是圆形孔径为0.1mm的滤网，用于过滤直径为10μm的悬浮颗粒。

液体的液压头为5m，动力黏度为0.01 Pa·s。

1.计算达西定律的滤速：根据达西定律，需要先确定达西系数K的取值。

根据滤网的物理性质和实验数据，设K=0.01m/s·Pa。

2.计算布斯玛定律的滤速：根据布斯玛定律，直接代入公式计算滤速。

v = (d^2 * g * (ρp - ρf)) / (18 * η) = (10^-10 m^2 * 9.8m/s^2 * (1000 kg/m^3 - 1000 kg/m^3)) / (18 * 0.01 Pa·s) = 0 m/s 由于布斯玛定律考虑了颗粒直径的因素，如果颗粒直径非常小，布斯玛定律得出的滤速往往接近或等于零。

鱼缸过滤效能计算公式鱼缸过滤器是鱼缸中非常重要的一个设备，它可以帮助保持水质清洁，为鱼儿提供一个良好的生存环境。

而鱼缸过滤效能的计算是非常重要的，可以帮助我们了解过滤器的性能和适用范围。

下面我们来介绍一下鱼缸过滤效能的计算公式。

首先，我们需要了解一下鱼缸过滤效能的定义。

鱼缸过滤效能是指过滤器每小时可以处理的水量，通常以加仑/小时（GPH）或升/小时（LPH）来表示。

通过计算过滤效能，我们可以确定适合的过滤器大小和适用范围，以确保鱼缸中的水质得到有效的维护。

鱼缸过滤效能的计算公式如下：过滤效能 = 鱼缸容积×水循环次数。

其中，鱼缸容积指的是鱼缸的容积大小，通常以加仑（G）或升（L）来表示。

水循环次数指的是过滤器每小时可以处理的水量，通常以加仑/小时（GPH）或升/小时（LPH）来表示。

举个例子，假设我们有一个容积为20加仑的鱼缸，我们想要计算适合的过滤器大小和适用范围。

如果我们希望过滤器每小时可以处理鱼缸容积的3倍水量，那么我们可以使用以下公式来计算过滤效能：过滤效能 = 20加仑× 3 = 60加仑/小时。

通过这个计算，我们可以确定适合的过滤器大小为每小时处理60加仑的水量。

当然，实际情况中我们还需要考虑过滤器的品牌、型号、过滤方式等因素，以确保选择到合适的过滤器。

在实际使用过程中，我们还需要考虑一些其他因素，例如鱼缸中的鱼的种类和数量、饲料的投放量、水质的监测等。

这些因素都会影响鱼缸的水质和过滤效能的需求，因此在选择过滤器时需要综合考虑这些因素。

另外，鱼缸过滤效能的计算公式也可以根据实际情况进行调整。

如果鱼缸中的鱼的种类和数量较多，或者饲料的投放量较大，那么我们可以适当增加过滤效能的计算值，以确保鱼缸中的水质得到有效的维护。

总之，鱼缸过滤效能的计算是非常重要的，可以帮助我们选择适合的过滤器大小和适用范围，以确保鱼缸中的水质得到有效的维护。

通过以上介绍的计算公式和方法，希望可以帮助大家更好地了解和选择鱼缸过滤器，为鱼儿提供一个良好的生存环境。

化工过滤常数计算公式
化工过滤常数计算公式是一个用于描述过滤过程的重要公式。

过滤常数K，θe和qe是反映过滤介质阻力大小的常数，均称为介质常数，其单位分别为m2/s，s及m3/m2。

在恒压过滤时，过滤常数的计算公式可以表示为：
\[ \frac{\tau}{q}=\frac{1}{K}q+\frac{2}{K}q_e \]
在这个公式中，τ代表过滤时间，q代表单位过滤面积的滤液体积，K则是过滤常数。

此外，还有一种过滤基本方程：
\[ V = V + LA ⎫φ⎫⇒ L φεφ = φ = LA(1 −ε ) \]
其中，V是悬浮液总体积，L是滤饼厚度，φ是悬浮液含固量质量分数，(kg固体/kg悬浮液)，ε是悬浮液含固量体积分数，(m3固体/m3悬浮液) 。

过滤过程中很多因素都会影响到过滤常数，比如滤饼性质、滤浆性质、推动力（如压力）以及过滤介质的性质等。