空间直角坐标系及点的坐标表示
- 格式:ppt
- 大小:228.02 KB
- 文档页数:11

空间直角坐标系点坐标表示以空间直角坐标系点坐标表示为标题,本文将介绍空间直角坐标系的相关知识。
空间直角坐标系是一种常用的坐标系统,用于描述三维空间中的点的位置。
在空间直角坐标系中,每个点都可以用三个坐标值来表示,分别为x、y和z。
这三个坐标值分别代表了点在x轴、y轴和z轴上的位置。
其中,x轴是水平方向,y轴是垂直于x轴且在水平平面内的方向,z轴是垂直于水平平面的垂直方向。
这样,通过这三个坐标值的组合,我们可以准确地确定一个点在空间直角坐标系中的位置。
在空间直角坐标系中,每个坐标轴都有正方向和负方向。
正方向是从原点向右、向上和向外延伸的方向,负方向则是相反的方向。
通过正负号的不同,可以确定一个点在各个坐标轴上的位置。
举个例子,假设有一个点A,它在x轴上的坐标为2,y轴上的坐标为-3,z轴上的坐标为1。
那么在空间直角坐标系中,点A的位置可以表示为(2, -3, 1)。
这意味着点A位于x轴的正方向上2个单位处,位于y轴的负方向上3个单位处,位于z轴的正方向上1个单位处。
在空间直角坐标系中,我们可以通过计算两个点之间的距离来衡量它们之间的空间距离。
根据勾股定理,两个点之间的距离可以通过它们在各个坐标轴上的坐标差值计算得出。
例如,点A(2, -3, 1)和点B(-1, 4, 2)之间的距离可以计算为:AB = √[(x2 - x1)² + (y2 - y1)² + (z2 - z1)²]= √[(-1 - 2)² + (4 - (-3))² + (2 - 1)²]= √[9 + 49 + 1]= √59所以点A和点B之间的距离为√59个单位。
除了表示点的位置和计算距离外,空间直角坐标系还可以用于表示向量。
向量是具有大小和方向的量,可以用箭头表示。
在空间直角坐标系中,一个向量可以用起点和终点的坐标表示。
例如,向量AB 可以表示为(2, -3, 1)到(-1, 4, 2)的箭头。




空间直角坐标系的定义和坐标一、空间直角坐标系的定义和坐标1.空间直角坐标系在单位正方体$oabc-d′a′b′c′$中,以$o$点为原点,分别以射线$oa$,$oc$,$od′$的方向为正方向,以线段$oa$,$oc$,$od′$的长为单位长,建立三条数轴:$x$轴、$y$轴、$z$轴。
这时我们说建立了一个空间直角坐标系$oxyz$,其中点$o$叫做坐标原点,$x$轴、$y$轴、$z$轴叫做坐标轴。
通过每两个坐标轴的平面叫做坐标平面,分别称为$xoy$平面、$yoz$平面、$xoz$平面。
2.空间矢量的坐标一个向量在空间直角坐标系中的坐标等于表示向量的有向线段的终点坐标减去起点坐标。
如$a(x_1,y_1,z_1)$,$b(x_2,y_2,z_2)$,则$\overrightarrow{ab}=$$\overrightarrow{ob}-$$\overrightarrow{oa}=$$(x_2-x_1$,$y_2-y_1$,$z_2-z_1)$。
3.空间向量的坐标运算设$\boldsymbola(x_1,y_1,z_1)$,$\boldsymbolb(x_2,y_2,z_2)$,则(1) $\boldsymbola+\boldsymbolb=(x_1+x_2,y_1+y_2,z_1+z_2)$(2)$\boldsymbola-\boldsymbolb=(x_1-x_2,y_1-y_2,z_1-z_2)$。
(3) $\boldsymbola·\boldsymbolb=x_1x_2+y_1y_2+z_1z_2$(4)$|\boldsymbola|=\sqrt{x^2_1+y^2_1+z^2_1}$。
(5)$λ\boldsymbola=(λx_1,λy_1,λz_1)$4、空间向量平行(共线)与垂直的充要条件让非零向量$\boldsymbol(x_1,y_1,z_1)$,$\boldsymbol B(x_2,y_2,z_2)$,然后$\boldsymbola∥\boldsymbolb\leftrightarrow\frac{x_1}{x_2}=\frac{y_1}{y_2}=\frac{z_1}{z_2}=λ(λ∈\mathbf{r})$。


空间直角坐标系中点坐标公式在空间直角坐标系中,我们可以用三个数值来表示一个点的位置。
这三个数值分别代表了点在x轴、y轴和z轴的坐标。
我们可以将这三个坐标值写成一个有序三元组 (x, y, z)。
假设我们有一个点P,它在x轴上的坐标为x,y轴上的坐标为y,z 轴上的坐标为z。
那么点P的坐标可以表示为 (x, y, z)。
在三维空间中,点的坐标公式可以通过测量从原点到点P的三条边的长度得到。
根据勾股定理,我们可以得出以下关系:1. 点P在x轴上的坐标可以通过测量点P到y轴和z轴的距离得到。
这个距离可以表示为√(y^2 + z^2)。
所以点P在x轴上的坐标为x = √(y^2 + z^2)。
2. 点P在y轴上的坐标可以通过测量点P到x轴和z轴的距离得到。
这个距离可以表示为√(x^2 + z^2)。
所以点P在y轴上的坐标为y = √(x^2 + z^2)。
3. 点P在z轴上的坐标可以通过测量点P到x轴和y轴的距离得到。
这个距离可以表示为√(x^2 + y^2)。
所以点P在z轴上的坐标为z = √(x^2 + y^2)。
通过这个坐标公式,我们可以计算出点P在三维空间中的坐标。
例如,如果点P在x轴上的坐标为3,在y轴上的坐标为4,在z轴上的坐标为5,那么点P的坐标可以表示为 (3, 4, 5)。
通过这个坐标公式,我们可以方便地计算出点在空间中的位置。
同时,我们也可以通过这个公式来确定点在空间中的距离和方向。
总结起来,空间直角坐标系中点的坐标可以用有序三元组 (x, y, z) 表示,其中x代表点在x轴上的坐标,y代表点在y轴上的坐标,z 代表点在z轴上的坐标。
我们可以通过测量点到每个轴的距离得到点的坐标。
这个坐标公式在三维空间中有着广泛的应用,可以用来计算点的位置、距离和方向等信息。

本篇学习了空间直角坐标系、大地坐标系、平面坐标系、高斯平面直角坐标系。
这个个坐标系有时很容易弄混淆!(一)空间直角坐标系空间直角坐标系的坐标原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上切按右手系于X轴呈90度夹角,某点中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用如下图所示:(二)大地坐标系大地坐标系是采用大地纬度、经度和大地高程来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高程是空间的点沿着参考椭球的法线方向到参考椭球面的距离。
地面点的高程和国家高程基准(1)绝对高程。
地面点沿垂线方向至大地水准面的距离称为绝对高程或称海拔。
过去我国采用青岛验潮站(tide gauge station)1950~1956年观测成果求得的黄海平均海水面作为高程的零点,称为“1956年黄海高程系”(Huanghai height system1956水准原点高程为72.289m)。
后经复查,发现该高程系的验潮资料时间过短,准确性较差,改用青岛验潮站1950~1979年的观测资料重新推算,并命名为“1985年国家高程基准”(Chinese height datum 1985)。
国家水准原点(leveling origin高程为72.260m)设于青岛市观象山附近,作为我国高程测量的依据。
它的高程值是以“1985年国家高程基准”所确定的平均海水面为零点测算而得。
在使用原“1956年黄海高程系”的高程成果时,应注意将其换算为新的高程基准系统。
(2)相对高程。
地面点沿铅垂线方向至任意假定的水准面的距离称为该点的相对高程,亦称假定高程。
在图l—5中,地面点A和B的相对高程分别为H'A和H'B。
(3)高差。
地面上任意两点的高程(绝对高程或相对高程)之差称为高差。


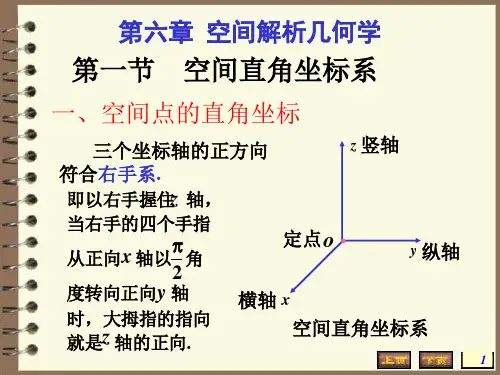
空间直角坐标系与空间直角坐标的表示在数学中,空间直角坐标系是一种用于描述三维空间中点位置的坐标系统。
它基于三个相互垂直的坐标轴,通常用x、y和z来表示,这三条坐标轴将空间划分为三个相互垂直的平面。
本文将介绍空间直角坐标系以及如何使用坐标系表示三维空间中的点。
一、空间直角坐标系的定义与特点空间直角坐标系是由三个相互垂直的坐标轴构成的。
通常情况下,我们将这三个坐标轴分别命名为x轴、y轴和z轴。
这三个坐标轴在空间中相交于一个点,这个点被称为坐标原点(0,0,0)。
x轴与y轴的交点定义为平面上的原点(0,0),x轴正方向与y轴正方向的夹角定义为正方向,即逆时针方向。
空间直角坐标系的特点如下:1. 三个坐标轴互相垂直,且共面,形成一个立方体。
2. 原点坐标为(0,0,0),表示三个坐标轴的交点。
3. 经过原点的平面称为底面,垂直于z轴的平面称为水平面。
这两个平面与坐标轴固定相对。
二、空间直角坐标的表示方法在空间直角坐标系中,每个点都可以表示为一个有序的三元组(x,y,z)。
根据点在坐标系中的位置,可以确定这个三元组的值。
以空间中的点P为例,假设它的坐标为(x,y,z)。
x表示点P到yoz平面的有向距离,当点P在x轴的负方向时,x值为负;y表示点P到xoz平面的有向距离,当点P在y轴的负方向时,y值为负;z表示点P 到xoy平面的有向距离,当点P在z轴的负方向时,z值为负。
在表示一个点的坐标过程中,我们需要关注一些特殊情况:1. 点在坐标轴上:当点P在x轴上时,其坐标为(0,y,z);当点P在y 轴上时,其坐标为(x,0,z);当点P在z轴上时,其坐标为(x,y,0)。
2. 坐标值为负数:当点P位于坐标轴的负方向时,对应坐标值为负数。
3. 特殊位置:坐标原点处的点坐标为(0,0,0),表示坐标轴交点。
使用空间直角坐标系的表示方法,我们可以清楚地描述三维空间中的点的位置关系。
这对于几何图形的表示、运动的研究以及计算机图形学等领域都具有重要的意义。
空间直角坐标系知识点空间直角坐标系是我们在学习数学、物理等科学领域常常遇到的一个重要概念。
它是一种表示三维空间中点位置的方法,通过三个相互垂直的坐标轴来确定点的位置。
本文将介绍空间直角坐标系的基本概念、坐标轴的方向以及一些常见的知识点。
一、空间直角坐标系的基本概念空间直角坐标系是由三个互相垂直的坐标轴构成的。
我们可以将这三个坐标轴分别标记为X轴、Y轴和Z轴。
在空间直角坐标系中,任意一个点的位置可以通过它在每一个坐标轴上的投影来确定。
在空间直角坐标系中,我们通常用(x,y,z)来表示一个点的坐标,其中x代表该点在X轴上的位置,y代表该点在Y轴上的位置,z代表该点在Z轴上的位置。
这三个坐标分别是实数。
二、坐标轴的方向在空间直角坐标系中,坐标轴的方向是固定的。
X轴的正方向为从左向右,Y轴的正方向为从下向上,Z轴的正方向为从后向前。
这个规定是为了统一表示、计算和解析几何的方向。
需要注意的是,不同的学科、领域可能对坐标轴的方向有所不同。
在一些物理学或工程学的问题中,X轴的正方向可能定义为从右向左,Y轴的正方向可能定义为从上向下,Z轴的正方向可能定义为从前向后。
因此,在应用空间直角坐标系时,我们需要根据具体问题确定坐标轴的方向。
三、常见的空间直角坐标系知识点1. 距离公式:在空间直角坐标系中,两点之间的距离可以通过勾股定理计算。
设两点分别为A(x1,y1,z1)和B(x2,y2,z2),则AB的距离为√((x2-x1)²+(y2-y1)²+(z2-z1)²)。
2. 坐标轴的平面:由X轴和Y轴组成的平面叫做XY平面,由X轴和Z轴组成的平面叫做XZ平面,由Y轴和Z轴组成的平面叫做YZ平面。
3. 坐标轴上的投影:在空间直角坐标系中,一个点在某个坐标轴上的投影就是它在该坐标轴上的坐标。
例如,一个点的投影坐标为(x,y,0),表示该点在XY平面上。
4. 坐标轴的正向和负向:在一个坐标轴上,正向是指从原点指向无穷大的方向,负向是指从原点指向负无穷大的方向。
空间坐标系空间坐标系是用来描述物体在空间中位置的一种数学工具。
在二维平面中,我们使用笛卡尔坐标系来表示物体的位置。
而在三维空间中,我们需要使用更加复杂的坐标系来准确描述物体的位置。
本文将介绍常见的空间坐标系,包括直角坐标系、极坐标系和球坐标系。
1. 直角坐标系直角坐标系是最常见的坐标系,也是最容易理解和使用的坐标系之一。
它由三个互相垂直的轴构成,分别称为x、y和z轴。
这三个轴的交点称为原点,它是空间中所有点的起点。
任意一点可以由它在x、y和z轴上的坐标表示,用(x, y, z)表示。
2. 极坐标系极坐标系是一种极其简洁的坐标系,它使用极径和极角来表示物体的位置。
极径表示物体到原点的距离,极角表示物体和x轴的夹角。
在极坐标系中,我们使用(r, θ)来表示一个点的位置。
其中,r为非负实数,表示距离,θ为角度,表示方向。
3. 球坐标系球坐标系是一种在三维空间中描述物体位置的坐标系。
它的原点位于球心,与直角坐标系不同的是,球坐标系中的轴并不垂直。
球坐标系由三个坐标参数组成,分别是极径r、极角θ和方位角φ。
极径r表示物体到球心的距离,极角θ表示物体到正z轴的夹角,方位角φ则表示投影到xy平面的夹角。
这三种坐标系在不同的应用场景下具有不同的优势。
直角坐标系适合描述物体在一个平面内的位置,对于三维空间中的物体来说,它提供了最直观的表示方法。
极坐标系适合描述物体在一个相对固定点周围的运动,比如天体运动中的行星轨迹。
球坐标系则适合描述物体在一个球体上的位置,比如地理信息系统中的三维地理位置。
总的来说,空间坐标系是用中文表示物体在三维空间中位置的一种数学工具。
它通过合适的坐标系,可以准确地描述物体在空间中的位置和运动。
不同的坐标系适用于不同的应用场景,我们可以根据具体情况选择合适的坐标系来进行描述和计算。
通过熟练掌握和运用空间坐标系,我们可以更好地理解和分析三维空间中的各种现象和问题。