NOIP2015提高组复赛试题Day2
- 格式:docx
- 大小:28.31 KB
- 文档页数:6

noip2015普及组复赛试题题目一:矩阵运算给定一个n阶方阵A(1 ≤ n ≤ 100),求A的所有指定行指定列删除后得到的新矩阵的行列式。
输入格式:输入第一行包含一个整数n,表示方阵的阶数。
接下来n行,每行包含n个整数,表示方阵A的元素。
接下来一行包含两个整数,表示要删除的行和列的序号。
输出格式:输出一个整数,表示新矩阵的行列式的值。
题目要求:首先,我们需要编写一个能够计算矩阵行列式的函数,然后根据题意进行修改,使其能够处理删除指定行列后的新矩阵,并返回新矩阵的行列式的值。
算法思路:我们可以使用拉普拉斯展开定理来计算矩阵行列式的值。
首先定义一个变量result,初始化为0。
然后遍历矩阵的第一行元素,对于第i 个元素,根据其正负性,计算其余元素组成的(n-1)阶子矩阵的行列式的值,并递归调用自身。
最后将每个元素计算得到的行列式值乘以其对应的元素,累加到result上。
然后根据题目要求,在计算每个元素对应的子矩阵时,判断是否需要删除指定的行列。
如果需要删除,则直接跳过该行列,否则继续计算。
代码如下:```pythondef determinant(matrix):n = len(matrix)if n == 1:return matrix[0][0]result = 0for i in range(n):if n > 2:sub_matrix = [row[:i] + row[i+1:] for row in matrix[1:]]else:sub_matrix = matrix[1:]det = determinant(sub_matrix)result += (-1) ** i * matrix[0][i] * detreturn resultn = int(input())matrix = []for _ in range(n):row = list(map(int, input().split()))matrix.append(row)row, col = map(int, input().split())matrix = [matrix[i][:col] + matrix[i][col+1:] for i in range(row)] # 删除指定列matrix = matrix[:row] + matrix[row+1:] # 删除指定行result = determinant(matrix)print(result)```题目二:水果分配小明和他的朋友们买了n个水果,其中有x个苹果和y个香蕉。


NOIP2015提高组day1第二题解题报告NOIP2015提高组复赛Day1第二题解题报告By 某蒟蒻zrw1.题目大概描述(因为写的时候题目还没放出来)几个小盆友们在传递自己的信息(生日),并且每个小盆友只会把自己知道的信息传给唯一的一个人【但是自己可以收到很多信息,并会在收到信息的下一轮把这些信息传给那个唯一的人】(单相思233333),问多少轮后自己会收到自己一开始传递出去的自己的信息。
输入:第一行一个整数n,表示有n个人接下来n行,每行一个数j,设这是除第一行外的第i行,那么j 表示第i个人只会把信息传给第j个人。
输出:一个整数,表示最少几轮后自己的信息会回到自己手中。
样例输入:52 4 23 1样例输出:3数据规模:100% n<=200000 60% n<=2500 30% 记不住了……2.大概需要什么样的算法根据数据规模,我们可以大概判断需要多少效率的算法,甚至有的时候可以猜出这题用的是什么算法。
对于本题来说,60%大概就是O(n^2)的算法了,一般是裸的暴力回溯或者是暴力广搜,也有用floyd的(我是从NOIP吧上看到的)。
如果要AC的话,算法效率至少要在O(nlogn)以下(log在这里是以2为底不是以10为底)。
然而,本题是有O(n)算法的,下面会讲。
3.我们还是画个图吧(图可能比较难看,但能看就行)画画图,就会知道这是在做一件什么事情了。
以样例数据为例:我们很容易发现,2,3,4,形成了一个环,而1和5,并没有什么卵用……所以在环234中,由于每一轮可以把在上一轮知道的信息传给唯一的下一个人,在234环中,就需要3轮,信息才能传到多画几个图(由于本人很懒,就只画一张特殊情况比较多的小图):(有木有一种贵圈真乱的感觉)我们可以看出来,1,5,6,成了一个环,而2,3,4,8,也成了一个环,7,9,是来打酱油的。
那么对于这两个环来说,因为每一轮可以传递上一轮信息给下一个人,所以显然是1,5,6这个环比较早传完,3轮。

noip2015提高组复赛试题答案一.单项选择题(共20题,每题1.5分,共计30分;每题有且仅有一个正确答案。
)1. 1MB等于()。
A. 1000字节B. 1024字节C. 1000⨯1000字节D. 1024⨯1024字节2. 在PC机中,PENTIUM(奔腾)、酷睿、赛扬等是指()。
A. 生产厂家名称B. 硬盘型号C. CPU的型号D. 显示器的型号3. 操作系统的作用是()。
A. 把源程序译成目标程序B. 便于进行数据管理C. 控制和管理系统资源D. 实现硬件之间的连接4. 在计算机内部用于传送、存贮、加工处理的数据或指令都是以()形式进行的。
A. 二进制码B. 八进制码C. 十进制码D. 智能拼音码5. 下列说法正确的是()。
A. CPU的主要任务是执行数据运算和程序控制B. 存储器具有记忆能力,其中信息任何时候都不会丢失C. 两个显示器屏幕尺寸相同,则它们的分辨率必定相同D. 个人用户只能使用Wifi的方式连接到Internet6.二进制数00100100和00010100的和是()。
A.00101000B. 01110011C.01000100D. 001110007. 与二进制小数0.1相等的十六进制数是()。
A. 0.8B. 0.4C. 0.2D. 0.18. 所谓中断是指()。
A. 操作系统随意停止一个程序的运行B. 当出现需要时,CPU暂时停止当前程序的执行转而执行处理新情况的过程C.因停机而停止一个程序的运行D.电脑死机9. 计算机病毒是()。
A. 通过计算机传播的危害人体健康的一种病毒B. 人为制造的能够侵入计算机系统并给计算机带来故障的程序或指令集合C.一种由于计算机元器件老化而产生的对生态环境有害的物质D.利用计算机的海量高速运算能力而研制出来的用于疾病预防的新型病毒10. FTP可以用于()。
A. 远程传输文件B. 发送电子邮件C. 浏览网页D. 网上聊天11.下面哪种软件不属于即时通信软件()。

Day1铺地毯【问题描述】为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。
一共有n 张地毯,编号从1 到n。
现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。
地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。
注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
【输入】输入文件名为 carpet.in。
输入共 n+2 行。
第一行,一个整数 n,表示总共有n 张地毯。
接下来的 n 行中,第i+1 行表示编号i 的地毯的信息,包含四个正整数a,b,g,k,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标(a,b)以及地毯在x轴和y 轴方向的长度。
第 n+2 行包含两个正整数x 和y,表示所求的地面的点的坐标(x,y)。
【输出】输出文件名为 carpet.out。
输出共 1 行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出-1。
【输入输出样例 1】【输入输出样例说明】如下图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,覆盖点(2,2)的最上面一张地毯是3 号地毯。
【输入输出样例 2】【输入输出样例说明】如上图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,点(4,5)没有被地毯覆盖,所以输出-1。
【数据范围】对于 30%的数据,有n≤2;对于 50%的数据,0≤a, b, g, k≤100;对于 100%的数据,有0≤n≤10,000,0≤a, b, g, k≤100,000。
【一句话题意】给定n个按顺序覆盖的矩形,求某个点最上方的矩形编号。
【考察知识点】枚举【思路】好吧我承认看到图片的一瞬间想到过二维树状数组和二维线段树。
置答案ans=-1,按顺序枚举所有矩形,如果点在矩形内则更新ans。
注意题中给出的不是对角坐标,实际上是(a,b)与(a+g,b+k)。
第二十一届全国青少年信息学奥林匹克联赛初赛提高组Pascal语言试题竞赛时间:2015年10月11日14:30~16:30选手注意:试题纸共有9页,答题纸共有2页,满分100分。
请在答题纸上作答,写在试题纸上的一律无效。
不得使用任何电子设备(如计算器、手机、电子词典等)或查阅任何书籍资料。
一、单项选择题(共15题,每题1.5分,共计22.5分;每题有且仅有一个正确选项)1. 在计算机内部用来传送、存贮、加工处理的数据或指令都是以()形式进行的。
A. 二进制码B. 八进制码C. 十进制码D. 智能拼音码2. 下列说法正确的是()。
A. CPU的主要任务是执行数据运算和程序控制B. 存储器具有记忆能力,其中信息任何时候都不会丢失C. 两个显示器屏幕尺寸相同,则它们的分辨率必定相同D. 个人用户只能使用Wifi的方式连接到Internet3. 与二进制小数0.1相等的十六进制数是()。
A. 0.8B. 0.4C. 0.2D. 0.14. 下面有四个数据组,每个组各有三个数据,其中第一个数据为八进制数,第二个数据为十进制数,第三个数据为十六进制数。
这四个数据组中三个数据相同的是()。
A. 120 82 50B. 144 100 68C. 300 200 C8D. 1762 1010 3F25. 线性表若采用链表存储结构,要求内存中可用存储单元地址()。
A. 必须连续B. 部分地址必须连续C. 一定不连续D. 连续不连续均可6. 今有一空栈S,对下列待进栈的数据元素序列a,b,c,d,e,f依次进行进栈,进栈,出栈,进栈,进栈,出栈的操作,则此操作完成后,栈S的栈顶元素为()。
A. fB. cC. aD. b7. 前序遍历序列与后序遍历序列相同的二叉树为()。
A. 非叶子结点只有左子树的二叉树B. 只有根结点的二叉树C. 根结点无右子树的二叉树D. 非叶子结点只有右子树的二叉树8. 如果根的高度为1,具有61个结点的完全二叉树的高度为()。
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)【问题描述】注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币(coin.cpp/c/pas)国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N 天每天收到N 枚金币后,骑士会在之后的连续N+1 天里,每天收到N+1 枚金币。
请计算在前K 天里,骑士一共获得了多少金币。
【输入格式】输入文件名为coin.in。
输入文件只有1 行,包含一个正整数K,表示发放金币的天数。
【输出格式】输出文件名为coin.out。
【问题描述】输出文件只有1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例1】【输入输出样例1 说明】骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。
因此一共收到1+2+2+3+3+3=14 枚金币。
【输入输出样例2】【数据说明】对于100%的数据,1 ≤ K ≤ 10,000。
2.扫雷游戏(mine.cpp/c/pas)扫雷游戏是一款十分经典的单机小游戏。
在n 行m 列的雷区中有一些格子含有地雷【问题描述】(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)【问题描述】注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币(coin.cpp/c/pas)国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N 天每天收到N 枚金币后,骑士会在之后的连续N+1 天里,每天收到N+1 枚金币。
请计算在前K 天里,骑士一共获得了多少金币。
【输入格式】输入文件名为coin.in。
输入文件只有1 行,包含一个正整数K,表示发放金币的天数。
【输出格式】输出文件名为coin.out。
输出文件只有1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例1】【问题描述】【输入输出样例1 说明】骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。
因此一共收到1+2+2+3+3+3=14 枚金币。
【输入输出样例2】【数据说明】对于100%的数据,1 ≤ K ≤ 10,000。
2.扫雷游戏(mine.cpp/c/pas)扫雷游戏是一款十分经典的单机小游戏。
在n 行m 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
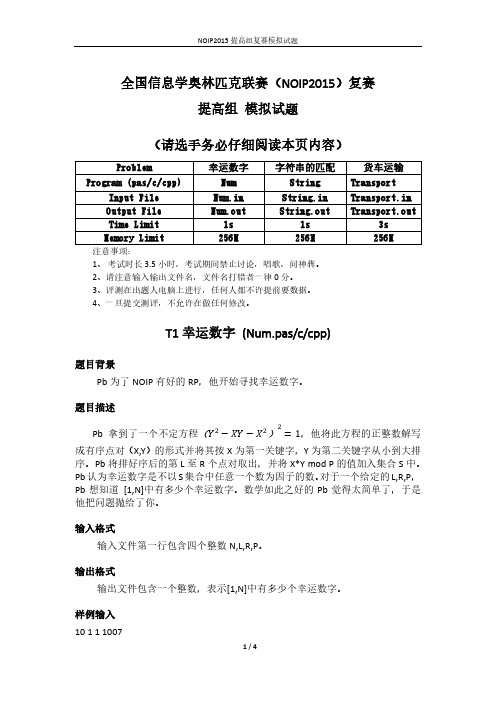
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛
提高组day2
(请选手务必仔细阅读本页内容)
一.题目概况
二.提交源程序文件名
三.编译命令(不包含任何优化开关)
注意事项:
1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数 main()的返回值类型必须是 int,程序正常结束时的返回值必须是 0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,
内存 4G,上述时限以此配置为准。
4、只提供 Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的 NOI Linux 下进行,各语言的编译器版本以其为准。
1.跳石头
(stone.cpp/c/pas)
【问题描述】
一年一度的“跳石头”比赛又要开始了!
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。
组委会已经选择好了两块岩石作为比赛起点和终点。
在起点和终点之间,有 N 块岩石(不含起点和终点的岩石)。
在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。
由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能移走起点和终点的岩石)。
【输入格式】
输入文件名为 stone.in。
输入文件第一行包含三个整数 L,N,M,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。
接下来 N 行,每行一个整数,第 i 行的整数 Di(0 < Di < L)表示第 i 块岩石与起点的距离。
这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
【输出格式】
输出文件名为 stone.out。
输出文件只包含一个整数,即最短跳跃距离的最大值。
【输入输出样例 1 说明】
将与起点距离为 2 和 14 的两个岩石移走后,最短的跳跃距离为 4(从与起点距离 17 的岩石跳到距离 21 的岩石,或者从距离 21 的岩石跳到终点)。
【输入输出样例 2】
见选手目录下的 stone/stone2.in 和 stone/stone2.ans。
【数据规模与约定】
对于 20%的数据,0 ≤ M ≤ N ≤ 10。
对于 50%的数据,0 ≤ M ≤ N ≤ 100。
对于 100%的数据,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。
2.子串
(substring.cpp/c/pas)
【问题描述】
有两个仅包含小写英文字母的字符串A和B。
现在要从字符串A中取出k个互不重叠的非空子串,然后把这k个子串按照其在字符串A中出现的顺序依次连接起来得到一个新的字符串,请问有多少种方案可以使得这个新串与字符串B 相等?注意:子串取出的位置不同也认为是不同的方案。
【输入格式】
输入文件名为 substring.in。
第一行是三个正整数 n,m,k,分别表示字符串 A 的长度,字符串 B 的长度,以及问题描述中所提到的 k,每两个整数之间用一个空格隔开。
第二行包含一个长度为 n 的字符串,表示字符串A。
第三行包含一个长度为 m 的字符串,表示字符串B。
【输出格式】
输出文件名为 substring.out。
输出共一行,包含一个整数,表示所求方案数。
由于答案可能很大,所以这里要求输出答案对 1,000,000,007 取模的结果。
【输入输出样例 1】
【输入输出样例 2】
【输入输出样例 3】
【输入输出样例说明】
所有合法方案如下:(加下划线的部分表示取出的子串)
样例 1:aab aab / aab aab
样例 2:a ab aab / a aba ab / a a ba ab / aab a ab
aa b aab / aa baa b / aab aa b
样例 3:a a b aab / a a baa b / a ab a a b / a aba a b
a a
b a a b / a a ba a b / aab a a b
【输入输出样例 4】
见选手目录下 substring/substring4.in 与 substring/substring4.ans。
【数据规模与约定】
对于第 1 组数据:1≤n≤500,1≤m≤50,k=1;
对于第 2 组至第 3 组数据:1≤n≤500,1≤m≤50,k=2;
对于第 4 组至第 5 组数据:1≤n≤500,1≤m≤50,k=m;
对于第 1 组至第 7 组数据:1≤n≤500,1≤m≤50,1≤k≤m;
对于第 1 组至第 9 组数据:1≤n≤1000,1≤m≤100,1≤k≤m;
对于所有 10 组数据:1≤n≤1000,1≤m≤200,1≤k≤m。
3. 运输计划
(transport.cpp/c/pas)
【问题描述】
公元 2044 年,人类进入了宇宙纪元。
L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。
小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。
显然,飞船驶过一条航道是需要时间的,对于航道j,任意飞船驶过它所花费的时间为tj,并且任意两艘飞船之间不会产生任何干扰。
为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。
在虫洞建设完成后,这 m 个运输计划会同时开始,所有飞船一起出发。
当这 m 个运输计划都完成时,小 P 的物流公司的阶段性工作就完成了。
如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少?
【输入格式】
输入文件名为 transport.in。
第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。
接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和ti,表示第 i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。
接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j 个运输计划是从 uj 号星球飞往 vj 号星球。
【输出格式】
输出文件名为 transport.out。
共 1 行,包含 1 个整数,表示小 P 的物流公司完成阶段性工作所需要的最短时间。
【输入输出样例 1 说明】
将第 1 条航道改造成虫洞:则三个计划耗时分别为:11、12、11,故需要花费的时间为 12。
将第 2 条航道改造成虫洞:则三个计划耗时分别为:7、15、11,故需要花
费的时间为 15。
将第 3 条航道改造成虫洞:则三个计划耗时分别为:4、8、11,故需要花费的时间为 11。
将第 4 条航道改造成虫洞:则三个计划耗时分别为:11、15、5,故需要花
费的时间为 15。
将第 5 条航道改造成虫洞:则三个计划耗时分别为:11、10、6,故需要花
费的时间为 11。
故将第 3 条或第 5 条航道改造成虫洞均可使得完成阶段性工作的耗时最短,需要花费的时间为 11。
【样例输入输出 2】
见选手目录下的 transport/transport2.in 与 transport/transport2.ans。
【数据规模与约定】。