云南省大理州南涧彝族自治县2016-2017学年高一数学下学期6月月考试题

2016-2017学年云南省大理州南涧县民族中学高一（上）12月月考数学试卷一、选择题（本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合A={1，2，3}，B={y|y=2x﹣1，x∈A}，则A∩B=（）A．{1，3}B．{1，2}C．{2，3}D．{1，2，3}2．函数f（x）=+的定义域为（）A．（﹣3，0 C．（﹣∞，﹣3）∪（﹣3，03．若sinα=﹣，则α为第四象限角，则tanα的值等于（）A．B．﹣C．D．﹣4．sin（﹣945°）的值为（）A．﹣B．C．﹣D．.5．若sinαtanα＜0，且＜0，则角α是（）A．第一象限B．第二象限C．第三象限D．第四象限6．设a=log37，b=21.1，c=0.83.1，则（）A．b＜a＜c B．c＜a＜b C．c＜b＜a D．a＜c＜b7．设函数f（x）=，若f（f（））=4，则b=（）A．1 B．C．D．8．若方程lnx+x﹣5=0在区间（a，b）（a，b∈Z，且b﹣a=1）上有一实根，则a的值为（）A．5 B．4 C．3 D．29．已知A为锐角，lg（1+cosA）=m，lg=n，则lgsinA的值为（）A．m+B．m﹣n C．（m+）D．（m﹣n）10．已知函数f（x）是定义在R上的奇函数，且当x≥0时，f（x）=x2﹣2x，则y=f（x）在R上的解析式为（）A．f（x）=﹣x（x+2）B．f（x）=|x|（x﹣2）C．f（x）=x（|x|﹣2）D．f （x）=|x|（|x|﹣2）11．函数f（x）=1+log2x与g（x）=21﹣x在同一直角坐标系下的图象大致是（）A．B． C．D．12．已知函数f（x）=2sin（ωx+φ）对任意x都有，则等于（）A．2或0 B．﹣2或2 C．0 D．﹣2或0二、填空题（本大题共4个小题，每个小题5分，共20分）13．已知4a=2，lgx=a，则x=．14．幂函数f（x）的图象过点（3，），则f（x）的解析式是．15．已知，且θ是第二象限角，则tanθ=．16．定义在R上的奇函数f（x），当x∈（0，+∞）时，f（x）=log2x，则不等式f（x）＜﹣1的解集是．三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．（10分）已知（1）求函数f（x）的最大值及取得最大值时自变量x的集合；（2）求函数f（x）的单调减区间．18．（12分）计算：（1）（2）．19．（12分）已知（x∈R），若f（x）满足f（﹣x）+f（x）=0，（1）求实数a的值及f（3）；（2）判断函数的单调性，并加以证明．20．（12分）求值；（1）sin（﹣1 200°）cos 1 290°+cos（﹣1 020°）•sin（﹣1 050°）（2）设，求．21．（12分）已知在△ABC中sinA+cosA=，（1）求sinA•cosA．（2）判断△ABC是锐角还是钝角三角形．（3）求tanA值．22．（12分）已知a∈R，函数f（x）=log2（+a）．（1）当a=1时，解不等式f（x）＞1；（2）若关于x的方程f（x）+log2（x2）=0的解集中恰有一个元素，求a的值；（3）设a＞0，若对任意t∈，1t，t+1，1t，t+1，1，1t，t+1，1，1hslx3y3h 上单调递减，∴t=时，g（t）取得最大值，=．∴．∴a的取值范围是．【点评】本题考查了对数函数的运算法则单调性、不等式的解法、利用导数研究函数的单调性极值与最值，考查了分类讨论方法、推理能力与计算能力，属于难题．。

南涧县民族中学2016——2017学年上学期9月月考高一数学试题班级 姓名 学号本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

注:所有题目在答题卡上做答第I 卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是最符合题目要求的。

）1.设集合M={0，1，2}，N={x ∈N|x ﹣1≥0}，则M ∩N=（ ） A ．{1} B ．{2} C ．{0，1} D ．{1，2}2.下列关系正确的是（ ）A ．0∈NB ．1⊆RC ．{π}⊆QD ．﹣3∉Z3.设集合A={1，2，3}，B={4，5}，C={x|x=b ﹣a ，a ∈A ，b ∈B}，则C 中元素的个数是（ ） A ．3B ．4C ．5D ．64.集合{1,2,3}的所有真子集的个数为( )A ．3B ．6C ．7D ．85.已知集合A ＝{x|a －1≤x ≤a ＋2}，B ＝{x|3＜x ＜5}，则使A ⊇B 成立的实数a 的取 值范围是 ( ) A.{a|3＜a ≤4}B.{a|3≤a ≤4}C.{a|3＜a ＜4}D.φ6.已知集合A ＝{1,3}，B ＝{1，m }，A ∪B ＝A ，则m ＝ ( )． A ．0或 3 B ．0或3 C ．1或 3 D ．1或37. 已知x x f 23)(-=，x x x g 2)(2-=，⎩⎨⎧<≥=),()(),(),()(),()(x g x f x f x g x f x g x F 若若则)(x F 的最值是( )A ．最大值为3，最小值为－1B ．最大值为3，无最小值C ．最大值为7－27，无最小值D ．既无最大值，又无最小值8. 二次函数f (x )＝ax 2＋2a 是区间[－a ，a 2]上的偶函数，又g (x )＝f (x －1)，则(0)g ，3()2g ，(3)g 的大小关系为( )A ．3()2g <(0)g <(3)gB ．(0)g <3()2g <(3)g C ．3()2g <(3)g <(0)g D ．(3)g <3()2g <(0)g9. 下列四组函数，表示同一函数的是 （ ）（A ）f (x )＝2x , g (x )＝x （B ） f (x )＝x , g (x )＝xx 2（C ）f (x )＝42-x , g (x )＝22-+x x （D ）f (x )＝|x ＋1|, g (x )＝⎩⎨⎧-<---≥+1111x x x x10.函数()y f x =的定义域为[1,5]，则函数)12(-=x f y 的定义域是（ ） A ．[1,5] B ．[2,10] C ．[1,3] D ．[1,9]11．函数222,03,f ()6,20,x x x x x x x ⎧-≤≤⎪=⎨+-≤<⎪⎩的值域是( )A ．RB ．[1，＋∞)C ．[－8，1]D ．[－9，1]12．若f (x )满足对任意的实数a ，b 都有f (a ＋b )＝f (a )·f (b )且f (1)＝2，则f （2）f （1）＋f （4）f （3）＋f （6）f （5）＋…＋f （2 016）f （2 015）＝( ) A ．1 007 B ．1 008 C ．2 015D ．2 016第Ⅱ卷（非选择题 共90分）二、填空题（本大题共4小题， 每小题5分，共20分，把答案填在题中横线上）。

南涧县2016——2017学年下学期3月月考高一数学试题班级 姓名 学号本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

注:所有题目在答题卡上做答第I 卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是最符合题目要求的。

）1.已知集合A ＝{－2，0，2}，B ＝{x|x 2－x －2＝0}，则A∩B＝( )A ．∅B ．{2}C ．{0}D ．{－2}2．若 1.12log 3, 2.1,lg2lg5,a b c ===+则,,a b c 的大小关系为( )A. b a c >>B. a b c >>C. c b a >>D.无法确定3.一个长方体的棱长分别为1、2、2，它的顶点都在同一个球面上，这个球的体积为（ ）A ．B ．C ．D ． 4.已知sin α＝35，则cos(π－2α)＝ （ ） A ．－45 B ．－725 C ．725 D ．455.已知向量(,1)a t =和(2,2)b t =-+，若a b ⊥，则||a b += （ ）A ．64B ．8C ．5D 6.为了得到函数3cos 2y x =的图象，只需把函数3sin(2)6y x π=+的图象上所有的点（ ）A ．向右平移3π个单位 B ．向右平移6π个单位 C ．向左平移3π个单位 D ．向左平移6π个单位 7.设f(x)是周期为2的奇函数，当0≤x ≤1时，f(x)＝2x(1－x)，则f(－52)等于 （ ） A ．－12 B ．－14 C.14 D.128.设m ,n 是两条不同的直线，α,β是两个不同的平面.下列命题正确的是（ ）A ．若,,m n m n αβ⊂⊂⊥，则αβ⊥B ．若,,//m n αβαβ⊥⊥，则//m nC ．若//,,//m n αβαβ⊥，则 m n ⊥D ．若,,m n m αβαβ⊥=⊥，则n β⊥9.如图1，函数)2sin()(φ+=x A x f 2||,0(πφ<>A )的图象过点)3,0(，则)(x f 的图象的一个对称中心是（ ）A ．(,0)3π-B ．(,0)4πC ．(,0)6πD ．(,0)6π- 10、如图，网格纸上小正方形的边长为1，粗线画出的为某几何体的三视图，则此几何体的体积为（ ）A ．B ．1C ．D ．211.将函数sin ()y x x x R =+∈的图象向右平移θ（θ＞0）个单位长度后，所得到的图象关于y 轴对称，则θ的最小值是 （ ）A ．12πB ．6πC ．3πD ．56π 12.如图，正方体ABCD ﹣A 1B 1C 1D 1中，E 、F 分别是AB 、BC 的中点，过点D 1、E 、F 的截面将正方体分割成两个部分，记这两个部分的体积分别为V 1、V 2（V 1＜V 2），则V 1：V 2=（ ）。

云南高一高中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.设全集，则=( )A ．B ．C ．D ．2.下列各组函数是同一函数的是( ) A ．B ．C ．D ．3.下列函数中，在R 上是增函数的是( ) A ．B ．C ．D ．4.已知集合，设，则集合的真子集个数为( )A ．8B ．7C ．6D ．55.已知，则＝( )A ．－3B ．1C ．－1D ．46.函数的单调增区间依次为( )A ．(－∞，0] ，[1，＋∞)B ．(－∞，0]，(－∞，1]C ．[0，＋∞)， [1，＋∞)D ．[0，＋∞)，(－∞，1]7.下列说法中正确的有( )①若任取x 1，x 2∈I ，当x 1＜x 2时，f (x 1)＜f (x 2)，则y ＝f (x)在I 上是增函数； ②函数y ＝x 2在R 上是增函数； ③函数y ＝－在定义域上是增函数；④y ＝的单调递减区间是(－∞，0)∪(0，＋∞)．A ．0个B ．1个C ．2个D ．3个8.函数f (x)＝－x 2＋4x ＋a ，x ∈[0,1]，若f (x)有最小值－2，则f (x)的最大值为( ) A ．－1 B ．0 C ．1D ．29.已知函数f (x)在区间[a ，b]上单调，且，则函数的图象与x 轴在区间[a ，b] 内( )A ．至多有一个交点B ．必有唯一个交点C．至少有一个交点D．没有交点10.若方程内有解，则的图象可能是( )11.设是非空集合，定义，已知，，则等于( )A．B．C．D．12.是定义在上的减函数，则的取值范围是( )A．[B．[]C．(D．(]13.(本题满分10分) 集合,求实数的值.二、填空题1.已知全集=,或,,则 .2.已知集合A=，用列举法表示集合A= .3.已知，则的定义域为 .4.若函数在区间上单调递减，则实数的取值范围是 .三、解答题1.（本题满分12分）已知二次函数的最小值为－1，且，（Ⅰ）求的值；（Ⅱ）求在上的单调区间与值域.2.（本题满分12分）已知函数，（Ⅰ）求的定义域和值域；（Ⅱ）判断函数在区间（2，5）上的单调性，并用定义来证明所得结论.3.（本题满分12分）已知函数（Ⅰ）若在是减函数，在是增函数，求实数的值；（Ⅱ）求实数的取值范围，使在区间上是单调函数，并指出相应的单调性.4.(本题满分12分）我国是水资源匮乏的国家，为鼓励节约用水，某市打算出台一项水费政策措施.规定：每季度每人用水量不超过5吨时，每吨水费收基本价1.3元；若超过5吨而不超过6吨时，超过部分的水费按基本价3倍收取；若超过6吨而不超过7吨时，超过部分的水费按基本价5倍收取.某人本季度实际用水量为吨，应交水费为元。

高考资源网（ ），您身边的高考专家投稿兼职请联系：2355394692 云南省大理州南涧县2016-2017学年高一数学下学期期中试题 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

注:所有题目在答题卡上做答Ⅰ卷一、选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．已知集合S={1，2}，设S 的真子集有m 个，则m=（ ）A ．4B ．3C ．2D ．12.函数122)(-+=x x x f 的定义域为（ ） A .[)+∞-,2 B .()+∞-,2 C .()()+∞-,00,2 D .[)()+∞-,00,23．一个球的体积等于其表面积，那么这个球的半径为（ ）A ．3B ．2C ．1D ．12 4．已知(,0)2x π∈-，4cos 5x =，则=x 2tan （ ） A ．247 B ．247- C ．724- D ．724 5．直线l 过圆22(3)4x y +-=的圆心，且与直线10x y ++=垂直，则l 的方程为（ ）A ．20x y +-=B ．20x y -+=C ．30x y +-=D ．30x y -+=6.2,2==，且()⊥-，则与的夹角是（ ） A . 6π B . 4π C . 3π D . 125π 7.使得函数221ln )(-+=x x x f 有零点的一个区间是（ ） A . ()1,0 B . ()2,1 C . ()3,2 D .()4,38．点P 在直线012=+-y x 上，O 为坐标原点，则OP 的最小值是（ ）A ．33B ．51 C ． 5 D ．55 9．若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是( )．A ．18 3cmB ．12 3cmC ．9 3cmD ．24 3cm10．在正四棱锥ABCD P -中，所有的棱长均为2，则侧棱与底面投稿兼职请联系：2355394692 2ABCD 所成的角和该四棱锥的体积分别为（ ）A .︒45B .︒30C . ︒60D .75︒11．设00sin14cos14a =+，00sin16cos16b =+，2c =，则,,a b c 大小关系是( ) A ．a b c << B ．b a c << C ．c b a <<D ．a c b << 12．已知a ，b ，c ，d 都是常数，a ＞b ，c ＞d ，若f （x ）=2017﹣（x ﹣a ）（x ﹣b ）的零点为c ，d ，则下列不等式正确的是（ ）A ．a ＞c ＞b ＞dB ．a ＞b ＞c ＞dC ．c ＞d ＞a ＞bD ．c ＞a ＞b ＞d二、填空题：（本大题共4小题，每小题5分，共20分.）的值等于 ．14.已知与均为单位向量，它们的夹角为︒60-等于 ．15.已知定点A (0，1)，点B 在直线0x y +=上运动，当线段AB 最短时，点B 的坐标 ．16．已知两条直线m ，n 和两个平面α，β，下面给出四个命题中：①m αβ=，n α⊂⇒m ∥n 或m 与n 相交；②α∥β，m α⊂，n β⊂⇒m ∥n ；③m ∥n ，m ∥α⇒n ∥α；④m αβ=，m ∥n ⇒n ∥β且n ∥α．其中正确命题的序号是 ．Ⅱ卷三、解答题：（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分10分）求经过两条直线2-330x y -=和20x y ++=的交点且与直线310x y +-=平行的直线l 的方程．18.（本小题满分12分）圆经过点(2,3),(25).A B ---，(1)若圆的面积最小，求圆的方程；（2）若圆心在直线230x y --=上，求圆的方程。

云南省大理州南涧彝族自治县2016-2017学年高一数学下学期6月月考试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

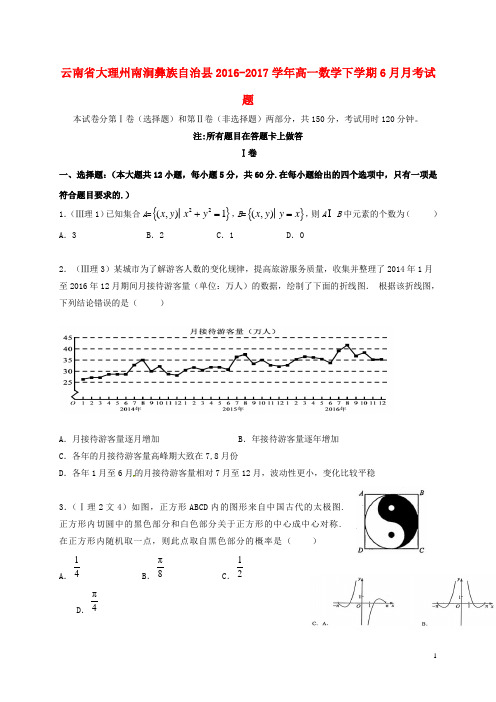
注:所有题目在答题卡上做答Ⅰ卷一、选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．（Ⅲ理1）已知集合A={}22(,)1x y x y+=│，B={}(,)x y y x=│，则A I B中元素的个数为（）A．3 B．2 C．1 D．02．（Ⅲ理3）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加 B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7,8月份D．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳3．（Ⅰ理2文4）如图，正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是（）A．14 B．π8 C．12D．π44.（Ⅱ文4）设非零向量a ，b 满足+=-b b a a 则（ ） A.a ⊥b B. =b a C. a ∥b D. >b a5.（Ⅱ理4文6）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）A ．90πB ．63πC ．42πD ．36π6．（Ⅰ文6）如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是（ ）7.（Ⅱ文11）从分别写有1,2,3,4,5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为（ ） A.110 B.15 C.310D.258．（Ⅲ理6）设函数f (x )=cos(x +3π)，则下列结论错误的是（ ） A ．f (x )的一个周期为−2π B ．y =f (x )的图像关于直线x =83π对称 C ．f (x +π)的一个零点为x =6π D ．f (x )在(2π,π)单调递减 9．（Ⅰ理8文10）右面程序框图是为了求出满足3n−2n>1000的最小偶数n ，那么在和两个空白框中，可以分别填入（ ）A ．A >1 000和n =n +1B ．A >1 000和n =n +2C ．A ≤1 000和n =n +1D ．A ≤1 000和n =n +210．（Ⅲ理8、文9）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（ ） A ．πB ．3π4C ．π2D ．π411．（Ⅰ理5）函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是（ ） A ．[2,2]-B ．[1,1]-C ．[0,4]D ．[1,3]12．（Ⅰ文8）.函数sin21cos xy x=-的部分图像大致为（ ）二、填空题：（本大题共4小题，每小题5分，共20分.）13.（Ⅰ理13）已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2 b |= . 14.（Ⅰ文15）已知π(0)2a ∈，,tan α=2，则πcos ()4α-=__________。

南涧县2016—2017学年下学期6月月考高一语文试题第Ⅰ卷阅读题现代文阅读（35分）论述类文本阅读阅读下面的文字，完成下列各题。

立足于儒家的新人文主义，仍然需要证明其自身的独特价值何在。

因为在人类思想史和文明史上，至少存在过两种人文主义：一是文艺复兴到启蒙时代的人文主义，二是20世纪前期美国学者白璧德的新人文主义。

基于儒家资源的新人文主义，与它们有何区别呢？从文艺复兴到启蒙时代的人文主义，是一种针对中世纪基督教黑暗时代的人文主义，它强调的是摆脱以上帝为中心的思维方式，而发现人性、人的尊严、人的价值，要求在生活世界和思维世界中，确立人的主体性地位，运用人的理性能力，使人自由地发展其本性。

这种人文主义最终走向了人类中心主义。

它和现代性有一种深层次的联系，即世俗或凡俗的兴起。

这种兴起曾在政治、经济、文化上产生了积极的作用。

但同时，这种人文主义忽略了对人的精神领域的关注，有巨大的空白与缺陷；另外，它因为对个体的过度强调，形成了一种原子主义的自我观念，进而扩展到民族、国家和文化观念，于是民族冲突、国家冲突和文化冲突成为一种必然；另外，当对人的理性的强调成为一种绝对的肯定后，工具理性在很大程度上便压缩了人自身的生活世界和心灵领域，造成了对人自身的伤害。

因此，这种人文主义在造就现代社会巨大成就的同时，也埋下了现代性弊病的根源。

为此，在20世纪初期，美国学者白璧德提出了一种新的人文主义。

白璧德认为旧人文主义认为人可以无限发展是有问题的，所以他的新人文主义要以平衡和自律来改善人的境况。

同时，白璧德也重视东方的智慧，这一倾向，直接影响了他的数位中国学生，如吴宓、梅光迪等，这在20世纪中国思想界中造就了《学衡》一派。

具体来讲，白璧德指出了西方思想犯了过度夸大理性作用和过分强调实用主义的错误，由此，人很难在情感与理性、统一与杂多之间获得平衡，而失去了这种平衡，就使得人类沦入了过度的自然主义或科学主义。

而白璧德的新人文主义则要重建一种人能平衡自身情感与理性的能力，即建设一种真正的克制，这种克制比知识或同情心要更为重要。

2016-2017学年云南省大理州南涧民族中学高二（下）6月月考数学试卷（文科）一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）已知集合A＝{x|lg（x﹣2）＜1}，集合B＝{x|＜2x＜8}，则A∩B等于（）A．（2，12）B．（2，3）C．（﹣1，3）D．（﹣1，12）2．（5分）复数z＝（其中i是虚数单位）的虚部为（）A．B．C．D．3．（5分）某市教育主管部门为了全面了解2017届高三学生的学习情况，决定对该市参加2017年高三第一次全国大联考统考（后称统考）的32所学校进行抽样调查；将参加统考的32所学校进行编号，依次为1到32，现用系统抽样法，抽取8所学校进行调查，若抽到的最大编号为31，则最小的编号是（）A．2B．1C．4D．34．（5分）已知点A（﹣1，1），B（1，2），C（2，3），且，则λ＝（）A．B．C．D．5．（5分）已知平面α与两条不重合的直线a，b，则“a⊥α，且b⊥α”是“a∥b”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件6．（5分）已知函数f（x）＝cos（x+）sin x，则函数f（x）的图象（）A．最小正周期为T＝2πB．关于点（，﹣）对称C．在区间（0，）上为减函数D．关于直线x＝对称7．（5分）某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）A．4B．2C．D．88．（5分）抛掷两枚质地均匀的正四面体骰子，其4个面分别标有数字1，2，3，4，记每次抛掷朝下一面的数字中较大者为a（若两数相等，则取该数），平均数为b，则事件“a﹣b＝1”发生的概率为（）A．B．C．D．9．（5分）函数y＝（x﹣）sin x的图象是（）A．B．C．D．10．（5分）设x，y满足约束条件，若目标函数z＝x+y的最小值为，则实数a的值为（）A．2B．﹣2C．3D．﹣311．（5分）已知双曲线＝1（a＞0，b＞0）的右焦点为F，过F作斜率为﹣1的直线交双曲线的渐近线于点P，点P在第一象限，O为坐标原点，若△OFP的面积为，则该双曲线的离心率为（）A．B．C．D．12．（5分）数列{a n}满足a1＝，且对任意n∈N*，a n+1＝a n2+a n，c n＝，数列{c n}的前n项和为S n，则S2017的整数部分是（）A．1B．2C．3D．4二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）执行如图所示的程序框图，当输出i的值是4时，输入的整数n的最大值是．14．（5分）抛物线C：y2＝4x的焦点为F，设过点F的直线l交抛物线与A，B两点，且，则|BF|＝．15．（5分）设函数f（x）＝，若f（x）在区间[m，4]上的值域为[﹣1，2]，则实数m的取值范围为．16．（5分）球O为正方体ABCD﹣A1B1C1D1的内切球，AB＝2，E，F分别为棱AD，CC1的中点，则直线EF被球O截得的线段长为．三、解答题（6个大题共70分，写出必要的解答过程）17．（12分）已知等差数列{a n}的前n项和为S n，a4＝9，S3＝15．（1）求S n；（2）设数列的前n项和为T n，证明：．18．（12分）全世界越来越关注环境保护问题，某监测站点于2016年8月某日起连续n天监测空气质量指数（AQI），数据统计如下：（1）根据所给统计表和频率分布直方图中的信息求出n，m的值，并完成頻率分布直方图：（2）由頻率分布直方图，求该组数据的平均数与中位数；（3）在空气质量指数分别为51﹣100和151﹣200的监测数据中，用分层抽样的方法抽取5天，从中任意选取2天，求事件A“两天空气都为良”发生的概率．19．（12分）如图，在三棱柱ABC﹣A1B1C1中，底面△ABC是等边三角形，且AA1⊥平面ABC，D为AB的中点．（Ⅰ）求证：直线BC1∥平面A1CD；（Ⅱ）若AB＝BB1＝2，E是BB1的中点，求三棱锥A1﹣CDE的体积．20．（12分）已知离心率为的椭圆过点，点F1，F2分别为椭圆的左、右焦点，过F1的直线l与C交于A，B两点，且．（1）求椭圆C的方程；（2）求证：以AB为直径的圆过坐标原点．21．（12分）已知函数y＝lnx﹣mx（m∈R）（1）若函数y＝f（x）过点P（1，﹣1），求曲线y＝f（x）在点P处的切线方程；（2）求函数f（x）在区间[1，e]上的最大值．请考生在第22-23题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）已知直线l的极坐标方程为ρ＝，曲线C的参数方程为，（φ为参数）（1）写出直线l的普通方程与曲线C的直角坐标方程；（2）设曲线C经过伸缩变换得到曲线C′，求直线l被曲线C′截得的弦长．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣3|（Ⅰ）若不等式f（x﹣1）+f（x）＜a的解集为空集，求a的范围；（Ⅱ）若|a|＜1，|b|＜3，且a≠0，求证：f（ab）＞|a|f（）．2016-2017学年云南省大理州南涧民族中学高二（下）6月月考数学试卷（文科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）已知集合A＝{x|lg（x﹣2）＜1}，集合B＝{x|＜2x＜8}，则A∩B等于（）A．（2，12）B．（2，3）C．（﹣1，3）D．（﹣1，12）【解答】解：由A中的不等式变形得：lg（x﹣2）＜1＝lg10，即0＜x﹣2＜10，解得：2＜x＜12，即A＝（2，12）；由B中的不等式变形得：2﹣1＝＜2x＜8＝23，即﹣1＜x＜3，∴B＝（﹣1，3），则A∩B＝（2，3）．故选：B．2．（5分）复数z＝（其中i是虚数单位）的虚部为（）A．B．C．D．【解答】解：∵z＝＝，∴复数z＝的虚部为．故选：C．3．（5分）某市教育主管部门为了全面了解2017届高三学生的学习情况，决定对该市参加2017年高三第一次全国大联考统考（后称统考）的32所学校进行抽样调查；将参加统考的32所学校进行编号，依次为1到32，现用系统抽样法，抽取8所学校进行调查，若抽到的最大编号为31，则最小的编号是（）A．2B．1C．4D．3【解答】解：根据系统抽样法，总体分成8组，组距为＝4，若抽到的最大编号为31，则最小的编号是3．故选：D．4．（5分）已知点A（﹣1，1），B（1，2），C（2，3），且，则λ＝（）A．B．C．D．【解答】解：＝（2，1），+λ＝（1+3λ，1+2λ）．∵，∴•（+λ）＝2（1+3λ）+1+2λ＝0，解得λ＝．故选：B．5．（5分）已知平面α与两条不重合的直线a，b，则“a⊥α，且b⊥α”是“a∥b”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：a⊥α，且b⊥α⇒a∥b，反之不成立．可能a，b分别于α，β斜交．∴“a⊥α，且b⊥α”是“a∥b”的充分不必要条件．故选：A．6．（5分）已知函数f（x）＝cos（x+）sin x，则函数f（x）的图象（）A．最小正周期为T＝2πB．关于点（，﹣）对称C．在区间（0，）上为减函数D．关于直线x＝对称【解答】解：∵函数f（x）＝cos（x+）sin x＝（cos x﹣sin x）•sin x＝sin2x﹣•＝（sin2x+cos2x）﹣＝sin（2x+）﹣，故它的最小正周期为＝π，故A不正确；令x＝，求得f（x）＝﹣＝，为函数f（x）的最大值，故函数f（x）的图象关于直线x＝对称，且f（x）的图象不关于点（，）对称，故B不正确、D正确；在区间（0，）上，2x+∈（，），f（x）＝sin（2x+）﹣为增函数，故C不正确，故选：D．7．（5分）某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）A．4B．2C．D．8【解答】解：三视图复原的几何体是长方体，长方体长、宽、高分别是：2，2，3，所以这个几何体的体积是2×2×3＝12，长方体被一个平面所截，得到的几何体的是长方体的，如图所示，则这个几何体的体积为12×＝8．故选：D．8．（5分）抛掷两枚质地均匀的正四面体骰子，其4个面分别标有数字1，2，3，4，记每次抛掷朝下一面的数字中较大者为a（若两数相等，则取该数），平均数为b，则事件“a﹣b＝1”发生的概率为（）A．B．C．D．【解答】解：抛掷两枚质地均匀的正四面体骰子，其4个面分别标有数字1，2，3，4，记每次抛掷朝下一面的数字中较大者为a（若两数相等，则取该数），平均数为b，基本事件总数n＝4×4＝16，事件“a﹣b＝1“包含的基本事件有：（1，3），（3，1），（2，4），（4，2），共有4个，∴事件“a﹣b＝1”发生的概率为p＝＝．故选：B．9．（5分）函数y＝（x﹣）sin x的图象是（）A．B．C．D．【解答】解：函数是偶函数，当x∈（0，1）时，y＜0，且x＝1是函数的零点，A、B、C均不符，只有D符合．故选：D．10．（5分）设x，y满足约束条件，若目标函数z＝x+y的最小值为，则实数a的值为（）A．2B．﹣2C．3D．﹣3【解答】解：作出不等式组对应的平面区域如图：（阴影部分ABC）．由z＝x+y得y＝﹣x+z，平移直线y＝﹣x+z，由图象可知当直线y＝﹣x+z经过点B时，直线y＝﹣x+z的截距最小，此时z最小．由，解得，即B（，﹣），同时B也在直线3x﹣y﹣a＝0上，即3×﹣（﹣）﹣a＝0．则a＝2．故选：A．11．（5分）已知双曲线＝1（a＞0，b＞0）的右焦点为F，过F作斜率为﹣1的直线交双曲线的渐近线于点P，点P在第一象限，O为坐标原点，若△OFP的面积为，则该双曲线的离心率为（）A．B．C．D．【解答】解：设右焦点F（c，0），则过F且斜率为﹣1的直线l方程为y＝c﹣x∵直线l交双曲线的渐近线于点P，且点P在第一象限∴为解得P（，）∵△OFP的面积为，∴•c•＝整理得a＝3b∴该双曲线的离心率为＝＝故选：C．12．（5分）数列{a n}满足a1＝，且对任意n∈N*，a n+1＝a n2+a n，c n＝，数列{c n}的前n项和为S n，则S2017的整数部分是（）A．1B．2C．3D．4【解答】解：∵a n+1＝+a n，a1＝，∴a n+1＞a n．∴a2＝+＝，a3＝+＝，a4＝+＝＞1．∴n≥4时，∈（0，1）．∵a n+1＝+a n，∴＝﹣，可得：＝﹣，∴c n＝﹣，∴数列{c n}的前n项和S n＝++…+＝﹣．∴S2017＝﹣＝3﹣∈（2，3）．其整数部分为2．故选：B．二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）执行如图所示的程序框图，当输出i的值是4时，输入的整数n的最大值是23．【解答】解：模拟程序的运行，可得S＝0，T＝1，i＝1S＝1≤n，T＝2，S＝3，i＝2S＝5≤n，T＝4，S＝9，i＝3S＝12≤n，T＝8，S＝n，i＝4S＝24＞n，输出i＝4，故输入的整数n的最大值是23．故答案为：23．14．（5分）抛物线C：y2＝4x的焦点为F，设过点F的直线l交抛物线与A，B两点，且，则|BF|＝4．【解答】解：易知F坐标（1，0）准线方程为x＝﹣1．设过F点直线方程为y＝k（x﹣1）代入抛物线方程，得k2（x﹣1）2＝4x．化简后为：k2x2﹣（2k2+4）x+k2＝0．设A（x1，y1），B（x2，y2）则有x1x2＝1根据抛物线性质可知，|AF|＝x1+1，|BF|＝x2+1∴+＝＝1，又由，可得，则|BF|＝4．．故答案为：415．（5分）设函数f（x）＝，若f（x）在区间[m，4]上的值域为[﹣1，2]，则实数m的取值范围为[﹣8，﹣1]．【解答】解：函数f（x）的图象如图所示，结合图象易得当m∈[﹣8，﹣1]时，f（x）∈[﹣1，2]．故答案为：[﹣8，﹣1]．16．（5分）球O为正方体ABCD﹣A1B1C1D1的内切球，AB＝2，E，F分别为棱AD，CC1的中点，则直线EF被球O截得的线段长为．【解答】解：连结OE，OF，取EF的中点M，连结OM．∵O是正方体的中心，E，F是AD，CC1的中点，∴OE＝OF＝，∴OM⊥EF．又EF＝＝，∴OM＝＝．∵球O的半径为r＝1，∴EF被球O截得弦长为2＝．故答案为：．三、解答题（6个大题共70分，写出必要的解答过程）17．（12分）已知等差数列{a n}的前n项和为S n，a4＝9，S3＝15．（1）求S n；（2）设数列的前n项和为T n，证明：．【解答】解：（1）设等差数列{a n}的公差为d，S3＝（a1+a3）×3＝3a2＝15⇒a2＝5，∴，a1＝3，∴a n＝3+2（n﹣1）＝2n+1，；（2）证明：＝（﹣），则＝（1+﹣﹣）＝﹣（+）＜．18．（12分）全世界越来越关注环境保护问题，某监测站点于2016年8月某日起连续n天监测空气质量指数（AQI），数据统计如下：（1）根据所给统计表和频率分布直方图中的信息求出n，m的值，并完成頻率分布直方图：（2）由頻率分布直方图，求该组数据的平均数与中位数；（3）在空气质量指数分别为51﹣100和151﹣200的监测数据中，用分层抽样的方法抽取5天，从中任意选取2天，求事件A“两天空气都为良”发生的概率．【解答】解：（1）∵，∴n＝100，∵20+40+m+10+5＝100，∴m＝25，．由此完成频率分布直方图，如下图：（2）由频率分布直方图得该组数据的平均数为：＝25×0.004×50+75×0.008×50+125×0.005×50+175×0.002×50+225×0.001×50＝95，∵[0，50）的频率为0.004×50＝0.2，[50，100）的频率为：0.008×50＝0.4，∴中位数为：50+＝87.5．（3）在空气质量指数为51﹣100和151﹣200的监测天数中分别抽取4天和1天，在所抽収的5天中，将空气质量指数为51﹣100的4天分别记为a，b，c，d；将空气质量指数为151﹣200的1天记为e，从中任取2天的基本事件分别为：（a，b），（a，c），（a，d），（a，e），（b，c），（b，d），（b，e），（c，d），（c，e），（d，e）共10种，其中事件A“两天空气都为良”包含的基本事件为：（a，b），（a，c），（a，d），（b，c），（b，d），（c，d）共6种，所以事件A“两天都为良”发生的概率是．19．（12分）如图，在三棱柱ABC﹣A1B1C1中，底面△ABC是等边三角形，且AA1⊥平面ABC，D为AB的中点．（Ⅰ）求证：直线BC1∥平面A1CD；（Ⅱ）若AB＝BB1＝2，E是BB1的中点，求三棱锥A1﹣CDE的体积．【解答】（Ⅰ）证明：连接AC1，交A1C于点F，则F为AC1的中点，又D为AB的中点，∴BC1∥DF，又BC1⊄平面A1CD，DF⊂平面A1CD，∴BC1∥平面A1CD；（Ⅱ）解：三棱锥A1﹣CDE的体积．其中三棱锥A1﹣CDE的高h等于点C到平面ABB1A1的距离，可知．又．∴．20．（12分）已知离心率为的椭圆过点，点F1，F2分别为椭圆的左、右焦点，过F1的直线l与C交于A，B两点，且．（1）求椭圆C的方程；（2）求证：以AB为直径的圆过坐标原点．【解答】解：（1）点F1，F2分别为椭圆的左右焦点，椭圆的方程为；由离心率为得：；过点得：；所以，，b＝1；椭圆方程为；（2）证明：由（1）知F1（﹣1，0），F2（1，0）；令A（x1，y1），B（x2，y2）；当直线l的斜率不存在时，直线方程为l：x＝﹣1；此时，，不满足；设直线方程为l：y＝k（x+1）；代入椭圆方程得：（1+2k2）x2+4k2x+2k2﹣2＝0△＝16k4﹣4×（1+2k2）（2k2﹣2）＞0韦达定理：，；所以，，y1y2＝k2（x1x2+x2+x1+1）＝﹣；所以，；点F2到直线l的距离为；所以，由得：k2＝2；∵，∴所以，以AB为直径的圆过坐标原点．21．（12分）已知函数y＝lnx﹣mx（m∈R）（1）若函数y＝f（x）过点P（1，﹣1），求曲线y＝f（x）在点P处的切线方程；（2）求函数f（x）在区间[1，e]上的最大值．【解答】21、解：（1）因为点P（1，﹣1）在曲线y＝f（x）上，所以﹣m＝﹣1，解得m＝1．因为f'（x）＝﹣1＝0，所以切线的斜率为0，所以切线方程为y＝﹣1．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）（2）因为f'（x）＝﹣m＝，①当m≤0时，在区间[1，e]上，f'（x）＞0，所以函数f（x）在[1，e]上单调递增，则最大值为f（e）＝1﹣me；②当≥e，即0＜m≤时，f'（x）＞0，所以函数f（x）在[1，e]上单调递增，则最大值为f（e）＝1﹣me；③当1＜＜e，即＜m＜1，函数f（x）在（1，）上单调递增，在（，e）上单调递减，则最大值f（）＝﹣lnm﹣1；④当0＜＜e，即m≥1时，f'（x）＜0，函数f（x）在（1，e）上单调递减，则最大值f（1）＝﹣m．．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）综上，当m≤时，最大值为1＝me；当＜m＜1时，则最大值﹣lnm﹣1；当m≥1时，最大值﹣m．．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）请考生在第22-23题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）已知直线l的极坐标方程为ρ＝，曲线C的参数方程为，（φ为参数）（1）写出直线l的普通方程与曲线C的直角坐标方程；（2）设曲线C经过伸缩变换得到曲线C′，求直线l被曲线C′截得的弦长．（1）直线l的极坐标方程为ρ＝，展开为：ρ【解答】解：＝，化为直角坐标方程：x+y﹣2＝0．曲线C的参数方程为，（φ为参数），利用平方关系消去参数φ可得普通方程：x2+y2＝4．（2）由伸缩变换得到，代入方程：x2+y2＝4．可得：（x′）2+4（y′）2＝4，可得方程：+y2＝1．直线l被曲线C′截得的弦长＝2＝2．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣3|（Ⅰ）若不等式f（x﹣1）+f（x）＜a的解集为空集，求a的范围；（Ⅱ）若|a|＜1，|b|＜3，且a≠0，求证：f（ab）＞|a|f（）．【解答】解：（Ⅰ）函数f（x）＝|x﹣3|，不等式f（x﹣1）+f（x）＜a，即|x﹣4|+|x﹣3|＜a．再根据f（x﹣1）+f（x）＜a的解集为空集，可得|x﹣4|+|x﹣3|＜a的解集为空集．而|x﹣4|+|x﹣3|≥|（x﹣4）﹣（x﹣3）|＝1，∴a≤1．（Ⅱ）∵|a|＜1，|b|＜3，且a≠0，∴f（ab）＞|a|f（），等价于|ab﹣3|＞|a|•|﹣3|，等价于|ab﹣3|﹣|b﹣3a|，等价于（ab﹣3）2＞（b﹣3a）2．再根据（ab﹣3）2﹣（b﹣3a）2＝a2b2﹣9a2﹣b2+9＝（a2﹣1）（b2﹣9）＞0，可得f（ab）＞|a|f（）成立．。

2016-2017学年云南省大理州南涧县民族中学高一（下）开学数学试卷一、选择题（共12小题，每小题5分，满分60分）1．（5分）已知全集U={0，1，2，3，4}，集合M={1，2，3}，N={0，3，4}，则（∁U M）∩N（）A．{0，4}B．{3，4}C．{1，2}D．∅2．（5分）下列四个函数中，在（0，+∞）上为增函数的是（）A．f（x）=3﹣x B．f（x）=x2﹣3x C．f（x）=﹣D．f（x）=﹣|x| 3．（5分）如果a＞0，b＜﹣1，那么函数f（x）=ax+b的图象经过（）A．第一、二、四象限B．第二、三、四象限C．第一、二、三象限D．第一、三、四象限4．（5分）若a、b是任意实数，且a＞b，则（）A．a2＞b2B．C．lg（a﹣b）＞0 D．5．（5分）函数f（x）=3x+x﹣2的零点所在的一个区间是（）A．（﹣2，﹣1）B．（﹣1，0）C．（0，1） D．（1，2）6．（5分）已知函数，若f（a）+f（2）=0，则实数a的值等于（）A．﹣7 B．﹣5 C．﹣1 D．﹣37．（5分）下列各组函数f（x）与g（x）的图象相同的是（）A．B．f（x）=x2，g（x）=（x+1）2C．f（x）=1，g（x）=x0D．8．（5分）过点P（﹣1，3），且垂直于直线x﹣2y+m=0的直线方程为（）A．2x+y﹣1=0 B．2x+y﹣5=0 C．x+2y﹣5=0 D．x﹣2y+7=09．（5分）如果直线ax+2y+2=0与直线3x﹣y﹣2=0平行，则a=（）A．﹣3 B．﹣ C．﹣6 D．10．（5分）圆的一条直径的两个端点是（2，0），（0，2）时，则此圆的方程是（）A．（x﹣2）2+（y﹣1）2=1 B．（x﹣1）2+（y﹣1）2=2 C．（x﹣1）2+（y+1）2=9 D．（x+2）2+（y+1）2=211．（5分）若直线3x+y+a=0过圆x2+y2+2x﹣4y=0的圆心，则a的值为（）A．﹣1 B．1 C．3 D．﹣312．（5分）若直线x﹣y=2被圆（x﹣a）2+y2=4所截得的弦长为，则实数a 的值为（）A．﹣1或B．1或3 C．﹣2或6 D．0或4二、填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）．13．（5分）若2a=5b=10，则=．14．（5分）已知函f（x）=，则f（f（））=．15．（5分）已知过点A（﹣2，m）和B（m，4）的直线与直线2x+y﹣1=0平行，则m的值为．16．（5分）圆x2+y2﹣4x+2y=0上一点P（1，1）的圆的切线方程为：．三．解答题：要求写出计算或证明步骤（本大题共6小题，共70分，写出证明过程或演算步骤）17．（10分）求值：（I）；（II）．18．（12分）设A={x2﹣8x+15=0}，B={x|ax﹣1=0}，若B⊆A，求实数a组成的集合，并写出它的所有非空真子集．19．（12分）已知函数f（x）=log a（a x﹣1）（a＞0，a≠1）．（1）求函数f（x）的定义域；（2）讨论函数f（x）的单调性．20．（12分）求经过两条直线l1：x+y﹣4=0和l2：x﹣y+2=0的交点，且分别与直线2x﹣y﹣1=0（1）平行的直线方程；（2）垂直的直线方程．21．（12分）m为何值时，方程x2+y2﹣4x+2my+2m2﹣2m+1=0表示圆，并求半径最大时圆的方程．22．（12分）某租赁公司拥有汽车100辆．当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．（Ⅰ）当每辆车的月租金定为3600元时，能租出多少辆车？（Ⅱ）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？2016-2017学年云南省大理州南涧县民族中学高一（下）开学数学试卷参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2017春•南涧县校级月考）已知全集U={0，1，2，3，4}，集合M={1，2，3}，N={0，3，4}，则（∁U M）∩N（）A．{0，4}B．{3，4}C．{1，2}D．∅【解答】解：∁U M={0，4}，∴（∁U M）∩N={0，4}．故选：A．2．（5分）（2013秋•榆树市校级期末）下列四个函数中，在（0，+∞）上为增函数的是（）A．f（x）=3﹣x B．f（x）=x2﹣3x C．f（x）=﹣D．f（x）=﹣|x|【解答】解：∵f（x）=3﹣x在（0，+∞）上为减函数，∴A不正确；∵f（x）=x2﹣3x是开口向上对称轴为x=的抛物线，所以它在（0，+∞）上先减后增，∴B不正确；∵f（x）=﹣在（0，+∞）上y随x的增大而增大，所它为增函数，∴C正确；∵f（x）=﹣|x|在（0，+∞）上y随x的增大而减小，所以它为减函数，∴D不正确．故选C．3．（5分）（2013秋•肇庆期末）如果a＞0，b＜﹣1，那么函数f（x）=ax+b的图象经过（）A．第一、二、四象限B．第二、三、四象限C．第一、二、三象限D．第一、三、四象限【解答】解：∵a＞0，∴直线f（x）=ax+b的斜率a＞0，∵b＜﹣1，∴f（0）=b＜﹣1，∴函数f（x）=ax+b的图象经过一，三，四象限．故选：D．4．（5分）（1993•全国）若a、b是任意实数，且a＞b，则（）A．a2＞b2B．C．lg（a﹣b）＞0 D．【解答】解：a、b是任意实数，且a＞b，如果a=0，b=﹣2，显然A不正确；如果a=0，b=﹣2，显然B无意义，不正确；如果a=0，b=﹣，显然C，lg＞0，不正确；满足指数函数的性质，正确．故选D．5．（5分）（2015•福建模拟）函数f（x）=3x+x﹣2的零点所在的一个区间是（）A．（﹣2，﹣1）B．（﹣1，0）C．（0，1） D．（1，2）【解答】解：∵函数f（x）=3x+x﹣2，f（0）=1﹣2=﹣1＜0，f（1）=2＞0，f（0）f（1）＜0．根据函数的零点的判定定理可得函数f（x）=3x+x﹣2的零点所在的一个区间是（0，1），故选C．6．（5分）（2014春•衡南县期末）已知函数，若f（a）+f（2）=0，则实数a的值等于（）A．﹣7 B．﹣5 C．﹣1 D．﹣3【解答】解：由分段函数可知f（2）=2×2=4，∴由f（a）+f（2）=0得f（a）=﹣f（2）=﹣4，若a＞0，由f（a）=﹣4，得2a=﹣4，解得a=﹣2，∴此时不成立．若a≤0，由f（a）=﹣4，得a+1=﹣4，解得a=﹣5，∴a=﹣5成立．综上：a=﹣5．故选：B．7．（5分）（2010秋•武汉期末）下列各组函数f（x）与g（x）的图象相同的是（）A．B．f（x）=x2，g（x）=（x+1）2C．f（x）=1，g（x）=x0D．【解答】解：f（x）=x与g（x）=的定义域不同，故不是同一函数，∴图象不相同．f（x）=x2与g（x）=（x+1）2的对应关系不同，故不是同一函数，∴图象不相同．f（x）=1与g（x）=x0的定义域不同，故不是同一函数，∴图象不相同．f（x）=|x|与g（x）=具有相同的定义域、值域、对应关系，故是同一函数，∴图象相同．故选D．8．（5分）（2017春•南涧县校级月考）过点P（﹣1，3），且垂直于直线x﹣2y+m=0的直线方程为（）A．2x+y﹣1=0 B．2x+y﹣5=0 C．x+2y﹣5=0 D．x﹣2y+7=0【解答】解：设所求的直线方程为2x+y+c=0，把点P（﹣1，3）的坐标代入得﹣2+3+c=0，∴c=﹣1，故所求的直线的方程为2x+y﹣1=0，故选A．9．（5分）（2015秋•怀柔区期末）如果直线ax+2y+2=0与直线3x﹣y﹣2=0平行，则a=（）A．﹣3 B．﹣ C．﹣6 D．【解答】解：由于直线ax+2y+2=0与直线3x﹣y﹣2=0平行，故它们的斜率相等，故有﹣=3，解得a=﹣6，故选C．10．（5分）（2017春•南涧县校级月考）圆的一条直径的两个端点是（2，0），（0，2）时，则此圆的方程是（）A．（x﹣2）2+（y﹣1）2=1 B．（x﹣1）2+（y﹣1）2=2 C．（x﹣1）2+（y+1）2=9 D．（x+2）2+（y+1）2=2【解答】解：圆的圆心为线段的中点（1，1），半径为，∴要求的圆的方程为（x﹣1）2+（y﹣1）2=2，故选：B．11．（5分）（2011•安徽）若直线3x+y+a=0过圆x2+y2+2x﹣4y=0的圆心，则a的值为（）A．﹣1 B．1 C．3 D．﹣3【解答】解：圆x2+y2+2x﹣4y=0的圆心为（﹣1，2），代入直线3x+y+a=0得：﹣3+2+a=0，∴a=1，故选B．12．（5分）（2016•河南校级二模）若直线x﹣y=2被圆（x﹣a）2+y2=4所截得的弦长为，则实数a的值为（）A．﹣1或B．1或3 C．﹣2或6 D．0或4【解答】解：∵圆（x﹣a）2+y2=4∴圆心为：（a，0），半径为：2圆心到直线的距离为：∵解得a=4，或a=0故选D．二、填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）．13．（5分）（2016秋•荆门期末）若2a=5b=10，则=1．【解答】解：因为2a=5b=10，故a=log210，b=log510=1故答案为1．14．（5分）（2016•湖南模拟）已知函f（x）=，则f（f（））=．【解答】解：由分段函数可知f（）=，f（f（））=f（﹣2）=．故答案为：．15．（5分）（2016秋•大武口区校级期末）已知过点A（﹣2，m）和B（m，4）的直线与直线2x+y﹣1=0平行，则m的值为﹣8．【解答】解：∵过点A（﹣2，m）、B（m，4）的直线与直线2x+y﹣1=0平行，∴=﹣2，解得m=﹣8．故答案为：﹣8．16．（5分）（2017春•南涧县校级月考）圆x2+y2﹣4x+2y=0上一点P（1，1）的圆的切线方程为：x﹣2y+1=0．【解答】解：x2+y2﹣4x+2y=0的圆心（2，﹣1），过（1，1）与（2，﹣1）直线斜率为﹣2，∴过（1，1）切线方程的斜率为，则所求切线方程为y﹣1=（x﹣1），即x﹣2y+1=0．故答案为x﹣2y+1=0．三．解答题：要求写出计算或证明步骤（本大题共6小题，共70分，写出证明过程或演算步骤）17．（10分）（2017春•南涧县校级月考）求值：（I）；（II）．【解答】解：（Ⅰ）===；（Ⅱ）==lg1=0．18．（12分）（2017春•南涧县校级月考）设A={x2﹣8x+15=0}，B={x|ax﹣1=0}，若B⊆A，求实数a组成的集合，并写出它的所有非空真子集．【解答】解：A={x2﹣8x+15=0}={3，5}，由题意，当a=0时，B=∅，满足B⊆A，当a≠0，B={}，又A={3，5}，B⊆A，此时或5，则有a=或a=．∴实数a组成的集合为{0，，}所有非空真子集：{0}，{}，{}，{0，}，{0，}，{，}．19．（12分）（2013秋•白城期末）已知函数f（x）=log a（a x﹣1）（a＞0，a≠1）．（1）求函数f（x）的定义域；（2）讨论函数f（x）的单调性．【解答】解：（1）由a x﹣1＞0，得a x＞1．（1分）当a＞1时，x＞0；（2分）当0＜a＜1时，x＜0．（3分）所以f（x）的定义域是当a＞1时，x∈（0，+∞）；当0＜a＜1时，x∈（﹣∞，0）．（4分）（2）当a＞1时，任取x1、x2∈（0，+∞），且x1＜x2，（5分）则，所以．（6分）因为a＞1，所以，即f（x1）＜f（x2）．（8分）故当a＞1时，f（x）在（0，+∞）上是增函数．（9分）当0＜a＜1时，任取x1、x2∈（﹣∞，0），且x1＜x2，（10分）则，所以．（11分）因为0＜a＜1，所以，即f（x1）＜f（x2）．（13分）故当0＜a＜1时，f（x）在（﹣∞，0）上也是增函数．（14分）20．（12分）（2014春•鹰潭期末）求经过两条直线l1：x+y﹣4=0和l2：x﹣y+2=0的交点，且分别与直线2x﹣y﹣1=0（1）平行的直线方程；（2）垂直的直线方程．【解答】解：联立，解得，（1）由平行关系设所求直线的方程为2x﹣y+c=0代入点（1，3）可得2×1﹣3+c=0，解得c=1故所求直线方程为2x﹣y+1=0（2）由垂直关系设所求直线的方程为x+2y+d=0代入点（1，3）可得1+2×3+d=0，解得d=﹣7故所求直线方程为x+2y﹣7=0．21．（12分）（2017春•南涧县校级月考）m为何值时，方程x2+y2﹣4x+2my+2m2﹣2m+1=0表示圆，并求半径最大时圆的方程．【解答】解：方程x2+y2﹣4x+2my+2m2﹣2m+1=0 即（x﹣2）2+（y+m）2=﹣m2+2m+3，它表示圆时，应有﹣m2+2m+3＞0，求得﹣1＜m＜3．当半径最大时，应有﹣m2+2m+3最大，此时，m=1，圆的方程为x2+y2﹣4x+2y+1=0．22．（12分）（2003•北京）某租赁公司拥有汽车100辆．当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．（Ⅰ）当每辆车的月租金定为3600元时，能租出多少辆车？（Ⅱ）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？【解答】解：（Ⅰ）当每辆车的月租金定为3600元时，未租出的车辆数为，所以这时租出了88辆车．（Ⅱ）设每辆车的月租金定为x元，则租赁公司的月收益为，整理得．所以，当x=4050时，f（x）最大，最大值为f（4050）=307050，即当每辆车的月租金定为4050元时，租赁公司的月收益最大，最大月收益为307050元．参与本试卷答题和审题的老师有：沂蒙松；zlzhan；maths；qiss；caoqz；lcb001；wodeqing；zhiyuan；sxs123；刘长柏；lily2011；lincy；ying_0011（排名不分先后）122017年5月8日。