解二元一次方程组l练习题

二元一次方程组的练习题一、选择题1. 已知方程组 $\begin{cases} 2x + 3y = 7 \\ 4x y = 5\end{cases}$，则 $x$ 的值为（）A. 1B. 2C. 3D. 42. 下列方程组中，是二元一次方程组的是（）A. $\begin{cases} x^2 + y = 1 \\ 2x y = 3 \end{cases}$B. $\begin{cases} x + y = 4 \\ 3x 2y = 7 \end{cases}$C. $\begin{cases} x + 2y = 5 \\ x^2 + y^2 = 10\end{cases}$D. $\begin{cases} x + y = 6 \\ 2x + 3y = 8 \end{cases}$3. 解方程组 $\begin{cases} 3x + 5y = 16 \\ 2x 3y = 7\end{cases}$，得到 $x$ 的值为（）A. 2B. 3C. 4D. 5二、填空题1. 方程组 $\begin{cases} 2x + 3y = 9 \\ 4x y = 11\end{cases}$ 的解为 $x=$ ______，$y=$ ______。

2. 若方程组 $\begin{cases} x + y = a \\ 2x y = b\end{cases}$ 的解为 $x=3$，$y=1$，则 $a=$ ______，$b=$ ______。

三、解答题1. 解方程组 $\begin{cases} 5x + 3y = 14 \\ 2x 3y = 8\end{cases}$。

2. 已知方程组 $\begin{cases} 3x + 4y = 10 \\ 2x y = 5\end{cases}$ 的解为 $x=2$，求 $y$ 的值。

3. 某商店进了甲、乙两种商品，甲种商品每件进价80元，乙种商品每件进价50元。

二元一次方程组练习题100道二元一次方程组练题100道（卷一）（范围：代数：二元一次方程组）一、判断1.判断以下方程组是否是方程组y5=26的解：x-3y=1x+2y=3改写：判断以下方程组是否是方程组y=5/26的解：x-3y=1x+2y=32.判断以下方程组是否是方程3x-2y=13的一个解：y=1-x3x+2y=5改写：判断以下方程组是否是方程3x-2y=13的一个解：y=1-x3x+2y=53.由两个二元一次方程组成方程组一定是二元一次方程组。

改写：错误，没有必要改写。

4.判断以下方程组是否可以转化为（2y-3)x+6y=-27x+8：2y-3x=45x+3y=2改写：判断以下方程组是否可以转化为（2y-3)x+6y=-27x+8：2y-3x=45x+3y=25.若(a^2-1)x^2+(a-1)x+(2a-3)y=0是二元一次方程，则a的值为±1.改写：若(a^2-1)x^2+(a-1)x+(2a-3)y=0是二元一次方程，则a的值为±1.6.若x+y=0，且|x|=2，则y的值为2.改写：若x+y=0，且|x|=2，则y的值为-2.7.判断以下方程组是否有唯一的解，若有，则m的值为m≠-5：mx+my=m-3x4x+10y=8改写：判断以下方程组是否有唯一的解，若有，则m的值为m≠-5：mx+my=m-3x4x+10y=88.判断以下方程组是否有无数多个解：x+y=23x+y=6改写：判断以下方程组是否有无数多个解：x+y=23x+y=69.判断以下方程是否有5组整数解：x+y=5x|<5.|y|<5改写：判断以下方程是否有5组整数解：x+y=55<x<5.-5<y<510.判断以下方程组是否是方程x+5y=3的解，反过来方程x+5y=3的解：3x-y=1x+5y=3改写：判断以下方程组是否是方程x+5y=3的解，反过来方程x+5y=3的解：3x-y=1x+5y=311.若|a+5|=5，a+b=1，则a的值为-2.改写：若|a+5|=5，a+b=1，则a的值为-2.12.在方程4x-3y=7里，如果用x的代数式表示y，则x=7+3y/4.改写：在方程4x-3y=7里，如果用x的代数式表示y，则x=7+3y/4.二、选择：13.任何一个二元一次方程都有无数多个解。

二元一次方程组练习题多篇二元一次方程组练习题11)66x+17y=396725x+y=1200答案：x=48y=47(2)18x+23y=230374x-y=1998答案：x=27y=79(3)44x+90y=779644x+y=3476答案：x=79y=48(4)76x-66y=408230x-y=2940答案：x=98y=51(5)67x+54y=854671x-y=5680答案：x=80y=59(6)42x-95y=-141021x-y=1575答案：x=75y=48(7)47x-40y=85334x-y=2006答案：x=59y=48 (8)19x-32y=-1786 75x+y=4950答案：x=66y=95 (9)97x+24y=7202 58x-y=2900答案：x=50y=98 (10)42x+85y=6362 63x-y=1638答案：x=26y=62 (11)85x-92y=-2518 27x-y=486答案：x=18y=44 (12)79x+40y=2419 56x-y=1176答案：x=21y=19 (13)80x-87y=2156 22x-y=880答案：x=40y=12 (14)32x+62y=513457x+y=2850答案：x=50y=57(15)83x-49y=8259x+y=2183答案：x=37y=61(16)91x+70y=584595x-y=4275答案：x=45y=25(17)29x+44y=528188x-y=3608答案：x=41y=93(18)25x-95y=-435540x-y=2000答案：x=50y=59(19)54x+68y=328478x+y=1404答案：x=18y=34(20)70x+13y=352052x+y=2132答案：x=41y=50二元一次方程组练习题2实际问题与二元一次方程组题型归纳知识点一：列方程组解应用题的基本思想找出题目中的等式关系。

初中数学二元一次方程组经典练习题（含答案）解下列二元一次方程组：1. {x +y = 2 3x +7y =10；2.{x +3y = 810x −y =18；3.{3x +2y =1364x −3y =1；4.{ x+52+y−43=2x+20.3−y+70.4= −10 ；5.{ 4x −3y =−1 x 5=y 7 ；6. {3（x +2）=2（y +3）4（x −2）=3（y −3）；7.{ x 5+y 7=10 x 3−y 4=3；8.{x 2+y 3=42x +7y =50 ；9.{12（x +3）+13（y −4）=52（x −3）+5（y +4）=70 ；10.{0.2x +0.5y =9x+22+y+105=15 ；11.{4（x −1） +3（y +1） =320%（x +1）+80%（y −1）=−3；12.{x+2y 2 +x−2y 3 = 113（x +2y ）−4（x −2y ）=30 ；参考答案1. {x +y = 23x +7y =10 ；解： {x +y = 2−−−−−−①3x +7y =10−−−−②①×3，得3x+3y=6-------③②－③，得4y=4，即y=1将y=1代入①，解得x=1故原方程组的解是： {x =1y =12.{x +3y = 810x −y =18； 解：{x +3y = 8−−−−−−−①10x −y =18−−−−−−②②×3，得 30x-3y=54----③①+③，得31x=62，即x=2将x=2代入①，得2+3y=8，y=2故原方程组的解是： {x =2y =23.{3x +2y =1364x −3y =1； 解：{3x +2y =136−−−−−−①4x −3y =1−−−−−−② ①×3，得9x+6y= 132------③ ②×2，得8x-6y=2-----④③+④，得17x= 172 ，x= 12 将x= 12代入②，2-3y=1，y= 13 故原方程组的解是： {x = 12y = 134.{ x+52+y−43=2 x+20.3−y+70.4= −10； 解：{ x+52+y−43=2 −−−−−−−① x+20.3−y+70.4= −10−−−−−−②①等号两边同时乘以6，得3（x+5）+2（y-4）=123x+15+2y-8=12整理，得3x+2y=5----------③②等号两边同时乘以0.3×0.4，得0.4（x+2）-0.3（y+7）=-1.2两边同时乘以10，得4（x+2）-3（y+7）=-124x+8-3y-21=-12整理，得4x-3y=1--------④③×3，得9x+6y=15------⑤④×2，得8x-6y=2-------⑥⑤+⑥，得17x=17，即x=1将x=1代入③，得3+2y=5，y=1故原方程组的解是： {x =1y =15.{ 4x −3y =−1 x 5=y 7 ； 解：{ 4x −3y =−1 −−−−−−−−−−−① x 5=y 7−−−−−−−−−−−−−−−② ②变化为x= 57 y--------------③ 将③代入①，得4×57y -3y=-1 20−217 y =-1，整理得y=7将y=7代入③，得x= 57 ×7，x=5 故原方程组的解是： {x =5y =76. {3（x +2）=2（y +3）4（x −2）=3（y −3）； 解：{3（x +2）=2（y +3）4（x −2）=3（y −3）方程组去括号，得{3x +6=2y +64x −8=3y −9整理得{3x −2y =0−−−−①4x −3y +1=0−−②①×3，得9x-6y=0--------③②×2, 得8x-6y+2=0------④③-④，得x-2=0，即x=2将x=2代入①，得6-2y=0，y=3故原方程组的解是： {x =2y =37.{ x 5+y 7=10 x 3−y 4=3； 解：{ x 5+y 7=10 x 3−y 4=3 方程组去分母，得{ 7x +5y =350−−−−−−①4x −3y =36−−−−−−−②①×3，得21x+15y=1050---③②×5，得20x-15y=180----④③+④，得41x=1230，即x=30将x=30代入①，得210+5y=350，y=28故原方程组的解是： {x =30y =288.{x 2+y 3=4 2x +7y =50； 解：{x 2+y 3=4 2x +7y =50方程组去分母，得{3x +2y =24−−−−−−−① 2x +7y =50−−−−−−−②①×2，得6x+4y=48-----③②×3，得6x+21y=150---④④-③，得17y=102，即y=6将y=6代入① ，得3x+12=24，x=4故原方程组的解是： {x =4y =69.{12（x +3）+13（y −4）=52（x −3）+5（y +4）=70 ； 解：{12（x +3）+13（y −4）=5−−−−① 2（x −3）+5（y +4）=70−−−②①去分母，得3（x+3）+2（y-4）=30去括号，得3x+9+2y-8=30整理，得3x+2y-29=0-----------③②去括号，得2x-6+5y+20=70整理，得2x+5y-56=0-----------④③×2，得6x+4y-58=0------------⑤④×3，得6x+15y-168=0----------⑥⑥-⑤，得11y-110=0，即y=10将y=10代入③，得3x+20-29=0，x=3故原方程组的解是：{x=3 y=1010.{0.2x+0.5y=9x+2 2+y+105=15 ；解：{0.2x+0.5y=9−−−−−①x+22+y+105=15−−−−−−②①等号两边同时乘以10，得2x+5y=90------------------③②去分母，得5（x+2）+2（y+10）=150去括号，整理得5x+2y=120---④③×5，得10x+25y=450------⑤④×2，得10x+4y=240-------⑥⑤-⑥，得21y=210，即y=10将y=10代入③，得2x+50=90，x=20故原方程组的解是：{x=20 y=1011.{4（x −1） +3（y +1） =320%（x +1）+80%（y −1）=−3； 解：{4（x −1） +3（y +1） =3−−−−−−−−−①20%（x +1）+80%（y −1）=−3−−−−−−② ①去括号，得4x-4+3y+3=3，整理得4x+3y=4-----③ ②去百分号，得0.2（x+1）+0.8（y-1）=-3等号两边同时乘以10，得2（x+1）+8（y-1）=-30 去括号，得2x+2+8y-8=-30，整理得x+4y=-12----④ ④×4，得4x+16y=-48------------------------⑤ ⑤-③，得13y=-52，即y=-4将y=-4代入④，得x-16=-12，x=4故原方程组的解是： {x =4y =−412.{x+2y 2 +x−2y 3 = 11 3（x +2y ）−4（x −2y ）=30； 解：{x+2y 2 +x−2y 3 = 11 −−−−−−−−−−−−−−① 3（x +2y ）−4（x −2y ）=30−−−−−−② ①×6，得3（x+2y ）+2（x-2y ）=66----------------③③-②，得6（x-2y ）=36，即x-2y= 6 -------④①×12，得6（x+2y ）+4（x-2y ）=132---------------⑤⑤+②，得9（x+2y）=162，即x+2y=18---⑥④+⑥，得2x=24，即x=12④-⑥，得-4y=-12，即y=3故原方程组的解是：{x=12 y=3。

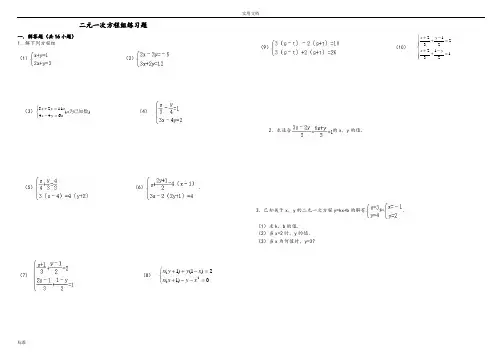
实用文档标准二元一次方程组练习题一．解答题（共16小题） 1．解下列方程组 （1）（2）（3）)(6441125为已知数a a y x ay x ⎩⎨⎧=-=+ （4）（5）（6）．（7）（8）⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x（9）（10） ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2．求适合的x ，y 的值．3．已知关于x ，y 的二元一次方程y=kx+b 的解有和．（1）求k ，b 的值．（2）当x=2时，y 的值． （3）当x 为何值时，y=3？1．解下列方程组（1）（2）；（3）；（4）（5）．（6）（7）（8）（9）（10）；2．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解.word版本二元一次方程组解法练习题精选参考答案与试题解析一．解答题（共16小题）1．求适合的x，y的值．考点：解二元一次方程组．分析：先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法消去未知数x，求出y的值，继而求出x的值．解答：解：由题意得：，由（1）×2得：3x ﹣2y=2（3），由（2）×3得：6x+y=3（4），（3）×2得：6x﹣4y=4（5），（5）﹣（4）得：y=﹣，把y的值代入（3）得：x=，∴．点评：本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法．2．解下列方程组（1）（2）（3）（4）．考点：解二元一次方程组．分析：（1）（2）用代入消元法或加减消元法均可；（3）（4）应先去分母、去括号化简方程组，再进一步采用适宜的方法求解．解答：解：（1）①﹣②得，﹣x=﹣2，解得x=2，把x=2代入①得，2+y=1，解得y=﹣1．故原方程组的解为．（2）①×3﹣②×2得，﹣13y=﹣39，解得，y=3，把y=3代入①得，2x﹣3×3=﹣5，解得x=2．故原方程组的解为．（3）原方程组可化为，①+②得，6x=36，x=6，①﹣②得，8y=﹣4，y=﹣．所以原方程组的解为．（4）原方程组可化为：，①×2+②得，x=，把x=代入②得，3×﹣4y=6，y=﹣．所以原方程组的解为．点评：利用消元法解方程组，要根据未知数的系数特点选择代入法还是加减法：①相同未知数的系数相同或互为相反数时，宜用加减法；②其中一个未知数的系数为1时，宜用代入法．3．解方程组：考点：解二元一次方程组．word版本专题：计算题．分析：先化简方程组，再进一步根据方程组的特点选用相应的方法：用加减法．解答：解：原方程组可化为，①×4﹣②×3，得7x=42，解得x=6．把x=6代入①，得y=4．所以方程组的解为．点评：；二元一次方程组无论多复杂，解二元一次方程组的基本思想都是消元．消元的方法有代入法和加减法．4．解方程组：考点：解二元一次方程组．专题：计算题．分析：把原方程组化简后，观察形式，选用合适的解法，此题用加减法求解比较简单．解答：解：（1）原方程组化为，①+②得：6x=18，∴x=3．代入①得：y=．所以原方程组的解为．点评：要注意：两个二元一次方程中同一未知数的系数相反或相等时，把这两个方程的两边相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法．本题适合用此法．5．解方程组：考点：解二元一次方程组．专题：计算题；换元法．分析：本题用加减消元法即可或运用换元法求解．解答：解：，①﹣②，得s+t=4，①+②，得s﹣t=6，即，解得．所以方程组的解为．点评：此题较简单，要熟练解方程组的基本方法：代入消元法和加减消元法．6．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？考点：解二元一次方程组．专题：计算题．分析：（1）将两组x ，y 的值代入方程得出关于k、b的二元一次方程组，再运用加减消元法求出k、b的值．（2）将（1）中的k、b代入，再把x=2代入化简即可得出y的值．（3）将（1）中的k、b和y=3代入方程化简即可得出x的值．解答：解：（1）依题意得：①﹣②得：2=4k，所以k=，所以b=．（2）由y=x+，把x=2代入，得y=．word 版本（3）由y=x+把y=3代入，得x=1．点评：本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的代入，可得出要求的数．7．解方程组：（1）；（2）．考点：解二元一次方程组．分析：根据各方程组的特点选用相应的方法：（1）先去分母再用加减法，（2）先去括号，再转化为整式方程解答．解答：解：（1）原方程组可化为，①×2﹣②得：y=﹣1，将y=﹣1代入①得：x=1．∴方程组的解为；（2）原方程可化为，即，①×2+②得：17x=51，x=3，将x=3代入x﹣4y=3中得：y=0．∴方程组的解为．点评：这类题目的解题关键是理解解方程组的基本思想是消元，掌握消元的方法有：加减消元法和代入消元法．根据未知数系数的特点，选择合适的方法．8．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题应把方程组化简后，观察方程的形式，选用合适的方法求解．解答：解：原方程组可化为，①+②，得10x=30，x=3，代入①，得15+3y=15，y=0．则原方程组的解为．点评：解答此题应根据各方程组的特点，有括号的去括号，有分母的去分母，然后再用代入法或加减消元法解方程组．9．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题为了计算方便，可先把（2）去分母，然后运用加减消元法解本题．解答：解：原方程变形为：，两个方程相加，得4x=12，x=3．把x=3代入第一个方程，得4y=11，y=．解之得．点评：本题考查的是二元一次方程组的解法，方程中含有分母的要先化去分母，再对方程进行化简、消元，即可解出此类题目．word版本10．解下列方程组：（1）（2）考点：解二元一次方程组．专题：计算题．分析：此题根据观察可知：（1）运用代入法，把①代入②，可得出x，y的值；（2）先将方程组化为整系数方程组，再利用加减消元法求解．解答：解：（1），由①，得x=4+y③，代入②，得4（4+y ）+2y=﹣1，所以y=﹣，把y=﹣代入③，得x=4﹣=．所以原方程组的解为．（2）原方程组整理为，③×2﹣④×3，得y=﹣24，把y=﹣24代入④，得x=60，所以原方程组的解为．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．11．解方程组：（1）（2）考点：解二元一次方程组．专题：计算题；换元法．分析：方程组（1）需要先化简，再根据方程组的特点选择解法；方程组（2）采用换元法较简单，设x+y=a，x﹣y=b，然后解新方程组即可求解．解答：解：（1）原方程组可化简为，解得．（2）设x+y=a，x﹣y=b，∴原方程组可化为，解得，∴∴原方程组的解为．点评：此题考查了学生的计算能力，解题时要细心．12．解二元一次方程组：（1）；（2）．考点：解二元一次方程组．word版本专题：计算题．分析：（1）运用加减消元的方法，可求出x、y的值；（2）先将方程组化简，然后运用加减消元的方法可求出x、y的值．解答：解：（1）将①×2﹣②，得15x=30，x=2，把x=2代入第一个方程，得y=1．则方程组的解是；（2）此方程组通过化简可得：，①﹣②得：y=7，把y=7代入第一个方程，得x=5．则方程组的解是．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．13．在解方程组时，由于粗心，甲看错了方程组中的a ，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．考点：解二元一次方程组．专题：计算题．分析：（1）把甲乙求得方程组的解分别代入原方程组即可；（2）把甲乙所求的解分别代入方程②和①，求出正确的a、b，然后用适当的方法解方程组．解答：解：（1）把代入方程组，得，解得：．把代入方程组，得，解得：．∴甲把a看成﹣5；乙把b看成6；（2）∵正确的a是﹣2，b是8，∴方程组为，解得：x=15，y=8．则原方程组的解是．点评：此题难度较大，需同学们仔细阅读，弄清题意再解答．14．考点：解二元一次方程组．分析：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可．解答：解：由原方程组，得，由（1）+（2），并解得x=（3），把（3）代入（1），解得y=∴原方程组的解为．点评：用加减法解二元一次方程组的一般步骤：1．方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去乘方程的两边，使一个未知数的系数互为相反数或相等；word版本2．把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；3．解这个一元一次方程；4．将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解．15．解下列方程组：（1）；（2）．考点：解二元一次方程组．分析：将两个方程先化简，再选择正确的方法进行消元．解答：解：（1）化简整理为，①×3，得3x+3y=1500③，②﹣③，得x=350．把x=350代入①，得350+y=500，∴y=150．故原方程组的解为．（2）化简整理为，①×5，得10x+15y=75③，②×2，得10x﹣14y=46④，③﹣④，得29y=29，∴y=1．把y=1代入①，得2x+3×1=15，∴x=6．故原方程组的解为．点评：方程组中的方程不是最简方程的，最好先化成最简方程，再选择合适的方法解方程．16．解下列方程组：（1）（2）考点：解二元一次方程组．分析：观察方程组中各方程的特点，用相应的方法求解．解答：解：（1）①×2﹣②得：x=1，将x=1代入①得：2+y=4，y=2．∴原方程组的解为；（2）原方程组可化为，①×2﹣②得：﹣y=﹣3，y=3．将y=3代入①得：x=﹣2．∴原方程组的解为．点评：解此类题目要注意观察方程组中各方程的特点，采用加减法或代入法求解．word版本。

二元一次方程组求解方法练习题30道1. 解方程⚪1：已知方程组$$\begin{cases}2x + 3y = 7 \\3x - 5y = -1\end{cases}$$求 $x$ 和 $y$ 的值。

<details><summary>点击查看解答</summary>首先，我们可以使用消元法解这个方程组。

1. 对第一个方程乘以2，得到 $4x + 6y = 14$。

2. 对第二个方程乘以3，得到 $9x - 15y = -3$。

现在，我们将这两个方程相加，消去$x$的项：$$(4x + 6y) + (9x - 15y) = 14 - 3$$化简得：$13x - 9y = 11$。

现在，我们可以解得 $x = \frac{11+9y}{13}$。

接下来，将 $x$ 的值代入第一个方程：$$2 \cdot \left(\frac{11+9y}{13}\right) + 3y = 7$$化简得：$4y^2 - 5y - 2 = 0$。

解这个二次方程，可以得到 $y$ 的两个值：$y = 1$ 或 $y = -\frac{1}{4}$。

将 $y$ 的值代入 $x$ 的表达式，可以得到对应的 $x$ 值。

因此，方程组的解为：$(x, y) = \left(\frac{20}{13}, 1\right)$ 或 $\left(-\frac{3}{13}, -\frac{1}{4}\right)$。

</details>2. 解方程⚪2：已知方程组$$\begin{cases}x + 3y = 5 \\2x - 4y = 10\end{cases}$$求 $x$ 和 $y$ 的值。

<details><summary>点击查看解答</summary>我们可以使用消元法解这个方程组。

首先，将第一个方程乘以2，得到 $2x + 6y = 10$。

二元一次方程组解法练习题精选（含答案）一．解答题（共16小题）．求适合的值．y，1x的．解下列方程组2（1））2（（3）．）4（3．解方程组：4．解方程组：5．解方程组：y=kx+by．已知关于x，的二元一次方程的解有．和6 的值．，）求（1kb 时，x=2）当（2y的值．）当（3y=3为何值时，x？7．解方程组：）；（1．（2 ）．解方程组：89．解方程组：．解下列方程组：10（1））2 （11．解方程组：）（1）2 （．解二元一次方程组：12；）1（．）．（2而得解为，，由于粗心，13．在解方程组甲看错了方程组中的a 时，，而得解为．乙看错了方程组中的b（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．．1415．解下列方程组：）；1（）．2（）2 ）（（16．解下列方程组：1x?y?25?的解是否满足2x－y=8？满足方程组17.2x－y=8的一对x，的值是否是方程y?8y??x2?25?x?y?组的解？?8?y?x2?二元一次方程组解法练习题精选（含答案）参考答案与试题解析一．解答题（共16小题）．求适合的x，y的值．1考解二元一次方程组．809625点：分，然后在用加减消，得到一组新的方程先把两方程变形（去分母）析：的值．的值，继而求出，求出yx元法消去未知数x解，解：由题意得：答：3），2y=22由（1）×得：3x﹣（6x+y=3）由（2×3得：（4），），54y=46x）（3×2得：﹣（，）得：4y=﹣）﹣（（5的值代入（把y3，）得：x=∴．本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法．点评：．解下列方程组2．）（12）（（3）．）4 （解二元一次方程组．809625 考点：（1）（2）用代入消元法或加减消元法均可；分析：（3）（4）应先去分母、去括号化简方程组，再进一步采用适宜的方法求解．解解：（1）①﹣②得，﹣x=﹣2，答：解得x=2，把x=2代入①得，2+y=1，解得y=﹣1．故原方程组的解为．39，得，﹣﹣②×213y=﹣3（2）①×y=3，解得，5，﹣﹣代入y=3①得，2x3×3=把．解得x=2故原方程组的解为．，）原方程组可化为3（．①+②得，6x=36，x=6，①﹣②得，8y=﹣4，﹣．y=所以原方程组的解为．）原方程组可化为：（4，，得，x=①×2+②4y=6得，x=代入②3，×﹣把y=．﹣．所以原方程组的解为利用消元法解方程组，要根据未知数的系数特点选择代入法还是加减法：点评：①相同未知数的系数相同或互为相反数时，宜用加减法；②其中一个未知数的系数为1时，宜用代入法．．解方程组：3809625 解二元一次方程组．考：点计算题．专：题先化简方程组，再进一步根据方程组的特点选用相应的方法：用加减法．分．析：解解：原方程组可化为，答：3，得①×4﹣②×7x=42，．解得x=6 ．x=6代入①，得y=4把．所以方程组的解为注意：二元一次方程组无论多复杂，解二元一次方程组的基本思想都是消点评：元．消元的方法有代入法和加减法．．解方程组：4809625 考解二元一次方程组．：点计算题．专：题把原方程组化简后，观察形式，选用合适的解法，此题用加减法求解比较分析：简单．解，）原方程组化为1（解：答：得：6x=18，②①+ x=3∴．．y=得：①代入．所以原方程组的解为．要注意：两个二元一次方程中同一未知数的系数相反或相等时，把这两个点评：方程的两边相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法．本题适合用此法．．解方程组：5考解二元一次方程组．809625点：专计算题；换元法．题：分本题用加减消元法即可或运用换元法求解．析：解解：，答：s+t=4，，得①﹣②，s，得﹣t=6①+②，即解得．．所以方程组的解为点此题较简单，要熟练解方程组的基本方法：代入消元法和加减消元法．评：和．的解有，y的二元一次方程y=kx+b 6．已知关于x 的值．1）求k，b（的值．）当x=2时，y（2 y=3）当x为何值时，？（3 考解二元一次方程组．809625：点计算题．专题：的二元一次方程组b，的值代入方程得出关于k、（1）将两组x，y分析：再运用加减消元法求出k、b的值．（2）将（1）中的k、b代入，再把x=2代入化简即可得出y的值．（3）将（1）中的k、b和y=3代入方程化简即可得出x的值．解解：）依题意得：（1 答：①﹣②得：2=4k，k=，所以b=．所以x+，2）由y=（y=．代入，得x=2把x+）由y=3（．x=1代入，得y=3把点本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的评：代入，可得出要求的数．7．解方程组：）；（1）．2 （考解二元一次方程组．809625点：分根据各方程组的特点选用相应的方法：（（）先2）先去分母再用加减法，1 去括号，再转化为整式方程解答．析：解解：（1）原方程组可化为，答：①×2②得：﹣，y=﹣1 ①得：1将y=﹣代入．x=1方程组的解为；∴2（）原方程可化为，，即①×得：②2+ ，17x=51．x=3，将x=3代入x﹣4y=3中得：y=0．方程组的解为．∴这类题目的解题关键是理解解方程组的基本思想是消元，掌握消元的方法点评：有：加减消元法和代入消元法．根据未知数系数的特点，选择合适的方法．．解方程组：8考解二元一次方程组．809625点：专计算题．题：分本题应把方程组化简后，观察方程的形式，选用合适的方法求解．析：解解：原方程组可化为，答：①+②，得10x=30，x=3，代入①，得15+3y=15，y=0．则原方程组的解为．解答此题应根据各方程组的特点，有括号的去括号，有分母的去分母，然点．评：后再用代入法或加减消元法解方程组．．解方程组：9解二元一次方程组．809625 考：点计算题．专题：分本题为了计算方便，可先把（2）去分母，然后运用加减消元法解本题．析：解解：原方程变形为：，答：两个方程相加，得4x=12，x=3．把x=3代入第一个方程，得，4y=11．y=解之得．本题考查的是二元一次方程组的解法，方程中含有分母的要先化去分母，点评：再对方程进行化简、消元，即可解出此类题目．．解下列方程组：10．）1（）2 （解二元一次方程组．809625 考：点计算题．专：题此题根据观察可知：分析：（1）运用代入法，把①代入②，可得出x，y的值；（2）先将方程组化为整系数方程组，再利用加减消元法求解．解，）1（解：答：③，①由，得x=4+y ，，得代入②4（4+y）+2y=﹣1﹣y=，所以﹣．=把y=代入﹣③，得x=4所以原方程组的解为．，（2）原方程组整理为24，﹣，得④×2③×﹣3y= 把y=，，得④代入﹣24x=60．所以原方程组的解为点此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目评：的训练达到对知识的强化和运用．11．解方程组：）（1）（2解二元一次方程组．809625 考：点计算题；换元法．专：题方程组（1分）需要先化简，再根据方程组的特点选择解法；析：方程组（2）采用换元法较简单，设x+y=a，x﹣y=b，然后解新方程组即可求解．解）原方程组可化简为，（解：1答：解得．﹣，）设（2x+y=axy=b，，∴原方程组可化为，解得．∴原方程组的解为∴．点此题考查了学生的计算能力，解题时要细心．评：12．解二元一次方程组：）；（1．）（2解二元一次方程组．考809625点：计算题．专：题（1）运用加减消元的方法，可求出x、y分的值；析：（2）先将方程组化简，然后运用加减消元的方法可求出x、y的值．解解：（1）将①×2﹣②，得答：15x=30，x=2，把x=2代入第一个方程，得y=1．则方程组的解是；，）此方程组通过化简可得：2（．①﹣②得：y=7，把y=7代入第一个方程，得x=5．则方程组的解是．此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目点评：的训练达到对知识的强化和运用．而得解为，a，．在解方程组时，由于粗心，甲看错了方程组中的13，而得解为b乙看错了方程组中的．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．考解二元一次方程组．809625点：专计算题．题：分（1）把甲乙求得方程组的解分别代入原方程组即可；析：（2）把甲乙所求的解分别代入方程②和①，求出正确的a、b，然后用适当的方法解方程组．解代入方程组，（解：1）把答：，得．解得：代入方程组，把得，解得：．∴甲把a看成﹣5；乙把b看成6；（2）∵正确的a是﹣2，b是8，方程组为，∴．解得：x=15，y=8．则原方程组的解是点此题难度较大，需同学们仔细阅读，弄清题意再解答．评：．14考809625 解二元一次方程组．点：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可．分析：解解：由原方程组，得答：，1由（）2（+），并解得，）3（x=把（3）代入（1），解得y=，原方程组的解为．∴用加减法解二元一次方程组的一般步骤：点评：1．方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去乘方程的两边，使一个未知数的系数互为相反数或相等；2．把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；3．解这个一元一次方程；4．将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解．15．解下列方程组：）；（1）（2．809625 考解二元一次方程组．点：分将两个方程先化简，再选择正确的方法进行消元．析：1解：（）化简整理为，解，③3x+3y=1500，得3①×答：②﹣③，得x=350．把x=350代入①，得350+y=500，∴y=150．故原方程组的解为．）化简整理为，（2①×5，得10x+15y=75③，②×2，得10x﹣14y=46④，③﹣④，得29y=29，∴y=1．把y=1代入①，得2x+3×1=15，∴x=6．故原方程组的解为．点方程组中的方程不是最简方程的，最好先化成最简方程，再选择合适的方评：法解方程．）（216．解下列方程组：（1）考解二元一次方程组．809625点：分观察方程组中各方程的特点，用相应的方法求解．析：解解：（1）①×2﹣②得：x=1，得：①代入x=1将答：2+y=4，y=2．原方程组的解为；∴）原方程组可化为，（2①×2﹣②得：﹣y=﹣3，y=3．将y=3代入①得：x=﹣2．原方程组的解为．∴点解此类题目要注意观察方程组中各方程的特点，采用加减法或代入法求解．评：。

解二元一次方程50道练习题(带答案)
1. 解方程组：
{2x - y = 3
{3x + 2y = 8
解答：
首先，可以通过消元法来解决这个问题。

将第一个方程乘以2，并将第二个方程乘以3，得到：
{4x - 2y = 6
{9x + 6y = 24
接下来，将第一个方程的两倍加到第二个方程上，得到：
{4x - 2y = 6
{13x + 4y = 30
然后，将第一个方程的2倍加到第二个方程上，得到：
{4x - 2y = 6
{8x - 8y = 12
接下来，将第二个方程的两倍加到第一个方程上，得到：
{36x = 18
{8x - 8y = 12
最后，解方程得到：
{x = 0.5
{y = 2
2. 解方程组：
{3x + 2y = 7
{5x + 3y = 11
解答：
可以使用消元法来解决这个方程组。

将第一个方程乘以3，并将第二个方程乘以2，得到：
{9x + 6y = 21
{10x + 6y = 22
接下来，将第二个方程的两倍减去第一个方程，得到：
{9x + 6y = 21
{2x = 1
最后，解方程得到：
{x = 0.5
{y = 2
3. ...
...
50. ...
...
这是前面五道解二元一次方程的练习题，你可以根据相同的方法解答剩下的题目。

希望这些练习题对你有帮助！。

二元一次方程组解法练习题精选(含答案) 二元一次方程组解法练题精选（含答案）一．解答题（共16小题）1.求适合 $3x-2y=2$ 和 $6x+y=3$ 的 $x$，$y$ 的值。

解答：由 $(1)\times2$ 得：$3x-2y=2$（3），由$(2)\times3$ 得：$6x+y=3$（4），$(3)\times2$ 得：$6x-4y=4$（5），$(5)-(4)$ 得：$y=-\frac{1}{2}$，把 $y$ 的值代入 $(3)$ 得：$x=\frac{1}{2}$，故原方程组的解为$(x,y)=(\frac{1}{2},-\frac{1}{2})$。

2.解下列方程组：begin{cases} \frac{x}{2}+\frac{y}{3}=1 \\\frac{x}{3}+\frac{y}{2}=2 \end{cases}$$解答：由题意得：$\frac{x}{2}+\frac{y}{3}=1$（1），$\frac{x}{3}+\frac{y}{2}=2$（2），先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法解二元一次方程组。

把 $(1)\times3$ 减去 $(2)\times2$，得到 $x=-1$，把$x=-1$ 代入 $(1)$，得到 $y=6$，故原方程组的解为 $(x,y)=(-1,6)$。

3.解方程组：begin{cases} 3x+2y=7 \\ 2x+3y=8 \end{cases}$$解答：把两方程相加得到 $5x+5y=15$，即 $x+y=3$，把$x+y=3$ 代入其中一个方程，如 $(1)$，得到 $x=-1$，再把$x=-1$ 代入 $(1)$ 或 $(2)$ 中的一个方程，如 $(1)$，得到$y=4$，故原方程组的解为 $(x,y)=(-1,4)$。

4.解方程组：begin{cases} x+y=5 \\ 2x-y=4 \end{cases}$$解答：把两方程相加得到 $3x=9$，即 $x=3$，把$x=3$ 代入其中一个方程，如 $(1)$，得到 $y=2$，再把 $x=3$，$y=2$ 代入原方程组检验，发现符合，故原方程组的解为$(x,y)=(3,2)$。

二元一次方程组经典练习题+答案解析100道二元一次方程组练题100道（卷一）1、判断1、方程组xy526的解是（）。

解：这不是一个完整的方程组，缺少另一个方程，无法判断解。

2、方程组1是方程组yx3 2的解是方程3x-2y=13的一个解（）。

解：将方程组代入3x-2y=13中，得到3x-2(-x/3-1/2)=13，化简得到x=5，y=-4，代入方程组可验证是解，因此选（√）。

3、由两个二元一次方程组成方程组一定是二元一次方程组（）。

解：不一定，例如x+y=1和2x+2y=2就不是二元一次方程组。

4、方程组x3y 573x2y12235 3可以转化为方程组解：将第一个方程移项得到x+3y=2，代入第二个方程中消去x得到-7y=-18，解得y=18/7，代入第一个方程得到x=-41/7，因此可以转化为方程组5x-6y=-27和2y-3x+4=2，选（√）。

5、若(a-1)x+(a-1)x+(2a-3)y=0是二元一次方程，则a的值为±1（）。

解：将XXX提取出来得到(a-1)(x+y)+(2a-3)y=0，因此x+y=-2a+3y/y-2，这是一个关于a的一次函数，当a=±1时，x+y=±1，此时方程组化为x+y=±1和-2x-2y=0，是二元一次方程组，因此选（√）。

6、若x+y=0，且|x|=2，则y的值为2（）。

解：由x+y=0得到y=-x，代入|x|=2中得到|x|=|x+y|=|-x+y|=2，解得x=±1，因此y=±1，不等于2，选（×）。

7、方程组mx my m3x4x10y8有唯一的解，那么m的值为m≠-5（）。

解：将第一个方程移项得到(m+3)x+my=m，代入第二个方程中消去x得到(3m+2)y=8-m，因为有唯一解，所以3m+2≠0，即m≠-2/3，代入方程组中验证，当m≠-5时，有唯一解，因此选（√）。

8、方程组1x y 233有无数多个解（）。

二元一次方程组解法练习题一．解答题（共16小题） 1．解下列方程组（1） （2）（3）)(6441125为已知数a a y x ay x ⎩⎨⎧=-=+（4）（5）（6）．（7）（8）⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x（9） （10） ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2．求适合的x ，y 的值．3．已知关于x ，y 的二元一次方程y=kx+b 的解有和． （1）求k ，b 的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？1．解下列方程组（1）（2）；（3）；（4）（5）．（6）（7）（8）（9）（10）；2．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解.二元一次方程组解法练习题精选参考答案与试题解析一．解答题（共16小题） 1．求适合的x ，y 的值．2．解下列方程组 （1）（2）（3）（4）．3．解方程组：7．解方程组：（1）；（2）．8．解方程组：9．解方程组：10．解下列方程组：（1）（2）11．解方程组：（1）（2）12．解二元一次方程组：（1）；（2）．13．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．14．15．解下列方程组：（1）；16．解下列方程组：（1）（2）。

二元一次方程组计算题100题1.解方程组：2x+9y=81，3x+y=34.2.解方程组：9x+4y=35，8x+3y=30.3.解方程组：7x+2y=52，7x+4y=62.4.解方程组：4x+6y=54，9x+2y=87.5.解方程组：2x+y=7，2x+5y=19.6.解方程组：x+2y=21，3x+5y=56.7.解方程组：5x+7y=52，5x+2y=22.8.解方程组：5x+5y=65，7x+7y=203.9.解方程组：8x+4y=56，x+4y=21.10.解方程组：5x+7y=41，5x+8y=44.11.解方程组：7x+5y=54，3x+4y=38.12.解方程组：x+8y=15，4x+y=29.13.解方程组：3x+6y=24，9x+5y=46.14.解方程组：9x+2y=62，4x+3y=36.15.解方程组：9x+4y=46，XXX。

16.解方程组：9x+7y=135，4x+y=41.17.解方程组：3x+8y=51，x+6y=27.18.解方程组：9x+3y=99，4x+7y=95.19.解方程组：9x+2y=38，3x+6y=18.20.解方程组：5x+5y=45，7x+9y=69.21.解方程组：8x+2y=28，7x+8y=62.22.解方程组：x+6y=14，3x+3y=27.23.解方程组：7x+4y=67，2x+8y=26.24.解方程组：5x+4y=52，7x+6y=74.25.解方程组：7x+y=9，4x+6y=16.26.解方程组：6x+6y=48，XXX。

27.解方程组：8x+2y=16，7x+y=11.28.解方程组：4x+9y=77，8x+6y=94.29.解方程组：6x+8y=68，7x+6y=66.30.解方程组：2x+2y=22，7x+2y=47.31.解方程组：5x+3y=8，3x+5y=8.32.解方程组：6x-7y=5，x+2y=4.33.解方程组：10x-8y=14，x+y=5.34.解方程组：4x+7y=3，x+y=0.35.解方程组：3x+y=10，7x-y=20.36.解方程组：44x+10y=27，x+y=1.37.解方程组：8x-y=0，x+y=18.38.解方程组：11x-y=12，11y-x=-12.39.解方程组：5x+6y=27，2x+3y=12.40.解方程组：2x+3y=12，7x-2y=4.41.解方程组：2x-5y=0，2x+y=2.42.解方程组：7x-3y=3，3x+2y=21.43.解方程组：7x+2y=21，6x-y=1.54.5x+6y=4805x+3y=240改写：将第一行乘以0.5，得到第二行。

二元一次方程组练习题(含答案) 二元一次方程组练题一．解答题（共16小题）1.解下列方程组：1）x+2y-1=23x-2y=52）1-yx+2/3=1/22y+3=3x3）5x+2y=11a4x-4y=6a4）2x+3y=73x-2y=15）2x-3y=75x+4y=176）2x+3y=13x-2y=57）3x-4y=-12x+5y=138）x(y+1)+y(1-x)=2x(x+1)-y-x^2=09）3x+y=72x-3y=-810）x^2+xy=2y-x+2=02.求适合的x，y的值。

已知关于x，y的二元一次方程y=kx+b的解有和。

1）求k，b的值。

2）当x=2时，y的值。

3）当y=3时，x的值为多少？解答：1.1）将第二个方程变形得到y=(3x-5)/2，代入第一个方程中，得到x=3，y=-2.2）将第一个方程变形得到y=(1/2-1+xy)/x，代入第二个方程中，得到x=3，y=-1.3）将第二个方程变形得到y=x-3/2，代入第一个方程中，得到x=2，y=1.4）将第二个方程变形得到y=(3x-1)/2，代入第一个方程中，得到x=2，y=1.5）将第一个方程变形得到y=(2x-7)/3，代入第二个方程中，得到x=1，y=-1.6）将第二个方程变形得到y=(3x-5)/2，代入第一个方程中，得到x=1，y=-1.7）将第二个方程变形得到y=(3x+1)/4，代入第一个方程中，得到x=5，y=2.8）将第一个方程变形得到y=(2-x^2)/(1-x)，代入第二个方程中，得到x=1，y=1.9）将第二个方程变形得到y=(2x+8)/3，代入第一个方程中，得到x=1，y=1.10）将第一个方程变形得到y=2/x-x，代入第二个方程中，得到x=1，y=0.2.1）由于y=kx+b，所以当x=1时，y=k+b；当x=2时，y=2k+b。

又因为已知y=3时，x的值为多少，所以将y=kx+b代入得到kx+b=3，解得x=(3-b)/k。

二元一次方程组解法练习题精选（含答案）一．解答题（共16小题）1．求适合的x，y的值．2．解下列方程组（1）（2）（3）（4）．3．解方程组：4．解方程组：5．解方程组：6．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？7．解方程组：（1）；（2）．8．解方程组：9．解方程组：10．解下列方程组：（1）（2）11．解方程组：（1）（2）12．解二元一次方程组：（1）；（2）．13．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．14．15．解下列方程组：（1）；（2）．16．解下列方程组：（1）（2）第二十六章《二次函数》检测试题1，（2008年芜湖市）函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是 （ ）2，在一定条件下，若物体运动的路程s （米）与时间t （秒）的关系式为s ＝5t 2+2t ，则当t ＝4时，该物体所经过的路程为（ ）3，已知二次函数y ＝ax 2+bx +c (a ≠0)的图象如图2所示，给出以下结论：① a +b +c ＜0；② a －b +c ＜0；③ b +2a ＜0；④ abc ＞0 .其中所有正确结论的序号是（ ）A. ③④B. ②③C. ①④D. ①②③4，二次函数y ＝ax 2+bx +c 的图象如图3所示，若M ＝4a +2b +c ，N ＝a －b +c ，P ＝4a +2b ，则（ ）A.M ＞0，N ＞0，P ＞0B. M ＞0，N ＜0，P ＞0C. M ＜0，N ＞0，P ＞0D. M ＜0，N ＞0，P ＜05，如果反比例函数y ＝k x的图象如图4所示，那么二次函数y ＝kx 2－k 2x －1的图象大致为（ ）6y 所对应的函数值依次为：20，56，110，182，274，380，506，650.其中有一个值不正确，这个不正确的值是()A. 506B.380C.274D.18图3图4 A ． B ． 图5 图1A. y ＝x 2－2B. y ＝(x －2)2C. y ＝x 2+2D. y ＝(x +2)28如图6，小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数h ＝3.5t －4.9t 2（t 的单位：s ，h 的单位：m ）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（ ）A.0.71sB.0.70sC.0.63sD.0.36s9，如果将二次函数y ＝2x 2的图象沿y 轴向上平移1个单位，那么所得图象的函数解析式是 .10，平移抛物线y ＝x 2+2x －8，使它经过原点，写出平移后抛物线的一个解析式______ .11，若二次函数y ＝x 2－4x ＋c 的图象与x 轴没有交点，其中c 为整数，则c ＝12，二次函数y ＝ax 2+bx +c 的图像如图7所示，则点A (a ，b )在第＿＿＿象限.13，已知抛物线y ＝x 2－6x +5的部分图象如图8，则抛物线的对称轴为直线x ＝ ，满足y ＜0的x 的取值范围是 .14，已知一抛物线与x 轴的交点是)0,2( A 、B （1，0），且经过点C （2，8）。

(7)二元一次方程组练习题一.解答题（共16小题）1.解下列方程组⑴g[2x+y=3 ⑵严一3厂一5l3x+2y-12(3)5x + 2y = 1k?4.v-4y = 6a（a为己知数）(4)pr13耳-4y=2Cx- 1)3 (x-4) =4 (y+2)x+1 y 一TP -=22x- 1 1 ■ y・3亠2 =13耳-2 (2y+l) =4x(y + i) + y(i-x)= 2 x(x +l)-y-x2 =03 (s- t) - 2 (s+t) =103 (s-t) +2 (s+t) =26(10)2.求适令¥号jx,心.3.已知关于x, y的二元一次方程y二kx+b的解有(沪彳和［沪一1尸4 (尸2(1) 求k, b的值.(2) 当x=2时.y的值.(3) 当x为何值吋，y=31.解下列方程组J9x+2y=20|.3x+4y=10：<+7=1(6) | 3 53 (x+y) +2 (x-3y) =15x+4y=14(7) ( x- 3 _ y~ 3_ 13 =124 (x+y) -5 (x -y) =2x - 7=44x+2y= 一 1f3x-2 (x+2y)二3 [llx+4 Cx+2y)二452 _ y_ 7 :5刁Fx-2 "T" 5 - yI-"1fx+y=l|.20%x+30%y=25%X22.在解方程组f ax+5y=104K -by= - 4 时，由于粗心，甲看错了方程组中的a,而得解为3],乙看错了方程组中的b,而得解为丫x=5(1)甲把a看成了什么，乙把b看成了什么(2)求出原方程组的正确解.二元一次方程姐解法练习题稱选券孝签箋与试题解析-・解答題(共16小题) 「求适合冒竽恥X,沖值.X_15点评：本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法.考点：解二元一次方程组.分析：(1) (2)用代入消元法或加减消元法均可；(3) (4)应先去分母、去括号化简方程组，再进一步釆用适宜的方法求解. 解答：解：(1)①-②得，-x=-2,解得x=2,把x=2代入①得，2+y=1, 解得y=-1.考点: 分析:解二元一次方程组. 先把两方程变形(去分母)，得到一组新的方程!$ — 0^0y，然后在用加减消元法消去未知数6x+y=3解答:求出y 的值，继而求出x 的值.•2^1 ⑴ 牛⑵»由(1) X2 得：3x - 2y=2 (3), 由(2) X3得：6x+y=3 (4), (3) X2 得：6x -4y=4 (5), (5) - (4)得：y=-l,5把y 的值代入(3)得：x 起，15X,解：由题意得：2.解下列方程组(1)严尸1 (2)严7尸-5 k 2x+y=3[3x+2y=12rx v 4(3)刁気3 (x-4) =4 (y+2)⑷芳"1)3x-2 (2y+l) =4故原方程组的解为!x "2尸一 1(2)① X3 ■② X2 彳寻,-13y=-39, 解得，y=3,把y=3代入①得，2x-3X3=-5, 解得x=2・ 故原方程组的解为!x=2.1尸3考解二元一次方程纽.(3)原方程组可化为?3x+4y=16 3x- 4y=20①+②得，6x=36,x=6,①-②得.8y=-4,4-所以原方程组的解为x=61-2(4)原方程组可化为：- 6x+2y=- 9 3x -①x 2+②得，x=i,3把x 二代入②得,3xi-4y=6,33所以原方程组的解为彳点评：利用消元法解方程组，要根据未知数的系数特点选择代入法还是加减法:① 相同未知数的系数相同或互为相反数时，宜用加减法: ② 其中一个未知数的系数为1时，宜用代入法.3 •解方程组:专计算题.分先化简方程组，再进一步根据方程组的特点选用相应的方法：用加减法.析■解f4x-3y=12 ①答解：原方程组可化为—,[3x-4y=2 ②■①X4-②X3,得7x=42,解得x=6・把x=6代入①，得y=4.所以方程组的解为f X=6.（y=4占・八・0 ■评二元一次方程纽无论多复杂，解二元一次方程组的基本思想都是消元•消元的方法有代入法和加减法.4. 解方程纽:考点：解二元一次方程组.专题：计算题.分析：把原方程组化简后，观察形式.选用合适的解法，此题用加减法求解比较简单.解答：,f2x+3y=13 ①解：（1）原方程组化为q 心]弧-3尸5②①+②得：6x=18,Ax=3.代入①得：y=X3” x=3所以原方程组的解为7・点评：要注意：两个二元一次方程中同一未知数的系数相反或相等吋，把这两个方程的两边相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法.本题适合用此法.①-②得：2=4k, 所以k —,25.解方程纽:(s- t) - 2 (s+t) =10 |_3 (s-t) +2 (s+t) =26考点：解二元一次方程组. 专题：计算题；换元法.分析：本题用加减消元法即可或运用换元法求解.3 (s - t) - 2 (s+t) =10 ① 3 (s-t) +2 (s+t) =26 ②’①-②，得s+t=4,①+②，得s-t=6t n fs+t=4 即 广,[s- t=6s=5解得q[■t 二-1 所以方程组的解为J s=5・[t 二-1点评：此题较简单，要熟练解方程组的基本方法：代入消元法和加减消元法.(y —3Y ——6.已知关于x, y 的二元一次方程y 二kx+b 的解有( 和彳1尸4 I 尸2(1) 求k, b 的值. (2) 当x=2时.y 的值. (3)当x 为何值吋，y=3考点：解二元一次方程组. 专题：计算题.分析：(1)将两组x, y 的值代入方程得出关于k 、b 的二元一次方程组4=3k+b 2= - k+b法求出k 、b 的值.,再运用加减消元解答:(2) 将(1)中的k 、b 代入，再把x=2代入化简即可得出y 的值. (3)将(1)中的k 、b 和y=3代入方程化简即可得出x 的值.解：#3k+b …① 2二一 k+b …②依题意得：所以哼(2)把y 二3代入，得x=1・点评：本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的代入，可得出要求的 数.7.解方程组：x - 2y=3(1) X _7 ;3考点：解二元一次方程组.分析：根据各方程组的特点选用相应的方法：(1)先去分母再用加减法，(2)先去括号，再转化为整式方程解答.解答：fx-2y=3解：(1)原方程组可化为，2x - 5y=7①X2-②得：y= - 1,< y= - 1代入①得: x=1・⑵原方程可化为严仏7曲Jlx+4x+8y=45X- 4y=3 15x+8y=45①x 2+②得:3x - 2 llx+4 (x+2y)二3 (x+2y)二45•••方程组的解为Q1尸_17x=51, x =3,将x=3代入x-4y 二3中得：y 二0.•••方程组的解为J X=3.ly=o点评：这类题目的解题关键是理解解方程纽的基本思想是消元，掌握消元的方法有：加减消元法和代 入消元法.根据未知数系数的特点，选择合适的方法.—+~二 18•解方程纽：3 53 (x+y) +2 (x-3y) =15考点：解二元一次方程组. 专题：计算题.分析：本题应把方程组化简后，观察方程的形式，选用合适的方法求解.①+②，得10x=30,x=3,代入①，得15+3y=15,y 二0・ 则原方程组的解为］X=：3.1尸0点评：解答此题应根据以方程纽的特点，有括号的去括号，有分母的去分母，然后再用代入法或加减 消元法解方程组.x+4y=149.解方程组：＜ 乂 一3 3[F' 3 "12考点：解二元一次方程组. 专题：计算题.分析：本题为了计算方便，可先把（2）去分母，然后运用加减消元法解本题.两个方程相加，得4x=12, x=3.解答:解：原方程组可化为q石x+3y=15 ①5x-3y=15 ②解答:解: 原方程变形为:x+4y=143x 一 4y= 一 2把x=3代入第一个方程，得4y=11,点评：本题考查的是二元一次方程组的解法，方程中含有分母的要先化去分母，再对方程进行化简、 消元，即可解出此类题目. 10 •解下列方程组：考点：解二元一次方程组.专题：计算题.分析：此题根据观察可知：(1)运用代入法，把①代入②，可得出x, y 的值： (2)先将方程纽化为整系数方程纽，再利用加减消元法求解.由①，得x=4+y ③，代入②,得 4 (4+y) +2y= - 1,③ X2-④X3,得 y 二-24, 把y 二-24代入④，得x=60,解答:把y 二-21代入③，得x=4 -6 6 6*⑵原方程组整理为®+4曲4叟 (2)原方程组整理为 2x+3y=48 ②所以原方程组的解为＜x=60 所以原方程组的解为 y= - 24点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用.11 •解方程纽：=1(1)4 (x+y) -5 (x - y)二2考点：解二元一次方程组.专题：计算题；换元法.分析：方程纽(1)需要先化简，再根据方程组的特点选择解法：方程纽(2)釆用换元法较简单，设x+y 二a, x-y=b,然后解新方程组即可求解. 解答：f4x- 3y=12 解：(D 原方程组可化简为q ,L 3x+2y=12(2)设 x+y=a, x - y=b,匕』二6•:原方程组可化为2 34o —5b 二 2解得(巴lb 二 6x+y=8x- y=l点评：此题考查了学生的计算能力，解题时要细心.12 •解二元一次方程纽:解得彳•:原方程组的解为 x=7v=lX "17⑴9展y=2Q；k3x+4y=10“、［3 (x-1) -4 (丫-4) =0(2) .5 (y-1)二3 35)■考点：解二元一次方程组.专趣：计算题.分析：(1)运用加减消元的方法，可求出x、y的值：(2)先将方程组化简，然后运用加减消元的方法可求出x、y的值. 解答：解：(1)将①X2-②，得15x=30,x=2,把x=2代入第一个方程，得y=・则方程组的解是丿X7；(2)此方程组通过化简可得：\ °尸13- 5尸- 20①-②得：y=7,把y=7代入第一个方程，得x=5・"Y=r则方程组的解是点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过題目的训练达到对知识的强化和运用.ax+5y=10 时，由于粗心，甲看错了方程组中的a,而得解为＜4x 一by= 一4程组中的b,而得解为f x=5.\尸4(1) 甲把a看成了什么.乙把b看成了什么(2) 求出原方程组的正确解.考点：解二元一次方程组.专題：计算题.分析：(1)把甲乙求得方程组的解分别代入原方程组即可：(2)把甲乙所求的解分别代入方程②和①，求出正确的a、b,然后用适当的方法解方程纽. x= - 3,乙看错了方尸一113.在解方程组考点：解二元一次方程组.分析：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可. 解答：解：由原方程组，得3x+2y=22 (1)3x-2y=5 (2)由(1) + (2),并解得 x=^ ⑶，2把(3)代入(1).解得解答:解： (1)把 上二-3 y=- 1代入方程组Q ax+5y=104x 一 by= 一4 把产5代入方程组严5尸10(y=4|^4x- by= - 4 r r5a+20=10<\20-4b=-4，a= _ 2解得：・ lb 二 6甲把a 看成-5;乙把b 看成6;(2) •••正确的a 是-2, b 是&•••方程组为 -2x+5y=104x 一 8y= 一4解得：x=15, y=8.则原方程组的解是J X=15・k y=8点评：此题难度较大，需同学们仔细阅读，弄淸题意再解答. 14.10.2 卩+10.34 4r 9X_2•••原方程组的解初17' r点评：用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去 乘方程的两边，使一个未知数的系数互为相反数或相等； 2. 把两个方程的两边分别相加或相减，消去一个未知数.得到一个一元一次方程： 3 •解这个一元一次方程； 4.将求出的耒知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组 的解.15 •解下列方程组：⑴ x+y=50080%x+60%y=500X 74% ：r 2x+3y=15⑵'x+1 _ 汨4 ■、7 = 5考点：解二元一次方程组.分析：将两个方程先化简，再选择正确的方法进行消元.解答:解:(1)化简整理为严芦00①(4x+3y=1850@®X3,得 3x+3y=500③，②-③，得x=350.把 x=350 代入①，得 350+y 二500,Ay=150.故原方程组的解为f X=35°・ (y=150①X5,得 10x+15y=75③， ② X2,得 10x-14y=46④，③ -④，得29y=29,:.y —1 ・把yh 代入①，得2x+3X1=15, ••x—6.故原方程组的解为!x=6.1 v=l(2)化简整理为Qlx+3y=15 ① 5x - 7y=23@点评：方程纽中的方程不是最简方程的，说好先化成最简方程，再选择合适的方法解方程. 16•解下列方程组：(1) 2x+y=4x+2y=5 考点：解二元一次方程组.分析：观察方程组中各方程的特点，用相应的方法求解.解答：解:(1)①X2-②彳寻：x=1,将xh 代入①得：2+y=4,y=2.•••原方程组的解为!x=1：♦(2)原方程组可化为j x+y=1, ^2x+3y=5①X2 -②得： -y=-3,y =3.将y=3代入①得：x= - 2.点评：解此类題目要注意观察方程组中各方程的特点，釆用加减法或代入法求解. •••原方程组的解为Qx= - 2 y=3 x+y=l20録+30%尸25% X 2。

二元一次方程组解法练习题精选(含答案)————————————————————————————————作者：————————————————————————————————日期：2二元一次方程组解法练习题一．解答题（共16小题） 1．解下列方程组 （1）（2）（3）)(6441125为已知数a a y x a y x ⎩⎨⎧=-=+ （4）（5）（6）．（7）（8）⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x（9）（10） ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2．求适合的x ，y 的值．3．已知关于x ，y 的二元一次方程y=kx+b 的解有和．（1）求k ，b 的值．（2）当x=2时，y 的值． （3）当x 为何值时，y=3？1．解下列方程组（1）（2）；（3）；（4）（5）．（6）（7）（8）（9）（10）；2．在解方程组时，由于粗心，甲看错了方程组中的a ，而得解为，乙看错了方程组中的b ，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解.4二元一次方程组解法练习题精选参考答案与试题解析一．解答题（共16小题）1．求适合的x，y的值．考点：解二元一次方程组．分析：先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法消去未知数x，求出y的值，继而求出x的值．解答：解：由题意得：，由（1）×2得：3x﹣2y=2（3），由（2）×3得：6x+y=3（4），（3）×2得：6x﹣4y=4（5），（5）﹣（4）得：y=﹣，把y的值代入（3）得：x=，∴．点评：本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法．2．解下列方程组（1）（2）（3）（4）．考点：解二元一次方程组．分析：（1）（2）用代入消元法或加减消元法均可；（3）（4）应先去分母、去括号化简方程组，再进一步采用适宜的方法求解．解答：解：（1）①﹣②得，﹣x=﹣2，解得x=2，把x=2代入①得，2+y=1，解得y=﹣1．故原方程组的解为．（2）①×3﹣②×2得，﹣13y=﹣39，解得，y=3，把y=3代入①得，2x﹣3×3=﹣5，解得x=2．故原方程组的解为．（3）原方程组可化为，①+②得，6x=36，x=6，①﹣②得，8y=﹣4，y=﹣．所以原方程组的解为．（4）原方程组可化为：，①×2+②得，x=，把x=代入②得，3×﹣4y=6，y=﹣．所以原方程组的解为．点评：利用消元法解方程组，要根据未知数的系数特点选择代入法还是加减法：①相同未知数的系数相同或互为相反数时，宜用加减法；②其中一个未知数的系数为1时，宜用代入法．3．解方程组：考点：解二元一次方程组．5专题：计算题．分析：先化简方程组，再进一步根据方程组的特点选用相应的方法：用加减法．解答：解：原方程组可化为，①×4﹣②×3，得7x=42，解得x=6．把x=6代入①，得y=4．所以方程组的解为．点评：；二元一次方程组无论多复杂，解二元一次方程组的基本思想都是消元．消元的方法有代入法和加减法．4．解方程组：考点：解二元一次方程组．专题：计算题．分析：把原方程组化简后，观察形式，选用合适的解法，此题用加减法求解比较简单．解答：解：（1）原方程组化为，①+②得：6x=18，∴x=3．代入①得：y=．所以原方程组的解为．点评：要注意：两个二元一次方程中同一未知数的系数相反或相等时，把这两个方程的两边相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法．本题适合用此法．5．解方程组：考点：解二元一次方程组．专题：计算题；换元法．分析：本题用加减消元法即可或运用换元法求解．解答：解：，①﹣②，得s+t=4，①+②，得s﹣t=6，即，解得．所以方程组的解为．点评：此题较简单，要熟练解方程组的基本方法：代入消元法和加减消元法．6．已知关于x，y的二元一次方程y=kx+b 的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？考点：解二元一次方程组．专题：计算题．分析：（1）将两组x，y的值代入方程得出关于k、b 的二元一次方程组，再运用加减消元法求出k、b的值．（2）将（1）中的k、b代入，再把x=2代入化简即可得出y的值．（3）将（1）中的k、b和y=3代入方程化简即可得出x的值．解答：解：（1）依题意得：①﹣②得：2=4k，所以k=，所以b=．（2）由y=x+，把x=2代入，得y=．6（3）由y=x+把y=3代入，得x=1．点评：本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的代入，可得出要求的数．7．解方程组：（1）；（2）．考点：解二元一次方程组．分析：根据各方程组的特点选用相应的方法：（1）先去分母再用加减法，（2）先去括号，再转化为整式方程解答．解答：解：（1）原方程组可化为，①×2﹣②得：y=﹣1，将y=﹣1代入①得：x=1．∴方程组的解为；（2）原方程可化为，即，①×2+②得：17x=51，x=3，将x=3代入x﹣4y=3中得：y=0．∴方程组的解为．点评：这类题目的解题关键是理解解方程组的基本思想是消元，掌握消元的方法有：加减消元法和代入消元法．根据未知数系数的特点，选择合适的方法．8．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题应把方程组化简后，观察方程的形式，选用合适的方法求解．解答：解：原方程组可化为，①+②，得10x=30，x=3，代入①，得15+3y=15，y=0．则原方程组的解为．点评：解答此题应根据各方程组的特点，有括号的去括号，有分母的去分母，然后再用代入法或加减消元法解方程组．9．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题为了计算方便，可先把（2）去分母，然后运用加减消元法解本题．解答：解：原方程变形为：，两个方程相加，得4x=12，x=3．把x=3代入第一个方程，得4y=11，y=．解之得．点评：本题考查的是二元一次方程组的解法，方程中含有分母的要先化去分母，再对方程进行化简、消元，即可解出此类题目．710．解下列方程组：（1）（2）考点：解二元一次方程组．专题：计算题．分析：此题根据观察可知：（1）运用代入法，把①代入②，可得出x，y的值；（2）先将方程组化为整系数方程组，再利用加减消元法求解．解答：解：（1），由①，得x=4+y③，代入②，得4（4+y）+2y=﹣1，所以y=﹣，把y=﹣代入③，得x=4﹣=．所以原方程组的解为．（2）原方程组整理为，③×2﹣④×3，得y=﹣24，把y=﹣24代入④，得x=60，所以原方程组的解为．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．11．解方程组：（1）（2）考点：解二元一次方程组．专题：计算题；换元法．分析：方程组（1）需要先化简，再根据方程组的特点选择解法；方程组（2）采用换元法较简单，设x+y=a，x﹣y=b，然后解新方程组即可求解．解答：解：（1）原方程组可化简为，解得．（2）设x+y=a，x﹣y=b，∴原方程组可化为，解得，∴∴原方程组的解为．点评：此题考查了学生的计算能力，解题时要细心．12．解二元一次方程组：（1）；（2）．考点：解二元一次方程组．8专题：计算题．分析：（1）运用加减消元的方法，可求出x、y的值；（2）先将方程组化简，然后运用加减消元的方法可求出x、y的值．解答：解：（1）将①×2﹣②，得15x=30，x=2，把x=2代入第一个方程，得y=1．则方程组的解是；（2）此方程组通过化简可得：，①﹣②得：y=7，把y=7代入第一个方程，得x=5．则方程组的解是．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．13．在解方程组时，由于粗心，甲看错了方程组中的a ，而得解为，乙看错了方程组中的b ，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．考点：解二元一次方程组．专题：计算题．分析：（1）把甲乙求得方程组的解分别代入原方程组即可；（2）把甲乙所求的解分别代入方程②和①，求出正确的a、b，然后用适当的方法解方程组．解答：解：（1）把代入方程组，得，解得：．把代入方程组，得，解得：．∴甲把a看成﹣5；乙把b看成6；（2）∵正确的a是﹣2，b是8，∴方程组为，解得：x=15，y=8．则原方程组的解是．点评：此题难度较大，需同学们仔细阅读，弄清题意再解答．14．考点：解二元一次方程组．分析：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可．解答：解：由原方程组，得，由（1）+（2），并解得x=（3），把（3）代入（1），解得y=∴原方程组的解为．点评：用加减法解二元一次方程组的一般步骤：1．方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去乘方程的两边，使一个未知数的系数互为相反数或相等；92．把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；3．解这个一元一次方程；4．将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解．15．解下列方程组：（1）；（2）．考点：解二元一次方程组．分析：将两个方程先化简，再选择正确的方法进行消元．解答：解：（1）化简整理为，①×3，得3x+3y=1500③，②﹣③，得x=350．把x=350代入①，得350+y=500，∴y=150．故原方程组的解为．（2）化简整理为，①×5，得10x+15y=75③，②×2，得10x﹣14y=46④，③﹣④，得29y=29，∴y=1．把y=1代入①，得2x+3×1=15，∴x=6．故原方程组的解为．点评：方程组中的方程不是最简方程的，最好先化成最简方程，再选择合适的方法解方程．16．解下列方程组：（1）（2）考点：解二元一次方程组．分析：观察方程组中各方程的特点，用相应的方法求解．解答：解：（1）①×2﹣②得：x=1，将x=1代入①得：2+y=4，y=2．∴原方程组的解为；（2）原方程组可化为，①×2﹣②得：﹣y=﹣3，y=3．将y=3代入①得：x=﹣2．∴原方程组的解为．点评：解此类题目要注意观察方程组中各方程的特点，采用加减法或代入法求解．10。

二元一次方程组练习题计算题1. 解方程组：2x + 3y = 7x - 4y = -6为了求解这个方程组，我们可以使用替代法或消元法。

让我们先尝试使用替代法来求解。

首先，我们可以从第二个等式中解出 x，得到 x = -6 + 4y。

然后，我们将这个表达式代入到第一个等式中，得到：2(-6 + 4y) + 3y = 7化简这个方程，我们得到：-12 + 8y + 3y = 711y = 19y = 19/11现在，我们可以将这个 y 的值代入到第二个等式中，求解 x：x - 4(19/11) = -6x - 76/11 = -6x = -6 + 76/11x = -66/11 + 76/11x = 10/11因此，该方程组的解为 x = 10/11，y = 19/11。

2. 解方程组：3x - 2y = 82x + 5y = -7这次，我们将使用消元法来解方程组。

我们可以通过将第一个等式的两倍加到第二个等式上来消去 x 的系数，得到：3x - 2y = 86x + 10y = -6现在，我们可以将第一个等式的3倍加到第二个等式上来消去 x 的系数，得到：9x - 6y = 246x + 10y = -6接下来，我们将第一个等式的2倍加到第二个等式上来消去 y 的系数，得到：9x - 6y = 2412x + 20y = -12现在，我们得到了两个等式：9x - 6y = 2412x + 20y = -12我们可以通过消去 y 的系数来解这个二元一次方程组。

将第一个等式的 10 倍减去第二个等式的 6 倍，得到：90x - 60y - 72x - 120y = 240 -(-72)18x - 180y = 312化简这个方程，我们得到：18x = 180y + 312x = (180y + 312)/18x = 10y + 52/3现在，我们可以将这个 x 的表达式代入到第一个等式中，得到：9(10y + 52/3) - 6y = 24化简这个方程，我们得到：90y + 468/3 - 6y = 2490y - 18y = 72 - 15672y = -84y = -84/72y = -7/6最后，我们可以将这个 y 的值代入到 x 的表达式中，求解 x：x = 10(-7/6) + 52/3x = -70/6 + 52/3x = -35/3 + 52/3x = 17/3因此，该方程组的解为 x = 17/3，y = -7/6。