最新3受弯构件承载力计算汇总
- 格式:doc
- 大小:602.00 KB
- 文档页数:16

1 、一般构造要求受弯构件正截面承载力计算1 、配筋率对构件破坏特征的影响及适筋受弯构件截面受力的几个阶段受弯构件正截面破坏特征主要由纵向受拉钢筋的配筋率ρ大小确定。
配筋率是指纵受受拉钢筋的截面面积与截面的有效面积之比。
(3-1)式中As——纵向受力钢筋的截面面积,;b——截面的宽度, mm;——截面的有效高度,——受拉钢筋合力作用点到截面受拉边缘的距离。
根据梁纵向钢筋配筋率的不同, 钢筋混凝土梁可分为适筋梁、超筋梁和少筋梁三种类型, 不同类型梁的破坏特征不同。
(1)适筋梁配置适量纵向受力钢筋的梁称为适筋梁。
适筋梁从开始加载到完全破坏, 其应力变化经历了三个阶段, 如图3.8。
第I阶段(弹性工作阶段):荷载很小时,混凝土的压应力及拉应力都很小, 梁截面上各个纤维的应变也很小, 其应力和应变几乎成直线关系, 混凝土应力分布图形接近三角形, 如图3.8(a)。
当弯矩增大时, 混凝土的拉应力、压应力和钢筋的拉应力也随之增大。
由于混凝土抗拉强度较低, 受拉区混凝土开始表现出明显的塑性性质, 应变较应力增加快, 故应力和应变不再是直线关系, 应力分布呈曲线,当弯距增加到开裂弯距时, 受拉边缘纤维的应变达到混凝土的极限拉应变, 此时,截面处于将裂未裂的极限状态, 即第I阶段末, 用Ia表示, 如图3.13(b)所示。
这时受压区塑性变形发展不明显, 其应力图形仍接近三角形。
Ia阶段的应力状态是抗裂验算的依据。
第Ⅱ阶段(带裂缝工作阶段):当弯矩继续增加时, 受拉区混凝土的拉应变超过其极其拉应变,受拉区出现裂缝, 截面即进入第Ⅱ阶段。
裂缝出现后, 在裂缝截面处, 受拉区混凝土大部分退出工作, 未开裂部分混凝土虽可继续承担部分拉力, 但因靠近中和轴很近, 故其作用甚小, 拉力几乎全部由受拉钢筋承担, 在裂缝出现的瞬间, 钢筋应力突然增加很大。
随着弯矩的不断增加, 裂缝逐渐向上扩展, 中和轴逐渐上移。
, 这时截面所能承担的弯矩称为屈服弯矩。




3单筋矩形截面受弯构件正截面承载力计算单筋矩形截面受弯构件是一种常见的结构构件,广泛应用于建筑、桥梁、机械等领域。
它的正截面承载力是指在构件所受到的弯矩作用下,正截面能够承受的最大力矩值。
单筋矩形截面受弯构件的正截面承载力计算一般按照以下步骤进行:1.假设构件正截面处于弹性阶段,根据材料的弹性力学理论,正截面的受弯应力与弯曲弯矩之间的关系为σ=M/W,其中σ为正截面的受弯应力,M为弯矩,W为截面抗弯矩。
2.计算截面抗弯矩W。
对于单筋矩形截面,一般可将其简化为矩形截面,截面抗弯矩W为b*h^2/6,其中b为矩形截面的宽度,h为矩形截面的高度。
3.根据构件的几何尺寸和受力情况,计算弯矩M。
弯矩的计算可以采用静力学方法或者有限元分析方法。
静力学方法一般是通过平衡方程来计算弯矩,有限元分析方法则利用计算机模拟构件的力学行为,得到准确的弯矩数值。
4.将步骤1和步骤2得到的结果代入公式σ=M/W,计算出正截面的受弯应力。
5.根据材料的强度理论或者试验结果,确定构件正截面的抗弯强度。
抗弯强度一般是指正截面可以承受的最大受弯应力。
6.比较步骤4计算出的受弯应力与步骤5确定的抗弯强度,如果受弯应力小于抗弯强度,则正截面具有足够的承载力;如果受弯应力大于抗弯强度,则正截面不能承受所施加的弯矩。
7.如果正截面的承载力不足,可以通过增加构件的尺寸或者采用其他形状的截面来增加其抗弯强度。
需要注意的是,以上的计算步骤是在构件正截面处于弹性阶段的假设下进行的。
如果构件正截面处于塑性阶段或者受到其他复杂的荷载作用,需要进行强度计算,采用不同的计算方法和理论,并考虑构件的完全塑性铰的形成等因素。
总而言之,单筋矩形截面受弯构件正截面承载力的计算是一项重要的结构设计工作,需要根据构件的几何尺寸、材料的性能以及受力情况等因素进行详细的计算分析,确保构件的安全可靠。



受弯构件斜截面承载力计算受弯构件的斜截面承载力计算是结构工程中非常重要的一部分,它涉及到了材料力学和结构力学的知识。
本文将从斜截面的受力情况、受弯构件的内力和应力分析以及承载力计算方法等方面对受弯构件斜截面的承载力进行详细介绍。
首先,我们需要了解受弯构件的受力情况。
受弯构件一般由梁、梁柱等构件组成,通过外力在构件上形成弯曲状态。
在受弯构件中,呈现出不同截面形状的截面受力情况是不同的,其中斜截面的受力最为复杂。
在斜截面上,由于外力的作用,构件上会产生剪力、弯矩和轴力等内力。
我们需要分析内力的分布和大小,以确定构件在弯曲时的受力情况。
对受弯构件的内力和应力分析是计算其承载力的基础。
在计算斜截面的承载力之前,需要通过受力分析确定斜截面上的剪力和弯矩分布。
剪力是指斜截面上所受的垂直于剪断面的作用力,弯矩是指横截面上由于外力产生的弯曲力矩。
这些内力的大小和分布规律决定了构件的受力状态。
通过内力和应力分析,可以计算出斜截面上的正应力和剪应力分布,进而确定构件在所承受的外力下的承载能力。
在进行承载力计算时,常用的方法是根据构件的弯矩和剪力分布确定截面板的受力情况,进而计算截面板的承载能力。
一般情况下,我们利用材料的强度指标来计算截面板的承载能力,例如钢材的强度指标为抗拉强度和屈服强度,混凝土材料常用的强度指标为抗拉强度和抗压强度。
根据不同材料的强度指标,可以确定构件的受弯、受剪和受压的承载能力。
受弯构件斜截面承载力的计算方法有很多,其中一种常用的方法是构造材料的等效矩形截面法。
该方法通过将斜截面分解为矩形和三角形截面两部分,分别计算其受弯和受剪的承载能力,然后将两者的承载能力进行相加,得到整个斜截面的承载能力。
该方法简单易行,并且计算结果较为准确,被广泛应用于工程实际中。
除了等效矩形截面法外,还有一些其他的承载力计算方法,如平衡原则法、应变能方法等。
这些方法也都有其适用的范围和条件,需要根据具体情况加以选择和使用。
1)承载力计算基本资料:已知截面尺寸b 、h 、材料强度f c 、f t 、f y 、钢筋面积A s ,确定需用的计算参数α1、h 0、ξb 。
计算步骤:(1)验算bh A min s ρ≥,满足要求则进入下一步。
此处,%)/4520.0max(y t min f f ,=ρ (2)求受压区高度x ,由s y c 1A f bx f =α得到bf αA f x c 1s y =(3)验算受压区高度x ,此时x 可能出现如下两种情况: 若0b h ξx ≤,则转入(4)—①) 若0b h ξx >,则转入(4)—②) (4)确定受弯承载力M u①由)2(0c 1xh bx f M -≤α,求出受弯受弯承载力M u 。
②求受弯承载力M u 。
取0b h ξx =。
得到)5.01(b b 20c 1u ξξα-=bh f M2) 配筋计算基本资料:已知截面尺寸b 、h 、材料强度f c 、f t 、f y ,确定需用的计算参数α1、h 0、ξb ; 荷载效应M 。
计算步骤:(1) 求受压区高度x ,由)2(0c 1xh bx f M -≤α得到bf Mh h x c 12002--α= (2) 验算受压区高度0b h ξx <,如满足要求则进入下一步. (3) 求受拉钢筋面积A s ,由s y c 1A f bx f =α,得到yc 1s f bxf A α=(4) 验算bh A min s ρ≥,当bh A min s ρ<时取bh A min s ρ=此处%)/4520.0max(y t min f f ,=ρ1)承载力计算基本资料:已知截面尺寸b 、h 、材料强度f c 、f t 、f y 、f ’y 、钢筋面积A ’s 、A s ,确定需用的计算参数α1、h 0、ξb 。
计算步骤:(1)求受压区高度x , 由'y s y c 1-s A f A f bx f ‘=α得b f αA f xc 1s y =(2)验算受压区高度x ,此时x 可能出现如下三种情况:若'2s a x <,则转入①; 若0'≤≤2h x a b s ξ,则转入②若0>h x b ξ,则转入③ (3)确定受弯承载力M u①'2s a x <,由)-('0s s y u a h A f M =求得受弯承载力M u②0'≤≤2h x a b s ξ,由)-()2-('0''01s s y c u a h A f x h bx f M +=α求得受弯承载力M u ③0>h x b ξ,求得受弯承载力M u ,取0h x b ξ=得)-()0.5-1('0''b 201s s y b c u a h A f bh f M +=ξξα2)配筋计算(1)已知M ,求A ’s 、A s基本资料:已知截面尺寸b 、h 、材料强度f c 、f t 、f y ,确定需用的计算参数α1、h 0、ξb ;荷载效应M 。
建筑结构IP课第二讲受弯构件承载力计算(上)3受弯构件承载力计算本讲预备知识:《建筑力学》中的截面平衡方程,M、V的求取。
钢筋和混凝土的力学性能,《混凝土规范》对其应力-应变曲线所做的基本假定。
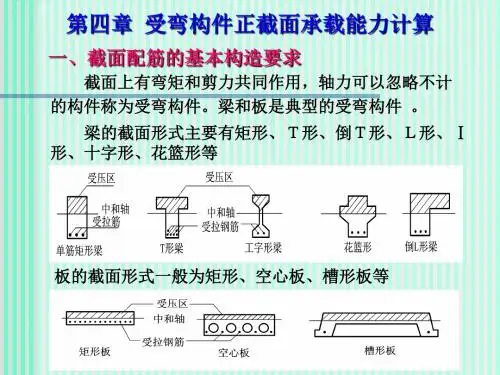
本讲知识结构:1.受弯构件的基本概念2.受弯构件的一般构造要求3.单筋矩形截面梁的三种破坏形式,适筋梁的三个受力阶段4.单筋矩形梁正截面承载力计算的基本假定5.单筋矩形截面梁正截面承载力计算的基本公式和条件6.单筋矩形截面梁的截面设计和截面复核本讲主要内容:受弯构件的两种破坏形式:1.沿弯矩最大截面破坏,称为正截面破坏;2.是沿剪力最大或弯矩和剪力都较大的截面破坏,破坏截面与构件的轴线斜交,称为斜截面破坏。
(a)正截面破坏(b)斜截面破坏图3-1 受弯构件的两种破坏形式3.1一般构造要求3.1.1截面形式在受弯构件中,仅在截面的受拉区配置纵向受力钢筋的截面,称为单筋截面。
同时在截面的受拉区和受压区配置纵向受力钢筋的截面,称为双筋截面。
3.1.2梁的构造要求梁中一般配置纵向受力钢筋、弯起钢筋、箍筋和架立钢筋,如图3-3所示。
图梁的配筋1.截面尺寸梁高与跨度之比lh/称为高跨比。
对于肋形楼盖的主梁为1/8~1/14,次梁为1/12~1/18;独立梁不小于1/15(简支)和1/20(连续)。
矩形截面梁的高宽比bh/.一般取2.5~4.0 (此处h/一般取2.0~3.0;T形截面梁的bb为梁肋宽)。
为便于统一模板尺寸,通常采用矩形截面梁的宽度或T形截面梁的肋宽b= 100、120、150、(180)、200、(220)、250和300mm,300mm以上的级差为50mm,括号中的数值仅用于木模;梁的高度h= 250、300、750、800、900、1000mm等尺寸。
当<h800mm 时,级差为50mm,当≥h800mm时,级差为100mm。
2.混凝土强度等级和保护层厚度梁常用的混凝土强度等级是C25、C30、C35、C40等。
3受弯构件承载力计算1 、一般构造要求受弯构件正截面承载力计算1 、配筋率对构件破坏特征的影响及适筋受弯构件截面受力的几个阶段受弯构件正截面破坏特征主要由纵向受拉钢筋的配筋率ρ大小确定。
配筋率是指纵受受拉钢筋的截面面积与截面的有效面积之比。
(3-1)式中As——纵向受力钢筋的截面面积,;b——截面的宽度,mm;——截面的有效高度,——受拉钢筋合力作用点到截面受拉边缘的距离。
根据梁纵向钢筋配筋率的不同,钢筋混凝土梁可分为适筋梁、超筋梁和少筋梁三种类型,不同类型梁的破坏特征不同。
(1)适筋梁配置适量纵向受力钢筋的梁称为适筋梁。
适筋梁从开始加载到完全破坏,其应力变化经历了三个阶段,如图3.8。
第I阶段(弹性工作阶段):荷载很小时,混凝土的压应力及拉应力都很小,梁截面上各个纤维的应变也很小,其应力和应变几乎成直线关系,混凝土应力分布图形接近三角形,如图3.8(a)。
当弯矩增大时,混凝土的拉应力、压应力和钢筋的拉应力也随之增大。
由于混凝土抗拉强度较低,受拉区混凝土开始表现出明显的塑性性质,应变较应力增加快,故应力和应变不再是直线关系,应力分布呈曲线,当弯距增加到开裂弯距时,受拉边缘纤维的应变达到混凝土的极限拉应变,此时,截面处于将裂未裂的极限状态,即第I阶段末,用Ia表示,如图3.13(b)所示。
这时受压区塑性变形发展不明显,其应力图形仍接近三角形。
Ia阶段的应力状态是抗裂验算的依据。
第Ⅱ阶段(带裂缝工作阶段):当弯矩继续增加时,受拉区混凝土的拉应变超过其极其拉应变,受拉区出现裂缝,截面即进入第Ⅱ阶段。
裂缝出现后,在裂缝截面处,受拉区混凝土大部分退出工作,未开裂部分混凝土虽可继续承担部分拉力,但因靠近中和轴很近,故其作用甚小,拉力几乎全部由受拉钢筋承担,在裂缝出现的瞬间,钢筋应力突然增加很大。
随着弯矩的不断增加,裂缝逐渐向上扩展,中和轴逐渐上移。
由于受压区应变不断增大,受压区混凝土呈现出一定的塑性特征,应力图形呈曲线形,如图3.8?所示。
第Ⅱ阶段的应力状态代表了受弯构件在使用时的应力状态,故本阶段的应力状态作为裂缝宽度和变形验算的依据。
当弯矩继续增加,钢筋应力不断增大,直至达到屈服强度,这时截面所能承担的弯矩称为屈服弯矩。
它标志截面即将进入破坏阶段,即为第Ⅱ阶段极限状态,以Ⅱa表示,如图3.8(d)所示。
第Ⅲ阶段(破坏阶段):弯矩继续增加,截面进入第Ⅲ阶段。
这时受拉钢筋的应力保持屈服强度不变,钢筋的应变迅速增大,促使受拉区混凝土的裂缝迅速向上扩展,中和轴继续上移,受压区混凝土高度缩小,混凝土压应力迅速增大,受压区混凝土的塑性特征表现得更加充分,压应力呈显著曲线分布[图3.8(e)]。
到本阶段末(即Ⅲa阶段),受压边缘混凝土压应变达到极限应变,受压区混凝土产生近乎水平的裂缝,混凝土被压碎,甚至崩脱[图3.8(a)],截面宣告破坏,此时截面所承担的弯矩即为破坏弯矩Mu,这时的应力状态作为构件承载力计算的依据[图3.8(f)]。
图适筋梁工作的三个阶段由上述可知,适筋梁的破坏始于受拉钢筋屈服,从受拉钢筋屈服到受压区混凝土被压碎(即弯矩由增大到),需要经历较长过程。
由于钢筋屈服后产生很大塑性变形,使裂缝急剧开展和挠度急剧增大,给人以明显的破坏预兆,这种破坏称为延性破坏。
适筋梁的材料强度能得到充分发挥。
见图3-9a(2)超筋梁纵向受力钢筋配筋率大于最大配筋率的梁称为超筋梁。
这种梁由于纵向钢筋配置过多,受压区混凝土在钢筋屈服前即达到极限压应变被压碎而破坏。
破坏时钢筋的应力还未达到屈服强度,因而裂缝宽度均较小,且形不成一根开展宽度较大的主裂缝[图3.9(b)],梁的挠度也较小。
这种单纯因混凝土被压碎而引起的破坏,发生得非常突然,没有明显的预兆,属于脆性破坏。
实际工程中不应采用超筋梁。
(3)少筋梁配筋率小于最小配筋率的梁称为少筋梁。
这种梁破坏时,裂缝往往集中出现一条,不但开展宽度大,而且沿梁高延伸较高。
一旦出现裂缝,钢筋的应力就会迅速增大并超过屈服强度而进入强化阶段,甚至被拉断。
在此过程中,裂缝迅速开展,构件严重向下挠曲,最后因裂缝过宽,变形过大而丧失承载力,甚至被折断[图3.9(c)]。
这种破坏也是突然的,没有明显预兆,属于脆性破坏。
实际工程中不应采用少筋梁。
2 、单筋矩形截面梁受弯构件正截面承载力计算根据换算后的等效矩形应力图形,利用静力平衡条件,可得到单筋矩形构件正截面抗弯承载力的两个基本公式。
1. 两个基本公式板的截面有效高度。
图3-13 梁板有效高度的确定方法2. 两个条件:1)为了避免出现少筋情况,必须控制截面配筋率,即最小配筋率。
对于受弯构件,2) 为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度小于界限相对受压区高度,即,或3. 计算例题[例]某钢筋混凝土矩形截面梁,截面尺寸b×h=200mm×500mm,混凝土强度等级C25,钢筋采用HRB400级,纵向受拉钢筋3φ18,混凝土保护层厚度25mm。
该梁承受最大弯矩设计值M =100kN·m。
试复核梁是否安全。
已知条件,[解](1)计算因纵向受拉钢筋布置成一排,故(2)判断梁的条件是否满足要求满足要求。
(3)求截面受弯承载力,并判断该梁是否安全该梁安全。
3 、双筋矩形截面梁受弯构件正截面承载力计算双筋截面受弯构件的破坏特征与单筋截面相似,不同之处是受压区有混凝土和受压钢筋()一起承受压力。
双筋矩形截面受弯构件到达受弯承载力极限状态时的截面应力状态如图3-17。
图双筋矩形截面承载力计算简图基本方程:(3-9)M≤(3-10)公式(3-9)、(3-10)实际上是在单筋矩形截面的公式(3-4)和(3-5)的基础上增加了受压钢筋的作用一项,应注意它是加在混凝土项同一侧,表示帮助混凝土承担部分压力。
适用条件:(1)为了防止超筋梁破坏,应:或(3-11)(2)为了保证受压钢筋能达到规定的抗压强度设计值,应(3-12)在实际设计中,若出现< 的情况,则说明此时受压钢筋所受到的压力太小,压应力达不到抗压设计强度,这样公式(3-9)和(3-10)中的只能用??代人,由于是未知数,使得计算非常复杂,故《混凝土规范》建议在时,近似取,即假定受压钢筋合力点受压混凝合力点相重合,这样处理对截面来说是偏于完全的。
对取矩,得:4 、T形正截面承载力计算在矩形截面受弯构件的承载力计算中,是不考虑混凝土的抗拉强度的,因此,如果将受拉区两侧混凝土挖去,形成如图所示的T形截面,可以降低结构自重,节约材料,获得经济效果。
图 T形截面1、翼缘计算宽度试验表明,T形梁破坏时,其翼缘上混凝土的压应力是不均匀的,越接近肋部应力越大,超过一定距离时压应力几乎为零。
在计算中,为简便起见,假定只在翼缘一定宽度范围内受有压应力,且均匀分布,该范围以外的部分不起作用,这个宽度称为翼缘计算宽度,用表示,其值取表3-3中各项的最小值。
表T形、I形及倒L形截面受弯构件翼缘计算宽度项次考虑情况T形截面、I形截面倒L形截面肋形梁、肋形板独立梁肋形梁、肋形板1 按计算跨度考虑2 按梁(纵肋)净距考虑-3按翼缘高度考虑--b2、T形截面分类按T形截面受弯构件按受压区的高度不同,分为第一类和第二类T形截面:第一类T形截面,中和轴在翼缘内,即;第二类T形截面,中和轴在梁肋内,即。
3、两类T形截面的计算公式1)第一类T形截面承载力在计算截面的正载面承载力时,不考虑受拉区混凝土参加受力。
因此,第一类T形截面(图3-21)相当于宽度的矩形截面,可用代替b按矩形截面的公式计算图第一类T形截面的计算简图两个基本公式适用条件或其中,式(3-18)一般均能满足,可不必验算。
2)第二类T形截面承载力基本公式::适用条件其中式(3-23)条件一般均能满足,往往不必验算。
两种T形截面的判别图判别T形截面类别的计算简图两类T形截面的判别:当中和轴通过翼缘底面,即时为两类T形截面的界限情况。
由平衡条件显然,若≤或M ≤则,即属于第一类T形截面。
若或则,即属于第二类T形截面。
4、简化公式计算法(利用表格进行计算):在进行截面计算时,为简化计算,也可利用现成的表格。
公式(3-4)可改写成 ( a )公式(3-5a)可改写成 ( b )式中 ( c )( d )利用式(c),(d)就可制成受弯构件正截面强度计算表格。
受弯构件斜截面承载力计算梁的斜截面承载力包括斜截面受剪承载力和斜截面受弯承载力。
在实际工程设计中,斜截面受剪承载力通过计算配置腹筋来保证,而斜截面受弯承载力则通过构造措施来保证。
1 、受弯构件斜截面受剪破坏形态1、剪跨比λ广义剪跨比λ:计算截面的弯矩M与剪力V和相应截面的有效高度乘积的比值计算剪跨比,为集中荷载作用点至支座的距离,称为剪跨。
在集中荷载作用下,可用计算剪跨比。
2. 配箍率箍筋截面面积与对应的混凝土面积的比值,称为配箍率(见上图)3、斜截面破坏三种形态1)斜压破坏破坏发生条件:多发生在剪力大而弯矩小的区段,即剪跨比λ较小(λ<1)时,或剪跨比适中但腹筋配置过多即配筋率较大时,以及腹板宽度较窄的T形或I形截面。
破坏特征:发生斜压破坏的过程首先是在梁腹部出现若干条平行的斜裂缝,随着荷载的增加,梁腹部被这些斜裂缝分割成若干个斜向短柱,最后这些斜向短柱由于混凝土达到其抗压强度而破坏(图3-27a)。
这种破坏的承载力主要取决于混凝土强度及截面尺寸,而破坏时箍筋的应力往往达不到屈服强度,钢筋的强度不能充分发挥,且破坏属于脆性破坏,故在设计中应避免。
防止破坏发生的措施:为了防止出现这种破坏,要求梁的截面尺寸不得太小,箍筋不宜过多。
图3-27 梁斜截面破坏形态2)斜拉破坏破坏发生条件:破坏多发生在剪跨比λ较大(λ>3),或腹筋配置过少即配箍率较小时。
破坏特征:发生斜拉破坏的过程是一旦梁腹部出现斜裂缝,很快就形成临界斜裂缝,与其相交的梁腹筋随即屈服,箍筋对斜裂缝开展的限制已不起作用,导致斜裂缝迅速向梁上方受压区延伸,梁将沿斜裂缝裂成两部分而破坏(图3-27c)。
破坏属于脆性破坏。
防止破坏发生的措施:为了防止出现斜拉破坏,要求梁所配置的箍筋数量不能太少,间距不能过大。
3)剪压破坏这种破坏通常发生在剪跨比λ适中(λ=1~3),梁所配置的腹筋(主要是箍筋)适当,即配箍率合适时。
破坏特征:随着荷载的增加,截面出现多条斜裂缝,其中一条延伸长度较大,开展宽度较宽的斜裂缝,称为“临界斜裂缝”。
到破坏时,与临界斜裂缝相交的箍筋首先达到屈服强度。
最后,由于斜裂缝顶端剪压区的混凝土在压应力、剪应力共同作用下达到剪压复合受力时的极限强度而破坏,梁失去承载力(图3-27b)。
梁发生剪压破坏时,混凝土和箍筋的强度均能得到充分发挥,破坏时的脆性性质不如斜压破坏时明显。