典型环节的单位阶跃响应概要

典型环节及其阶跃响应实验报告学院：机械工程学院班级：过控一班姓名：***学号：***********实验内容 比例环节响应 实验人 卢世宝实验时间 教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数响应函数 48.0)(0-==K t U实验波形图实验内容 积分环节模拟电路实验人 卢世宝实验时间 教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数响应函数t t Tt U 740.01)(0-=-=实验波形图48.0)()(21-=-=R RS U S U i o SCS R S U S U i o /740.01)()(0-=-=实验内容 比例积分环节模拟电路实验人 卢世宝实验时间教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数)1(1)()(001010CSR R R CS R CS R S U S U i +-=+-== 0.35+0.014 / S响应函数 t TK t U 1)(0+= = -0.35 – 0.73 t实验波形图实验内容 比例微分环节模拟电路 实验人 卢世宝 实验时间教师签字学号后三位由于本人的学号为416 所以取R=416电路传递函数)11()()(321210+•++-=CS R CS R R R R S U S U i =)122101(+⨯+-S S响应函数)330210210()(CR t e R R R R R R R t U -++-=t e 50088.0088.0(--+-=)实验波形图实验内容 惯性环节模拟电路 实验人 卢世宝实验时间 教师签字学号后三位由于本人的学号为416 所以取 R=416电路传递函数1)()(11+-=CSRRRSUSUi14.0343.0+-=S响应函数)1()(0TteKtU---=)1(343.025te---=实验波形图实验内容PID模拟电路实验人卢世宝实验时间教师签字学号后三位由于本人的学号为416 所以取R=416电路传递函数)1()()(020211001S C R R R S C R R R S Ui S U ++-≈ = - ( 13 + 10S )响应函数]})1(1[1{)(0232211102210021C R te C R C R C R C R t C R R R R t U --++++-=)1(5.1350t e t -+--=实验波形图实验一 典型环节及其阶跃响应一．实验原理和设计合理运用运算放大器本身所具有的基本特性（开环增益高、输入阻抗大、输出阻抗小等）用不同的电阻、电容组成不同的反馈网络来模拟各种典型环节。

实验一: 典型环节与及其阶跃响应一、实验目的1、掌握控制模拟实验的基本原理和一般方法。

2、掌握控制系统时域性能指标的测量方法。

二、实验仪器1、EL-AT-III 型自动控制系统实验箱一台2、计算机一台三、实验原理控制系统模拟实验采用复合网络法来模拟各种典型环节，即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节，然后按照给定系统的结构图将这些模拟环节连接起来，便得到了相应的模拟系统。

再将输入信号加到模拟系统的输入端，并利用计算机等测量仪器，测量系统的输出，便可得到系统的动态响应曲线及性能指标。

若改变系统的参数，还可进一步分析研究参数对系统性能的影响。

四、实验内容构成下述典型一阶系统的模拟电路，并测量其阶跃响应1、比例环节的模拟电路及其传递函数G（S）= −R2/R12、惯性环节的模拟电路及其传递函数G（S）= −K/TS+1K=R2/R1T=R2C3、积分环节的模拟电路及传递函数G（S）=1/TST=RC4、微分环节的模拟电路及传递函数G（S）= −RCS5、比例+微分环节的模拟电路及传递函数G（S）= −K（TS+1）K=R2/R1T=R1C五、实验结果及分析（注：图中黄色为输入曲线、紫色为输出曲线）1、比例环节（1）模拟电路图：（2）响应曲线：2、惯性环节（1）模拟电路图：（2）响应曲线：（3）传递函数计算：实验值：X1=1029ms=1.029s=4TT=0.257sK=Y2/1000=2.017G(S)=-2.017/(0.257S+1) 理论值：G（S）=-2/(0.2S+1)结论：实验值与理论值相近。

3、积分环节（1）模拟电路图：（2）响应曲线：（3）传递函数计算：实验值：5000/(2110/2/2)=9.1G（S）=-9.1/S=-1/0.11S 理论值：G（S）=-1/0.1S结论：实验值与理论值相近。

4、微分环节（1）模拟电路图：（2）响应曲线：5、比例+微分环节（1）模拟电路图：（2）响应曲线：实验二：二阶系统阶跃响应一、实验目的1、研究二阶系统的特征参数，阻尼比ζ和无阻尼自然频率ωn 对系统动态性能的影响。

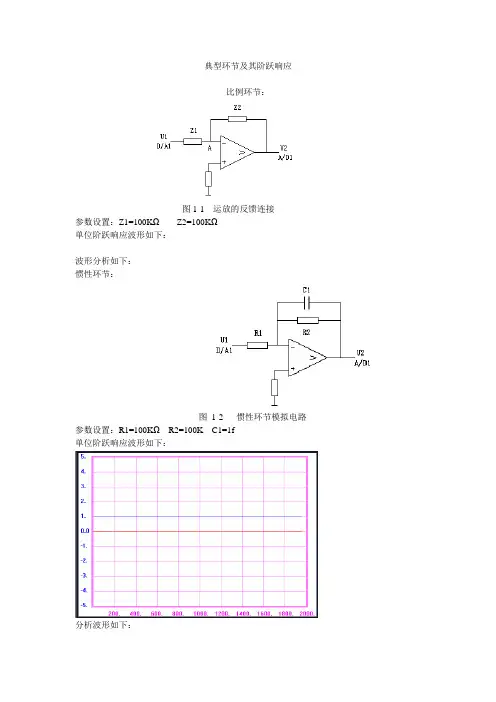
图1-1 运放的反馈连接 典型环节及其阶跃响应
比例环节：
参数设置：Z1=100K Ω Z2=100K Ω 单位阶跃响应波形如下：
波形分析如下： 惯性环节：
图 1-2 惯性环节模拟电路
参数设置：R1=100K Ω R2=100K C1=1f 单位阶跃响应波形如下：
分析波形如下：
积分环节
参数设置：R1=100K C1=1f
单位阶跃响应波形如下：
波形分析如下：
微分环节
微分环节模拟电路参数设置：C1=1f C2=0.01f R2=100K
单位阶跃响应波形如下：
波形分析如下：
比例微分环节
比例微分模拟电路
参数设置：R1=100K R2=100K C1=1f C2=0.01f 单位阶跃波形如下
波形分析如下：
比例积分环节
比例积分环节模拟电路
参数设置：R1=100K R2=200K C1=1f
单位阶跃波形如下
波形分析如下：
比例积分微分环节
比例积分微分模拟电路
参数设置1：R1=100K R2=200K C1=1f C2=0.1f 单位阶跃波形如下
单位阶跃波形如下
波形分析如下：。

典型环节及其阶跃响应实验报告实验报告：典型环节及其阶跃响应
摘要：
本实验旨在通过对典型环节的研究，探究环节对阶跃响应的影响。

通过实验数据的收集和分析，我们成功地建立了模型，并在此基础上进行了进一步探究。

实验操作：
1. 环节参数测量
本实验分别测量了三类环节的参数：惯性环节、比例环节和一阶惯性环节。

在测量期间，我们对示波器进行了正确连接，以确保实验数据的准确性。

2. 阶跃响应测试
我们在实验中使用了脉冲信号作为输入，并记录了系统的阶跃
响应。

3. 数据分析
我们使用MATLAB软件对实验数据进行了分析，并绘制了相
应的图表。

通过对图表的观察，我们可以清晰地看到各个环节对
系统响应的影响。

结果与讨论：
通过对典型环节的实验研究，我们得出了以下结论：
1. 惯性环节会显著影响系统的阶跃响应。

惯性越大，系统的响
应越迟缓，稳态误差也增加。

2. 比例环节是最简单的环节，但是其特性并不适合所有的系统。

在一些情况下，比例环节的加入会加剧系统的振荡。

3. 一阶惯性环节的响应相对较为平滑，且稳态误差也较小。

但是在某些情况下，一阶惯性环节的响应速度可能会比较慢。

结论：
本实验成功研究了典型环节对阶跃响应的影响。

我们成功地建立了模型，并通过对实验数据的分析，得出了较为准确的结论。

我们相信，这些研究成果将会对相关学科的研究和开发产生积极的推动作用。

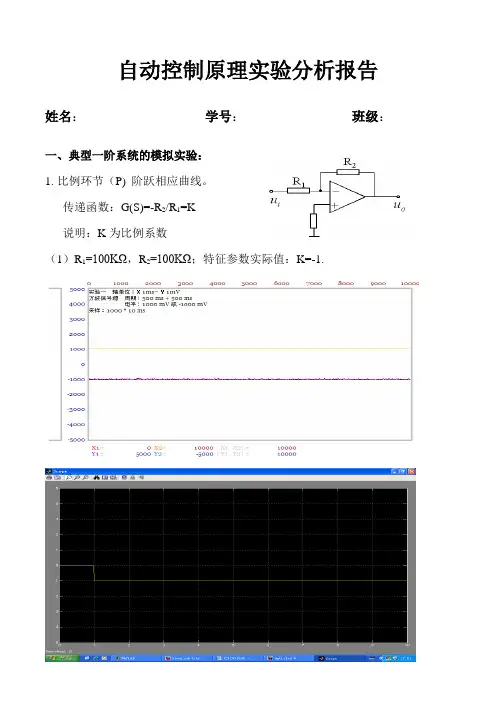
自动控制原理实验分析报告姓名：学号：班级：一、典型一阶系统的模拟实验：1.比例环节（P) 阶跃相应曲线。

传递函数：G(S)=-R2/R1=K说明：K为比例系数（1）R1=100KΩ，R2=100KΩ；特征参数实际值：K=-1.（2）（2）R1=100KΩ，R2=200KΩ；即K=-2.〖分析〗：经软件仿真，比例环节中的输出为常数比例增益K；比例环节的特性参数也为K，表征比例环节的输出量能够无失真、无滞后地按比例复现输入量。

2、惯性环节（T) 阶跃相应曲线及其分析。

传递函数：G(S)=-K/(TS+l) K=R2/R1 , T=R2C说明：特征参数为比例增益K和惯性时间常数T。

（1）、R2=R1=100KΩ , C=1µF；特征参数实际值：K=-1，T=0.1。

（2）、R2=R1=100KΩ , C=0.1µF；特征参数实际值：K=-1，T=0.01。

〖分析〗：惯性环节的阶跃相应是非周期的指数函数，当t=T时，输出量为0.632K，当t=3～4T时，输出量才接近稳态值。

比例增益K表征环节输出的放大能力，惯性时间常数T表征环节惯性的大小，T越大表示惯性越大，延迟的时间越长，反之亦然。

传递函数：G(S)= -l/TS ，T=RC说明：特征参数为积分时间常数T。

（1）、R=100KΩ , C=1µF；特征参数实际值：T=0.1。

（2）R=100KΩ , C=0.1µF；特征参数实际值：T=0.01。

〖分析〗：只要有一个恒定输入量作用于积分环节，其输出量就与时间成正比地无限增加，当t=T时，输出量等于输入信号的幅值大小。

积分时间常数T表征环节积累速率的快慢，T越大表示积分能力越强，反之亦然。

4、比例积分环节（PI) 阶跃相应曲线及其分析。

传递函数：G(S)=K( l+l/TS) K=-R2/R1, T=R2C说明：特征参数为比例增益K和积分时间常数T。

（1）、R2=R1=100KΩ , C=1µF；特征参数实际值：K=-1，T=0.1。

《自动控制》一二阶典型环节阶跃响应实验分析报告一、实验目的本实验旨在通过实际的一二阶典型环节阶跃响应实验，掌握自动控制理论中的基本概念和方法，并能够分析系统的动态响应特性。

二、实验原理1.一阶惯性环节：一阶惯性环节是工程实际中常见的系统模型，其传递函数为G(s)=K/(Ts+1)，其中K为传递函数的增益，T为时间常数。

2.二阶惯性环节：二阶惯性环节是另一类常见的系统模型，其传递函数为G(s)=K/((Ts+1)(αTs+1))，其中K为传递函数的增益，T为时间常数，α为阻尼系数。

3.阶跃响应：阶跃响应是指给定一个单位阶跃输入，观察系统的输出过程。

根据系统的阶数不同，其响应形式也不同。

实验仪器：电动力控制实验台，控制箱，计算机等。

三、实验步骤1.将实验台上的一阶惯性环节模型接入控制箱和计算机，并调整增益和时间常数的初始值。

2.发送一个单位阶跃信号给控制器，观察实验台上的输出响应，并记录时间和输出值。

3.根据记录的数据，绘制一阶惯性环节的阶跃响应图像。

4.类似地，将实验台上的二阶惯性环节模型接入控制箱和计算机，并调整增益、时间常数和阻尼系数的初始值。

5.发送一个单位阶跃信号给控制器，观察实验台上的输出响应，并记录时间和输出值。

6.根据记录的数据，绘制二阶惯性环节的阶跃响应图像。

四、实验结果与分析1.一阶惯性环节的阶跃响应图像如下：（在此插入阶跃响应图像）根据图像可以看出，随着时间的增加，输出逐渐趋于稳定。

根据实验数据，可以计算出一阶惯性环节的增益K和时间常数T的估计值。

2.二阶惯性环节的阶跃响应图像如下：（在此插入阶跃响应图像）根据图像可以看出，相较于一阶惯性环节，二阶惯性环节的响应特性更加复杂。

根据实验数据，可以计算出二阶惯性环节的增益K、时间常数T和阻尼系数α的估计值。

五、实验结论通过本实验，我们成功地进行了一二阶典型环节阶跃响应实验，并获得了实际的响应数据。

通过对实验数据的分析，我们得到了一阶惯性环节和二阶惯性环节的估计参数值。

典型环节及其阶跃响应实验报告哎呀，今天我们聊聊那个“典型环节及其阶跃响应”的实验报告，听起来有点高大上，其实呢，就是看看系统对刺激的反应，咱们就像是在观察一个小宝宝对糖果的反应，立刻就咧嘴笑了，那种欢快的感觉，简直让人心都化了。

你知道的，典型环节就像是一个经典的舞蹈动作，所有的机器、设备，都要围绕着它来转。

我们这次实验就像是给这个舞蹈加点新的花样，看看能不能让它更好看，更精彩。

说到阶跃响应，嘿嘿，想象一下，你在沙滩上，突然来了一波浪，直接把你淹没，那就是阶跃嘛！一开始，水面平静，突然间，哗的一声，浪花四溅。

这个实验就是模拟这种场景，我们用一个信号，给系统一个突如其来的“惊喜”，然后看它的反应。

像小狗听到门铃声那样，瞬间就警觉起来。

我们记录下它的表现，慢慢地分析，像是侦探在拼凑案件一样，越看越有意思。

实验开始的时候，大家都是一副严肃的样子，结果一搞起来，气氛就轻松了很多。

仪器啊，数据啊，真是让人眼花缭乱，搞得我都快晕了。

但没关系，我们的目标明确，简简单单就是想知道这个系统到底是个什么样的“角色”。

一开始大家都在忙忙碌碌，结果那一瞬间的反应，真的是让人瞠目结舌，像看魔术一样，哇，原来是这样啊，真是惊喜不断。

在记录数据的时候，大家开始窃窃私语，笑声不断，有人甚至模仿起了实验设备发出的声音，笑得我差点喷出来。

你看，这个实验不只是冰冷的数字，还有一堆有趣的故事，简直是给我们这个枯燥的学习过程加了不少料。

每当设备显示出一个新的数据点，大家都像中了彩票一样，欢呼雀跃，实验室里瞬间变成了欢乐的海洋。

随着数据的增加，分析起来也变得越来越有趣。

我们开始画图，连接那些数据点，像是在给一个故事编排情节，每一条线都承载着我们的期待。

你可能觉得这有点无聊，其实不然，这过程就像是在拼拼图，一块一块的拼出来，最终看到那个完整的图案，真的是成就感满满。

每当看到图上出现那条漂亮的曲线，大家都像喝了蜂蜜水一样甜。

最终，实验结束，大家都松了一口气，互相道了声辛苦。

六个典型环节的阶跃响应曲线详解1. 引言在信号处理领域中，阶跃响应曲线是描述系统对单位阶跃输入信号的输出响应的一种常用方法。

通过分析阶跃响应曲线，我们可以了解系统的动态特性、稳态误差和稳定性等重要信息。

本文将详细探讨六个典型环节的阶跃响应曲线，以帮助读者更好地理解信号处理中的阶跃响应。

2. 一阶惯性环节让我们来讨论一阶惯性环节的阶跃响应曲线。

一阶惯性环节由一个惯性成分和一个系数组成，其传递函数可以表示为G(s) = k / (τs + 1)，其中k为增益，τ为时间常数。

在阶跃输入信号下，一阶惯性环节的输出响应会经历一个指数衰减的过程。

初始阶段，响应曲线呈现出较大的上升斜率，接近输入信号的增量。

随着时间的推移，响应逐渐趋于稳定的平衡状态。

通过观察阶跃响应曲线的时间常数τ，我们可以推断系统的动态特性以及稳态稳定性。

3. 一阶积分环节接下来，我们将研究一阶积分环节的阶跃响应曲线。

一阶积分环节的传递函数可以表示为G(s) = k / s，其中k为增益。

与一阶惯性环节不同，一阶积分环节的阶跃响应曲线呈现出线性增长的特点。

输出信号随时间的增加而持续积分，并逐渐达到稳态。

在实际应用中，一阶积分环节常用于控制系统中，以改善系统的稳定性和对常数误差的补偿。

4. 一阶滞后环节第三个环节是一阶滞后环节，其传递函数可以表示为G(s) = k / (τs + 1)，其中k为增益，τ为时间常数。

一阶滞后环节的阶跃响应曲线表现出一种惰性的特点。

初始阶段，响应曲线的上升斜率较小，逐渐接近输入信号的增量。

随着时间的推移，响应曲线逐渐逼近稳定的平衡状态。

一阶滞后环节常用于减小系统的动态响应，并提高稳态精度。

5. 二阶过阻尼环节接下来，我们将研究二阶过阻尼环节的阶跃响应曲线。

二阶过阻尼环节的传递函数可以表示为G(s) = k / (τ^2s^2 + 2ζτs + 1)，其中k为增益，τ为时间常数，ζ为阻尼比。

二阶过阻尼环节的阶跃响应曲线表现出较小的震荡和较快的收敛特性。

实验一典型环节及其阶跃响应
概述：
在控制系统中，典型环节是指能够用数学模型描述的一类基本功能模块，包括比例环节、积分环节和微分环节等。

它们在工程中应用十分广泛，可用于控制系统的建模和分析。

本文将介绍比例环节、积分环节和微分环节的定义及其阶跃响应。

一、比例环节
比例环节是指将输入信号按一定比例进行放大或缩小的环节。

用数学式子表示为y=kx，其中k为比例常数，x为输入信号，y为输出信号。

比例环节的作用是调整输入信号与输出信号之间的比例关系。

比例环节的阶跃响应：在阶跃信号的作用下，比例环节的输出将按比例变化。

阶跃信
号是指输入信号在某一时刻瞬间从0跳变到一个确定的值。

对比例环节而言，其阶跃响应
可以表示为：
$$
y(t)=K_{p} u(t)
$$
其中，$K_{p}$为比例放大的增益，$u(t)$为阶跃函数。

二、积分环节
总结：
比例环节、积分环节和微分环节是控制系统中常用的三种典型环节。

它们可以按照不
同的方法进行组合和调整，形成复杂的系统结构，实现对输入信号的更为精细的控制。

在
实际应用中，需要针对具体问题进行具体分析，选择合适的环节组合方案，以实现最佳的
控制效果。

实验一、典型环节及其阶跃响应实验目的1、学习构成典型环节的模拟电路，了解电路参数对环节特性的影响。

2、学习典型环节阶跃响应的测量方法，并学会由阶跃响应曲线计算典型环节的传递函数。

实验内容构成下述典型环节的模拟电路，并测量其阶跃响应。

比例环节的模拟电路及其传递函数示图2-1。

G(S)=-R2/R1惯性环节的模拟电路及其传递函数示图2-2。

G(S)=-K/TS+1 K=R2/R1 ,T=R2*C积分环节的模拟电路及其传递函数示图2-3。

G(S)=1/TS T=RC微分环节的模拟电路及其传递函数示图2-4。

G(S)=-RCS比例加微分环节的模拟电路及其传递函数示图2-5。

G(S)=-K(TS+1) K=R2/R1 T=R2C比例加积分环节的模拟电路及其传递函数示图2-6。

G(S)=K(1+1/TS) K=R2/R1,T=R2C软件使用1、打开实验课题菜单，选中实验课题。

2、在课题参数窗口中，填写相应AD，DA或其它参数。

3、选确认键执行实验操作，选取消键重新设置参数。

实验步骤1、连接被测量典型环节的模拟电路及D/A、A/D连接，检查无误后接通电源。

2、启动应用程序，设置T和N。

参考值：T=0.05秒,N=200。

3、观测计算机屏幕示出的响应曲线及数据记录波形及数据(由实验报告确定)。

实验报告1、画出惯性环节、积分环节、比例加微分环节的模拟电路图，用坐标纸画出所有记录的惯性环节、积分环节、比例加微分环节的响应曲线。

2、由阶跃响应曲线计算出惯性环节、积分环节的传递函数，并与由电路计算的结果相比较。

实验二二阶系统阶跃响应一、实验目的1、研究二阶系统的特征参数，阻尼比ζ和无阻尼自然频ωn 对系统动态性能的影响，定量分析ζ和ωn与最大超调量Mp和调节时间 ts 之间的关系。

2、进一步学习实验仪器的使用方法。

3、学会根据系统阶跃响应曲线确定传递函数。

二、实验原理及电路典型二阶系统的闭环传递函数为其中ζ和ωn对系统的动态品质有决定的影响。

典型环节及其阶跃响应实验报告学院：机械工程学院班级：过控一班姓名：***学号：***********实验内容 比例环节响应 实验人 卢世宝实验时间 教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数响应函数 48.0)(0-==K t U实验波形图实验内容 积分环节模拟电路实验人 卢世宝实验时间 教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数响应函数t t Tt U 740.01)(0-=-=实验波形图48.0)()(21-=-=R RS U S U i o SCS R S U S U i o /740.01)()(0-=-=实验内容 比例积分环节模拟电路实验人 卢世宝实验时间教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数)1(1)()(001010CSR R R CS R CS R S U S U i +-=+-== 0.35+0.014 / S响应函数 t TK t U 1)(0+= = -0.35 – 0.73 t实验波形图实验内容 比例微分环节模拟电路 实验人 卢世宝 实验时间教师签字学号后三位由于本人的学号为416 所以取R=416电路传递函数)11()()(321210+•++-=CS R CS R R R R S U S U i =)122101(+⨯+-S S响应函数)330210210()(CR t e R R R R R R R t U -++-=t e 50088.0088.0(--+-=)实验波形图实验内容 惯性环节模拟电路 实验人 卢世宝实验时间 教师签字学号后三位由于本人的学号为416 所以取 R=416电路传递函数1)()(11+-=CSRRRSUSUi14.0343.0+-=S响应函数)1()(0TteKtU---=)1(343.025te---=实验波形图实验内容PID模拟电路实验人卢世宝实验时间教师签字学号后三位由于本人的学号为416 所以取R=416电路传递函数)1()()(020211001S C R R R S C R R R S Ui S U ++-≈ = - ( 13 + 10S )响应函数]})1(1[1{)(0232211102210021C R te C R C R C R C R t C R R R R t U --++++-=)1(5.1350t e t -+--=实验波形图实验一 典型环节及其阶跃响应一．实验原理和设计合理运用运算放大器本身所具有的基本特性（开环增益高、输入阻抗大、输出阻抗小等）用不同的电阻、电容组成不同的反馈网络来模拟各种典型环节。

计算机模拟系统D/A A/D 输入信号输入信号输出信号输出信号121)(ZZ uu s G -=-=由上式可求得由下列模拟电路组成典型环节的传递函数及其单位阶跃响应。

2．一阶系统时域性能指标s r d t t t ,,的测量方法：的测量方法：利用软件上的游标测量响应曲线上的值，带入公式算出一阶系统时域性能指标。

标。

d t ：响应曲线第一次到达其终值¥y 一半所需的时间。

r t ：响应曲线从终值¥y %10上升到终值¥y %90所需的时间。

所需的时间。

s t ：响应曲线从0到达终值¥y 95%95%所需的时间。

所需的时间。

所需的时间。

3.3.实验线路与原理实验线路与原理实验线路与原理 （注：输入加在反相端，输出信号与输入信号的相位相反） 1．比例环节．比例环节K R R Z Z s G -=-=-=1212)( 比例环节的模拟电路及其响应曲线如图1-31-3。

K ——放大系数。

K 是比例环节的特征量，它表示阶跃输入后，输出与输入的比例关系，可以从响应曲线上求出。

改变1R 或2R 的电阻值便可以改变比例图1-2 运放的反馈连接运放的反馈连接tK -1 0 图1-3 比例环节的模拟电路及其响应曲线比例环节的模拟电路及其响应曲线器的放大倍数K 。

实际物理系统中的比例环节：实际物理系统中的比例环节： Ø 无弹性变形的杠杆；无弹性变形的杠杆； Ø 不计非线性和惯性的电子放大器；不计非线性和惯性的电子放大器； Ø 传递链的速度比；传递链的速度比；Ø 测速发电机的电压与转速的关系。

测速发电机的电压与转速的关系。

2．惯性环节．惯性环节1212121212,11)(C R T R RK Ts KC R R R Z Z s G ==+-=+-=-=惯性环节的模拟电路及其响应曲线如图1-41-4。

式中：K ——静态放大倍数；——静态放大倍数； T ——惯性时间常数；T 和K 是响应曲线的两个特征量。

典型环节及其阶跃响应实验报告典型环节及其阶跃响应实验报告引言：在控制系统中，环节是指系统中的一个组成部分，负责将输入信号转换为输出信号。

环节的特性对于系统的稳定性和性能具有重要影响。

本实验旨在通过对典型环节的阶跃响应进行实验研究，探讨其动态特性和响应行为。

一、比例环节比例环节是控制系统中最简单的环节之一。

它的输出信号与输入信号成比例关系，比例系数称为比例增益。

在实验中，我们选择了一个简单的比例环节进行研究。

实验步骤：1. 搭建比例环节实验装置，将输入信号与输出信号进行连接。

2. 施加一个单位阶跃输入信号。

3. 记录输出信号的变化情况。

实验结果：通过实验，我们观察到比例环节的阶跃响应具有以下特点：1. 输出信号会立即发生变化，但变化幅度与输入信号的大小成比例。

2. 当输入信号从0突变为1时，输出信号也会从0突变为相应的比例值。

3. 比例环节的响应速度较快，但不具备消除稳态误差的能力。

二、积分环节积分环节在控制系统中起到累积误差的作用，能够消除稳态误差。

在实验中，我们研究了积分环节的阶跃响应。

实验步骤：1. 搭建积分环节实验装置，将输入信号与输出信号进行连接。

2. 施加一个单位阶跃输入信号。

3. 记录输出信号的变化情况。

实验结果：通过实验，我们观察到积分环节的阶跃响应具有以下特点：1. 输出信号会随着时间的增加而持续增加，直到达到稳定状态。

2. 当输入信号从0突变为1时，输出信号会持续增加直到稳定。

3. 积分环节的响应速度较慢，但能够消除稳态误差。

三、微分环节微分环节在控制系统中起到抑制过渡过程的作用，能够提高系统的稳定性。

在实验中，我们研究了微分环节的阶跃响应。

实验步骤：1. 搭建微分环节实验装置，将输入信号与输出信号进行连接。

2. 施加一个单位阶跃输入信号。

3. 记录输出信号的变化情况。

实验结果：通过实验，我们观察到微分环节的阶跃响应具有以下特点：1. 输出信号会立即发生变化，但变化幅度与输入信号的变化率成比例。

目录实验一典型环节的阶跃响应测试 1 实验二二阶系统瞬态响应和稳定性测试7 实验三二阶系统的校正装置的设计12 实验四控制系统的频率特性测试15 实验五典型非线性环节的特性18 实验六非线性环节的相平面分析法22 实验七非线性环节的描述函数分析法27 实验八状态变量反馈系统的设计31 实验九温度闭环控制实验34 实验十步进电机调速实验36 实验十一直流电机闭环调速实验38 实验十二随动系统的PID控制41实验一典型环节的阶跃响应测试一. 实验目的要求了解和掌握各典型环节的传递函数及模拟电路图，观察和分析各典型环节的响应曲线。

二．实验设备自动控制原理实验箱、联想计算机、万用表三.实验步骤与内容各典型环节的方块图及传递函数方 块 图实验内容具体参数见表1－11.比例环节比例环节 运放按模拟电路图从左至右依次使用运放单元A1，A4构建,在A1中分别选取R1=100K和R1=200K的反馈阻值2.惯性环节惯性环节 运放依次使用运放单元A4，A2构建，构建R1=200K，只要将A4中IN和OUT之间的第二个短套套上（由下至上），在A4中分别选取电容C=1UF和C=2UF。

3.积分环节积分环节 运放依次使用运放单元A4，A2构建，在A4中分别选取电容C=1UF和C=2UF。

在作该实验时很容易积分饱和，所以有时需要放电.4.比例积分环节比例积分环节 当取C=1UF时运放用A2，A1构建，当取C=2UF时运放用A4，A1构建。

第一运放的反馈由A4的第四个短路套构建（从下至上）。

5.比例微分环节比例微分环节 当R1=10K时运放用A3，A1构建，将A3中IN和OUT 之间的最上面的短路套套好就构成了第一级运放的反馈部分，当R1=20K时利用A1和A3构建，将A1中IN和 OUT 之间的最上面的短路套套好就构成了第一级运放的反馈部分。

6.比例积分微分比例微分积分环节 当R1=10K时 运放依次使用A2，A1构建，第一级放的反馈部分由A2中IN 和OUT之间的第六个短路套构建（由下至上），当R1=20K时 运放依次使用A4，A2构建，第一级运放的反馈部分由A4中IN和OUT之间的最上面的短路套构建1．观测比例、积分、比例积分、比例微分和惯性环节的阶跃响应曲线。

自动控制原理实验报告班级：自动化0906班学生: 伍振希（09213052）张小维（合作）任课教师：苗宇老师目录实验一典型环节及其阶跃响应 (1)一、实验目的 (1)二、实验仪器 (1)三、实验原理 (1)四、实验内容 (1)五、实验步骤 (2)六、实验结果 (3)实验二二阶系统阶跃响应 (6)一、实验目的 (6)二、实验仪器 (6)三、实验原理 (6)四、实验内容 (6)五、实验步骤 (7)六、实验结果 (7)实验三连续系统串联校正 (13)一、实验目的 (13)二、实验仪器 (13)三、实验内容 (13)四、实验步骤 (15)五、实验结果 (15)实验一典型环节及其阶跃响应一、实验目的1. 掌握控制模拟实验的基本原理和一般方法。

2. 掌握控制系统时域性能指标的测量方法。

二、实验仪器1．EL-AT-III型自动控制系统实验箱一台2．计算机一台三、实验原理1．模拟实验的基本原理：控制系统模拟实验采用复合网络法来模拟各种典型环节，即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节，然后按照给定系统的结构图将这些模拟环节连接起来，便得到了相应的模拟系统。

再将输入信号加到模拟系统的输入端，并利用计算机等测量仪器，测量系统的输出，便可得到系统的动态响应曲线及性能指标。

若改变系统的参数，还可进一步分析研究参数对系统性能的影响。

四、实验内容构成下述典型一阶系统的模拟电路，并测量其阶跃响应：1.比例环节的模拟电路及其传递函数如图1-1。

G（S）= R2/R12.惯性环节的模拟电路及其传递函数如图1-2。

G（S）= - K/TS+1K=R2/R1，T=R2C3.积分环节的模拟电路及传递函数如图1-3。

G（S）=1/TST=RC4.微分环节的模拟电路及传递函数如图1-4。

G（S）= - RCS5.比例微分环节的模拟电路及传递函数如图1-5（未标明的C=0.01uf）。

G（S）= -K（TS+1）K=R2/R1，T=R1C五、实验步骤1.启动计算机，在桌面双击图标 [自动控制实验系统] 运行软件。

自动控制原理实验典型环节及其阶跃相应.1 实验目的1. 学习构成典型环节的模拟电路，了解电路参数对环节特性的影响。

2. 学习典型环节阶跃响应的测量方法，并学会由阶跃响应曲线计算典型环节的传递函数。

3. 学习用Multisim 、MATLAB 仿真软件对实验内容中的电路进行仿真。

.2 实验原理典型环节的概念对系统建模、分析和研究很有用，但应强调典型环节的数学模型是对各种物理系统元、部件的机理和特性高度理想化以后的结果，重要的是，在一定条件下， 典型模型的确定能在一定程度上忠实地描述那些元、部件物理过程的本质特征。

1.模拟典型环节是将运算放大器视为满足以下条件的理想放大器：(1) 输入阻抗为∞。

流入运算放大器的电流为零，同时输出阻抗为零；(2) 电压增益为∞：(3) 通频带为∞：(4) 输入与输出之间呈线性特性：2.实际模拟典型环节：(1) 实际运算放大器输出幅值受其电源限制是非线性的，实际运算放大器是有惯性的。

(2) 对比例环节、惯性环节、积分环节、比例积分环节和振荡环节，只要控制了输入量的大小或是输入量施加的时间的长短(对于积分或比例积分环节)，不使其输出工作在工作期间内达到饱和值，则非线性因素对上述环节特性的影响可以避免．但对模拟比例微分环节和微分环节的影响则无法避免，其模拟输出只能达到有限的最高饱和值。

(3) 实际运放有惯性，它对所有模拟惯性环节的暂态响应都有影响，但情况又有较大的不同。

3.各典型环节的模拟电路及传递函数（1） 比例环节的模拟电路如图.1所示，及传递函数为：12)(R R S G -=.1 比例环节的模拟电路2. 惯性环节的模拟电路如图.2所示，及传递函数为： 其中12R R K = T=R 2C图.2 惯性环节的模拟电路3. 积分环节的模拟电路如图.3所示，其传递函数为：111R /1/)(21212212+-=+-=+-=-=TS K CS R R R CS R CSR Z Z S G其中 T=RC.3 积分环节的模拟电路4. 微分环节的模拟电路如图.4所示，及传递函数为：TS S C R S G -=-=11)(其中T=R 1C 11 1/1)(12TSRCS R CS Z Z S G -=-=-=-=.4 微分环节的模拟电路5. 比例＋微分环节的模拟电路如图.5所示，及传递函数为：)1()(+-=TS K S G 其中12R R K = 11C R T =.5 比例＋微分环节的模拟6. 比例+积分环节的模拟电路如图.6所示，及传递函数为：)11()(TS K S G +-= 其中12R R K = C R T 2=.6 比例+积分环节的模拟电路.3 实验内容(1)分别画出比例、惯性、积分、微分、比例＋微分和比例＋积分的模拟电路图。

典型环节的模拟研究及阶跃响应分析实验二典型环节的模拟研究及阶跃响应分析一实验目的1.掌握各典型环节(比例、积分、比例积分、比例微分、惯性环节、比例积分微分环节等)模拟电路的构成方法，培养实验技能。

2.测试并熟悉各典型环节(比例、积分、比例积分、比例微分、惯性环节、比例积分微分环节等)的阶跃响应曲线。

3.了解参数变化对典型环节(比例、积分、比例积分、比例微分、惯性环节、比例积分微分环节等)阶跃响应的影响。

二实验任务与要求1.观测各种典型环节的阶跃响应曲线。

2.观测参数变化对典型环节阶跃响应的影响。

三实验原理本实验是利用运算放大器的基本特性(开环增益高、输入阻抗大、输出阻抗小等)，设置不同的反馈网络来模拟各种环节。

典型环节原理方框图及其模拟电路如下:1、比例环节(P)。

其方框图如图2-1所示:Ui(S)Uo(S)K图1-1A 比例环节方框图图 2-1RRR1010KR10KiUUo--op5op6++10K100K图1-1B 比例环节模拟电路 R0=200K R1=100K;(200K)图 2-2U(S)0其传递函数是: ,K (2-1) Ui(S)比例环节的模拟电路图如图2-2所示，其传递函数是:U(S)R01 (2-2) ,Ui(S)R0比较式(2-1)和(2-2)得 (2-3) K,RR10当输入为单位阶跃信号，即U(t),1(t)时，，则由式(1-1)得到: U(s),1/Sii1 U(S)K,,0S所以输出响应为: (2-4) U,K(t,0)02、积分环节。

其方框图如图2-3所示。

其传递函数为:Ui(S)Uo(S)1TS图 2-3 图1-2A 积分环节方框图RC10KUiRUo--op5op610KR010K100K图1-2B 积分环节模拟电路C=1μf(2μf);R0=200K图 2-4U(S)10 (2-5) ,Ui(S)TS积分环节的模拟电路图如图2-4所示。

积分环节的模拟电路的传递函数为:US()10 (2-6) ,UiSRCS()0比较式(2-5)和(2-6)得:(2-7) T,RC0当输入为单位阶跃信号，即时，，则由式(2-5)得到:U(t),1(t)U(S),1Sii111 ,,,U(S)o2TSSTS所以输出响应为:1 (2-8) Utt(),oT3、比例积分(PI)环节。

实验二 典型环节的单位阶跃响应一、实验目的1、根据对象的单位阶跃响应特性，掌握和深刻理解几种典型环节的特性以及它们特性参数的含义。

2、研究对象传递函数的零极点对系统动态特性的影响。

3、学习Matlab 的基本用法――求取阶跃响应、脉冲响应(step, impulse) ――基本做图方法(hold, plot)二、实验内容 1、比例环节求取K s G )(在不同比例系数K 下的单位阶跃响应，说明比例系数对系统动态过程的影响。

G(s)=K,在不同比例系数K 下的单位阶跃响应Time (sec)A m p l i t u d e由上图可以看出：因为G （s ）=K ，所以被控对象是一个单纯的比例系统。

随着K 的增加，系统的终值是输入信号的K 倍。

2、一阶惯性环节（1）求取1)(+=Ts Ks G 的单位阶跃响应，其中放大倍数K =２，时间常数T =２。

1)(+=Ts Ks G 的单位阶跃响应如下图：0.20.40.60.811.21.41.61.82G(s)=2/(2s+1)的单位阶跃响应Time (sec)A m p l i t u d e（2） 求取122)(+=s s G 的单位脉冲响应，可否用step 命令求取它的脉冲响应？ 122)(+=s s G 的单位脉冲响应如下图：0.10.20.30.40.50.60.70.80.91G(s)=2/(2s+1)的单位m 脉冲响应Time (sec)A m p l i t u d e把传递函数乘以s 再求其单位阶跃响应，就可获得乘s 前的传递函数的脉冲响应。

如下图：0.10.20.30.40.50.60.70.80.91G(s)=2*s/(2s+1)的单位m 阶跃响应Tim e (sec)A m p l i t u d e（3） 围绕给定数值，K 和T 分别取大、中、小三种数值，求取此时对象的单位阶跃响应，说明这两个对象参数对系统过渡过程的动态特性与稳态特性的影响。