高二数学同步讲义(复数的运算)

高二数学课件：《复数的加减法》想要生活的漂亮，需要付出极大忍耐，一不抱怨，二不解释。

【教学目标】（1）把握复数加法与减法运算法则，能熟练地进行加、减法运算；（2）理解并把握复数加法与减法的几何意义，会用平行四边形法则和三角形法则解决一些简单的问题；（3）能初步运用复平面两点间的距离公式解决有关问题；（4）通过学习平行四边形法则和三角形法，培养学生的数形结合的数学思想；（5）通过本节内容的学习，培养学生良好思维品质（思维的严谨性，深刻性，灵活性等）.【教学建议】一、知识结构二、重点、难点分析本节的重点是复数加法法则。

难点是复数加减法的几何意义。

复数加法法则是教材首先规定的法则，它是复数加减法运算的基础，对于这个规定的合理性，在教学过程中要加以重视。

复数加减法的几何意义的难点在于复数加减法转化为向量加减法，以它为根据来解决某些平面图形的问题，学生对这一点不轻易接受。

三、教学建议（1）在复数的加法与减法中，重点是加法.教材首先规定了复数的加法法则.对于这个规定，应通过【教学设计示例】复数的减法及其几何意义【教学目标】1.理解并把握复数减法法则和它的几何意义.2.渗透转化，数形结合等数学思想和方法，提高分析、解决问题能力.3.培养学生良好思维品质（思维的严谨性，深刻性，灵活性等）. 教学重点和难点重点:复数减法法则.难点:对复数减法几何意义理解和应用.【教学过程】（一）引入新课上节课我们学习了复数加法法则及其几何意义，今天我们研究的课题是复数减法及其几何意义.（板书课题:复数减法及其几何意义）（二）复数减法复数减法是加法逆运算，那么复数减法法则为（i）（i）=（）（）i，1.复数减法法则（1）规定:复数减法是加法逆运算；（2）法则:（i）（i）=（）（）i（，，，R）.把（i）（i）看成（i）（1）（i）如何推导这个法则. （i）（i）=（i）（1）（i）=（i）（i）=（）（）i. 推导的想法和依据把减法运算转化为加法运算.推导:设（i）（i）= i（，R）.即复数i为复数i减去复数i 的差.由规定，得（i）（i）= i，依据加法法则，得（）（）i= i，依据复数相等定义，得故（i）（i）=（）（）i.这样推导每一步都有合理依据. 我们得到了复数减法法则，两个复数的差仍是复数.是确定的复数.复数的加（减）法与多项式加（减）法是类似的.就是把复数的实部与实部，虚部与虚部分别相加（减），即（i）（i）=（）（）i.（三）复数减法几何意义我们有了做复数减法的依据复数减法法则，那么复数减法的几何意义是什么?设z= i（，R），z1= i（，R），对应向量分别为，如图由于复数减法是加法的逆运算，设z=（）（）i，所以zz1=z2，z2 z1=z，由复数加法几何意义，以为一条对角线，1为一条边画平行四边形，那么这个平行四边形的另一边2所表示的向量OZ2就与复数zz1的差（）（）i对应，如图.在这个平行四边形中与zz1差对应的向量是只有向量2吗?还有. 因为OZ2 Z1Z，所以向量，也与zz1差对应.向量是以Z1为起点，Z为终点的向量.能概括一下复数减法几何意义是:两个复数的差zz1与连接这两个向量终点并指向被减数的向量对应.（四）应用举例在直角坐标系中标Z1（2，5），连接OZ1，向量1与多数z1对应，标点Z2（3，2），Z2关于x轴对称点Z2（3，2），向量2与复数对应，连接，向量与的差对应（如图）.例2根据复数的几何意义及向量表示，求复平面内两点间的距离公式.解:设复平面内的任意两点Z1，Z2分别表示复数z1，z2，那么Z1Z2就是复数对应的向量，点之间的距离就是向量的模，即复数z2z1的模.假如用d表示点Z1，Z2之间的距离，那么d=|z2z1|. 例3 在复平面内，满足下列复数形式方程的动点Z的轨迹是什么.（1）|z1i|=|z 2 i|；方程左式可以看成|z（1 i）|，是复数Z与复数1 i差的模.几何意义是是动点Z与定点（1，1）间的距离.方程右式也可以写成|z（2i）|，是复数z与复数2i差的模，也就是动点Z与定点（2，1）间距离.这个方程表示的是到两点（1，1），（2，1）距离相等的点的轨迹方程，这个动点轨迹是以点（1，1），（2，1）为端点的线段的垂直平分线.（2）|z i| |zi|=4；方程可以看成|z（i）| |zi|=4，表示的是到两个定点（0，1）和（0，1）距离和等于4的动点轨迹.满足方程的动点轨迹是椭圆.（3）|z 2||z2|=1.这个方程可以写成|z（2）||z2|=1，所以表示到两个定点（2，0），（2，0）距离差等于1的点的轨迹，这个轨迹是双曲线.是双曲线右支.由z1z2几何意义，将z1z2取模得到复平面内两点间距离公式d=|z1z2|，由此得到线段垂直平分线，椭圆、双曲线等复数方程.使有些曲线方程形式变得更为简捷.且反映曲线的本质特征.例4 设动点Z与复数z= i对应，定点P与复数p= i对应.求（1）复平面内圆的方程；解:设定点P为圆心，r为半径，如图由圆的定义，得复平面内圆的方程|zp|=r.（2）复平面内满足不等式|zp|解:复平面内满足不等式|zp|（五）小结我们通过推导得到复数减法法则，并进一步得到了复数减法几何意义，应用复数减法几何意义和复平面内两点间距离公式，可以用复数研究解析几何问题，不等式以及最值问题.（六）布置作业P193习题二十七:2，3，8，9.探究活动复数等式的几何意义复数等式在复平面上表示以为圆心，以1为半径的圆。

高二数学复数的乘方与根式的运算与应用复数是由实数部分与虚数部分组成的数，形如a+bi，其中a为实数部分，b为虚数部分，i为虚数单位。

在高二数学中，我们学习了复数的乘方与根式的运算与应用。

本文将详细介绍这一知识点的相关内容。

一、复数的乘方运算复数的乘方运算是指将一个复数自乘多次的操作。

假设有一个复数z=a+bi，其中a和b均为实数，那么z的乘方可以表示为z^n，其中n为整数。

复数的乘方运算可以通过以下步骤进行：1. 将复数z写成三角形式：z=r(cosθ+isinθ)，其中r为模长，θ为辐角。

2. 对复数的模长和辐角进行乘方运算：r^n为模长的乘方，θn为辐角的乘方。

3. 将结果转换回标准形式，得到复数的乘方。

举个例子来说明。

假设有复数z=2+3i，我们要求z的平方(z^2)。

首先将复数z写成三角形式：r = |z| = √(2^2 + 3^2) = √13θ = arctan(b/a) = arctan(3/2)然后对模长和辐角进行乘方运算：r^2 = (√13)^2 = 13θ^2 = (arctan(3/2))^2最后将结果转换回标准形式：z^2 = 13(cosθ^2+ isinθ^2)二、复数的根式运算复数的根式运算是指求一个复数的n次方根。

假设有一个复数w，我们要求w的n次方根，可以通过以下步骤进行：1. 将复数w写成三角形式：w=r(cosθ+isinθ)，其中r为模长，θ为辐角。

2. 对复数的模长和辐角进行根式运算：r的n次方根为模长，θ/n为辐角。

3. 将结果转换回标准形式，得到复数的n次方根。

举个例子来说明。

假设有复数w=4(cosπ/3+isinπ/3)，我们要求w的立方根。

首先将复数w写成三角形式：r = |w| = 4θ = π/3然后对模长和辐角进行根式运算：r^(1/3) = 4^(1/3)θ/3 = π/9最后将结果转换回标准形式：w^(1/3) = 4^(1/3)(cos(π/9)+isin(π/9))三、复数的应用复数的乘方与根式运算在实际问题中有广泛的应用。

怎样定义复数的加、减、乘运算呢？运算律仍成立吗？
注意到 i2 1，虚数单位 i 可以和实数进行运 算且运算律仍成立，所以复数的加、减、乘运算我 们已经是自然而然地在进行着，只要把这些零散的 操作整理成法则即可了！
1.复数加、减法的运算法则： 已知两复数z1=a+bi, z2=c+di（a,b,c,d是实数） (1)加法法则：z1+z2=(a+c)+(b+d)i;
另外不难证明: z 1 z 2 z 1 z 2,z 1 z 2 z 1 z 2
我们知道,两个向量的和满足平行四边形 法则, 复数可以表示平面上的向量，那么复数 的加法与向量的加法是否具有一致性呢？
设z1=a+bi z2=c+di,则z1+z2=(a+c)+(b+d)i
如图, z1 对应向量 OZ1 , z2 对应向量 OZ2 ,根据向量
(1)2( 2
3i)2 2
01; 3 1 44
例3、 下 列 命 题 中 正 确 的 是 (1)如果 Z1 Z2是实数， Z1、 则Z2互为共轭复数 (2)纯 虚Z数 的 共 轭 复数Z。 是 (3)两 个 纯 虚 数 的 差 虚还 数是 纯 (4)两 个 虚 数 的 差 还 。是 虚 数
可得
x2x24, x23x220.
解得
x3或x2 x3或x6
所以 x3．
课外练习:
1.计算:(1+2 i )2
3 4i
2.计算(i-2)(1-2i)(3+4i) -20+15i 3.计算 (1 i)3 -2+2i 4.若 z C 且 (3 z)i 1 ,则 z -__3_-_i_ . 3

高二数学复数的加减乘除与运算规则复数是数学中的一个重要概念，它由实部和虚部组成，可以表示为a+bi的形式，其中a是实部，b是虚部，i是虚数单位。

在高二数学中，我们学习了复数的加减乘除与运算规则，它们是我们在解决复数相关问题时的基础。

本文将对这些运算规则进行详细的介绍。

一、复数的加法与减法规则复数的加法规则很简单，实部相加得到新的实部，虚部相加得到新的虚部。

例如，给定两个复数z1=a+bi和z2=c+di，它们的和可以表示为(z1+z2) = (a+c) + (b+d)i。

同样地，复数的减法规则也很直观，实部相减得到新的实部，虚部相减得到新的虚部。

例如，给定两个复数z1=a+bi和z2=c+di，它们的差可以表示为(z1-z2) = (a-c) + (b-d)i。

二、复数的乘法规则复数的乘法规则需要我们对两个复数进行分配律的运算。

设有两个复数z1=a+bi和z2=c+di，我们首先计算实部的乘积，然后计算虚部的乘积，最后将两部分相加。

所以，两个复数的乘积可以表示为：(z1*z2) = (a+bi)*(c+di) = (ac-bd) + (ad+bc)i三、复数的除法规则复数的除法规则与乘法规则有些类似，但需要注意的是，我们需要将除数的共轭复数乘以被除数，然后进行分配律的运算。

设有两个复数z1=a+bi和z2=c+di，我们首先计算两个复数的乘积，然后将乘积的实部和虚部除以除数的模的平方。

所以，两个复数的除法可以表示为：(z1/z2) = (a+bi)/(c+di) = [(a+bi)*(c-di)] / [(c+di)*(c-di)]= [(ac+bd) + (bc-ad)i] / (c^2 + d^2)以上就是高二数学中复数的加减乘除与运算规则的详细介绍。

通过掌握这些规则，我们可以更加熟练地进行复数的运算，解决与复数相关的问题。

同时，在实际应用中，我们可以利用这些规则简化计算，并应用到其他数学领域中。

人教A版数学选修1-2 第三章 复 数
设z1 ，z2 为共轭复数，且(z1 ＋z2)2 －3z1z2i＝4－
6i，求z1和z2.
[策略点睛] 解答本题时，也可以利用z的代数形式求解，并注意z的 共轭复数．
人教A版数学选修1-2 第三章 复 数
已知 z∈C， z 为 z 的共轭复数，若 z· －3i z ＝1＋ z 3i，求 z.
复数的乘法运算
z1﹒z2 ＝ (ac－bd)＋(ad＋bc)i .
复数的除法运算
z1 a bi ac bd bc ad 2 2 i (c di 0) 2 2 z 2 c di c d c d
人教A版数学选修1-2 第三章 复 数
如图所示，平行四边形 OABC 的顶点 O，A，C 分 别表示 0,3＋2i，－2＋4i.求：
பைடு நூலகம்
→ (1) AO表示的复数； → (2)对角线CA表示的复数；
(3)对角线OB表示的复数．
→
人教A版数学选修1-2 第三章 复 数
[思路点拨]
人教A版数学选修1-2 第三章 复 数
已知|z1|＝|z2|＝|z1－z2|＝1，求|z1＋z2|.
[思路点拨] 解答本题既可利用z1 ，z2 的代数形式求 解，又可利用复数运算的几何意义求解．
[思路点拨] 解答本题时，也可以利用z的代数形式求
解，并注意z的共轭复数．
人教A版数学选修1-2 第三章 复 数
计算i＋i2＋i3＋…＋i2 013.
[思路点拨] 本题中需求多个in和的值，求解时可考虑
利用等比数列求和公式及in的周期性化简；也可利用in＋in＋1 ＋in＋2＋in＋3＝0(n∈N)化简．
r 叫做复数 z＝a＋bi 的模，记作|z|或|a＋bi|，且|z|＝|a＋bi|＝r ＝

答案
思考2
复数的加法满足交换律和结合律吗？ 答案 满足.
答案
梳理 (1)复数的加、减法法则
设复数z1＝a＋bi，z2＝c＋di(a，b，c，d∈R). ①数学表达式：z1±z2＝(a±c)＋(b±d)i； ②语言叙述：两个复数的和(或差)仍然是一个复数，它的实部是原来两个 复数的实部的和(或差) ，它的虚部是原来两个复数的 虚部 的和(或差). (2)复数加法的运算律 ①交换律：z1＋z2＝ z2＋z1； ②结合律：(z1＋z2)＋z3＝ z1＋(z2＋z3) .
60°，则
z1＋z2
等于
√A.1
B.－1
C.12－
3 2i
D.12＋
3 2i
解析 z1＋z2＝1.
12345
解析 答案
2.设z1＝3－4i，z2＝－2＋3i，则z1－z2在复平面内对应的点位于
A.第一象限
B.第二象限
C.第三象限
D.第四√象限
解析 ∵z1－z2＝5－7i， ∴z1－z2在复平面内对应的点位于第四象限.
∴ x2＋y2＋x＝1， y＝3，
解得xy＝ ＝－ 3，4，
∴z＝－4＋3i.
解析 答案
类型二 复数加、减运算的应用 例2 (1)如图所示，平行四边形OABC的顶点O，A，C分别对应的复数为0， 3＋2i，－2＋4i.求：①A→O表示的复数；②C→A表示的复数；③O→B表示的复数.
解答
(2)已知 z1，z2∈C，|z1|＝|z2|＝1，|z1＋z2|＝ 3，求|z1－z2|.
∴∠AOC＝30°.
同理，得∠BOC＝30°，
∴△OAB 为等边三角形，则|B→A|＝1，B→A对应的复数为 z1－z2，
∴|z1－z2|＝1.

共轭虚数：虚部不为0的共轭复数． 特别地，实数的共轭复数是实数本身．
在复平面内,如果点Z表示复数 z ,点 Z 表
示复数 Z ,那么点Z和 Z 关于实轴对称.
复平面内与一对共轭复数对应的点Z 和 Z
关于实轴对称.
y Z:a+bi
Z:a+bi y
b
b
o
x
-b
-b
ox
Z :a-bi
Z :a-bi
例4 已知复数 x2 x 2 (x2 3x 2)i
记做(a bi) (c di)或 a bi . c di
(a bi) (c di) a bi (a bi)(c di) c di (c di)(c di)
ac
bd (bc c2 d 2
ad )i
ac bd c2 d 2
bc c2
ad d2
i
4、复数的除法法则
那么它们的积
任何 z1 , z2 , z3， C
交换律 z1 z2 z2 z1 结合律 (z1 z2 ) z3 z1 (z2 z3 )
分配律 z1(z2 z3 ) z1z2 z1z3
3、复数的乘方：
对任何 z, z1, z2 C 及 m, n N ，有
zm zn zmn
(4). 2i (1 2i)
复数的四则运算
复数的加法、减法、乘法运算与实数的 运算基本上没有区分，最主要的是在运算中 将i21结合到实际运算过程中去．
1、复数的加法与减法
即:两个复数相加(减)就是实部与实部,虚部与虚部 分别相加(减). 两个复数的和差是一个确定的复数
运算律
探究? 复数的加法满足交换律，结合律吗？
例2.计算 (1 2i)(3 4i)(2 i)

复数的坐标表示1、复平面：根据复数相等的定义，任何一个复数bi a z +=（,a b R ∈），都可以由一个有序实数对(,)a b 唯一确定。

由于有序实数对),(b a 与平面直角坐标系中的点一一对应，因此复数集与平面直角坐标系中的点集之间可以建立一一对应。

这个建立了直角坐标系来表示复数的平面叫做复平面，x 轴叫做 实轴，y 轴叫做虚轴。

实轴上的点都表示实数，除了原点外，虚轴上的点都表示纯虚数，原点对应的复数为000i +=.在复平面内的原点(0,0)表示实数0；实轴上的点(2,0)表示实数2；虚轴上的点(0,1)-表示纯虚数－i ；虚轴上的点(0,5)表示纯虚数5i ；一般的虚数对应的点在四个象限内，如复数23i -对应的点为(2,3)-在第四象限.2、复数与点、向量之间的对应关系： 复数z a bi =+（,a b R ∈）←−−−→一一对应复平面内的点(,)Z a b←−−−→一一对应复平面内的向量OZ3、复数的模(绝对值)与复数z 对应的向量OZ 的模r 叫做复数bi a z +=的模(也叫绝对值)记作z . 由模的定义可知：),0(22R r r b a r bi a z ∈≥+==+=复数和向量进行类比推理：（表中,,,,,a b c d x y R ∈）z z 表示原点(0,0)O 到(,)Z x y 的距离. 12z z -表示复数12,z z 对应的点12,Z Z 之间的距离.例如：4z =表示复数z 对应的点所组成的集合是“以原点为圆心，以4为半径的圆” 类似：(23)4z i -+=表示复数z 对应的点的集合是“以(2,3)为圆心，以4为半径的圆”；12z z i -=+表示复数z 对应的点的集合是“以(1,0)、(0,2)-为端点的线段的中垂线” 【例题讲解】1、（1）复数3z i =-对应的点在第 象限；（2）复数(3)(2)i m i +-+对应的点在第三象限内，则实数m 的取值范围是 （3）设222log (33)log (3)z m m i m =--+-（m R ∈），若z 对应的点在直线210x y -+=上,则m 的值是 .2、（2）“满足2z i z i -++=的复数z 对应的点的轨迹是椭圆”是否正确？（3）已知复数),(R y x yi x z ∈+=，且111zx =的点在复平面上所表示的曲线是（ ）A ．直线B ． 圆C ． 椭圆D ．抛物线3、（1）复数cos sin z i =+θθ（(0,2)θπ∈）在复平面上所对应的点的轨迹是 （2）若（1）中条件改为[0,]θπ∈，则复数z 对应的点的轨迹是4、（1）已知复数12312,1,34z i z i z i =-+=-=-，它们在复平面上所对应的点分别为A 、B 、C ,若(.)O C O A O B R λμλμ=+∈，则λμ+的值是___________.（2）已知复数123,,z z z 满足12121z z z z ==-=，则12z z +=5、（1）已知121,32z i z i =+=-，求12z z -；（2）已知11,12,3z C z i z z ∈=+-=，求z 对应的点Z 的轨迹方程；变题：已知z C ∈，112z i =+，12z z -≤，则z 对应的点Z 的轨迹是 （3）已知12,23,12z C z i z i ∈=+=+且12z z z z -=-，求z 对应的点Z 的轨迹方程6、若z C ∈,且221z i +-=，则22z i --的最小值是变题：已知1,z =求6z i z ++-的最小值及取到最小值时的z【同步精练】1、O 为复平面中坐标原点，O A对应的复数为13i -，将A 点向右平移3个单位，再向上平移1个单位后对应点为B ，则OB对应的复数为2、已知复习11z i =-，235z i =-+分别和复平面上的点,A B 对应，则（1）写出向量AB和BA 对应的复数；（2）求,A B 两点之间的距离.3、复数1212,,z z z z +分别表示点，,,A B C 为原点，且1212z z z z +=-，则四边形O A C B 的形状是__ _；4、在复平面上复数32i --，45i -+，2i +所对应的点分别是A 、B 、C ，则平行四边形A B C D 的对角线B D 所对应的复数是5、已知集合{}P z z i z i =+=-，{}11Q z z =+=，则P Q =6、若复数z 满足4z i z i -++=，则z 在复平面内对应的点Z 的轨迹是7、若复数z 满足221z z +--=，则z 在复平面内对应的点Z 的轨迹是8、若22,z z i z -=-=z =9、已知复数z 满足21z -=，求z 的取值范围.10、已知复数z 满足12z i z i --=++，求z 的取值范围.11、求使12log 434x i i -≥+成立的x 的取值范围.。

-7-
1
2
3
【做一做 3】 若复数 z 同时满足 z-������=2i,������=iz(i 为虚数单位),则 z= . 解析:设 z=a+bi(a,b∈R),则������=a-bi. ∵z-������=2i,∴(a+bi)-(a-bi)=2i, ∴b=1,∴z=a+i,������=a-i. ∵������=iz,∴a-i=(a+i)i. ∴a-i=-1+ai. 由复数相等的充要条件,得 a=-1.∴z=-1+i. 答案:-1+i
1 ������
-5-
1
2
3
【做一做 2】 若复数 z 满足方程 z2+2=0,则 z3 的值为 A.± 2 2 B.-2 2 C.± 2 2i D.-2 2i 解析:设 z=a+bi(a,b∈R),由 z2+2=0, 得 a2-b2+2abi+2=0. ������ = 0, ������2 -������ 2 + 2 = 0, 由 解得 ������ = ± 2, 2������������ = 0, ∴z=± 2i,∴z3=± 2 2i. 答案:C
∴|a+bi|= (-6)2 + (-3)2 =3 5.
答案:C
-3-
1
2
3
2.复数的乘法 (1)复数乘法的定义 设 a+bi 与 c+di 分别是任意两个复数,我们定义复数的乘 法:(a+bi)(c+di)=(ac-bd)+(ad+bc)i.也就是说,两个复数的积仍然是一个复 数.复数的乘法与多项式的乘法是类似的,但在运算过程中,用 i2=-1 进行化 简,然后把实部与虚部分别合并. (2)复数乘法的运算律 复数的乘法满足交换律、结合律以及乘法对加法的分配律.对任何 z1,z2,z3∈C,有 ①z1· z2=z2· z1(交换律); ②(z1· z2)· z3=z1· (z2· z3)(结合律); ③方 对于任意的 z,z1,z2∈C,m,n∈N+,有 ①zm· zn=zm+n; ②(zm)n=zmn; ������ ������ ③(z1· z2)n=������1 ·������2 .

训练题
三 解复数方程
例5［2020·江苏省海头高级中学高二检测］已知复数z＝1+2i（i为虚数单位）. （1）若z·z0＝2z+z0，求复数z0的共轭复数； （2）若z是关于x的方程x2-mx+5＝0的一个虚根，求实数m的值.
训练题
1.已知关于x的方程x2+（1-2i）x+（3m-i）＝0有实数根，求实数m的值.
1.复数的减法法则 （a+bi）-（c+di）＝（a-c）+（b-d）i. 2.两个复数相减，类似于两个多项式相减.
3.两个复数相加（减）就是把实部与实部、虚部与虚部 部分分别相加（减）
4.复数减法的几何意义
两个复数z1＝a+bi，z2＝c+di（a，b，c，d∈R）在复平 面内对应的向量分别是OZ1 ，OZ2 ，那么这两个复数的差z1-z2 对应的向量是OZ1 -OZ2 ，即向量 Z2Z1 .
训练题2［2019·福建厦门高三模拟］已知|z|＝3，且z+3i是纯
虚数，则z＝
.
2.答案： 3i 解析：设z＝x+yi（x，y∈R），∵ x2+y2＝
32，且z+3i＝x+yi+3i＝x+（y+3）i是纯虚数，∴
x 0，
y
3.
∴ z＝3i.
【技巧点拨】 进行复数加、减运算时： （1）复数的实部与实部相加减，虚部与虚部相加减. （2）把i看作一个字母，类比多项式加、减运算中的合并同类项. （3）复数的加法可以推广到多个复数相加的情形. 【注意】 （1）复数z＝a+bi（a，b∈R）对应的点为（a，b）. （2）当已知|z|求解复数z时，一般用待定系数法求解，需设z＝a+bi （a，b∈R）.

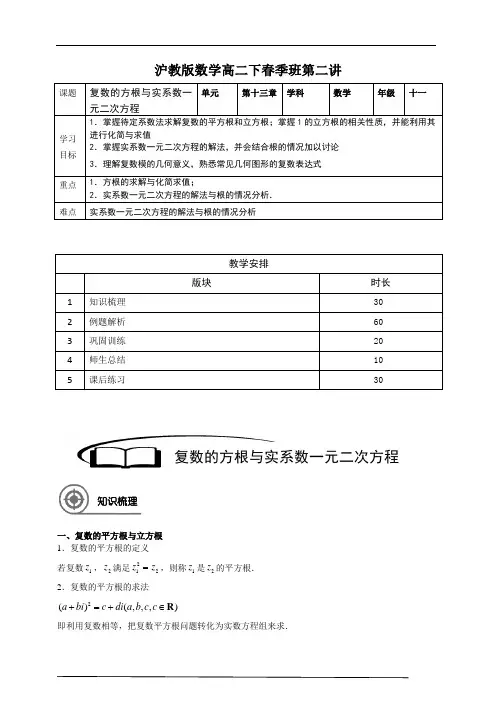
沪教版数学高二下春季班第二讲课题 复数的方根与实系数一元二次方程单元第十三章 学科数学年级十一学习 目标1．掌握待定系数法求解复数的平方根和立方根；掌握1的立方根的相关性质，并能利用其进行化简与求值2．掌握实系数一元二次方程的解法，并会结合根的情况加以讨论3．理解复数模的几何意义，熟悉常见几何图形的复数表达式 重点 1．方根的求解与化简求值；2．实系数一元二次方程的解法与根的情况分析． 难点 实系数一元二次方程的解法与根的情况分析一、复数的平方根与立方根 1．复数的平方根的定义若复数1z ，2z 满足212z z =，则称1z 是2z 的平方根．2．复数的平方根的求法2()(,,,)a bi c di a b c c +=+∈R即利用复数相等，把复数平方根问题转化为实数方程组来求． 教学安排版块 时长1 知识梳理 302 例题解析 603 巩固训练 204 师生总结 10 5课后练习30复数的方根与实系数一元二次方程知识梳理3．复数的平方根的性质复数(0)z z ≠总有两个平方根1z ，2z ，且120z z +=（见图1）． 4．复数的立方根的定义类似的，若复数1z ，2z 满足312z z =，则称1z 是2z 的立方根．5．1的立方根 设复数1322i ω=-+，则21,,ωω都是1的立方根． 6．ω的性质 ①210ωω++=， ②31ω=， ③21322i ωω==--． 可运用这些性质化简相关问题（见图2）． 7．其他有用结论2(1)2i i -=-，2(1)2i i +=二、实系数一元二次方程实系数一元二次方程20(,,,0)ax bx c a b c a ++=∈≠R 中的24b ac ∆=-为根的判别式，那么（1）0∆>⇔方程有两个不相等的实根242b b aca-±-；（2）0∆=⇔方程有两个相等的实根2b a-； （3）0∆<⇔方程有两个共轭虚根242b ac b ia-±-，在（3）的情况下，方程的根与系数关系（韦达定理）仍然成立． 求解复数集上的方程的方法：（1）设(,)z x yi x y =+∈R 化归为实数方程来解决（化归思想）．（2）把z 看成一个未知数（而不是实部和虚部两个未知数），用复数的性质来变形（整体思想）． （3）对二次方程，直接用一元二次方程的求根公式（公式法）． 图1图2三、常见几何图形的复数表达式 复数1z ，2z 为定值，且12z z ≠．（1）线段12Z Z 的中垂线方程：12||||z z z z -=-； （2）以1Z 为圆心，半径为r 的圆方程：1||z z r -=； （3）以1Z 、2Z 为焦点，长轴长为2(0)a a >的椭圆方程：12||||2z z z z a -+-=（其中12||2z z a -<）； （4）以1Z 、2Z 为焦点，实轴长为2(0)a a >的双曲线方程：12||||||2z z z z a ---=（其中12||2z z a ->）．1、复数的平方根与立方根 【例1】求4-及86i -的平方根．【难度】★【答案】4-的平方根为2i 或2i -；86i -的平方根为3i -或3i -+ 【例2】计算：（1）615212(13)(13)112(1)22i i i i i ---⎛⎫-+ ⎪⎝⎭；（2）50820028223(22)112313i i i i i i ⎛⎫-+++-++ ⎪ ⎪ ⎪-+-⎝⎭⎝⎭． 例题解析【注意】 （1）在复数集C 中的一元二次方程的求根公式和韦达定理仍适用，但根的判别式仅 在实数集上有效； （2）实系数一元二次方程在复数集中一定有根，若是虚根则一定成对出现； （3）齐二次实系数二次方程2211220(,,)az bz z cz a b c R ++=∈，将等式两端除以2z 后，将得到一个关于12zz 得实系数一元二次方程；（不作要求） （4）虚系数一元二次方程20(0ax bx c a a b c ++=≠，，，至少有一个为虚数）①判别式判断实根情况失效； ②虚根成对出现的性质失效； 如220x ix --=，虽然70∆=>，但该方程并无实根，不过韦达定理仍适用.【难度】★★【答案】（1）513；（2）247+【例3】记122ω=-+，求1ωω+，221ωω+． 【难度】★★ 【答案】11ωω+=-，2211ωω+=-【例4】已知等比数列123,,,,n z z z z L ，其中11z =，2z x yi =+，3z y xi =+（,,0x y x ∈>R ）． （1）求,x y 的值；（2）试求使1230n z z z z ++++=L 的最小正整数n ；（3）对（2）中的正整数n ，求123n z z z z g g gL g 的值． 【难度】★★【答案】（1）12x y ⎧=⎪⎪⎨⎪=⎪⎩；（2）12n =；（3）1-．【巩固训练】1．复数34i +的平方根是 ．【难度】★ 【答案】(2)i ±+2．计算：（11996= ． （2）151512(1)(1)(1)i -=-+ ． 【难度】★ 【答案】（1）122-；（2）03．已知ω满足等式210ωω++=．（1）计算4(1)ωω++；304050ωωω++；224(1)(1)ωωωω-+-+；（2）求证：对任意复数u ，有恒等式33233(1)()()3(1)u u u u ωω+++++=+； （3）计算：21n n ωω++，*n ∈N ． 【难度】★★【答案】（1）1-；0；4；（2）略；（3）*2**33()1031()032()n n n k k n k k n k k ωω⎧=∈⎪++==-∈⎨⎪=-∈⎩N N N2、复数中的代数式和方程【例5】在复数范围内分解因式：2223x x ++ 【难度】★【答案】222223244x x x x ⎛⎫⎛⎫-+-++=-- ⎪⎪ ⎪⎪⎝⎭⎝⎭2x x ⎛=+- ⎝⎭⎝⎭【例6】复数z 满足方程210z z ++=，求()41z z ++的值 【难度】★★【答案】由210z z ++=得，211022z w z w w w ==-+=∴++=或 所以原式()()4428211w w ww w w w w =++=-+=+=+=-【巩固训练】1．若虚数z 满足327z =，则32315z z z +++的值为 ． 【难度】★★ 【答案】332．1≠ω，13=ω，求32302ωωω+++Λ的值.【难度】★★【答案】122i ω=-+时，原式=15-；122ω=--时，原式；3、实系数一元二次方程【例7】已知方程2350()x x m m -+=∈R ，求方程的解．【难度】★【答案】920m ∆=-当0∆>时，即920m <时，32x ±=；当0∆=时，即920m =时，32x =；当0∆<时，即920m >时，32i x ±=．【例8】已知βα,是实系数一元二次方程02=++c bx ax 的两个虚根，且2αβ∈R ，求βα的值．【难度】★★【答案】∵2αβ∈R ，∴2222ααβαββαβ=⇒=，即330αβ-=∴12αβ=-± 【例9】已知12,x x 是实系数方程20x x p ++=的两个根，且满足12||3x x -=，求实数p 的值． 【难度】★★ 【答案】14p ∆=-，（1）当0∆≥时，即14p ≤时，12,x x 是实根，∴12||3x x -==，即32p =⇒=-；（2）当0∆<时，即14p >时，12,x x 是共轭虚根，设1(,)x a bi a b =+∈R ，则2x a bi =-， ∴123|||2|2||32x x bi b b -===⇒=±，由1221x x a +==-，得12a =-．从而21215||2p x x x ===．综上，2p =-或52．【例10】已知,αβ是实系数一元二次方程230x mx -+=的两个根，求||||αβ+的值．【难度】★★【答案】212m ∆=-，（1）当0∆≥时，即m ≥m ≤-30αβ=>，∴||||||||m αβαβ+=+=；（2）当0∆<时，即m -<<||||2||αβα+===【例11】已知复数12,z z 满足1||2z =，2||1z =，12||2z z -=，求12z z ． 【难度】★★【答案】212121211121222||()()4z z z z z z z z z z z z z z -=--=⋅-⋅-⋅+⋅=， ∴12121z z z z ⋅+⋅=， ∴122211211z zz z z z z z ⋅⋅+⋅⋅=， ∴122141z zz z +=． 令12z t z =，则141t t+=， ∴240t t -+=，∴122t i =±，即1212z z =．【例12】（1）方程20()x px k p -+=∈R 有一个根为12i +，求实数k 的值； （2）方程240x x k -+=有一个根为12i +，求k 的值． 【难度】★【答案】（1）由题意：另一个根为12i -，∴(12)(12)5k i i =+-=； （2）由题意2(12)4(12)074i i k k i +-++=⇒=+．【例12】关于x 的方程2(2i)i 0x a b x a b --+-=有实根，且一个根的模是2，求实数a 、b 的值． 【难度】★★【答案】设()t t ∈R 是方程的一实根，则2(2)()i 0t at a bt b -++-=．则220,0t at a bt b ⎧-+=⎨-=⎩．（1）当0b =时，此方程为220x ax a -+=．①有实根，0∆≥即1a ≥或0a ≤． 当根为2时，440a a -+=．得43a =．当根为2-时，440a a ++=．得45a =-． ②有一对共轭虚根即01a <<．模为2，即有4a =（舍）．（2）当0b ≠时，则1t =，此时1a =．又因为模为2，所以b =所以4,30a b ⎧=⎪⎨⎪=⎩或4,50a b ⎧=-⎪⎨⎪=⎩或1,a b =⎧⎪⎨=⎪⎩1,a b =⎧⎪⎨=⎪⎩【巩固训练】1．下列命题在复数集中是否正确？为什么？（1）若,,a b c ∈R ，0a ≠，且240b ac -≥，则方程20ax bx c ++=有两个实数根； （2）若,,a b c ∈R ，0a ≠，且12,x x 是方程20ax bx c ++=的两个根，则12b x x a +=-，12c x x a=； （3）若,,a b c ∈R ，0a ≠，且12,x x 是方程20ax bx c ++=的两个根，则221212||()x x x x -=-；（4）若,,a b c ∈R ，0a ≠，且α是方程20ax bx c ++=的根，则α也是方程的根． 【难度】★★【答案】（1）、（2）、（4）正确，（3）不正确2．若12,x x 为方程270x x -+=的两个根，则212||x x -= ．【难度】★★ 【答案】273．已知,0x y ≠且022=++y xy x ，求20092009()()x y x y x y+++的值. 【难度】★★【答案】14．关于x 的方程222(31)10x m x m --++=的两根为αβ、，且||||3αβ+=，求实数m 的值． 【难度】★★【答案】53m =-或m =5．设αβ、为方程220x x t ++=，（t ∈R ）的两个根，()||||f t αβ=+，（1）求()f t 的解析式；（2）证明关于t 的方程()f t m =，当2m >时恰有两个不等的根，且两根之和为定值． 【难度】★★【答案】（1）0()2,010t f t t t ⎧<⎪=<≤⎨⎪<⎩．．．（2）证明：函数()y f t =的图像关于直线12t =对称（证略） 当(1,)t ∈+∞时，()f t 为增函数，且()(2,)f t ∈+∞； 当(,0)t ∈-∞时，()f t 为减函数，且()(2,)f t ∈+∞．所以当2m >，方程()f t m =在区间(1,)+∞上有唯一解1t ，在区间(,0)-∞上也有唯一解2t ， 则121212t t +=⨯=．4、复数方程综合问题【例13】关于x 的二次方程2120x z x z m +++=中，1z ，2z ，m 都是复数，且21241620z z i -=+，设这个方程的两个根α、β满足||αβ-=||m 的最大值和最小值． 【难度】★★【答案】根据韦达定理有12z z mαβαβ+=-⎧⎨=+⎩∵22212()()444z z m αβαβαβ-=+-=-- ∴2212|()||4(4)|28m z z αβ-=--=．∴2121|(4)|74m z z --=，即|(45)|7m i -+=， 这表明复数m 在以(4,5)C 为圆心，7为半径的圆周上，∴max ||7m =，min ||7m =当5001,150log 22m t m t >⎧⎪<<⎨<-⎪⎩即2log 215050m t -<<．【例14】已知22016220160122016(1)x x a a x a x a x ++=++++g g g ，试求0362016a a a a ++++g g g 的值。

a bi c di
特别地，a+bi=0 a=b=0 .
；宠物X光机 宠物X光机 ；
复数的运算
谓搭配不当；B句“掀起了……”后面缺少了中心词“高潮”，造成动宾搭配不当；C句歧义，“有人认为…… 化有利于”和“有人认为”这种认识“有利于”两个意思间杂，不清楚。 考点：病句判断 点评：本题不难，常见病句容易判断，平时学习中对病句的判断训练比较多，学生具备一 定的能力。把句子写正确是非常重要的，句子通顺才能正确表达意思，传递信息，进行正常的交流。 129．下面这段文字有三句话，各有一处语病，请加以修改。(3分) ①了给百姓创立更为优良的就医环境，卫生部准备在全国推广“先诊疗后结算”的服务模式。②所谓“先诊疗后结算”，是 指患者在门诊诊疗时，先缴纳押金，统一待本次所有诊疗结束后再去结账。③实施“先诊疗后结算”的服务模式，患者就诊时间可节省大约20％以上。 结果①“创立”改为“创设”或“创造”②将“统一”放到“结账”前③删去“以上”，或删去“大约” 解析 130．下面句子没有语病的 一项是（） A．受日本大地震影响，中国部分地区3月16日开始发生食盐抢购。 B．消减贫富差别，建立社会保障体系的关键在于经济能否发展。 C．以快乐心面对人生，于艰难处寻觅快乐，人的生命便有了亮色。 D．通过这个阶段的复习，同学们普遍的成绩提高了。 131．下列文段中有四 处病句，请按提示进行修改：（4分） “开通了腾讯微博，欢迎多交流。”2月25日，继全国人大代表、重庆川剧院院长沈铁梅入驻腾讯微博后，全国人大代表重庆一中校长鲁善坤也开通了腾讯微博。①这样能更广泛的听取关注民意，②与网友“近距离”。③开博不到一周引来上万网民吹捧， ④平均每天增加听众2000余人左右。网友留言纷纷表示支持，大赞校长观念新、意识潮。 ①处语序不当，应将 与 对调 ②处成分残缺，应在句末添加 ③处用词不当，应将 改为 ④处词语赘余，应将 删去 结果①关注与听取②的交流或沟通③吹捧改为追捧④左右或余（4分） 解析 132．下 面这段文字有三句话，各有一处语病，请加以修改。（3分） ①据有关部门报道，我国每年约有近三分之一的城市人口饮水达不到卫生标准。②抓住市场机遇，我市纯净水生产企业发展迅速起来。③为确保纯净水饮用安全，市政府要求纯净水企业努力提高生产。 结果①删去“约”或“近”； ②“发展”与“迅速”换位置③“生产”后面加“质量” 解析 133．下列句子没有语病的一项（ ▲ ）（2分） A．通过收看专题片，使我们认识到人类要与动物和谐相处。 B．2003年10月16日，我们靠自己力量完成了我国首次载人航天飞行，这是中国人永远值得纪念和骄傲的日子。 C．我 们要确保安全生产，防止万无一失。 D．近段时期以来，小王电脑水平有了明显的增强。 结果（2分）B 解析A介词滥用，造成无主语；C语意表达错误，确保万无一失；D搭配不当，水平提高 134．下列各句中没有语病的一项是（）（3分） A．会不会用心观察，能不能重视积累，这是提高 我们写作水平的基本能力。 B．为了防止再出事故，各个单位都加强了“国庆”期间的安全保卫工作。 C．祖国的山山水水使你从来没有如此地鲜明感受到生命的活跃、强盛和存在。 D．刚开学，几个学校的老师找刘小洋同学就如何克服学习困难交换了意见。 结果B（3分） 解析试题分析： A中前后不一致，应删去“会不会”“能不能”；C中不合逻辑，应是“存在活跃和强盛”；D中有歧义。 考点：辨析或修改病句。能力层级为表达运用E。 135．下列句子中没有语病的一项是（）（2分） A．在这次旅游中，许多景点令我一辈子终生难忘。 B．这朴素的话语多么深刻地蕴含着 人生哲理啊！ C．圆明园，其造园之术，可用“因水成景，借景西山”八字来概括。 D．为了避免公路改道不影响市民的日常生活，政府专门召开会议，研究对策，采取措施。 结果C 解析 136．下列句子中没有语病的一项是（2 分） A．中国共产党建党90周年，是中国历史上开天辟地的大 事。 B．能否成功举行校运会，关键是所有部门要全力以赴开展工作。 C．跨进初中的大门，同学们会有许多地方不适应。 D．最近，泰州推行文明服务用语和服务忌语，此举受到广大市民的欢迎。 137．下列句中没有语病的句子是（）（3分） A．为了防止校园安全事故不再发生，各个学 校都加强了安全保卫工作。 B．在创建卫生文明城市的动员会上，各相关部门交换了广泛的意见。 C．我们的教育应该培养学生善于观察、善于思考、善于创造的水平。 D．一本好书可以给你带来许多教益，甚至可以影响你的一生。 结果D 解析 138．下列句子都有语病，在原句上改正过来。 （2分） ①能否推进素质教育是保证青少年健康成长的条件之一。 ②这次会议规定每位发言者的发言时间最多不超过30分钟。 结果①删掉“能否”②删掉“最多”或“不超过”评分：每小题改对得1分。共2分。其他改法正确也可。 解析 139．下列句子没有语病，句意明确的一项是（） （2分） A．毒黄瓜、瘦肉精、塑化剂……种种食品安全问题如雨后春笋般出现在公众面前，令人惴惴不安。 B．环境保护部已全面启动全国辐射环境监测网络，并要求省级环保部门加强预报和监测。 C．在阅读文学名著过程中，常常能够使我们明白许多做人的道理，悟出世间人生的真谛。 D．随着“天宫一号”飞行器的发射升空，中国向空间站时代迈出了坚实的一步。 140．下列句子没有语病的一项是（▲）（2分） A．通过此次班团课，让我懂得了同学之间要互相谦让。 B．他的学习成绩不仅在全校拔尖，而且在班里也名列前茅。 C．在节能环保型社会里，人们的低碳意识 正在进一步增强。 D．具有认真负责的工作态度，是一个人事业成败的关键。 结果C （2分） 解析A介词滥用，造成无主语；B语序不当，递进关系前后颠倒；D一对多，逻辑照应不周，是否具有 141．下面句子没有语病的一项是（）。 （3分） A．夏天的青岛，真是我们纳凉避暑、休闲 的 好季节。 B．我们一定要发扬和继承世界闽商精诚团结、共谋发展的精神。 C．他奋不顾身抢救落水儿童的先进事迹，我们听后非常感动，真是骇人听闻。 D．我们要引导青少年用美的眼光去看世界，用美的心灵去感受世界。 142．下列句子没有语病的一句是（）。（3分） A． 教师公寓发 生重大火灾，为了防止此类事故不再发生，相关部门采取了强有力的应对措施。 B．为打造一个别开生面的亚运会开幕式，在筹备会上，导演们交换了广泛意见。 C．能否帮助孩子树立正确的财富观，是他们形成良好人生观的关键。 D．我们虽然无法控制生命的长度，但是可以拓展生命的宽 度。 结果D 解析 143．下列句子中没有语病的一项是 分) A．我们中学生应学会保护自然，与自然和谐共处。 B．只要打好知识基础，掌握科学思维方法、积极进行创新活动，人人都可成为富有创造力。 C．电脑越来越成为我们这个时代重要的学习和生活上的工具，广泛地提高着我们的生 活。 D．刘文的这篇作文构思新颖，语言流畅，在全校作文比赛中把它评为一等奖。 144．下面是小强写给他爷爷信中的一个片断，加横线的部分有语病，请加以改 正(4分) ……我们已有几个月未见面了，我常常惦念您。①有时思念之初，我恨不得一下子很快到您的身旁，②向您汇报和倾 诉思念之情．爷爷，③通过您多年对我的谆谆教导，使我各方面都有很大进步．目前，我各科成绩都很好，请勿挂念④我打算寒假到您那里去 下面是小强写给他爷爷信中的一个片断，加横线的部分有语病，请加以改 正(4分) ……我们已有几个月未见面了，我常常惦念您。①有时思念之初， 我恨不得一下子很快到您的身旁，②向您汇报和倾诉思念之情．爷爷，③通过您多年对我的谆谆教导，使我各方面都有很大进步．目前，我各科成绩都很好，请勿挂念④我打算寒假到您那里去玩，请您务必同意…… 答：① ② ③ ④ 结果（1）＂一下子＂和＂很快＂删其一 （2）＂汇报＂ 删去 （3）＂通过＂或＂使＂删其一 （4）将＂请您务必同意＂改为＂您同意吗？＂ 解析 145．修改下列画线的病句，每句只改一处。（2分） ① 国际时尚中心前身是坐落位于东外滩杨树浦路、黄浦江之间的百年老厂 第17棉纺织厂，是 市政府为加速时尚产业发展进程、在世博会期间展示 之美和中国之美的标志性工程。经过改建后的 国际时尚中心外墙为清水红砖，②既保留了上世纪20年代老 工业文明的历史年轮，但是融入了当代时尚的审美元素。 - 修改下列画线的病句，每句只改一处。（2分） ① 国际时尚中心前身是坐落位于东外滩杨树浦路、黄浦江之间的百年老厂 第17棉纺织厂，是 市政府为加速时尚产业发展进程、在世博会期间展示 之美和中国之美的标志性工程。经过改建后的 国际时尚中心外墙为清水红砖，②既保留了上世纪20年代老 工业文明的历史年轮，但是融入了当代时尚的审美元素。 146．下列句子中没有语病的一项是（）(2分) A．从 这些小事中，往往反映出一个人的精神境界。 B．姹紫嫣红的月季、芳香四溢的玫瑰，构成了令人陶醉的花的世界。 C．第十个五年计划是我国今后五年发展的总蓝图，是全国人民的努力方向和追求目标。 D．学校采纳并研究了学生会的意见，这是使学生们欢欣鼓舞的事情。 147．下面一段 话中画线句子有两处语病，请找出来加以修改。（4分） 由李少红导演的50集新版《红楼梦》，①经过近3年多时间的筹备、拍摄和后期制作之后，于近日陆续在青岛、四川、 、宁波、温州等地方电视频道进行首轮播出。②从筹拍之初，新版《红楼梦》便经历了一系列风波话题。到如今开播 伊始，它依旧是各方关注的焦点，③在赢得赞誉支持的同时也惹来了无数口角官司。 下面一段话中画线句子有两处语病，请找出来加以修改。（4分） 由李少红导演的50集新版《红楼梦》，①经过近3年多时间的筹备、拍摄和后期制作之后，于近日陆续在青岛、四川、 、宁波、温州等地方 电视频道进行首轮播出。②从筹拍之初，新版《红楼梦》便经历了一系列风波话题。到如今开播伊始，它依旧是各方关注的焦点，③在赢得赞誉支持的同时也惹来了无数口角官司。 第 句，修改： 第 句，修改： 148．下面这段

z1+z2=z2+z1, (z1+z2)+z3=z1+(z2+z3).
例1.计算 (5 6i) (2 i) (3 4i)
解: (5 6 i ) ( 2 i ) (3 4 i )
(5 2 3) ( 6 1 4) i 11i
2.复数的乘法与除法
(1)复数乘法的法则 复数的乘法与多项式的乘法是类似 的,但必须在所得的结果中把i2换成-1, 并且把实部合并.即:
2 (a+bi)(c+di)=ac+bci+adi+bdi
=(ac-bd)+(bc+ad)i.
(2)复数乘法的运算定理
复数的乘法满足交换律、结合律以
及乘法对加法的分配律.
即对任何z1,z2,z3有
a c a bi c di b d
a=b=0
.
特别地，a+bi=0
问题：
a=0是z=a+bi(a、bR)为 纯虚数的
必要不充分条件
注意:一般地,两个复数只能说相等 或不相等,而不能比较大小. 思考:对于任意的两个复数到底能否 比较大小? 答案:当且仅当两个复数都是实数 时,才能比较大小.
1.复数加减法的运算法则：
(1)运算法则:设复数z1=a+bi,z2=c+di, 那么：z1+z2=(a+c)+(b+d)i;
z1-z2=(a-c)+(b-d)i.
即:两个复数相加(减)就是实部与
实部,虚部与虚部分 别相加(减).
(2)复数的加法满足交换律、结合律,
即对任何z1,z2,z3∈C,有

高二数学复数的运算人教实验版〔B 〕[本讲教育信息]一、教学内容：复数的运算二. 学习目标掌握复数的加法，减法，乘法和除法的运算法那么，能运用这些法那么计算相关问题。

三. 考点分析1、复数的加法和减法)R d ,c ,b ,a (i )d b ()c a ()di c ()bi a (∈±+±=+±+。

2、复数的乘法和除法〔1〕复数的乘法按多项式相乘进行，即i )bc ad ()bd ac (bdi bci adi ac )di c )(bi a (2++-=+++=++。

〔2〕复数除法是乘法的逆运算，其实质是分母实数化。

i d c ad bc d c bd ac di c bi a 2222+-+++=++ 注：做复数除法运算时，有如下技巧：i bia i )bi a (i )aib (i )bi a (ai b bi a =++=-+=-+，利用此结论可使一些特殊的计算过程简化。

3、复数的加减运算是按照向量相加减的平行四边形和三角形法那么进行的，见图1、图2。

图1 图24、复数与点的轨迹〔1〕两点间的距离公式：|z z |d 21-=；〔2〕线段的中垂线：|z z ||z z |21-=-；〔3〕圆的方程：r |P z |=-〔以点P 为圆心，r 为半径〕；〔4〕椭圆：a 2|z z ||z z |21=-+-〔2a 为正常数，|z z |a 221->〕；〔5〕双曲线：a 2||z z ||z z ||2l =---〔2a 为正常数，|z z |a 221-<〕。

[典型例题]例1、计算：77i 31i 22i 3i 22⎪⎪⎭⎫ ⎝⎛+--⎪⎪⎭⎫ ⎝⎛-+。

解：原式77)i 3i ()i 1(2i 3)i 1(i 2⎥⎥⎦⎤⎢⎢⎣⎡---⎥⎦⎤⎢⎣⎡-- 7772)i 3i 22(2i 3)i 1(i 2i 3)i 1(i 2-+=⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡--==72)i 3)(i 1(2⎥⎥⎦⎤⎢⎢⎣⎡++ =7732)i 2321()i )(i 1(])i 1[(2+--++ 2i 31i )i 1()i 8(2+-⋅+⋅-= .i )388(388+-+--=例2、1x 1x -=+，求20062006x1x +的值。