固体物理(第5课)晶格振动一维单原子链
- 格式:ppt
- 大小:495.50 KB
- 文档页数:25



一维单原子链晶格振动解析步骤一维单原子链模型是固体物理中的经典模型之一,用于描述晶体中原子的振动行为。
在这个模型中,原子由质量为m的核和劲度系数为K的弹性相互作用构成。
通过对一维单原子链的晶格振动进行分析,可以更好地理解固体中的声子模式和声子色散关系。
下面将介绍一维单原子链晶格振动解析步骤:第一步:建立模型首先,我们要建立一维单原子链的模型。
假设晶格常数为a,原子间距为a/2,一维晶格中的每个原子都沿着x轴定位。
原子间的相互作用由弹簧模型描述,即相邻原子间的相互作用劲度系数为K。
这个模型是一个简单的原子链模型,可以通过它来研究晶格振动的基本性质。
第二步:求解运动方程接下来,我们需要求解原子在这个一维单原子链中的运动方程。
假设第n个原子的位移为Un(t),那么根据牛顿第二定律,可以得出该原子的运动方程为:m*Un’’(t) = -K*(Un(t+0) - 2*Un(t) + Un(t-0))上式中,Un’’(t)表示Un对时间的二阶导数,-K*(Un(t+0) -2*Un(t) + Un(t-0))表示受到的弹性相互作用力。
第三步:假设解的形式由于原子在一维单原子链中的振动属于谐振动问题,我们可以假设原子的位移满足解的形式为:Un(t) = An*exp(i*(k*n*a - ω*t))其中,An是振幅,k是波数,ω是角频率,n是原子的编号。
将这个解代入到运动方程中,可以得到关于角频率ω和波数k的关系式,即声子色散关系。
声子色散关系描述了声子的能量随波数变化的关系,是描述晶体中声子性质的重要工具。
第四步:得到声子色散关系将解的形式代入运动方程,我们可以得到关于角频率ω和波数k的关系式。
具体地,我们可以得到一维单原子链中的声子色散关系为:ω(k) = 2*sqrt(K/m)*|sin(ka/2)|声子色散关系描述了一维单原子链中的声子能量随波数变化的规律。
从这个关系式可以看出,一维单原子链中的声子有声学支和光学支两种振动模式,它们的能量随波数的变化方式不同。

一维原子链的晶格振动方程晶体是由原子或分子组成的周期性排列的结构,其内部的原子或分子通过振动相互作用,从而产生晶格振动。
晶格振动方程描述了一维原子链中原子的振动行为,对研究固体物理和材料科学具有重要意义。
一维原子链的晶格振动方程可以通过简化模型来描述。
我们假设原子链中的原子质量相同,且原子间的相互作用力为弹簧力。
在平衡位置附近,原子的位移可以用小量近似表示,即位移量远小于原子间距。
此时,可以利用胡克定律,将原子间的相互作用力近似为线性弹簧力。
根据胡克定律,弹簧的力与其伸长(或缩短)的长度成正比,且方向与伸长(或缩短)的方向相反。
对于一维原子链中相邻两个原子,其相互作用力可以表示为:F = -k(x - a) - k(x + a)其中,F为相互作用力,k为弹簧常数,x为原子的位移量,a为原子间距。
根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成反比。
在一维原子链中,每个原子的加速度与相邻原子的相互作用力有关,可以表示为:m(d^2x/dt^2) = -k(x - a) - k(x + a)其中,m为原子的质量,d^2x/dt^2为原子的加速度,t为时间。
将上述方程进行简化,可得:d^2x/dt^2 = -k/m * (2x - a - a)化简后得到:d^2x/dt^2 = -2k/m * (x - a/2)这就是一维原子链的晶格振动方程。
从中可以看出,原子的加速度与位移量成正比,且与原子间距和弹簧常数有关。
当原子受到外力作用时,晶格振动方程可以进一步进行修正。
一维原子链的晶格振动方程可以通过求解微分方程得到解析解,也可以通过数值模拟方法进行计算。
对于周期性边界条件下的一维原子链,可以采用傅里叶变换的方法,将晶格振动分解为一系列特定频率的波动模式。
晶格振动在固体物理和材料科学中具有广泛的应用。
通过研究晶格振动,可以揭示物质的热力学性质、电子结构和传热传电等基本行为。
此外,晶格振动还与声学性质、热导率、热膨胀和热容等宏观性质密切相关,对于材料的设计和优化具有重要意义。



第n-2个原子第n-1个原子第n+1个原子第n+2个原子第n个原子maµn-2µn-1µnµn+1µn+2第n-2个原子第n-1个原子第n+1个原子第n+2个原子第n个原子maµn-2µn-1µnµn+1µn+2a一维晶格仅考虑最近邻原子间相互作用时的色散关系qv p ω=2.21∑=qqQ 221∑⎟⎠⎞⎜⎝⎛=•n n m T μ∑••=qiqna q n t Q Nmt ,)e (1)(μ∑∑∑′−′−′=nq qinaq q .q ina q .,t Q t QN T )e ()e (21∑∑∑′+′−′=q nq q ina qq .q .,Nt Q t Q)(e1)()(21∑∑′−′′=q qqq qq t Qt Q,)()(21,..δ∑−=qqqt Qt Q)()(21..∑=qqqt Qt Q)()(21.*.)()(*t Q t Q q q =−动能的正则坐标表示:势能∑−=qinaqq n eQ Nm 1μ∑−−−='')1('11q aq n i q n e QNm μ∑−−=nn n U 21)(21μμβ1(')'(')','1{[1]}()2N ia q q iaq iaq ina q q q q q q n U Q Q e e e emNβ−++==+−−∑∑}2{2∑−−−−=qiaq iaq qq e e Q Q mβ{1cos()}q qqQ Qaq mβ−=−∑代入上式,得:*{1cos()}qqqU Q Q aq mβ=−∑利用)}cos(1{22aq mq −=βω2*12q q q qU Q Q ω=∑2221∑=qq q Q U ω系统势能所以2221∑=qq q Q U ω哈密顿量2221()2q q qqH T U Q Q ω=+=+∑ ——系统复数形式的简正坐标ti q q q eA Nm Q ω=势能动能∑=qq Q T 221 1()[()()]2Q q a q ib q =+)]()([21)(*q ib q a q Q −=∑=qq Q T 2212221∑=qq q Q U ω∑>+=22)]()([21q q b q a T 实数形式的简正坐标令∑>+=222)]()([21q q q b q a U ω能量本征值qq n n qωε=)21(+=2()/exp()()2qq n q q n Q H ξϕωξ=−=本征态函数一个简正坐标对应一个谐振子方程,波函数是以简正坐标为宗量的谐振子波函数。

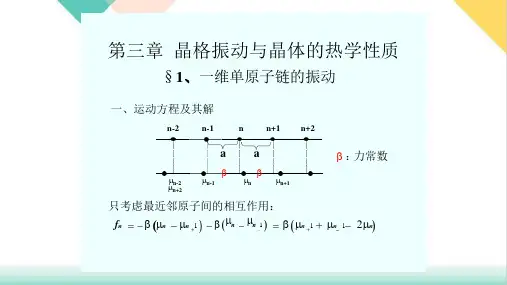

第三章 晶格振动与晶体热力学性质3-1 一维晶格的振动一、 一维单原子链(简单格子)的振动 1. 振动方程及其解(1)模型:一维无限长的单原子链,原子间距(晶格常量)为a ,原子质量为m 。
用xn 和xk 分别表示序号为n 和k 的原子在t 时刻偏离平衡位置的位移,用x nk = x n -x k 表示在t 时刻第n 个和第k 个原子的相对位移。
(2)振动方程和解平衡时,第k 个原子与第n 个原子相距0r a k n =-)(r u 为两个原子间的互作用势能,平衡时为)(0r u ,t 时刻为)()(0r r u r u δ+=)()(0r r u r u δ+=⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=3332220)(d d 61)(d d 21d d )(000r r u r r u r r u r u r r r δδδ ⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=3332220000d d 61d d 21d d )()(nk r nk r nk r x r u x r u x r u r u r u 第 n 个与第 k 个原子间的相互作用力:⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-=2332200d d 21d d d d nk r nk r nkx r u x r u r u f 振动很微弱时,势能展开式中忽略掉(δr )二次方以上的高次项---简谐近似。
(忽略掉作用力中非线性项的近似---简谐近似。
) 得: nk nk r nkx x r u f β-=⎪⎪⎭⎫ ⎝⎛-=022d d 022d d r r u ⎪⎪⎭⎫⎝⎛=β()k n kn x x f --=∑β原子的振动方程: ()k n knx x mx--=∑β..只考虑最近邻原子间的相互作用,且恢复力系数相等:()()11..+-----=n n n n x x x x n m x ββ ()11..2+----=n n n x x x nm x β给出试探解:()naq t i n A x --=ωe ])1([1e aq n t i n A x +--+=ω原子都以同一频率ω,同一振幅A 振动,其中naq 表示第n 个原子在t=0时刻的振动相位,相邻原子间的位相差为aq 。