当前位置：文档之家 › 固体物理第二章第四节 倒格子

固体物理第二章第四节 倒格子

  • 格式：ppt
  • 大小：803.00 KB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

固体物理学-倒格子

固体物理学-倒格子

《固体物理学》 固体物理学》
§3 倒格子
证明： 证明：
v v a i gb j = 2πδ ij
如果所考虑的体系足够大，忽略表面效应， 如果所考虑的体系足够大，忽略表面效应，布拉 菲格子满足平移对称性要求，对应点的物理化学性质， 菲格子满足平移对称性要求，对应点的物理化学性质， 如质量、密度、电子云密度、原子实产生的势场等， 如质量、密度、电子云密度、原子实产生的势场等， 亦为周期函数，一般地写成： 亦为周期函数，一般地写成：
v u v v Γ r + R n = Γ r L L L L (1)
(
) ()
u v v v v 其中， 其中，R n = n1 a1 + n2 a 2 + n3 a 3
v 将 Γ r 展成傅里叶级数
()
v u iG h gr v uv v Γ r = ∑ A Gh e L L L L L L L ( 2)
g u v v u v v −iG h gr 1 A Gh = ∫ Γ r e L L L L L L ( 3) Ω Ω Ω为原胞体积， ) 式意味着，对所有布拉菲格子的所有格矢，应有 (1 u v v u v v u − iG h gr v 1 A Gh = ∫ Γ r + R n e dr L L L L L L ( 4 ) Ω Ω uv v u v / 引入r = r + R n , ( 4 ) 式化为 u v uv uu/v u u v v u u v v u v u v iG h gRn 1 / − iG h gr / iG h gR n A Gh = ∫ Γ r e dr ge = A Gh e L L L L L ( 5) Ω Ω 即： u u v v u v iG h gR n A G h 1 − e = 0L L L L L L L L ( 6 )
固体物理第二章第四节 倒格子

固体物理第二章第四节 倒格子


1 ig r ig Rn 1 ig r ig Rn A( g ) F (r )e e dr F (r )e dr e


A( g ) 0 or
g
A( g )
定义对布拉维格子中所有格矢满足或或m为整数的全部端点的集合构成该布拉维格子称为正格子的倒格子reciprocallattice与倒格子的定义对应由格矢的端点所描述的布拉维格子称为正格子directlattice由端点的集合所描述的布拉维格子称为倒格子reciprocallattice称为倒格矢利用倒格矢满足的傅里叶展开为
ig Rn ig Rn A( g ) A( g )e A( g )[1 e ] 0 ig Rn
ig r F (r ) A( g )e 0

e
1
不合要求，应舍去
所以
e
ig Rn
1
ig Rn 也就是说,一定存在某些 g 使得当 e 1 成立时
同理可得 b2 , b3
所以倒格子基矢与正格子基矢的关系为：
2π b1 a2 a3 Ω 2π b2 a3 a1 Ω 2π b3 a1 a2 Ω
其中 a1 , a2 , a3 是正格基矢 Ω a1 a2 a3
则下式自然成立： n1Gh a1 n2Gh a2 n3Gh a3 2 m 或： Gh a1 2 h1; Gh a2 2 h2 ; Gh a3 2 h3 由于 a1 , a2 , a3为基矢，互不共面，则由 bi a j 2 ij 可知 b1 , b2 , b3 亦应该不共面，从 而可以用 Gh h1b1 h2b2 h3b3 描述倒格子。
固体01-04倒格子

固体01-04倒格子

a 1 ⋅ b1 = 2π a1 ⋅ b2 = 0
a i ⋅ b j = 2πδ ij =
2π ( i = j )
0 (i ≠ j )
a 2 ⋅ b1 = 0 a 2 ⋅ b2 = 2π
2π b1 = i a 2π b2 = j a
2π a
2π a
G h = h1 b1 + h2 b 2
2π 的正方形格子。 倒格是边长为 的正方形格子。 a
b1 =
2
2π
2
3
1 = a1 ⋅ a2 ×a3 = a3 2
(
)
3
1
3
1
2
a2 ×a3 =
i a 2 a 2
j a − 2 a 2
a k − a =i 2 a 2 a 2 − 2
a a 2 + j 2 a a − − 2 2
一、倒格子点阵
一个具有晶格点阵周期的函数 n(r) = n(r + R) 展开成傅里 叶级数后，其傅里叶级数中的波矢在傅里叶空间中表现为 叶级数后， 一系列规则排列的点， 一系列规则排列的点，这些点排列的规律性只决定于函数 n(r)的周期性而与函数的具体形式无关。 n(r)的周期性而与函数的具体形式无关。 的周期性而与函数的具体形式无关 我们把在傅里叶空间中规则排列着的点的列阵称为倒格子 我们把在傅里叶空间中规则排列着的点的列阵称为倒格子 点阵（或倒易点阵） 点阵（或倒易点阵）。倒格子点阵是晶体结构周期性在傅 里叶空间中的数学抽象。 里叶空间中的数学抽象。如果把晶体点阵本身看作一个周 期函数，我们可以说， 期函数，我们可以说，倒格子点阵就是晶体点阵的傅里叶 变换。反之，晶体点阵就是倒格子点阵的傅里叶逆变换。 变换。反之，晶体点阵就是倒格子点阵的傅里叶逆变换。
倒格子讲解

倒格子讲解

中文名称：倒格子英文名称：Reciprocal lattice术语来源：固体物理学倒格子，亦称倒易格子(点阵)，它在固体物理学中，特别是在晶格动力学理论、晶体电子论以及晶体衍射方面有着较为广泛的应用。

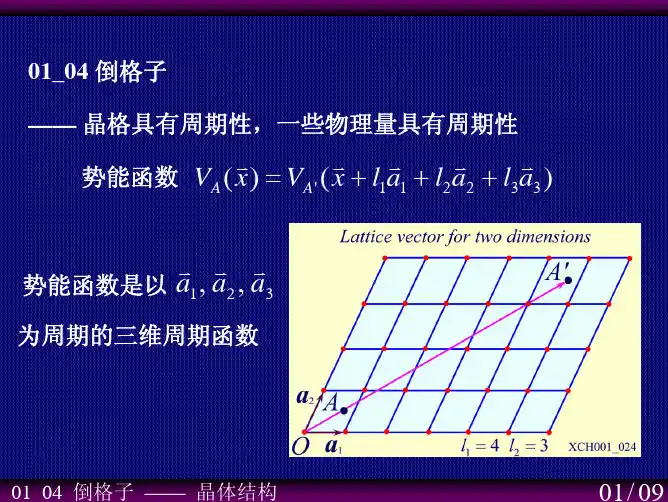
1定义假定晶格点阵基矢a1、a2、a3（1、2、3表示 a 的下标，粗体字表示a1 是矢量，以下类同）定义一个空间点阵，我们称之为正点阵或正格子，若定义b1 = 2 π ( a2× a3) /νb2 = 2 π ( a3× a1) /νb3 = 2 π ( a1× a2) /ν其中 v = a1· ( a2× a3 ) 为正点阵原胞的体积，新的点阵的基矢b1、b2、b3是不共面的，因而由b1、b2、b3也可以构成一个新的点阵，我们称之为倒格子，而b1、b2、b3 称为倒格子基矢。

2性质1. 倒格子的一个矢量是和晶格原胞中一组晶面相对应的，它的方向是该晶面的法线方向，而它的大小则为该晶面族面间距倒数的2π倍。

2. 由倒格子的定义，不难得到下面的关系a i ·b j = 2 πδij3. 设倒格子与正点阵（格子）中的位置矢量分别为G = αb1+ βb2 + γb3R = ηa1 + θa2 + λa3 (α,η,β,θ,γ,λ皆为整数)不难证明G·R = 2π ( αη + βθ +γλ ) = 2π n，其中n为整数。

4. 设倒格子原胞体积为ψ，正格子原胞体积为 v ，根据倒格子基矢的定义，并利用矢量乘法运算知识，则可得到ψ v = ( 2 π )^3.5. 正格子晶面族(αβγ)与倒格子矢量G = αb1+ βb2 + γb3 正交（具体的内容及证明过程，请参考文献[1]）3倒格子引入的意义这里简单的说一点，如上面的性质1，倒格子中的一个基矢对应于正格子中的一族晶面，也就是说，晶格中的一族晶面可以转化为倒格子中的一个点，这在处理晶格的问题上有很大的意义。

第二章++X射线衍射和倒格子

第二章++X射线衍射和倒格子

第⼆章++X射线衍射和倒格⼦第⼆章 X 射线衍射和倒格⼦⼤多数探测晶体中原⼦结构的⽅法都是以辐射的散射概念为基础的。

早在1895年伦琴发现X 射线不久，劳厄在1912年就意识到X 射线的波长量级与晶体中原⼦的间距相同，⼤约是0.1nm 量级，晶体必然可以成为X 射线的衍射光栅。

随后布拉格⽤X 射线衍射证明了NaCl 等晶体具有⾯⼼⽴⽅结构，从⽽奠定了⽤X 射线衍射测定晶体中的原⼦周期性长程有序结构的地位。

随着科学技术的不断发展，电⼦、中⼦衍射有为⼈类认识晶体提供了有效的探测⽅法。

但到⽬前为⽌，X 射线衍射仍然是确定晶体结构、甚⾄是只具有短程有序的⽆定形材料结构的重要⼯具。

本章以X 射线衍射为例介绍晶体的衍射理论，引⼊倒格⼦的概念，在此基础上介绍原⼦形状因⼦和⼏何结构因⼦，并介绍⼏种确定晶格结构的实验⽅法。

§2.1 晶体衍射理论⼀、布拉格定律（Bragg ’s Law ）X 射线是⼀种可以⽤来探测晶体结构的辐射，其波长可以⽤下式来估算012.4()()hcE h A E KeV νλλ==?= （2.1.1）能量为2~10KeV 的X 射线适⽤于晶体结构的研究。

在固体中，X 射线与原⼦的电⼦壳层相互作⽤，电⼦吸收并重新发射X 射线，重新发射的X 射线可以探测得到，⽽原⼦核的质量相对较⼤，对这个过程没有响应。

X 射线的反射率⼤约是10-3~10-5量级，在固体中穿透⽐较深，所以X 射线可以作为固体探针。

1912年劳厄（/doc/eb1ccaba1a37f111f1855b71.html ul ）等发现了X 射线通过晶体的衍射现象之后，布拉格（W.L.Bragg ）⽗⼦测定了NaCl 、KCl 的晶体结构，⾸次给出了晶体中原⼦规则排列的实验数据，发现了晶态固体反射X 射线特征图像，推导出了⽤X 射线与晶体结构关系的第⼀个公式，著名的布拉格定律（Bragg ’s Law ）。

布拉格对于来⾃晶体的衍射提出了⼀个简单的解释。

固体物理学 倒格子

固体物理学 倒格子

(2π ) v v v v = 2 ( a2 × a3 ) ⋅ a1 v0
3 * 0
(2π ) v = v0
* 0
3
01 04 倒格子 —— 晶体结构
2) 正格子中一簇晶面 ( h1 h2 h3 ) 和
v Gh1h2h3 正交
v v v v Gh1h2h3 = h1b1 + h2b2 + h3b3
—— 积分在一个原胞中进行
01 04 倒格子 —— 晶体结构
—— 倒格子与正格子间的关系 1) 正格子原胞体积反比于倒格子原胞体积
v v v * v0 = b1 ⋅ (b2 × b3 )
3
v v v v v v v v v A × B × C = ( A ⋅ C ) B − ( A ⋅ B )C
(2π ) v v v v v v = ( a2 × a3 ) ⋅ ( a3 × a1 ) × ( a1 × a2 ) 3 v0
v v v a2 × a3 b1 = 2π v v v a1 ⋅ a2 × a3
v v v v v v a3 × a1 a1 × a2 b2 = 2π v v v b3 = 2π v v v a1 ⋅ a2 × a3 a1 ⋅ a2 × a3
v v v 以 b1 , b2 , b3 为基矢构成一个倒格子
01 04 倒格子 —— 晶体结构
v 3) 倒格子矢量 Gh1h2h3 为晶面( h1h2 h3 ) 的法线方向
v v v v 晶面方程 ( h1b1 + h2b2 + h3b3 ) ⋅ x = 2πn
各晶面到原点O点的距离
v v v (2π n ) / h1b1 + h2b2 + h3b3
v v ai ⋅ b j = 2πδ ij
倒格子

倒格子

倒格子（倒易点阵） 倒格子（倒易点阵）
倒格子的定义： 倒格子的定义：
• 在固体物理学中：实际观测无法直接测量 在固体物理学中： 正点阵， 正点阵，倒格子的引入能够更好的描述很 多晶体问题， 多晶体问题，更适于处理声子与电子的晶 格动量。 格动量。 • 在X射线或电子衍射技术中：一种新的点阵， 射线或电子衍射技术中： 射线或电子衍射技术中 一种新的点阵， 该点阵的每一个结点都对应着正点阵中的 一个晶面，不仅反映该晶面的取向， 一个晶面，不仅反映该晶面的取向，还反 映着晶面间距。 映着晶面间距。
b1 =
2
(a ×a ) a ⋅ (a ×a ) 1 (a ×a ) b = a ⋅ (a ×a )
1
2 2 3 1 3 3 1
b3 =
(a ×a ) a ⋅ (a ×a )
1
1 1 2 3 2
2
3
1
确定倒格矢的方法：对于一切整数 h,k,l,作出 作出 ( hb1 + k b 2 + l b3),这些向 这些向 量的终点就是倒格 子的节点。 子的节点。
倒格子（倒易点阵）的基本性质： 倒格子（倒易点阵）的基本性质：
• 正点阵与倒易点阵的同名基矢的点积为 ，不同 正点阵与倒易点阵的同名基矢的点积为1， 名基矢的点积为零； 名基矢的点积为零； • 正点阵晶胞的体积与倒易点阵晶胞的体积成倒数 关系； 关系； • 正点阵的基矢与倒易点阵的基矢互为倒易； 正点阵的基矢与倒易点阵的基矢互为倒易； h • 任意倒易矢量（ b1 + kb2 + lb3 ）垂直于正点阵中的 任意倒易矢量（ （hkl）面； ） • 倒易矢量的模等于正点阵中晶面间距的倒数。 倒易矢量的模等于正点阵中晶面间距的倒数。
• 任何一个晶体结构都有两个格子：一个是 任何一个晶体结构都有两个格子： 正格子空间(位置空间 位置空间)， 正格子空间 位置空间 ，另一个为倒格子空 状态空间)。 间(状态空间 。二者互为倒格子，通过傅里 状态空间 二者互为倒格子， 叶变换。 叶变换。晶格振动及晶体中电子的运动都 是在倒格子空间中的描述。 是在倒格子空间中的描述。
固体物理(第4课)倒易空间课件

固体物理(第4课)倒易空间课件


V* b1 (b2 b3 )
(2 )3
V
可见V*与V互为倒数
上式利用了 A B C ( A C)B ( A B)C
(4) 倒格矢和正点阵晶面族之间的关系：
正点阵中一族晶面，晶面指数为：（h1h2h3）
倒易点阵中倒格矢：
Gh
h1b1 h2b2
h3b3
则有：
GGhh
Γ (r)为周期函数
将Γ (r)作傅里叶级数展开，有：
Γ (r)＝ C e C e n1 n2 n3
iGn
r
n
n
iGn
r
n
n1 n2 n3
n
学习交流PPT
11总Biblioteka ：晶体点阵 实际晶体结构显微图像 微观粒子 线度量纲：L 位置空间 坐标空间
倒易点阵 虚构
衍射图像 一族晶面 线度量纲：L－1 倒易空间 傅里叶空间
aa13aa33
2
a
2
a
i j
离原点最近的倒 格点有４个： b1，-b1，b2，-b2．
-b1
b2
b1 －b2
学习交流PPT
14
离原点次近的倒
格点有４个：
b1＋b2 ，b1-b2 ，
b2，-b2．
-b1＋b2
b1＋b2
－b1-b2
b1-b2
学习交流PPT
15
离原点再远的倒格点有４个：
２b1，-２b1，２b2，-２b2．
Z
h1、h2、h3 Z
结论： 若两矢量点积为2的整数倍， 且其中一个矢量
为正点阵位矢， 则另一个矢量必为倒易点阵的位矢。
学习交流PPT
7
•为什么在倒易关系中存在2π 因子，这是因为如此定 义的互为倒易的两个矢量G与T之间满足下面简洁的
固体物理学：倒格子

固体物理学：倒格子


[1]倒格子基矢与正格子基矢的关系------两个基矢正交
设
Gh1h2h3
h1b1 h2b2
所以，Gh1h2h3 • Rl1l2l3 (h1b1
h3b3 h2b2
h3b3 )
•
(n1a1
n2a2
n3a3
)
由此推论：
bi
•
aj
2m 2 ij
[2]倒格子与正格子的原胞体积的关系
G a3 h3 2
由此上式可表示为：G h1b1 h2b2 h3b3
ai bj
2 i j
0 i j i, j 1,2,3
b1
b2
b3
2
V
2
V
2
V
(a2
(a3 (a1
a3 )
a1 )
a2 )
V a1 (a2 a3 )
是原胞的体积
以 b1 ，b2，b3 作为基矢所构成的格子称倒格子。
正格子体积为 倒格子体积为
a1 • (a2 a3 ) b1 • (b2 b3)
(3) 倒格子矢量与晶面指数的关系---倒格矢的方向
如图所示，晶面系 (hlh2h3)中最靠近 原点的晶面ABC在基 矢a1 , a2 , a3上的截 距分别是a1/hl， a2/h2，a3/h3。
结论： 倒格矢G垂直于密勒指数为（h1h2h3）晶 面系(倒格式的方向)。或倒格矢G为晶面（h1h2h3）
Hale Waihona Puke 就是倒格子点阵的傅里叶逆变换。
理解（2）
晶格点阵（或叫正格子点阵）是真实空间中的点阵， 具有[长度]的量纲；
倒格子点阵（或叫倒易点阵）是在与真实空间相联系 的傅里叶空间中的点阵，具有[长度]-1的量纲。量纲为L-1 的矢量空间为倒格子空间。
固体物理之之倒格子

固体物理之之倒格子

倒格子题目：试论倒格子、倒格子空间的基本概念、与正格子的关系以及在固体物理研究中的意义和作用。

1.倒格子的基本概念：假定晶格点阵基矢1a 、2a 、3a（1、2、3表示 a 的下标）定义一个空间点阵，我们称之为正点阵或正格子，若定义： v a a b )(2321 ⨯=π v a a b )(2232 ⨯=π v a a b )(2213 ⨯=π其中)(321a a a v ⨯⋅= 为正点阵原胞的体积，新的点阵的基矢1b 、2b 、3b 是不共面的，因而由 1b 、2b 、3b 也可以构成一个新的点阵，我们称之为倒格子 ，而1b 、2b 、3b 称为倒格子基矢。

2.倒格子与正格子之间的关系：①基矢间关系：3,2,1,)(0)(2=⎩⎨⎧≠==*j i j i j i b a j i π ②位矢之间关系：正格子位矢：332211a l a l a l R l ++=倒格子位矢：332211b n b n b n G n ++=二者关系：m R G l n π2=⋅ （m 为整数）表明：若两矢量点积为π2的整数倍，则其中一个矢量为正格子位矢， 另一个必为倒格子位矢。

③原胞体积的关系：倒格子原胞的体积v *与正格子原胞体积v 的关系 为:)()2()2()(32133321*a a a vb b b v ⨯⋅==⨯⋅=ππ ④倒格矢332211b h b h b h G ++=与正格子中密勒指数为)(321h h h 的晶面族正交。

即332211b h b h b h G ++=沿晶面族)(321h h h 的法线方向。

3.固体物理研究中的意义和作用：①：倒格子中的一个基矢对应于正格子中的一族晶面，也就是说，晶格中的一族晶面可以转化为倒格子中的一个点，这在处理晶格的问题上有很大的意义。

例如，晶体的衍射是由于某种波和晶格互相作用，与一族晶面发生干涉的结果，并在照片上得出一点，所以，利用倒格子来描述晶格衍射的问题是极为直观和简便的。

固体物理学-倒空间

固体物理学-倒空间


倒格与正格基矢的关系
՜ ՜
ℎ ⋅ = 2π
ℎ‘ =ℎ1 1 + ℎ2 2 + ℎ3 3
(1 റ1 + 2 റ 2 + 3 റ 3 ) ⋅ (ℎ1 ′1 + ℎ2 ′2 + ℎ3 ′3 ) = 2
两种点阵的基矢之间的关系：
Solid State Physics
2
Solid State Physics
倒格矢与傅里叶变换
在任意两个原胞的相对应点上，晶体的物理性质相同。
՜
՜
՜
Γ + = Γ
上式两边分别按傅里叶级数展开：
՜ ՜
ℎ ⋅ = 2π
倒格矢是傅里叶空间的矢量，它取决于正格子点阵的周期性
倒格空间=傅里叶空间
Solid State Physics
衍射加强条件的另外一种形式：
相位差
∆∅ =

λ
2 =
2
波矢 0 = 0
λ
∙− ∙0
λ
2= 2
2
=
റ
λ
՜ ՜
՜
⋅ − 0 = 2πμ
量纲互逆
∙ ℎ’ = 2
՜ ՜
՜
− 0 = ℎ′
倒格矢
ℎ ℎ
倒格空间=波矢k空间（动量 = = ）
՜
՜
՜
则， 1 ， 2 ， 3 分别与(100), (010), (001)晶面族正交
(1) 倒易点阵的一个基矢是与正点阵的一组晶面相对应的；
(2) 倒易点阵基矢的方向是该晶面的法线方向；
՜
՜
՜
՜
ℎ = ℎ1 1 + ℎ2 2 + ℎ3 3 的长度为

固体物理_倒格子与布里渊区_2013


a3 (a1 a2 )
所以：
a3 b3 2
a3 b1/ 2 0
采用同样的方法，我们可以得出：
a2 b2 2 a2 b1/3 0
2 ( a 3 a1 ) b2 2 ( a 2 a3 ) b1
二、特性：
1、第一布里渊区： 在倒格子点阵中，做某一倒格点到其最近邻 倒格点连线的垂直平分面，由这些垂直平分面所 围成的多面体就是第一布里渊区。 除第一布里渊区之外,还有第二布里渊区、第 三布里渊区以及更高阶的布里渊区。
晶面:(111) 面间距：
n
(111)
(111)
法线方向： n
3 a 3
2 2 2 kh i j k 倒格矢： a a a
b3
b2 b1
2 3 k a 面间距： h k 3 h h 法线方向： k i jk kh
三、正格子和倒格子的相互关系
右手定律
2、验证：倒格矢能代表一族晶面吗？
晶面族(h1h2h3) 中最 靠近坐标原点的晶面 ABC在基矢 a1 , a2 , a3
a1 a2 a3 上的截距为 , , h1 h2 h3
kh (1)倒格矢Kh垂直与晶面族 n kh
2 (2)倒格矢的模量等于面间距的倒数成正比。 k h d
3
正格子元胞与倒格 子元胞体积成反比
课堂练习：
试证体心立方格子和面心立方格子互为正、倒格子。
面心立方晶格的初基原胞基矢为：P10 体心立方晶格的初基原胞基矢为：P10 a a a1 ( j k ) a1 (i j k ) 2 2 a a a2 (i j k ) a2 (k i ) 2 2 a a a3 (i j k ) a3 (i j ) 2 2 面心立方晶格的倒格子基矢如下：

固体物理第二章


由于k0=2π/ λ, (2)式:
R ∙(k0 - k)=2 πn
由平移矢量R和倒格式G的关系: R ∙G=2 πm (3) 比较(2)和(3): k0 – k=G (4)
(4)被称为劳厄方程
4.衍射极大条件 劳厄方程 （Laue Equation） a. 坐标空间中的劳厄方程
晶格中任一格点为O，格点A的位矢 Rl=l1a1+l2a2+l3a3, S0和S为单位矢量。 光程差 衍射加强的条件 A
可以证明，每个布里渊区的体积均相等，都等于第一布里渊区的体积， 即倒格子原胞的体积b
立方晶系的简约区
正格子 格常数 倒格子 格常数 简约区
sc
a
sc
2 a
由6个{100}*面 围成的立方体
由12个{110}*面 围成的菱形12面体 由8个{111}*面和6个{100}*面围 成的14面体
bcc
S=2f 当v1 ＋v2 ＋v3＝偶数
7. 晶体衍射
当辐射的波长与晶格中原子间距可以比较或更小时，可发生显著的衍射现象 。 （1）x射线 一种电磁波，由被高电压加速了的电子撞击靶极物质产生。X射线的光子能量为：
SG=celldV j nj(r-rj) exp(-iG•r)
= j exp(-iG•rj) dV nj() exp(-iG• ),
= r-rj . 原子形状因子 (atomic form factor) : fj= dV nj() exp(-iG• ), SG= j fj exp(-iG•rj) rj =xja1+ yja2+ zja3 , G= v1b1+ v2b2+ v3b3 SG(v1 v2 v3) = j fj exp[-2 i (v1xj + v2yj +v3zj )] 例如：体心立方 S=0 当v1 ＋v2 ＋v3＝奇数

固体物理倒格子的原理

倒格子摘要：倒格子是现在固体物理，半导体物理，器件物理的前沿，用量子场论的非相对论形式描述多体，各种散射过程的精确描述都少不了它。

为此为了研究的方便，结晶学家喜欢用正格子，而物理学家喜欢用倒格子，因为它在数学处理上具有优越性。

和正格子相比，它在固体物理学中，特别是在晶格动力学理论、晶体电子论以及晶体衍射方面有着较为广泛的应用。

因此倒格子具有很重要的物理意义，及其所组成的倒易点阵，更是研究晶格性质的重要手段。

关键词：倒格子正格子点阵布里渊区一、倒格子的定义及其相关概念：（1）倒格子：亦称倒易格子(点阵)，倒格子就是和布拉发矢量（晶格矢量）共轭的另一组矢量基，俗称动量空间，适合于用来描述声子、电子的晶格动量。

它在固体物理学中，特别是在晶格动力学理论、晶体电子论以及晶体衍射方面有着较为广泛的应用。

是现在固体物理，半导体物理，器件物理的前沿，用量子场论的非相对论形式描述多体，各种散射过程的精确描述都少不了它。

晶格振动及晶体中电子的运动都是在倒格子空间中的描述。

（2）倒格子的定义：已知有正格子基矢，定义倒格矢基矢为：；说明b1垂直于a2和a3所确定的面。

；说明b2垂直于a3和a1所确定的面。

；说明b3垂直于a1和a2所确定的面。

正格子体积：（3）相关概念：①倒格点：平移操作所产生的格点叫。

②倒格矢：为。

③倒格子：倒格点的总体叫。

④倒格基矢：一组。

二、倒格子的性质：（1） 正点阵晶胞的体积与倒易点阵晶胞的体积成倒数关系：倒格子体积： ，（2） 正格子与倒格子间的关系：倒格矢与任一个正格矢的乘积必等于, 即 = 。

（3） 正格子中一族晶面（321h h h ）和倒格子基失矢正交，即晶面的弥勒指数是垂直于该晶面的最短倒格矢坐标。

（4） 倒格子的一个基矢是和晶格原胞中一组晶面相对应的，它的方向是该晶面的法线方向；倒格矢的大小正比于晶面族（h1h2h3）的面间距的倒数：dG π2//=三、倒格子原胞和布里渊区：倒格子原胞，作由原点出发的诸倒格矢的垂直平分面，这些平面完全封闭形成的最小的多面体（体积最小）------第一布里渊区。

第二章——晶体衍射和倒格子


1.
K n h1b1 h2 b2 h3 b3
2.与晶体中一族晶面相 对应； 3.是与真实空间相联系的 傅里叶空间中点的周期性 排列； 4.线度量纲为[长度]-1
4
晶体 结构
求解倒格
正格 基矢 倒格 基矢
正格
倒格
2π b1 a2 a3 Ω 2π b2 a3 a1 Ω 2π b3 a1 a2 Ω
R l K h 2π
(为整数)
其中 R l 和K h 分别为正格点位矢和倒格点位矢。
a1 l2 a 2 l3 a3 R l l1
b1 h2 b 2 h3 b3 K h h1
b 1 h2 b 2 h3 b3 ) a1 l2 a 2 l3 a 3 ) ( h1 R l K h ( l1
*
3


3
（ 4）
倒格矢 K h h1 b1 h2 b 2 h3 b 3 与正格中晶面族(h1h2h3) 正交，且其长度为
2π d h1h2 h3
。
a） 证明 K h h b1 h b 2 h b 3 与晶面族(h1h2h3)正交。 1 2 3
b） 证明
K h h1 b1 h2 b 2 h3 b 3
Statement: the Fourier transform of a function:
ik r e f (r ) f k k
To a periodic function in Bravais lattice:
ik r ik r R ik r ik R f (r ) f (r R) f k e f k e f k e e
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
波矢k可用来描述波的传播方向.那么晶体结 构的周期性是否也可以用波矢k来描述呢？如 果可以,在波矢k空间,k应满足什么条件呢？
布拉维格子具有平移对称性,因而相应的只与 位置有关的物理量,由于布拉维格点的等价性,均 应是布拉维格矢R的周期函数,如：格点密度、质 量密度、电子云密度、离子实产生的势场等都是
第四节 倒格子
本节主要内容: 一、 概念的引入 二、 倒格子是倒易空间的布拉维格子 三、 倒格矢与晶面 四、 倒格子的点群对称性
§2.4 倒格子
一、概念的引入 晶体结构的周期性,可以用坐标空间(r空间)的 布拉维格子来描述,这是前几节我们所讨论的内 容,也是我们易于理解的实物粒子的普遍描述.
然而,量子力学的学习使我们认识到,任何基本 粒子都具有波粒二象性.亦即具有一定能量和动 量的微观粒子,同时也是具有一定的波长和频率 的波,波也是物质存在的一种基本形式.
原胞体积
所以：A(g v) 1F(rvR vn)eig v•rvdrv
令 rvrvRvn 则：r v r v R v n d r v d r v
则 A (g v ) 1F ( r v ) e ig v • (r v R v n )d r v 1F ( r v ) e ig v • r v e ig v • R v n d r v
二、 倒格子是倒易空间的布拉维格子
或对G v布h•拉R vn维格2子m,中(所m为有整格数矢)的Rv n 全，部满G足v h 端eiGv点h•Rv的n 集1
合，构成该布拉维格子，称为正格子的倒格子 v
(re将cipR v rn o can l1 a lv a1 t tin c2 ea v )2 . G n h 3 称a v 3 为代倒入格G 矢vh•R vn2m,
A (g v ) 1 F (r v )e ig v • r v e ig v • R v n d r v 1 F (r v )e ig v • r v d r v e ig v • R v n
A ( gv)
A ( g v ) A ( g v ) e i g v • R v n A ( g v ) [ 1 e i g v • R v n ] 0
G v hh 1 b v 1h 2b v 2 对h 3 b v 3
应的是倒易空间中的布拉维格子，亦即倒格子
A (g v ) 0 o r e ig v • R v n 1
F(rv) A(gv)eigv•rv0 不合要求，应舍去
gv
所以 eigv•Rvn 1
也就是说,一定存在某些 gv使得当 eigv•成Rvn 立1时
F(rv)F(rvR vn)成立
由于 g与v
格子,自然
存也Rv n 在可上以gv 述描对述应同关样系的,布可拉以Rv维n 描格述子布 Nhomakorabea且拉维与
倒格子(reciprocal lattice)
v G h 称为倒格矢
利用倒格矢，满足 F(rv)F 的(傅rv 里R 叶vn)展
开为:
F(rv)
v
v A(Gh
v
)eiGh
•rv
Gh
v 1
A(Gh)
F(rv)eiGvh•rvdrv
意义：把上述满足坐标空间中的某物理量转
变为倒格子空间,且只存在波矢为倒格矢的分量。
或： G v h • a v 1 2 h 1 ; G v h • a v 2 2 h 2 ; G v h • a v 3 2 h 3
由于 a为v1,基av2,矢av3，互不共面，则由
描bvi •述av倒j 格2可子G v 知h 。ij h 1 b v 1 亦h 2 bb v v应12 , bv该2h ,3 b b不v v3 3 共面，从而可以用
得： n 1 G v h • a v 1 n 2 G v h • a v 2 n 3 G v h • a v 3 2 m
欲使上式恒成立，且考虑到n1,n2,n3为任意
整数，则要求： G v h • a v 1 2 h 1 ; G v h • a v 2 2 h 2 ; G v h • a v 3 2 h 3
h1,h2,h3为整数
v vvv
显然,如果令 G h h 1 b 1 h 2 b 2 h 3 b 3h1,h2,h3为整数
当 b v i• a v j 2i j;i 1 ,2 ,3 ;j 1 ,2 ,3 满足时，
则下式自然成立：
n 1 G v h • a v 1 n 2 G v h • a v 2 n 3 G v h • a v 3 2 m
如此。F(rv 不)失 一F 般(性rv， 上R v 述n函)数布可拉统维一格写矢为：
1. 周期函数的傅里叶展开
由于F(r)是布拉维格矢R的周期函数,所以可以将
其展开成傅里叶级数：
F(rv) A(gv)eigv•rv gv
展开系数
展开系数
A(gv)1 F(rv)eigv•rvdrv
因为：F (r v)F (r vR v n)
第一gv 章讨论自由电子的波函数中的波矢类似,因
而,凡是波矢 和布拉gv 维格矢满足
eigv•Rvn 的1
波矢,一定也可以描述布拉维格子.这就是倒格子
的由来. c o s ( g v • R v n ) 1 g v • R v n 2 m ; w h e r e m i s i n t e g e r
2. 定义
或对G v布h•拉R vn维格2子m,中(所m为有整格数矢)的Rv n 全，部满G足v h 端eiGv点h•Rv的n 集1
合，构成该布拉维格子，称为正格子的倒格子
(reciprocal lattice)
v
与倒格子的定义对应，由格矢 的R n 端点所描述
的由布拉Gv端维h 点格的子集，合称所为描正述格的子布(d拉ire维ct格lat子tic，e)称为
v vvv
由于 G h h 1 b 1 h 2 为b 2倒 h 格3 b 3 矢，如果把倒格矢所在
的空间称为倒格子空间，或倒易空间(reciprocal
space),则由于
不共面，bv1,自bv2然,bv3可以成为倒易
空间的基矢。
和 R v n n 1 a v 1 n 2 对a v 2比 n ,3 表a v 3明