下载文档原格式
第1篇一、实验背景随着信息技术的飞速发展，数字经济已成为推动全球经济增长的重要引擎。
为深入了解数字经济的发展现状、趋势及挑战，本实验报告以我国某数字经济实验室为研究对象，通过实地调研、数据分析等方法，对该实验室的实验项目、实验成果及实验影响进行综合分析。
二、实验目的1. 了解数字经济实验室的实验项目及研究方向。
2. 分析数字经济实验室的实验成果及社会影响力。
3. 探讨数字经济实验室在推动我国数字经济产业发展中的作用。
三、实验方法1. 实地调研：走访数字经济实验室，了解实验室的实验环境、实验设备、实验项目及实验团队。
2. 数据分析：收集实验室公开发表的实验报告、论文、项目成果等，进行统计分析。
3. 案例分析：选取实验室具有代表性的实验项目，深入分析其实验过程、实验成果及社会影响。
四、实验内容1. 实验室概况本实验室成立于20XX年，位于我国某知名高校。
实验室以数字经济为研究方向，致力于培养数字经济领域的专业人才，推动数字经济产业发展。
2. 实验项目及研究方向（1）大数据分析：利用大数据技术，对海量数据进行分析，挖掘有价值的信息，为政府、企业及个人提供决策支持。
（2）人工智能：研究人工智能在数字经济领域的应用，如智能推荐、智能客服、智能金融等。
（3）区块链技术：研究区块链技术在数字经济领域的应用，如供应链金融、数字货币等。
（4）物联网：研究物联网在数字经济领域的应用，如智能家居、智能交通等。
3. 实验成果及社会影响力（1）培养数字经济人才：实验室培养了一大批数字经济领域的专业人才，为我国数字经济产业发展提供了人才支持。
（2）推动产业创新：实验室的研究成果在多个领域得到应用，推动了相关产业的创新发展。
（3）提升企业竞争力：实验室与企业合作，为企业提供技术支持，帮助企业提升竞争力。
（4）促进政策制定：实验室的研究成果为政府制定相关政策提供了参考依据。
4. 典型实验项目分析（1）项目背景：某企业希望通过大数据分析，提升客户满意度，降低客户流失率。
python数字实验报告Python数字实验报告引言：Python是一种功能强大的编程语言，它提供了丰富的数字处理功能。
本文将通过一系列实验，探索Python中数字的特性和应用。
我们将介绍数字的基本操作、数值类型转换、数学函数、随机数生成以及数据可视化等方面的内容。
一、数字的基本操作Python中的数字类型包括整数（int）、浮点数（float）和复数（complex）。
我们可以使用基本运算符（如加减乘除）对数字进行操作，并通过变量来存储和使用数字。
Python还提供了丰富的数学函数库，如math模块，可以进行更复杂的数值计算。
二、数值类型转换在实际应用中，我们常常需要将数字从一种类型转换为另一种类型。
Python提供了一些内置函数，如int()、float()和complex()，可以实现不同数值类型之间的转换。
我们可以利用这些函数来处理数据类型不一致的情况，确保数值计算的准确性。
三、数学函数的应用数学函数是Python中的重要工具，它们可以帮助我们解决各种实际问题。
例如，我们可以使用math模块中的函数计算三角函数、指数函数、对数函数等。
这些函数可以在科学计算、数据分析、图像处理等领域发挥重要作用。
四、随机数生成随机数在计算机科学和统计学中有着广泛的应用。
Python中的random模块提供了生成随机数的函数。
我们可以通过random模块生成伪随机数序列，并利用这些随机数进行模拟实验、随机抽样等操作。
同时，我们还可以设置随机数的种子，以确保实验的可重复性。
五、数据可视化数据可视化是数据分析中的重要环节。
Python中的matplotlib库可以帮助我们生成各种图表，如折线图、散点图、柱状图等。
通过可视化手段，我们可以更直观地分析和展示数据，从而得到更深入的洞察。
结论：通过本次实验，我们深入了解了Python中数字的特性和应用。
我们学习了数字的基本操作、数值类型转换、数学函数、随机数生成以及数据可视化等方面的知识。
数字逻辑实验报告数字逻辑实验报告引言数字逻辑是计算机科学中的重要基础知识，通过对数字信号的处理和转换，实现了计算机的高效运算和各种复杂功能。
本实验旨在通过实际操作，加深对数字逻辑电路的理解和应用。
实验一：二进制加法器设计与实现在这个实验中，我们需要设计一个二进制加法器，实现两个二进制数的加法运算。
通过对二进制数的逐位相加，我们可以得到正确的结果。
首先，我们需要将两个二进制数输入到加法器中，然后通过逻辑门的组合，实现逐位相加的操作。
最后，将得到的结果输出。
实验二：数字比较器的应用在这个实验中，我们将学习数字比较器的应用。
数字比较器可以比较两个数字的大小，并输出比较结果。
通过使用数字比较器，我们可以实现各种判断和选择的功能。
比如，在一个电子秤中，通过将待测物品的重量与设定的标准重量进行比较，可以判断物品是否符合要求。
实验三：多路选择器的设计与实现在这个实验中，我们需要设计一个多路选择器，实现多个输入信号中的一路信号的选择输出。
通过使用多路选择器，我们可以实现多种条件下的信号选择，从而实现复杂的逻辑控制。
比如，在一个多功能遥控器中，通过选择不同的按钮，可以控制不同的家电设备。
实验四：时序电路的设计与实现在这个实验中，我们将学习时序电路的设计与实现。
时序电路是数字逻辑电路中的一种重要类型，通过控制时钟信号的输入和输出，实现对数据的存储和处理。
比如，在计数器中，通过时序电路的设计，可以实现对数字的逐位计数和显示。
实验五：状态机的设计与实现在这个实验中，我们将学习状态机的设计与实现。
状态机是一种特殊的时序电路，通过对输入信号和当前状态的判断，实现对输出信号和下一个状态的控制。
状态机广泛应用于各种自动控制系统中，比如电梯控制系统、交通信号灯控制系统等。
实验六：逻辑门电路的优化与设计在这个实验中，我们将学习逻辑门电路的优化与设计。
通过对逻辑门电路的布局和连接方式进行优化，可以减少电路的复杂性和功耗，提高电路的性能和可靠性。
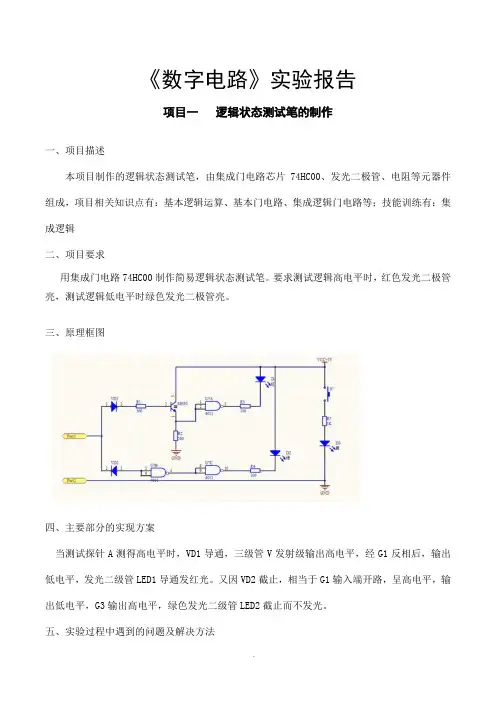
《数字电路》实验报告项目一逻辑状态测试笔的制作一、项目描述本项目制作的逻辑状态测试笔，由集成门电路芯片74HC00、发光二极管、电阻等元器件组成，项目相关知识点有：基本逻辑运算、基本门电路、集成逻辑门电路等；技能训练有：集成逻辑二、项目要求用集成门电路74HC00制作简易逻辑状态测试笔。
要求测试逻辑高电平时，红色发光二极管亮，测试逻辑低电平时绿色发光二极管亮。
三、原理框图四、主要部分的实现方案当测试探针A测得高电平时，VD1导通，三级管V发射级输出高电平，经G1反相后，输出低电平，发光二级管LED1导通发红光。
又因VD2截止，相当于G1输入端开路，呈高电平，输出低电平，G3输出高电平，绿色发光二级管LED2截止而不发光。
五、实验过程中遇到的问题及解决方法（1）LED灯不能亮：检查硬件电路有无接错；LED有无接反；LED有无烧坏。
（2）不能产生中断或中断效果：检查硬件电路有无接错；程序中有无中断入口或中断子程序。
（3）输入电压没有反应：数据原理图有没有连接正确，检查显示部分电路有无接错；4011逻辑门的输入端有无浮空。
六、心得体会第一次做的数字逻辑试验是逻辑状态测试笔，那时什么都还不太了解，听老师讲解完了之后也还不知道从何下手，看到前面的人都起先着手做了，心里很焦急可就是毫无头绪。
老师说要复制一些文件协助我们做试验（例如：试验报告模板、试验操作步骤、引脚等与试验有关的文件），还让我们先画原理图。
这时，关于试验要做什么心里才有了一个模糊的框架。
看到别人在拷贝文件自己又没有U盘只好等着借别人的用，当然在等的时候我也画完了逻辑测试笔的实操图。
后面几次都没有过，但最后真的发觉试验的次数多了，娴熟了，知道自己要做的是什么，明确了目标，了解了方向，其实也没有想象中那么困难。
七、元器件一逻辑状态测试笔电路八、附实物图项目二多数表决器电路设计与制作一、项目描述本项目是以组合逻辑电路的设计方法，用基本门电路的组合来完成具有多数表决功能的电路。
一、实验目的本次实验旨在通过实际操作，加深对数字逻辑基本原理和设计方法的理解，提高学生在数字电路设计、仿真和调试方面的实践能力。
通过完成以下实验任务，使学生掌握以下技能：1. 理解数字逻辑电路的基本概念和原理。
2. 掌握数字逻辑电路的设计方法和步骤。
3. 学会使用仿真软件进行电路设计和仿真测试。
4. 掌握数字逻辑电路的调试和优化方法。
二、实验内容本次实验主要包含以下三个部分：1. 组合逻辑电路设计：设计一个四位加法器，并使用Logisim软件进行仿真测试。
2. 时序逻辑电路设计：设计一个简单的计数器，并使用Verilog语言进行描述和仿真。
3. 数字逻辑电路综合应用：设计一个简单的数字信号处理器，实现基本的算术运算。
三、实验步骤1. 组合逻辑电路设计（1）分析题目要求，确定设计目标和输入输出关系。
（2）根据输入输出关系，设计四位加法器的逻辑电路。
（3）使用Logisim软件搭建电路，并设置输入信号。
（4）观察仿真结果，验证电路功能是否正确。
2. 时序逻辑电路设计（1）分析题目要求，确定设计目标和状态转移图。
（2）使用Verilog语言描述计数器电路，包括模块定义、输入输出定义、状态定义和状态转移逻辑。
（3）使用仿真软件进行测试，观察电路在不同状态下的输出波形。
3. 数字逻辑电路综合应用（1）分析题目要求，确定设计目标和功能模块。
（2）设计数字信号处理器电路，包括算术运算单元、控制单元和存储单元等。
（3）使用仿真软件进行测试，验证电路能否实现基本算术运算。
四、实验结果与分析1. 组合逻辑电路设计实验结果：通过仿真测试，四位加法器电路功能正常，能够实现两个四位二进制数的加法运算。
分析：在设计过程中，遵循了组合逻辑电路设计的基本原则，确保了电路的正确性。
2. 时序逻辑电路设计实验结果：通过仿真测试，计数器电路功能正常，能够实现从0到9的计数功能。
分析：在设计过程中，正确描述了状态转移图，并使用Verilog语言实现了电路的功能。
第1篇一、实验目的1. 掌握数字电路的基本原理和设计方法。
2. 学会使用数字电路设计工具，如Proteus等。
3. 培养动手能力和问题解决能力。
4. 设计并实现一个数字灯控制电路。
二、实验原理本实验采用数字电路设计，利用计数器、译码器、驱动器等芯片实现数字灯的控制。
具体原理如下：1. 计数器：用于产生一个序列的数字信号，作为控制信号输入到译码器。
2. 译码器：将计数器的输出信号转换为相应的控制信号，控制LED灯的亮灭。
3. 驱动器：将控制信号驱动到LED灯上，实现LED灯的亮灭。
三、实验器材1. 74LS163（4位同步二进制计数器）2. 74LS221（4-16译码器）3. 74LS04（6V6非门）4. LED灯5. 跳线6. 电阻7. 555定时器8. 电源9. 实验板四、实验步骤1. 设计电路图：根据实验原理，设计数字灯控制电路的电路图。
电路图应包括计数器、译码器、驱动器和LED灯等部分。
2. 仿真测试：使用Proteus软件对设计的电路图进行仿真测试，验证电路的功能是否正常。
3. 搭建实验板：根据电路图，在实验板上搭建电路。
4. 调试电路：通过调整电路参数，使电路工作正常。
5. 实验验证：观察LED灯的亮灭情况，验证实验结果。
五、实验结果与分析1. 电路仿真结果：仿真结果显示，电路能够按照预期的工作，实现LED灯的亮灭控制。
2. 实验板搭建结果：实验板搭建成功，电路工作正常。
3. 实验验证结果：观察LED灯的亮灭情况，发现LED灯的亮灭顺序与电路设计一致。
六、实验总结1. 通过本次实验，掌握了数字电路的基本原理和设计方法。
2. 学会了使用Proteus软件进行电路仿真，提高了电路设计效率。
3. 培养了动手能力和问题解决能力，为后续的电路设计奠定了基础。
七、实验拓展1. 设计并实现一个具有多种模式的数字灯控制电路，如闪烁、渐变等。
2. 将数字灯控制电路应用于实际项目中，如家居照明、交通信号灯等。
数字系统设计及实验实验报告一、实验目的数字系统设计及实验课程旨在让我们深入理解数字逻辑的基本概念和原理，掌握数字系统的设计方法和实现技术。
通过实验，我们能够将理论知识应用于实际，提高解决问题的能力和实践动手能力。
本次实验的具体目的包括：1、熟悉数字电路的基本逻辑门、组合逻辑电路和时序逻辑电路的设计方法。
2、掌握使用硬件描述语言（如 Verilog 或 VHDL）进行数字系统建模和设计。
3、学会使用相关的电子设计自动化（EDA）工具进行电路的仿真、综合和实现。
4、培养团队合作精神和工程实践能力，提高解决实际问题的综合素质。
二、实验设备和工具1、计算机：用于编写代码、进行仿真和综合。
2、 EDA 软件：如 Quartus II、ModelSim 等。
3、实验开发板：提供硬件平台进行电路的下载和测试。
4、数字万用表、示波器等测量仪器：用于检测电路的性能和信号。
三、实验内容1、基本逻辑门电路的设计与实现设计并实现与门、或门、非门、与非门、或非门和异或门等基本逻辑门电路。
使用 EDA 工具进行仿真，验证逻辑功能的正确性。
在实验开发板上下载并测试实际电路。
2、组合逻辑电路的设计与实现设计一个 4 位加法器，实现两个 4 位二进制数的相加。
设计一个编码器和译码器，实现数字信号的编码和解码。
设计一个数据选择器，根据控制信号选择不同的输入数据。
3、时序逻辑电路的设计与实现设计一个同步计数器，实现模 10 计数功能。
设计一个移位寄存器，实现数据的移位存储功能。
设计一个有限状态机（FSM），实现简单的状态转换和控制逻辑。
四、实验步骤1、设计方案的确定根据实验要求，分析问题，确定电路的功能和性能指标。
选择合适的逻辑器件和设计方法，制定详细的设计方案。
2、代码编写使用硬件描述语言（如 Verilog 或 VHDL）编写电路的代码。
遵循代码规范，注重代码的可读性和可维护性。
3、仿真验证在 EDA 工具中对编写的代码进行仿真，输入不同的测试向量，观察输出结果是否符合预期。
第1篇一、实验背景随着信息技术的飞速发展，数字建模在各个领域中的应用越来越广泛。
数字应用建模是将现实世界的复杂问题转化为数学模型，通过计算机模拟和分析，为决策提供科学依据。
本实验旨在通过数字应用建模的方法，解决实际问题，提高学生对数学建模的理解和应用能力。
二、实验目的1. 理解数字应用建模的基本原理和方法；2. 掌握数学建模软件的使用；3. 提高解决实际问题的能力；4. 培养团队合作精神和沟通能力。
三、实验内容1. 实验题目：某城市交通流量优化研究2. 实验背景：随着城市人口的增加，交通拥堵问题日益严重。
为了缓解交通压力，提高城市交通效率，本研究旨在通过数字应用建模方法，优化该城市的交通流量。
3. 实验步骤：（1）数据收集：收集该城市主要道路的实时交通流量数据、道路长度、交叉口数量、道路等级等数据。
（2）建立数学模型：根据交通流量数据，建立交通流量的数学模型，如线性回归模型、多元回归模型等。
（3）模型求解：利用数学建模软件（如MATLAB、Python等）对建立的数学模型进行求解，得到最优交通流量分布。
（4）结果分析：对求解结果进行分析，评估优化后的交通流量分布对缓解交通拥堵的影响。
（5）模型改进：根据分析结果，对模型进行改进，以提高模型的准确性和实用性。
4. 实验结果：（1）通过建立数学模型，得到优化后的交通流量分布。
（2）优化后的交通流量分布较原始分布，道路拥堵程度明显降低，交通效率得到提高。
（3）通过模型改进，进一步优化交通流量分布，提高模型的准确性和实用性。
四、实验总结1. 本实验通过数字应用建模方法，成功解决了某城市交通流量优化问题，提高了交通效率，为城市交通管理提供了科学依据。
2. 在实验过程中，学生掌握了数学建模的基本原理和方法，熟悉了数学建模软件的使用，提高了解决实际问题的能力。
3. 实验过程中，学生学会了团队合作和沟通，提高了自己的综合素质。
五、实验心得1. 数字应用建模是一种解决实际问题的有效方法，通过建立数学模型，可以将复杂问题转化为可操作的解决方案。
数字序列实验报告数字序列实验报告引言数字序列是数学中一种重要的研究对象，它们在各个领域都有广泛的应用。
本实验旨在通过对数字序列的实验研究，探索其中的规律和特点，并对其应用进行探讨。
实验一：斐波那契数列斐波那契数列是一种经典的数字序列，它的定义方式是：第一个数是0，第二个数是1，从第三个数开始，每个数都是前两个数之和。
通过编写程序，我们生成了斐波那契数列的前100个数。
实验结果显示，斐波那契数列呈现出一些有趣的特性。
首先，数列中的每个数都是前两个数的和，这种递推关系使得数列中的每个数字都与前面的数字有着密切的联系。
其次，斐波那契数列的增长速度逐渐加快，数列中的数字呈现出明显的指数增长趋势。
这种特点在生物学、金融学等领域中都有重要的应用。
实验二：等差数列等差数列是指数列中的每个数与前一个数的差值都相等的数列。
我们选择了一个等差数列进行实验研究，通过观察数列的规律和特点，我们可以更好地理解等差数列的性质。
实验结果表明，等差数列具有明显的规律性。
首先，数列中的每个数与前一个数的差值都相等，这种规律使得数列中的数字之间有着稳定的关系。
其次，等差数列的增长速度是恒定的，数列中的数字呈现出线性增长的趋势。
这种特点在物理学、经济学等领域中有着重要的应用。
实验三：等比数列等比数列是指数列中的每个数与前一个数的比值都相等的数列。
我们选择了一个等比数列进行实验研究，通过观察数列的规律和特点，我们可以更好地理解等比数列的性质。
实验结果显示，等比数列也具有明显的规律性。
首先，数列中的每个数与前一个数的比值都相等，这种规律使得数列中的数字之间有着稳定的关系。
其次，等比数列的增长速度是不断加快或减慢的，数列中的数字呈现出指数增长或衰减的趋势。
这种特点在物理学、生物学等领域中有着广泛的应用。
实验四：素数序列素数序列是指仅能被1和自身整除的正整数序列。
我们选择了一个素数序列进行实验研究，通过观察数列的规律和特点，我们可以更好地理解素数的分布规律。
一、实验目的1. 理解数字逻辑的基本概念和原理。
2. 掌握逻辑门电路的基本功能和应用。
3. 学会使用逻辑门电路设计简单的组合逻辑电路。
4. 培养实际动手能力和分析问题、解决问题的能力。
二、实验原理数字逻辑是研究数字电路的基本原理和设计方法的一门学科。
数字电路是由逻辑门电路组成的，逻辑门电路是实现逻辑运算的基本单元。
常见的逻辑门电路有与门、或门、非门、异或门等。
组合逻辑电路是由逻辑门电路组成的，其输出仅与当前的输入有关，而与电路的历史状态无关。
组合逻辑电路的设计方法主要有真值表法、逻辑函数法、卡诺图法等。
三、实验仪器与设备1. 数字逻辑实验箱2. 移动电源3. 连接线4. 逻辑门电路模块5. 计算器四、实验内容1. 逻辑门电路测试（1）测试与门、或门、非门、异或门的功能。
（2）测试逻辑门电路的输出波形。
2. 组合逻辑电路设计（1）设计一个4位二进制加法器。
（2）设计一个4位二进制减法器。
（3）设计一个4位二进制乘法器。
（4）设计一个4位二进制除法器。
五、实验步骤1. 逻辑门电路测试（1）将实验箱上相应的逻辑门电路模块插入实验板。
（2）根据实验要求，连接输入端和输出端。
（3）打开移动电源，将输入端接入逻辑信号发生器。
（4）观察输出波形，记录实验结果。
2. 组合逻辑电路设计（1）根据实验要求，设计组合逻辑电路的原理图。
（2）根据原理图，将逻辑门电路模块插入实验板。
（3）连接输入端和输出端。
（4）打开移动电源，将输入端接入逻辑信号发生器。
（5）观察输出波形，记录实验结果。
六、实验结果与分析1. 逻辑门电路测试实验结果如下：（1）与门：当两个输入端都为高电平时，输出为高电平。
（2）或门：当两个输入端至少有一个为高电平时，输出为高电平。
（3）非门：输入端为高电平时，输出为低电平；输入端为低电平时，输出为高电平。
（4）异或门：当两个输入端不同时，输出为高电平。
2. 组合逻辑电路设计实验结果如下：（1）4位二进制加法器：能够实现两个4位二进制数的加法运算。
数字实验报告数字信号处理实验报告姓名：潘文才学号：08150227班级：0610802地点：YF303时间：第九、十、十一周星期三9-10节实验一：实验名称：时域采样定理一、实验目的：1. 学习掌握 matlab 的编程知识及其 matalab 在数字信号处理方面常用的12个函数2. 熟悉理想采样的性质，了解信号采样前后的频谱变化，加深对采样定理的理解。
二、实验内容：一、对给定的模拟信号Xa(t) =Ae-at sin(Ωt)U (t)进行采样！（fm=500）1，用鼠标双击电脑桌面的matlab6.5的快捷图标，运行matlab6.5主程序。
2,在matlab 命令窗口中输入，如下图示>>n = 0:50-1;>>fs = 1000;>>string = '1000';>>Xa=444.128*exp((-222.144)*n/fs).*sin(222.144*n/fs);>>DFT(Xa,50,string);3，如果输入的命令没有错误会出现如下绘图对话框。
从中大家可以再次体会函数DFT(x,N,str)的功能。
4，将实验图形导出，保存，选择Export 菜单项。
5，在导出对话框中选择文件格式为bmp，输入保存的文件名后，点击保存按钮。
这时保存的实验结果可以用WINDOWS自带的画图工具打开。
6，关闭matlab 的绘图对话框，在命令窗口中输入>>clear all；>>close all;>>clc;后，试将第三步中输入的 fs 改成 500Hz，或 1500Hz，画出采样后信号的波图和幅频特性曲线（如下图所示），并按第5步中的方法保存实验图形。
二、掌握 Matlab 基本的编程方法和基本的绘图函数。
1，用 Matlab 打开 C:\MATLAB6p5\work\chouyang.m 文件，（可按实验内容一，步骤11-12 的方法），该运行 M 文件后，绘制出模拟信号X(t)=1.5sin(2.5π )的波形，及其经过采样频率 fs= 4Hz 采样后，信号 X(nTs) ， X(n) 的波形。
2，运行 chouyang.m 文件。
3，在仔细阅读chouyang.m文件中的内容后，在掌握figure( )、 subplot( )、plot( )、title( )、stem( )函数的基础上编写 M 文件绘制模拟信号Xa (t) = 444.128e -222.144t sin(222.144t)U (t)波形，及其经过采样频率 fs= 1000Hz 采样后，信号 Xa(nTs)， Xa(n)的波形。
三、实验图形：四、思考题：1，观察实验内容 1 中，在分别采用 500Hz，1000Hz，1500Hz 采样后，对所得的到的信号 Xa(n)绘制的 3 个幅频特性曲线有何不同，并分析为什么？结合时域采样定理的内容对图形进行解释；答：在分别采用 500Hz，1000Hz，1500Hz 采样后，对所得的到的信号 Xa(n)绘制的 3 个幅频特性曲线分析可知：采样频率越大，其傅氏变换所得的图形的幅值变化越尖锐。
由时域采样定理知，当采样频率fs.max大于信号中，最高频率fmax的2倍时，即：fsmax>=2fmax,则采样之后的数字信号完整地保留了原始信号中的信息所得信号原形越完整地保留了原始信号中的信息，以保证可以从采样信号中无失真的恢复出原来的信号。
2，思考如何编写 Matlab M 文件，完成从 Xa(n)恢复出 Xa(t)的功能。
如果给定 Matlab函数 sinc(x)（sinc(x) = sin(πx)/πx），和 conv（a，b）函数完成矢量 a ，b 的卷积。
答：答：采样时在满足采样定理条件的情况下fs>=2fm,将Xa(jw)通过一个理想低通滤波器 ，利用它滤除高频成分，即可恢复原信号。
Ya(jw)=Xa(jw)H(jw),h(t)=⎰∞∞-dw jw H e jwt )(21π ya(t)=xa(t)*h(t)=∑∞-∞=--m a mT t TmT t T mT x )()](sin[)(ππ,有给定的matlab 函数sinc(x)及conv(a,b)恢复出xa （t ）。
实验二：实验名称： 时域离散系统及其响应一、实验目的：1. 继续熟悉掌握 matlab 的使用和编程2. 熟悉掌握时域离散系统的时域特性。
3. 验证时域卷积定理。
二、实验内容：1. 给定系统h1(n)=δ(n) +2.5δ (n−1) +2.5δ (n− 2) + δ(n −3) ，输入信号为x1 (n) =δ(n)， 用matlab 画出输入、系统和输出y1(n)在时域和频域的图形（提示可以调用 conv 和DFT(x,N,str)函数， 每次调用DFT(x,N,str)函数前先调用figure 函数） 。
在matlab 中可以对一矢量（矩阵）赋初值，除了像“实验一”中可以用冒号操作符外还可以下面的方法，比如我们定义矢量 h1 来表示h1(n)，可以用 h1 = [ 1, 2.5, 2,5 ,1]; h1的长度可由length 函数求得。
保存三幅实验结果图形2. 给定系统h2 (n) =R10 (n) ，输入信号为x 2(n) = R 10 (n) ，用 matlab 画出输入、系统和输出y 2 (n)在时域和频域的图形。
保存三张实验结果图形。
3. 给定系统h3 (n) = R10 (n )、，输入信号为x3(t) =R5 (n ) ，用matlab画出输入、系统和输出y3(n) 在时域和频域的图形。
并将FT [y3(n)] 与X3 [exp*(jw )] •H 3 [exp *(jw)] 进行比较，我们先只是比较︱FT [y3(n)]︱与︱X 3[ exp*(jw)]︱•︱H3[exp* ( jw)]︱是否一样，验证时域卷积定理。
DFT(x,N,str)函数定义为function [c,l]=DFT(x,N,str)，调用DFT函数后返回两个值，c 为给定的数字信号x 的X 3 [exp* (jw)]的值，当ω=[−4π,−3.99π,−3.98π,−3.97π …0.02π ,-0.01π,0,-0.01π,0.02π,3,97π ,3.98π ,3.99π ,4π]，1的值为l=[−4π,−3.99π ,−3.98π,−3.97π…0.02π,-0.01π,0,-0.01π,0.02π,3,97π ,3.98π ,3.99π ,4π]试编写M 文件完成步骤3，保存如下四张实验结果图形,并保存M 文件（在编写文件过程中注意matlab中“*”和“.*”操作符的区别.)三、实验图形：四、思考题：1．比较y1(n)和h1(n)的时域和频域特性，注意它们之间有无差别，用所学理论解释所得结果。
判断y 2 (n) 图形及其非零序列长度是否与理论结果一致，说出一种判断y (n) 图形正确与否的方法。
答： y1和h1的时域和频域特性的波形是一致的。
H1是长度为 4的有限长序列，而频域采样的点数为9大于4点，所以可以有其主值序列不失真的恢复出原始信号。
y2图形及其非零序列长度与理论结果一致。
2. matlab 的工具箱函数conv，能用于计算两个有限长序列之间的卷积，但conv 函数假定这两个序列都从n=0开始。
试编写M文件计算x (n)=[3,11,7, 0, −1, 4, 2], −3 ≤n≤3和h (n) = [2,3,0, −5,2,1], −1≤n≤4之间的卷积，并绘制y (n)的波形图。
答：程序：nx=[-3,-2,-1,0,1,2,3]; x =[3,11,7,0,-1,4,2];nh=[-1,0,1,2,3,4];h=[2,3,0,-5,2,1];nyb=nx(1)+nh(1); nye=nx(length(x))+nh(length(h)); y=conv(x,h);figure;s tem(ny,y,’.’);实验三：实验名称：用FFT 进行谱分析一、实验目的1.进一步加深对DFT算法原理和基本性质的理解2.熟悉FFT算法原理和FFT子程序的应用。
3.学习用FFT 对连续信号和时域离散信号进行谱分析的方法，了解可能出现的分析误差及其原因，以便在实际中正确应用FFT。
二．实验原理1．快速傅立叶变换(FFT)算法：长度为N的序列的离散傅立叶变换为N点的DFT 可以分解为两个N/2点的DFT，每个N/2点的DFT又可以分解为两个N/4点的DFT。
依此类推，当N为2的整数次幂时，由于每分解一次降低一阶幂次，所以通过M次的分解，最后全部成为一系列2点DFT运算。
2．利用FFT进行频谱分析：若信号本身是有限长的序列，计算序列的频谱就是直接对序列进行FFT运算求得，就代表了序列在幅度谱和相位谱之间的频谱值。
若信号是模拟信号，用FFT进行谱分析时，首先必须对信号进行采样，使之变成离散信号，然后就可按照前面的方法用FFT来对连续信号进行谱分析。
三、实验步骤1.复习DFT 的定义、性质和用DFT 作谱分析的有关内容。
2.复习FFT算法原理与编程思想，并对照DIT-FFT运算流图和程序框图，读懂本实验提供的FFT子程序。
3.编制信号产生子程序，产生以下典型信号供谱分析用：x1(n )= R4（n）（1-1）x2(n )=[1,2，3，4，4，3，2，1]（1-2）x 3(n) = [4，3，2，1，1，2，3，4]（1-3）x4(n) = cos(π/4 *n ) （1-4）x5 (n ) = sin(π/8* n) （1-5）x6 (t ) = cos(8πt) + cos(16πt) + cos(20πt) （1-6）4.编写M文件。
5.按实验内容要求，上机实验，并写出实验报告。
四、实验内容主要使用的MATLAB 函数：函数fft(x)可以计算R 点序列的R 点DFT值；而fft(x,N)则计算R 点序列的N 点DFT，若R>N，则直接截取R 点DFT的前N 点，若R<N，则x先进行补零扩展为N 点序列再求N 点DFT。
1、编写matlabM文件对信号x1 (n)做8点和16点的FFT，保存实验结果图形。
2、编写matlabM文件对信号x2( n )做8点和16点的FFT，保存实验结果图形。
3、编写matlabM文件对信号x4 (n )做8点和16点的FFT，保存实验结果图形。
4、编写matlab M文件对信号x6 (t )以fs=64（Hz）采样后做N=16、32、64点的FFT，保存三幅实验结果图形。
五、结果图形六、思考题1.在N=8 和N=16 两种情况下，x2 (n)、x3 (n)的幅频特性会相同吗？为什么？答：N=8时x2 (n)、x3 (n)的幅频特性是相同的，而N=16时x2 (n)、x3 (n)的幅频特性是不相同的。
