2011-2012学年度浙江省金华一中高三年级第二次月考

学必求其心得，业必贵于专精金华一中2011——2012学年高三十月月考物理试卷一．单项选择题（每小题只有一个选项正确，每小题3分，共21分）1.如图是描述一球从水平桌面上方一点自由下落（空气阻力不计)，与桌面经多次碰撞最后静止在桌面上的运动过程，则图线上y 轴所反映的是下列哪个物理量随时间的变化过程( ） A ．位移 B ．路程 C ．速度 D ．加速度 2。

如图,轻弹簧上端固定，下端挂质量为m 1的吊篮，吊篮中放质量为m 2的物体，吊篮下面悬挂质量为m 3的物体。

剪断悬挂m 3细绳后的极短时间,m 2对吊篮底部的压力是( ） A ．ｍ２ｇ B ．m 2m 3g ／（m 1+m 2） C ．m 2（m 1+m 2+m 3）ｇ／(ｍ１+ｍ２） D ．m 2（m １+m 3)ｇ／ｍ１ 3.石块A 自塔顶自由下落ｈ1时,石块B 从离塔顶ｈ2处自由下落，后来两石块同时到达地面，由此可知此塔高为( ） A ．ｈ1＋ｈ2 B ．（h 1+h 2）2／4h 1 C ．h 12／（h 1+h 2) D ．（h 1+h 2）2／（h 1—h 2) 4。

某同学在篮球训练中，以一定的初速度投篮，篮球水平击中篮板，现在他向前走一小段距离，与篮板更近，再次投篮，出手高度和第一次相同，篮球又恰好水平击中篮板上的同一点，则（ ) A ．第二次投篮篮球的初速度大些 B ．第二次击中篮板时篮球的速度大些 C ．第二次投篮时篮球初速度与水平方向的夹角大些 D ．第二次投篮时篮球在空中飞行时间长些5。

如图所示,质量m =1kg 、可看成质点的小物块静止在水平桌面上, 且与桌子边缘相距0。

4m,物块与桌面间的动摩擦因数为 =0.4.现用F =5N 的水平力向右推小物块，为了使它从桌子上掉下，则力F 的作用时间至少为( ）A ．0．8sB ．1。

0s Ｃ．255s D ．2105s 6。

物块从光滑曲面的P 点由静止下滑，通过粗糙的静止水平传送带后落到了地面上的Q 点，现使传送带开始匀速转动，再把物块由P 点静止释放，则有关下列说法正确的是( ) A ．若传送带逆时针转动，物块落到Q 点左侧 B ．若传送带顺时针转动，物块落到Q 点右侧m 1 m 2 m 3学必求其心得，业必贵于专精C．若传送带顺时针转动，物块落到Q点D．无论传送带转动方向如何，物块不可能落到Q点左侧7。

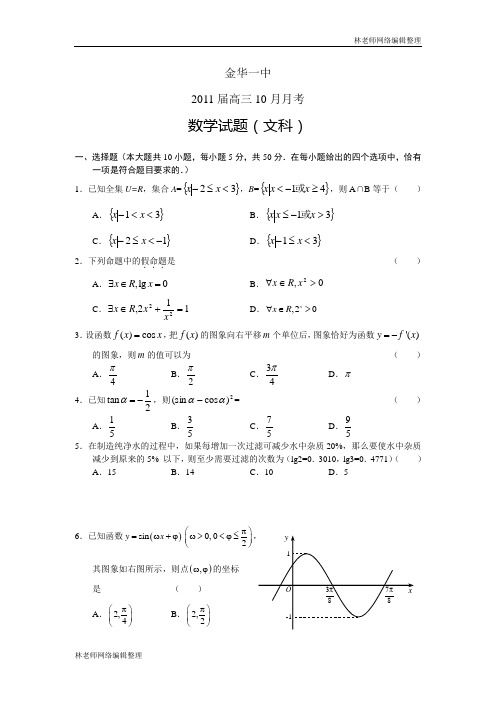
yxO38π 78π 1-1金华一中 2011届高三10月月考数学试题（文科）一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，恰有一项是符合题目要求的．） 1．已知全集U=R ，集合A =}{32<≤-x x ，B ={}41≥-<x x x 或，则A ∩B 等于（ ） A ．{}31<<-x x B ．{}31>-≤x x x 或C ．{}12-<≤-x xD ．{}31<≤-x x 2．下列命题中的假命题．．．是（ ）A ．,lg 0x R x ∃∈=B ．0,2>∈∀x R xC ．112,22=+∈∃xx R x D ．,20x x R ∀∈>3．设函数()cos f x x =，把()f x 的图象向右平移m 个单位后，图象恰好为函数'()y f x =-的图象，则m 的值可以为（ ）A ．4π B ．2πC ．34πD ．π 4．已知1tan 2α=-，则2)cos (sin αα-=（ ） A ．51 B ．53 C ．57D ．595．在制造纯净水的过程中，如果每增加一次过滤可减少水中杂质20%，那么要使水中杂质减少到原来的5% 以下，则至少需要过滤的次数为（lg2=0．3010，lg3=0．4771）（ ） A ．15 B ．14 C ．10 D ．56．已知函数()sin y x =ω+ϕ0,02π⎛⎫ω><ϕ≤ ⎪⎝⎭，其图象如右图所示，则点(),ωϕ的坐标 是（ ）A ．2,4π⎛⎫⎪⎝⎭B ．2,2π⎛⎫ ⎪⎝⎭C ．4,4π⎛⎫ ⎪⎝⎭D ．4,2π⎛⎫ ⎪⎝⎭7．已知函数22()2,()log ,()log 2xf x xg x x xh x x =+=+=-的零点依次为,,a b c ，则（ ） A ．a b c << B ．c b a << C ．c a b << D ．b a c <<8．设==)21(,2cos )(sin f x x f 则（ ）A ．-21B ．-23 C ．21D ．23 9．已知数列{}n a 满足221221,2,(1cos )sin 22n n n n a a a a ππ+===++，则该数列的前20项的和为（ ）A ．2010B ．2056C ．2065D ．210110．若x x x f λ+=2)(（x ∈N*）是单调增函数，则实数λ的取值范围是 （ ）A ．2->λB ．3->λC ．2-≥λD ．3-≥λ二、填空题（本大题共7小题，每小题4分，共28分．） 11．函数1lg y x x =-+的定义域为 ； 12．已知3(,0),sin ,25παα∈-=-则=-)4cos(πα ；13．已知直线a x y -=与曲线x y ln =相切，则a 的值为 ； 14．若关于x 的方程01=+k x在]1,0(∈x 有实数根，则k 的取值范围为 ； 15．已知整数以按如下规律排成一列：()1,1、()1,2、()2,1、()1,3、()2,2，()3,1，()1,4，()2,3，()3,2，()4,1，……，则第60个数对是 ；16．对函数()sin f x x x =，现有下列命题：①函数()f x 是偶函数,②函数()f x 的最小正周期是2π,③函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递增，在区间,02π⎡⎤-⎢⎥⎣⎦上单调递减．其中是真命题的是 （写出所有真命题的序号）；17．已知不等式022<+-a x x 的整数解只有1，则实数a 的取值范围是 ． 三、解答题（本大题共5小题共72分．解答时应写出文字说明、证明过程或演算步骤．） 18．（本题满分12分）已知函数2()sin cos2x f x x a =+，a 为常数，a R ∈，且2π=x 是方程0)(=x f 的解（1）求)611(πf 的值； （2）当],0[π∈x 时，求函数)(x f 的值域．19．（本题满分14分）已知等差数列}{n a 中，43=a ，其前10项和为65 （1）求数列}{n a 的通项公式； （2）求数列}2{n na 的前n 项和n S ．20．（本题满分15分）已知数列{}n a 中，11=a ，12nn n a a ++=（n ∈N*），n n a b 3=（1）试证数列⎭⎬⎫⎩⎨⎧⨯-n n a 231是等比数列，并求数列{n b }的通项公式； （2）在数列{n b }中，是否存在连续三项成等差数列的项，若存在，求出所有这样的项，若不存在，说明理由．21．（本题满分15分）已知函数x ax x x f 54)(23+-=（R ∈a ）． （1） 当a = 1时, 求函数在区间[0, 2]上的最大值;（2） 若函数)(x f 在区间[0, 2]上无极值．．．, 求a 的取值范围．22．（本题满分16分）已知函数x a x x f ln 2)(2-=（0a >）． （1）讨论函数()f x 的单调性；（2）若关于x 的方程()2f x ax =有唯一解，求a 的值．参考答案一、选择题（每小题5分，共50分） 题号 1 2 3 4 5 6 7 8 9 10 答案CBBDBAACDB二、填空题（每小题4分，共28分） 11．(0,1] 12．10213．1 14．1-≤k 15．()5,7 16．①，③ 17．10<≤a 三、解答题（共72分）18．（本题满分12分）已知函数2()sin cos2x f x x a =+，a 为常数，a R ∈，且2π=x 是方程0)(=x f 的解． （1）求)611(πf 的值; （2）当],0[π∈x 时，求函数)(x f 的值域． 解：（1）2()sincos 0224f a πππ=+=，则1102a +=，解得2a =-……………2分所以2()sin 2cossin cos 12xf x x x x =-=--…………………………………4分 所以233)611(-=πf ．……………………………………………………………6分（2）()2sin()14f x x π=--……………………………………………………8分由[0,]x π∈，得 3[,]444x πππ-∈-，则2sin()[,1]42x π-∈-……………10分则2sin()14x π--∈[2,21]--所以()y f x =值域为[2,21]-- ………12分19．（本题满分14分）已知等差数列}{n a 中，43=a ，其前10项和为65 （1）求数列}{n a 的通项公式; （2）求数列}2{n na 的前n 项和n S ． 解：（1） 421=+d a ，652910101=⨯+d a ……………………4分得121==d a ， 1+=∴n a n …………………………………………………6分（2）2323412222n n n S +=++++L ① 23113412222n n n S ++=+++L ②①—②得23411111111222222n n n n S ++=+++++-L ………………………………10分1121211)211(411++----+=n n n 1121)211(211+----+=n n n332n n n S +∴=-……………………………………………………14分20．（本题满分15分）已知数列{}n a 中，11=a ，12nn n a a ++=（n ∈N*），b n ＝3a n（1）试证数列⎭⎬⎫⎩⎨⎧⨯-n n a 231是等比数列，并求数列{b n }的通项公式；（2）在数列{b n }中，是否存在连续三项成等差数列的项，若存在，求出所有这样的项，若不存在，说明理由．解：（1）证明: 由12nn n a a ++=，得a n ＋1＝2n —a n ，∴nn n n nn n n n a a a a 2312312231231111⨯-⨯--=⨯-⨯-+++1231231-=⨯-⎪⎭⎫ ⎝⎛⨯--=n n n n a a ,∴数列⎭⎬⎫⎩⎨⎧⨯-n n a 231是首项为31321=-a ,公比为1-的等比数列．………………4分∴ ()1131231--⨯=⨯-n n n a , 即()[]nn n a 1231--=，∴()21nn n b =--………………………………………………………………………7分（2）解：假设在数列{b n }中，存在连续三项b k －1，b k ，b k ＋1（k ∈N*, k ≥2）成等差数列，则b k －1＋b k ＋1＝2b k ，即()()()1111[21][21]2[21]k k kk k k -+-+--+--=--，即12k -＝41(1)k --……………………………………………………………10分若k 为偶数，则12k -＞0，41(1)k --＝－4＜0，所以，不存在偶数k ，使得b k －1，b k ，b k ＋1成等差数列。

金华一中2011—2012学年高三第二次月考化学试卷相对原子质量：H:1 C:12 N:14 Na:23 O:16 Mg:24 Cl: 35.5 Mn:55 K:39 一、选择题（每小题只有一个正确选项，1~10题每题2分，11~20题每题3分，共50分）1．分类法在化学的发展中起到非常重要的作用,下列分类标准合理的是①根据氧化物的组成元素将氧化物分成酸性氧化物、碱性氧化物和两性氧化物②根据反应中是否有电子转移将化学反应分为氧化还原反应和非氧化还原反应③根据分散系是否有丁达尔效应将分散系分为溶液胶体和浊液④根据反应中的热效应将化学反应分为放热和吸热反应⑤根据水溶液能否导电将化合物分为电解质和非电解质A．②④B．②③④C．①③⑤D．①②④⑤2．下列叙述正确的是A．1.00mol NaCl中含有6.02×1023个NaCl分子B．1.00mol NaCl中,所有Na+的最外层电子总数为8×6.02×1023C．欲配置1.00L ,1.00mol.L-1的NaCl溶液，可将58.5g NaCl溶于1.00L水中D．1molCl2与足量的铁反应，转移的电子数为3N A[来3．下列溶液中Cl-浓度与50 mL 1 mol·L-1 AlCl3溶液中Cl-浓度相等的是A．150 mL 1 mol·L-1的NaCl溶液 B．75 mL 2 mol·L-1 NH4Cl溶液C．25 mL 1.5 mol·L-1的MgCl2溶液 D．25 mL 2 mol·L-1的FeCl3溶液4．某溶液中含有HCO3－、CO32－、SO32－、Na+、NO3－五种离子。

若向其中加入Na2O2粉末，充分反应后（溶液体积变化忽略不计），溶液中离子浓度保持不变．．的是A．NO3－B．CO32－、NO3－C．SO32－、NO3－D．CO32－、NO3－、Na+5．氧化还原反应中，水的作用可以是氧化剂、还原剂、既是氧化剂又是还原剂、既非氧化剂又非还原剂等。

金华一中2011—2012学年高三第二次月考高三历史2011.10一．选择题：满分51分。

本大题共34小题，每小题1.5分。

在每小题列出的四个选项中，只有一项符合题目要求。

1．《荀子·儒效篇》记载：“（周公）兼制天下，立七十一国，姬姓独居五十三人。

”可见同姓亲族是西周分封的主体。

这些同姓亲族受封时，周王会给予他们A．封号和耕牛 B．土地和耕牛 C．土地和人口 D．人口和铁犁2．《史记·楚世家》载：“楚之先祖出自帝颛顼高阳。

……(楚庄王)八年，伐陆浑戎，遂至洛，观兵于周郊。

……庄王曰：“子无阻九鼎；楚国折钩之喙，足以为九鼎。

”上述材料反映的历史信息有：①楚国国君是先代贵族的后代②楚国拥有自己的军队③楚王有随从周天子作战的义务④周王室已经衰弱A．①② B．②④ C．①③④ D．①②③④3．“齐人”、“鲁人”、“楚人”这种表述，逐渐让位于以行政区划为籍贯的表述，造成这一变化的制度因素是A．分封制 B．宗法制 C．郡县制 D．三省六部制4．刘邦在位末年与众臣歃血为盟，特别诏令：“非刘氏而王者，若无功，上所不置而侯者，天下共诛之。

”其目的在于A．加强朝廷对地方的控制 B．禁止分封异姓王侯C．鼓励群臣建立军功 D．安抚汉初以来的功臣5．“宰相之职，佐天子总百官，治万事，其任重矣。

”以下被称为宰相的各朝官职中，其职权与引文所述的官职相符的是A．秦御史大夫B．唐尚书令 C．明内阁首辅D．清军机大臣6．右侧是18世纪一位法国贵族肖恩公爵“最重要的中国藏品”目录，从中可以推测A．当时的清政府鼓励海外贸易 B．中国已陷入落后挨打的局面C．其收藏受到中国文化热影响 D．其藏品都是从中国掠夺而来7．“海东龙泣舰沉波，上相锚轩(古代使臣乘坐的一种轻车)出议和……台人号泣秦桧歌，九城谣谍遍网罗。

”从该诗中可以获取的有效历史信息有①甲午海战战斗壮烈②清政府被迫签定《马关条约》③台湾人民的反割台斗争遭到清廷压制④维新派发起挽救民族危亡的斗争A．①②③ B．①③④ C．②③④ D．①②③④8．义和团反洋教斗争反映了A．中国农民与西方文明的冲突B．中国人民与清朝政府矛盾的激化C．中国文化与列强的矛盾的激化D．中国与西方列强的矛盾的激化9．有人说洪秀全和曾国藩的斗争是“耶稣与孔子的斗争”。

金华市高一年上学期语文第二次月考（12月）试卷姓名:________ 班级:________ 成绩:________一、新添加的题型 (共2题；共10分)1. （5分） (2017高一下·惠来期末) 补写出下列句子中的空缺部分。

（1）《氓》是一首叙事诗，诗中写男主人公“言既遂矣，至于暴矣”，诗歌前文对男主人公变化埋下伏笔的句子是：“________，________。

”（2）白居易《琵琶行》中穿插的景物描写很好地起到了渲染感情的作用。

如“________”一句借秋江冷月抒写琵琶女的孤单与寂寞，画龙点睛。

（3）韩愈在《师说》中以“________，________”两句强调“道”与“师”同在，从师是为了学道。

2. （5分）(2020·江苏模拟) 阅读下面的材料，按要求作文。

两个中学生看全运会乒乓球比赛，世界排名第一的丁宁和一位名气不大的选手正打得难分难解。

甲说：“这位选手真倒霉，碰上国手，赢的希望很渺茫。

”乙说：“这位选手真幸运，遇上了世界第一。

”读了这则材料，你有怎样的感悟或联想？请根据自己感悟或联想写一篇不少于800字的作文。

你可以讲述故事，抒发情感，也可以发表见解。

二、选择题 (共5题；共14分)3. （2分）下列划线字的读音全都相同的一组是（）。

A . 喧嚣渲染寒暄喧宾夺主B . 涨潮膨胀账单怅然若失C . 严峻疏浚竣工逡巡不前D . 聒噪干燥暴躁名噪一时4. （2分）下列各句中，加横线成语使用不恰当的一项是（）A . 世上举案齐眉的夫妻一定是有的，不能以我等瓢勺相碰的日子，揣测人家的和睦是虚伪。

B . 如不抓住时机，及时见报，这则消息将成为陈词滥调。

C . 苏杭山水果然名不虚传、秀色可餐，称之为“人间天堂”实不为过。

D . 张家辉近来在杜其峰的作品中频频亮相，展露了自己的表演才华，尤其在《黑社会》系列中的表演更是可圈可点。

5. （2分） (2017高一下·潮南月考) 下列各句中，没有语病的一句是（）A . 岁月留声不留人，歌曲《敢问路在何方》在猴年春节又经历了一轮传唱，这首歌的词作者——著名艺术家、空军政治部文工团创作员阎肃却悄然离世。

2011-2012学年浙江省金华市某校高三（下）第二次统练数学试卷（文科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知全集U =R ，集合A ={x|x +1<0}，B ={x|x −3<0}，那么集合(∁U A)∩B =( )A {x|−1≤x <3}B {x|−1<x <3}C {x|x <−1}D {x|x >3} 2. 已知x ，y 满足约束条件{y ≤xx +y ≤1y ≥−1 ，则z ＝2x +y 的最大值为（ ）A 3B −3C 1D 323. 设x ，y 是两个实数，则“x ，y 中至少有一个数大于1”是“x 2+y 2>2”成立的（ ） A 充分非必要条件 B 必要非充分条件 C 充分必要条件 D 既非充分又非必要条件4. 等差数列{a n }中，a 3+a 5+a 7+a 9+a 11=20，则a 8−12a 9=( )A 1B 2C 3D 45. 如果若干个函数的图象经过平移后能够重合，则称这些函数“互为生成”函数，给出下列函数：①f(x)=sinx −cosx ，②f(x)=√2(sinx +cosx)， ③f(x)=√2sinx +2，④f(x)=sinx ，其中互为生成的函数是（ ） A ①② B ①③ C ③④ D ②④6. 已知直线l ⊥平面α，直线m // 平面β，下列命题中正确的是（ ）A α⊥β⇒l ⊥mB α⊥β⇒l // mC l ⊥m ⇒α // βD l // m ⇒α⊥β 7. △ABC 内接于以O 为圆心，1为半径的圆，且3OA →+4OB →+5OC →=0→，则OC →⋅AB →的值为（ ）A −15B 15C −65D 658. 定义域为R 的函数f(x)对任意x ∈R 都有f(x)=f(4−x)，且其导函数f′(x)满足(x −2)f′(x)>0，则当2<a <4时，有（ ）A f(2a )<f(2)<f(log 2a)B f(2)<f(2a )<f(log 2a)C f(2)<f(log 2a)<f(2a )D f(log 2a)<f(2a )<f(2) 9. 设复数ω=−12+√32i ，则下列各式错误的是（ ）A ω3=1B ω2+ω=−1C ω2−ω=−1D ω2−ω是纯虚数10. 设双曲线C:x 2a 2−y 2b 2=1(b >a >0)的左、右焦点分别为F 1，F 2．若在双曲线的右支上存在一点P ，使得|PF 1|＝3|PF 2|，则双曲线C 的离心率e 的取值范围为（ ） A (1, 2] B (√2,2] C (√2,2) D (1, 2)二、填空题：本大题共7小题，每小题4分，共28分．11. 设函数f(x)=ln(ax2+1)．若f(x)=lnax有唯一的零点x0(x0∈R)，则实数a=________．12. 若存在直线l平行于直线3x−ky+6=0，且与直线kx+y+1=0垂直，则实数k=________．13. 假设一个四棱锥的正视图和侧视图为两个完全相同的等腰直角三角形（如图所示），腰长为1，则该四棱锥的体积为________．14. a n=6n−4(n=1, 2, 3, 4, 5, 6)构成集合A，b n=2n−1(n=1, 2, 3, 4, 5, 6)构成集合B，任取x∈A∪B，则x∈A∩B的概率是________．15. 已知sinα+cosα=713，0<α<π，则tanα=________．16. 设椭圆C:x225+y29=1，F是右焦点，l是过点F的一条直线（不与y轴平行），交椭圆于A、B两点，l′是AB的中垂线，交椭圆的长轴于一点D，则DFAB的值是________．17. 若不等式x+2√xy≤a(x+y)对任意的实数x>0，y>0恒成立，则实数a的最小值为________．三、解答题：本大题共5小题，共72分，解答应写出文字说明、证明过程或演算步骤．18. 已知向量a→=(12,12sinx+√32cosx)与b→=(1,y)共线，设函数y=f(x)．（1）求函数f(x)的周期及最大值；（2）已知锐角△ABC中的三个内角分别为A、B、C，若有f(A−π3)=√3，边BC=√7，sinB=√217，求△ABC的面积．19. 如图，AC是圆O的直径，点B在圆O上，∠BAC=30∘，BM⊥AC交AC于点M，EA⊥平面ABC，FC // EA，AC=4，EA=3，FC=1．（1）证明：EM⊥BF；（2）求平面BEF与平面ABC所成的锐二面角的余弦值．20. 数列{a n}满足a n+1+a n=4n−3(n∈N∗)(I)若{a n}是等差数列，求其通项公式；(II)若{a n}满足a1=2，S n为{a n}的前n项和，求S2n+1．21. 设椭圆C:x 2a 2+y 2b 2=1(a >b >0)的一个顶点与抛物线C:x 2=4√3y 的焦点重合，F 1，F 2分别是椭圆的左、右焦点，且离心率e =12且过椭圆右焦点F 2的直线l 与椭圆C 交于M 、N 两点．（1）求椭圆C 的方程；（2）是否存在直线l ，使得OM →⋅ON →=−2．若存在，求出直线l 的方程；若不存在，说明理由．（3）若AB 是椭圆C 经过原点O 的弦，MN // AB ，求证：|AB|2|MN|为定值． 22. 设x 1、x 2(x 1≠x 2)是函数f(x)=ax 3+bx 2−a 2x(a >0)的两个极值点． （1）若x 1=−1，x 2=2，求函数f(x)的解析式；（2）若 |x 1|+|x 2|=2√2，求b 的最大值；（3）设函数g(x)=f′(x)−a(x −x 1)，x ∈(x 1, x 2)，当x 2=a 时，求|g(x)|的最大值．2011-2012学年浙江省金华市某校高三（下）第二次统练数学试卷（文科）答案1. A2. A3. D4. B5. B6. D7. A8. C9. C 10. B 11. 4 12. 0 13. √23 14. 13 15. −125 16. 25 17.√5+1218. 解：（1）∵ 向量a →=(12,12sinx +√32cosx)与 b →=(1,y)共线∴ 12y=12sinx+√32cosx∴ y=f(x)=2sin(x+π3)∴ 函数f(x)的周期T=2π当x=2kπ+π6，k∈Z时，函数f(x)的最大值为2；（2）∵ f(A−π3)=√3∴ 2sin(A−π3+π3)=√3∴ sinA=√32∵ 0<A<π2∴ A=π3∵ BC=√7，sinB=√217，∴ √7sinπ3=√217∴ AC=2∵ sinC=sin(π−A−B)=sin(A+B)=sinAcosB+cosAsinB=√32×2√77+12×√217=3√2114∴ △ABC的面积S=12×2×√7×3√2114=3√32．19. 解：（1）证明：∵ EA⊥平面ABC，BM⊂平面ABC，∴ EA⊥BM．又∵ BM⊥AC，EA∩AC=A，∴ BM⊥平面ACFE，而EM⊂平面ACFE，∴ BM⊥EM．∵ AC是圆O的直径，∴ ∠ABC=90∘．又∵ ∠BAC=30∘，AC=4，∴ AB=2√3，BC=2，AM=3，CM=1．∵ EA⊥平面ABC，FC // EA，FCEA =13∴ FC⊥平面ABC．∴ △EAM与△FCM都是等腰直角三角形．∴ ∠EMA=∠FMC=45∘．∴ ∠EMF=90∘，即EM⊥MF（也可由勾股定理证得）．∵ MF∩BM=M，∴ EM⊥平面MBF．而BF⊂平面MBF，∴ EM⊥BF．（2）延长EF 交AC 于G ，连BG ，过C 作CH ⊥BG ，连接FH ．由（1）知FC ⊥平面ABC ，BG ⊂平面ABC ，∴ FC ⊥BG ．而FC ∩CH =C ，∴ BG ⊥平面FCH ．∵ FH ⊂平面FCH ，∴ FH ⊥BG ，∴ ∠FHC 为平面BEF 与平面ABC 所成的 二面角的平面角．在Rt △ABC 中，∵ ∠BAC =30∘，AC =4， ∴ BM =AB ⋅sin30∘=√3， 由FCEA =GCGA =13，得GC =2． ∵ BG =√BM 2+MG 2=2√3，又∵ △GCH ∽△GBM ，∴ GCBG =CHBM ，则CH =GC⋅BM BG=√32√3=1．∴ △FCH 是等腰直角三角形，∠FHC =45∘，∴ 平面BEF 与平面ABC 所成的锐二面角的余弦值为√22． 20. 解：( I)由题意得a n+1+a n =4n −3…① a n+2+a n+1=4n +1…②．… ②-①得a n+2−a n =4，∵ {a n }是等差数列，设公差为d ，∴ d =2， ∵ a 1+a 2=1∴ a 1+a 1+d =1，∴ a 1=−12．∴ a n =2n −52．(II)∵ a 1=2，a 1+a 2=1， ∴ a 2=−1．又∵ a n+2−a n =4，∴ 数列的奇数项与偶数项分别成等差数列，公差均为4， S 2n+1=(a 1+a 3+...+a 2n+1)+(a 2+a 4+...+a 2n ) =(n +1)×2+(n +1)n 2×4+n ×(−1)+n(n −1)2×4 =4n 2+n +2． 21. （1）解：抛物线C ：x 2=4√3y 的焦点为(0,√3) ∵ 椭圆C ：x 2a2+y 2b 2=1(a >b >0)的一个顶点与抛物线C ：x 2=4√3y 的焦点重合∴ 椭圆的一个顶点为(0,√3)，即b =√3 ∵ e =ca =√1−b 2a 2=12，∴ a =2， ∴ 椭圆的标准方程为x 24+y 23=1（2）解：由题可知，椭圆的右焦点为(1, 0)，直线l 与椭圆必相交．①当直线斜率不存在时，M(1, 32)，N(1, −32)，∴ OM →⋅ON →=(1,32)⋅(1,−32)=1−94=−54，不合题意．②设存在直线l 为y =k(x −1)(k ≠0)，且M(x 1, y 1)，N(x 2, y 2)．由{x 24+y 23=1y =k(x −1)得(3+4k 2)x 2−8k 2x +4k 2−12=0， x 1+x 2=8k 23+4k 2，x 1⋅x 2=4k 2−123+4k 2，OM →⋅ON →=x 1x 2+y 1y 2=x 1x 2+k 2[x 1x 2−(x 1+x 2)+1] =4k 2−123+4k 2+k 2(4k 2−123+4k 2−8k 23+4k 2+1)=−5k 2−123+4k 2=−2 所以k =±√2，故直线l 的方程为y =√2(x −1)或y =−√2(x −1)（3）证明：设M(x 1, y 1)，N(x 2, y 2)，A(x 3, y 3)，B(x 4, y 4)由（2）可得：|MN|=√1+k 2|x 1−x 2|=√(1+k 2)[(x 1+x 2)2−4x 1x 2] =√(1+k 2)[(8k 23+4k 2)2−4(4k 2−123+4k 2)]=12(k 2+1)3+4k 2．由{x 24+y 23=1y =kx消去y ，并整理得：x 2=123+4k 2，|AB|=√1+k 2|x 3−x 4|=4√3(1+k 2)3+4k 2，∴|AB|2|MN|=48(1+k 2)3+4k 212(k 2+1)3+4k 2=4为定值22. 解：（1）∵ f(x)=ax 3+bx 2−a 2x(a >0)， ∴ f′(x)=3ax 2+2bx −a 2(a >0)，依题意又−1和2是方程3ax 2+2bx −a 2=0的两根， ∴ {1=−2b3a−2=−a 3，解得{a =6b =−9，∴ f(x)=6x 3−9x 2−36x （经检验，适合）…3′（2）∵ f′(x)=3ax 2+2bx −a 2(a >0)，依题意，x 1、x 2是方程f′(x)=0的两个根， ∵ x 1x 2=−a3<0且|x 1|+|x 2|=2√2， ∴ (x 1−x 2)2=8． ∴ (−2b 3a)2+4a 3=8，∴ b 2=3a 2(6−a)， ∵ b 2≥0， ∴ 0<a ≤6．设p(a)=3a 2(6−a)，则p′(a)=−9a 2+36a ． 由p′(a)>0得0<a <4，由p′(a)<0得a >4，即p(a)在区间(0, 4]上是增函数，在区间[4, 6]上是减函数， ∴ 当a =4时p(a)有极大值96． ∴ p(a)在(0, 6]上的最大值是96，∴ b 的最大值为4√6．-----（3）∵ x 1、x 2是方程f′(x)=0的两个根， ∴ f′(x)=3a(x −x 1)(x −x 2)． ∵ x 1x 2=−a3，x 2=a ，∴ x 1=−13．∴ |g(x)|=|3a(x +13)(x −a)−a(x +13)|=|a(x +13)[3(x −a)−1]|，∵ x 1<x <x 2，即−13<x <a ， ∴ |g(x)|=a(x +13)(−3x +3a +1)=−3a(x +13)(x −3a +13)=−3a(x −a 2)2+3a 34+a 2+13a≤3a 34+a 2+13a=a(3a+2)212．|g(x)|max =a(3a+2)212，当且仅当x =a2时取“=”…15′。

金华一中高三地理10月考试题一．单项选择题。

（25小题，每小题2分共50分）2009年7月22日我国将出现罕见的日全食天象，日、月、地三者位于同一直线，月 影刚好投影在地球表面，并且自西向东扫过我国的长江流域，形成日全食观察带（如下图）。

届时位于月影区的人们能够观测到日全食。

读图回答1～2题1．月影带自东向西移动的原因是A.地球自西向东自转B.地球自西向东公转C.月球自西向东自转D.月球自西向东公转 2．成都与重庆日全食的相关描述正确的是A.成都开始晚、持续时间长B.成都开始早、持续时间短C.重庆结束早、持续时间长D.重庆结束晚、持续时间短 下图中a 、b 为太阳高度日变化曲线。

回答3～5题 3．若m 为北京时间8:40，且a 、b 两条曲线分别为Q 、 P 两地某日太阳高度日变化情况。

则 A ．Q 地昼长小于12小时 B ．P 地该日正午旗杆影长为零 C ．Q 地一定位于北半球 D ．P 地一年中有两次太阳直射4．若a 、b 两曲线分别为X 、Y 两地某日太阳高度 日变化情况。

则A ．X 、Y 两地纬度值相同B ．X 、Y 两地昼长相同C ．X 、Y 两地处在同一经线上D ．X 、Y 两地太阳高度相同 5．若a 、b 两曲线分别为Z 地一年内两天的太阳高度日变化情况。

则A ．Z 地有极昼极夜现象B ．Z 地位于五带中的北温带C ．Z 地可能位于拉丁美洲D ．Z 地可能位于印度下图为杭州（30°N ）某地某座山峰的等高线示意图（单位：米），甲乙为两处风景点,沿虚线L 1坡度为30°，沿虚线L 2坡度为45°。

读图回答6～8题6A.6月下旬B.10月初C.11月中旬D.12月中旬7．不考虑天气因素，元旦日乙地A.上午无日照B.正午无日照C.白天都无日照D.白天都有日照8.在两个风景点中,夏天游客多选择乙地看日出,对此解释不．合理的是A.乙地位于甲地的西北，日出更早B.乙地海拔更高的，视野更开阔C.甲地海拔低，凌晨冷空气易集聚，大雾天气多D.夏天日出在东北方，乙地观日出视线更佳下图为地球某时刻太阳高度分布示意图，图中粗线为等太阳高度线。

学必求其心得，业必贵于专精金华一中2011—2012 学年高三第二次月考英语试卷(2011年10月）本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共150分。

考试时间120分钟。

第I卷(选择题，共100分)第一部分:英语知识运用(共两节, 满分50分）第一节：单项填空（共20小题，每小题1分,满分20分）从A、B、C、D四个选项中,选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

1. -I’m terribly sorry I forgot your name just now!—________—it happens to all of us！A。

You bet B. Think nothing of it C。

Bingo D。

Certainly not2. ________ price he paid，he wasted his money。

A。

However low a B. However low C。

Whatever low D。

No matter low3. Cancer is one of the top killer diseases nowadays and scientists have found out that stresshelps to bring it ________.A. up B。

down C。

out D。

on4。

The horse，though ________ native to Europe, was brought to the North American continent by Spaniards.A。

/ B. was C. be D. were5。

Tom started learning the ________ of engineering with the help of an engineer.A. TNT B。

VIP C。

单元过关检测(教师附赠)(时间：90分钟满分：100分)一、选择题(每小题2分，共50分)1．20世纪50年代我国提出的外交方针、原则，至今仍富有生命力并被广泛运用的是( )①“求同存异”方针②反对霸权主义强权政治③和平共处五项原则④发展与第三世界国家的友好合作关系A．①②③ B．②③C．①③ D．③④解析：本题应注意20世纪50年代提出，现在还有生命力并被运用。

答案：C3． (珠海市2012届高三9月摸底，18)1955年4月，毛泽东主席曾撰文提出：“应把五项原则扩展到所有国家的关系中去。

”他还说：“中国愿意同一切国家包括美国在内和平共处。

”下列相关认识中，正确的是( )A．此后，美国很快就派基辛格秘密访华B．和平共处五项原则最初是为了处理好中国与邻国关系而定的C．毛泽东主席的话标志着中国要放弃“一边倒”的外交政策D．毛泽东主席见证了中美建交的过程解析：把握时间信息1955年，A项为1971年，C项为1958年中苏关系恶化后，D项为1979年，毛主席已经逝世，和平共处五项原则最初是中国处理与印度和缅甸关系时提出的，选择B项。

答案：B4． (金华一中2012届高三第二次月考，19)周恩来在一次国际会议上说：“中华人民共和国对于目前正在她的邻邦进行的战争和战争扩大的危险，不能不加以密切的关注。

中国人民认为：朝鲜战争停止了，现在，印度支那战争同样应该停止。

”这次会议应是( )A．亚非会议B．日内瓦会议C．旧金山会议D．第26届联大5． (2011年高考江苏卷，10)日内瓦会议后，毛泽东就外交问题指出：“关门关不住，不能关，而且必须走出去。

”这里，“必须走出去”的战略意义在于( )A．缓和中苏关系恶化的局面B．行使安理会常任理事国的权力C．重建中美间战略伙伴关系D．发挥在国际关系中应有的作用解析：本题考查历史知识的理解和材料解读能力。

日内瓦会议时间是1954年，周恩来总理率团出席，是新中国成立后第一次以大国身份参加的国际会议。

浙江省部分地市2000年与2010年常住人口变化图1002003004005006007008009001000杭州温州宁波嘉兴衢州丽水舟山-0.50%0.00%2.00%2.50%金华一中高三年级12月月考地理 测试日期：2012年12月28日一． 单项选择题（26小题每错一题扣2分，共计48分）。

我国以2010年11月1日零时为标准时点进行了第六次全国人口普查。

下面是我省部分地市近两次人口普查反映的常住人口变化图。

读图完成1-2题。

1．据图判断，下列叙述正确的是A ．人口增幅：温州﹥宁波B ．人口增长模式：宁波过渡型，舟山现代型C ．年均自然增长率：衢州﹤丽水D ．年均增长率：嘉兴﹤杭州2．据图分析，正确的是A ．2010年杭州的常住人口最多，主要是受历史和政治因素影响B ．温州市的人口增长率高于全省平均水平，是因为发达的经济吸引大量外来人口C ．丽水市的负增长是因该市人口老龄化严重D ．舟山市的常住人口最少，主要是因为淡水资源缺乏由世界银行委托撰写的一份最新研究报告显示，如果世界不能采取有效行动应对气候变化，到本世纪末，全球气温将上升4摄氏度，并引发一系列灾难性的变化。

据此完成3-4题。

3．珠峰的冰川大量消融最可能导致的环境问题是A ．致使河流中上游水土流失加剧B ．致使河流中下游洪涝灾害频繁C ．南亚各国的粮食产量不断提高D ．影响水资源的可持续利用 4．导致全球变暖的人为原因主要有①世界人口的不断增长 ②石油、煤炭等燃烧时大量释放温室气体 ③对森林资源的过度索取④人类在使用冰箱、空调等电器时排放出氟氯烃 ⑤交通运输业的快速发展A．①④⑤B．①③⑤C．②③④D．②③⑤资源诅咒系数是一个衡量地区经济发展（主要是第二产业发展）与地区资源优势偏离程度的指标，指数值越大，表示资源没有带来相应的财富增长和区域经济发展。

读图完成5-6题。

5. 山西省资源诅咒系数居高不下，可能的原因有①产业结构单一；②经济发展缓慢；③生态环境脆弱；④人均资源占有量高；⑤吸引外资能力弱A．①②④B．②③⑤C．③④⑤D．①③⑤6. 推测下列省区资源诅咒系数最低的是A．贵州B．上海C．内蒙古D．青海国家就业结构(一:二:三产业)失业率(%)贫穷人口比例(%)前10%收入家庭占总消费的比例(%)后10%收入家庭占总消费的比例(%)外债(亿美金)出口值(亿美金)进口值(亿美金)甲5：23：72 7.9 30.0 32.6 1.2 128.6 68.0 52.6 乙7：24：69 3.3 15.0 24.2 2.7 370.1 466.3 417.9 丙42：20：38 1.2 9.6 33.7 1.6 82.5 191.3 156.9 丁85：6：9 14.0 64.0 38.8 1.2 3.5 6.5 4.9 7．四个国家中，贫富差距最小的国家是A．甲B．乙C．丙D．丁8. 丁国的人口增长最可能处在哪个阶段A．高-高-低模式B．由高-低-高向三低模式转变C．高-低-高模式D．低-低-低模式下图是以极点为中心的半球图，箭头表示洋流的分布位置及流向。