洛伦兹速度变换公式

洛伦兹变换速度公式
洛伦兹变换速度公式是v'x = (vx-vt)/(1-v^2/c^2)^(1/2)，v'y = vy，v'z = (vz-vt)/(1-v^2/c^2)^(1/2)。

其中，v是观察者的速度，c是光速，t是时间，x、y、z是观察者在静止坐标系中的坐标，x'、y'、z'是观察者在移动坐标系中的坐标。

这个公式可以用来计算在相对运动中两个坐标系之间的坐标变换。

例如，如果你在高速火车上向北方移动，那么从地面上的观察者看来，你的位置将会发生偏移。

同样地，如果你在高速移动的飞机上向地面上的某一点投掷一个物体，那么从地面上的观察者看来，物体的轨迹将会发生弯曲。

这些都是洛伦兹变换所描述的现象。

洛伦兹变换公式不仅在狭义相对论中有着重要的应用，在广义相对论中也有着重要的应用。

在广义相对论中，时空被认为是一种弯曲的几何结构，而洛伦兹变换则可以用来描述在不同的弯曲时空之间的坐标变换。

此外，洛伦兹变换也是现代物理学中许多重要概念的基础，如量子力学的波函数、粒子自旋、量子纠缠等，都与洛伦兹变换有关。

因此，洛伦兹变换是现代物理学中非常重要的一个概念。

洛伦兹速度变换式
洛伦兹速度变换式是指在相对论中，两个参考系之间的速度变换关系。

它由荷兰物理学家洛伦兹于1904年提出，是狭义相对论的基本公式之一。

该公式描述了当两个参考系相对运动时，其中一个参考系中的物
体的速度在另一个参考系中的表现形式。

洛伦兹速度变换式的表达式为：
v' = (v - u) / (1 - v*u/c^2)
其中，v'表示在另一个参考系中观察到的物体速度；v表示在原来的参考系中观察到的物体速度；u表示两个参考系之间相对运动的速度；c
表示真空中光速。

这个公式可以解释为：当两个参考系相对运动时，一个在第一个参考
系中以速度v运动的物体，在第二个参考系中以速度v'运动。

这个公
式告诉我们，在相对论中，物体的速度不是简单地加起来，而是通过
这个公式进行计算。

需要注意的是，在经典力学中，两个参考系之间进行速度变换时使用
的是加法规则。

但在相对论中，使用加法规则会导致矛盾和错误。

因
此需要使用洛伦兹变换公式进行速度变换。

除了速度变换外，洛伦兹变换还包括时间变换和长度变换。

这些变换都是相对论中的基本公式，它们描述了物理量在不同参考系之间的表现形式。

总之，洛伦兹速度变换式是狭义相对论中的重要公式之一。

它描述了两个参考系之间的速度变换关系，并告诉我们在相对论中物体速度的计算方法。

理解和应用这个公式对于研究相对论和解决相关问题具有重要意义。

洛倫玆因子表達式
洛倫茲因子表达式，也称为洛伦兹因子公式，是描述相对论中速度与时间之间关系的数学表达式。

该表达式是洛伦兹变换的一部分，用于计算物体在不同参考系中的时间、长度和质量的变化。

洛伦茲因子表达式可以写成：
γ = 1 / √(1 - v² / c²)
其中，γ表示洛伦茨因子，v表示物体的相对速度，c表示光速。

这个公式表明了在相对论中，物体的时间、长度和质量都受到速度的影响。

当物体静止时，即v=0时，洛伦茨因子为1，相
对论效应可以忽略不计。

随着速度的增加，洛伦茨因子逐渐增大，时间变慢，长度缩短，质量增加。

洛伦茲因子的导出基于爱因斯坦的狭义相对论理论，它对传统的牛顿运动学提出了一种修正，解释了接近光速的速度下，时间和空间的相对性。

在粒子物理学、天体物理学等领域，洛伦茨因子在描述高速物体运动和相对论效应时起着关键作用。

第十四章相对论基础
§14.4 新的变换关系—洛伦兹变换
《大学物理》校级精品课程教学团队
x
•一、洛伦兹坐标变换式
•爱因斯坦认识到时间和长度的概念没有绝对意义，他相对性原理和光速不变原理出发
v
-可得
ï
ïì--=21'vt x x u
ï
ï
ïì
-=1'u u x
洛伦兹速度变换公式如果
或
('u
)
u和
三、洛伦兹速度变换的意义
• 1 解决了电磁学与相对性原理的矛盾：爱因斯坦证明了在各个惯性系中，麦克斯韦方程组的形式相同。

• 2 解决了光速不变与相对性原理的矛盾：
• 3 相对性原理及其时空观是狭义相对论的思想实质，洛伦兹变换是其表现形式，通过光速不变原理将二者联系起来。

尽管在爱因斯坦之前一年，洛伦兹和庞加莱已经推出了洛伦兹变换，和长度收缩等假说，但是他们是从以太存在的电子论的角度得出的，所以没有得出狭义相对论。

四、洛伦兹变换和伽利略变换间的关系
•从洛伦兹变换可以看到，当两个惯性系之
间的相对速度
例两个婴儿A
同时出生。

若一宇宙飞船沿两医院的连线方向由飞行时，测得
员认为A、B
教材P161: 14-11。

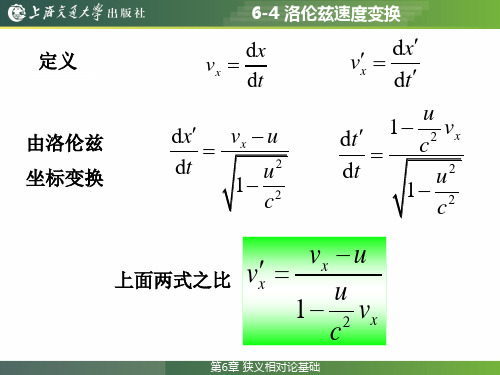
写出洛伦兹变换数学表达式
洛伦兹变换公式是a=dv/dt,v=v0+∫adt。

由麦克斯韦方程组可以得到电磁波的波动方程，由波动方程解出真空中的光速是一个常数。

按照经典力学的时空观，这个结论应当只在某个特定的惯性参照系中成立，这个参照系就是以太。

其它参照系中测量到的光速是以太中光速与观察者所在参照系相对以太参照系的速度的矢量叠加。

然而1887年的迈克耳孙-莫雷实验测量不到地球相对于以太参照系的运动速度。

1904年，洛伦兹提出了洛伦兹变换用于解释迈克耳孙-莫雷实验的结果。

根据他的设想，观察者相对于以太以一定速度运动时，长度在运动方向上发生收缩，抵消了不同方向上由于光速差异，这样就解释了迈克耳孙-莫雷实验的零结果。

动量能量洛伦兹变换动量能量洛伦兹变换是相对论中非常重要的概念，它描述了物体在不同参考系下动量和能量的变化。

以下将介绍动量能量洛伦兹变换的定义、公式、特点以及应用。

一、定义动量能量洛伦兹变换是指当一个物体在不同参考系下运动时，其动量和能量会发生变化。

这种变化是由于相对论效应引起的，即速度越快，质量越大。

二、公式根据洛伦兹变换的基本原理，可以得到动量和能量的洛伦兹变换公式：1. 动量的洛伦兹变换公式：p' = γ(p - βE/c)其中p为原来物体的动量，p'为新参考系下物体的动量，γ为洛伦兹因子（γ=1/√(1-β²)，β为物体速度除以光速c），E为物体总能量。

2. 能量的洛伦兹变换公式：E' = γ(E - βpc)其中E为原来物体的总能量，E'为新参考系下物体的总能量，p为原来物体的动量。

三、特点1. 非线性：与经典力学中线性关系不同，在相对论中，动量和能量的变化是非线性的。

2. 速度越快，质量越大：当物体的速度接近光速时，γ会趋向无穷大，物体质量也会趋向无穷大。

3. 质能等价：根据爱因斯坦的质能关系E=mc²，物体的能量也可以看作是其质量的一种表现。

因此，在相对论中，动量和能量可以互相转化。

四、应用动量能量洛伦兹变换在实际应用中有着广泛的应用。

以下是一些例子：1. 粒子加速器：粒子加速器利用电磁场加速带电粒子到极高的速度，这时就需要考虑相对论效应对粒子运动轨迹、动量和能量的影响。

2. 核反应堆：核反应堆产生的高速中子在与原子核碰撞时会发生散射或吸收反应。

由于中子与原子核碰撞前后具有不同的动量和能量，在计算反应截面等参数时需要考虑相对论效应。

3. 天文学：天文学中研究宇宙射线、恒星运动等问题都需要考虑相对论效应对动量和能量的影响。

总之，动量能量洛伦兹变换是相对论中非常重要的概念，它不仅影响着物体的运动轨迹、动量和能量，也广泛应用于现代科学技术领域。

洛伦兹变换的速度公式洛伦兹变换是描述相对论情况下空间时间坐标之间的关系的数学方法。

在狭义相对论中，当观察者的参考系以速度v相对于光速运动时，由于光速不变原理，时间和空间会发生相对论效应的变换。

速度变换公式推导假设存在两个参考系，分别为S系和S’系，S’系以速度v相对于S系运动。

考虑一个运动速度为u相对于S系的物体，我们要求其在S’系中的速度u’。

根据洛伦兹变换，时间的变换公式为：$$ \\Delta t' = \\gamma (\\Delta t - \\frac{v}{c^2} \\Delta x) $$空间的变换公式为：$$ \\Delta x' = \\gamma (\\Delta x - v \\Delta t) $$其中，$\\gamma = \\frac{1}{\\sqrt{1 - \\frac{v^2}{c^2}}}$。

考虑速度是空间坐标对时间的导数，即$u = \\frac{dx}{dt}$，$u' =\\frac{dx'}{dt'}$，代入变换公式，得到速度变换的公式为：$$ u' = \\frac{dx'}{dt'} = \\frac{\\gamma(dx - vdt)}{\\gamma(dt -\\frac{v}{c^2}dx)} $$将dx=udt代入，整理得到：$$ u' = \\frac{U - v}{1 - \\frac{vU}{c^2}} $$其中，U为速度u的分量，即U = u/c。

结论洛伦兹变换的速度变换公式表达了相对论情况下，观察者在不同参考系中测得的物体速度之间的关系。

这个公式揭示了在相对论情况下速度的变换会受到光速不变原理的影响，导致速度的合成与经典物理中不同。

通过相对论性的速度变换公式，我们可以更好地理解相对论情况下的运动问题。

洛伦兹变换的推导洛伦兹变换是描述物理学中相对论性质的基本工具之一。

它描述了时间、空间和运动之间的关系，并告诉我们在不同惯性参考系中看到的真实时间和空间是如何变化的。

下面我们将会介绍洛伦兹变换的推导过程。

推导过程：假设我们有一个以速度为v运动在x轴上的物体，用伽利略变换我们可以知道它在不同惯性参考系上的位置变化。

但是在相对论中，物体运动状态的描述需要使用洛伦兹变换。

为了简化问题，我们将考虑一个事件的发生，即在一个参考系中一个粒子在时间t0,位置x0处发生了一个事件。

现在我们要求在另一个相对这个参考系以速度v运动的参考系S'中，这个事件的时间和位置分别是多少。

首先，我们需要定义两个参考系之间的相对速度和时间的概念。

两个参考系S和S'之间相对速度的定义为在S参考系中测量的S'参考系的速度v。

时间差也需要考虑，即两个参考系的时间零点并不一定相同。

我们假设两个参考系之间有一把尺子，这样我们可以用一个数来表示两个事件的时间和空间间隔。

在S参考系中，事件的时间和位置可以分别表示为t0和x0。

在S'参考系中，我们要求时间t'和空间位置x'。

我们现在将要根据下列的公式来推导洛伦兹变换：x' = γ(x-vt)t' = γ(t-xv/c²)其中γ是一个常数，它被称为洛伦兹因子，定义为γ=1/√(1-v²/c²)，其中c表示光速。

现在我们需要利用尺子和两个参考系之间的速度来计算x'和t'。

首先，我们需要确定在S'系统中事件的位置。

假设我们在S系统中看到一个长度为L0的物体在移动，那么在S'系统中这个物体的长度将会是L'=L0/γ。

这个长度补偿称为“同时错误”，因为S'系统与S系统看到的时间可能不同，所以用S系统的时间去测量S'系统的物体长度时，会出现长度感缩小的情况，需要使用修正后的长度L'。