当前位置：文档之家 › 双目视觉三维重构公式

双目视觉三维重构公式

  • 格式：doc
  • 大小：233.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

转OpenCV学习笔记17双目测距与三维重建

转OpenCV学习笔记17双目测距与三维重建

转OpenCV学习笔记17 双目测距与三维重建三、双目定标和双目校正双目摄像头定标不仅要得出每个摄像头的内部参数，还需要通过标定来测量两个摄像头之间的相对位置(即右摄像头相对于左摄像头的三维平移t和旋转R参数)。

图6要计算目标点在左右两个视图上形成的视差，首先要把该点在左右视图上两个对应的像点匹配起来。

然而，在二维空间上匹配对应点是非常耗时的，为了减少匹配搜索范围，我们可以利用极线约束使得对应点的匹配由二维搜索降为一维搜索。

图7而双目校正的作用就是要把消除畸变后的两幅图像严格地行对应，使得两幅图像的对极线恰好在同一水平线上，这样一幅图像上任意一点与其在另一幅图像上的对应点就必然具有相同的行号，只需在该行进行一维搜索即可匹配到对应点。

图8 1.关于cvStereoCalibrate的使用如果按照Learning OpenCV的例程，直接通过cvStereoCalibrate来实现双目定标，很容易产生比较大的图像畸变，边角处的变形较厉害。

最好先通过cvCalibrateCamera2()对每个摄像头单独进行定标，再利用cvStereoCalibrate进行双目定标。

这样定标所得参数才比较准确，随后的校正也不会有明显的畸变。

我使用的程序主要基于Learning OpenCV的例程ch12_ex12_3.cpp，其中主要部分如下：///////////////////////////////////////////////////////////////// ///////////是否首先进行单目定标?cvCalibrateCamera2(&_objectPoints,&_imagePoints1,&_npoints,imageSi ze,&t_M1,&t_D1,NULL,NULL,CV_CALIB_FIX_K3)；cvCalibrateCamera2(&_objectPoints,&_imagePoints2,&_npoints,imageSize, &t_M2,&t_D2,NULL,NULL,CV_CALIB_FIX_K3)；///////////////////////////////////////////////////////////////////// ///////进行双目定标cvStereoCalibrate(&_objectPoints,&_imagePoints1,&_imagePoints2,&_npoi nts,&t_M1,&t_D1,&t_M2,&t_D2,imageSize,&t_R,&t_T,&t_E,&t_F,cvTermCrite ria(CV_TERMCRIT_ITER+CV_TERMCRIT_EPS,100,1e-5))；//flags为默认的CV_CALIB_FIX_INTRINSIC上面的t_M1(2),t_D1(2)分别是单目定标后获得的左(右)摄像头的内参矩阵(3*3)和畸变参数向量(1*5)；t_R,t_T分别是右摄像头相对于左摄像头的旋转矩阵(3*3)和平移向量(3*1),t_E是包含了两个摄像头相对位置关系的Essential Matrix(3*3)，t_F则是既包含两个摄像头相对位置关系、也包含摄像头各自内参信息的Fundamental Matrix(3*3)。

关于双目立体视觉的三大基本算法及发展现状的总结

关于双目立体视觉的三大基本算法及发展现状的总结

关于双目立体视觉的三大基本算法及发展现状的总结来源｜3D视觉工坊双目立体视觉一直是机器视觉研究领域的发展热点和难点，“热”是因为双目立体视觉有着及其广阔的应用前景，且随着光学、计算机科学等学科的不断发展，双目立体技术将不断进步直到应用到人类生活的方方面面。

“难”则是因为受到摄像机、镜头等硬件设备及一些相关算法的限制，双目立体视觉的研究及如何更好的应用到生产实际中仍有待在座的各位去进行突破。

一.简介双目立体视觉是机器视觉中的一个重要分支，自上世纪60年代中期开创以来，经过几十年的发展，如今在机器人视觉、航空测绘、军事应及医学成像、工业检测上应用极其广泛。

双目立体视觉基于视差原理并利用成像设备从不同的位置获取被测物体的左右两幅图像，然后根据三角测量原理计算空间点在二维图像的位置偏差，最后再利用位置偏差进行三维重建来获取被测物体的三维几何信息（本文不对双目立体视觉的数学原理进行详细介绍）。

二.双目立体视觉的三大基本算法的原理及其代码实现（基于opencv）双目立体视觉中常用的基于区域的局部匹配准则主要有图像序列中对应像素差的绝对值之和SAD（sum of absolute differences）、对应像素差的平方之和SSD（sum of squared differences）及半全局匹配算法SGM（semi—global matching）。

2.1 SAD（sum of absolute differences）的原理匹配算法SAD的基本思想是对经行对准后的左右视图图像的对应像素块的对应像素差的绝对值进行求和。

其数学公式如下：SAD匹配算法的基本流程如下：①输入两幅已经校正实现行对准的左视图（Left-Image）及右视图（Right-Image）。

②对左视图Left-Image进行扫描选定一个锚点并构建一个类似于卷积核的小窗口。

③用此小窗口覆盖Left-Image，并选择出小窗口覆盖区域的全部像素点④同样用此小窗口覆盖Right-Image，并选择出小窗口覆盖区域的全部像素点。

《双目立体视觉三维重建的立体匹配算法研究》

《双目立体视觉三维重建的立体匹配算法研究》

《双目立体视觉三维重建的立体匹配算法研究》一、引言双目立体视觉技术是计算机视觉领域中的一项重要技术，其通过模拟人类双眼的视觉系统，利用两个相机从不同角度获取场景的图像信息，进而实现三维重建。

而立体匹配算法作为双目立体视觉三维重建中的关键技术，其准确性和效率直接影响到三维重建的效果。

本文旨在研究双目立体视觉三维重建中的立体匹配算法，分析其原理、优缺点及改进方法，为进一步优化三维重建效果提供理论支持。

二、双目立体视觉原理双目立体视觉原理基于视差原理，即通过两个相机从不同角度拍摄同一场景，获取场景的左右两个视图。

通过分析这两个视图中的像素对应关系，可以计算出场景中各点的三维坐标，从而实现三维重建。

其中，立体匹配算法是获取像素对应关系的关键。

三、立体匹配算法研究3.1 算法概述立体匹配算法是双目立体视觉三维重建中的核心算法，其主要任务是在左右视图中寻找对应点。

常见的立体匹配算法包括基于区域、基于特征和基于相位的方法。

这些方法各有优缺点，适用于不同的场景和需求。

3.2 基于区域的立体匹配算法基于区域的立体匹配算法通过计算左右视图中的像素灰度或颜色差异来寻找对应点。

该方法具有较高的匹配精度，但计算量大，易受光照、噪声等因素的影响。

常见的基于区域的立体匹配算法包括块匹配法、区域生长法等。

3.3 基于特征的立体匹配算法基于特征的立体匹配算法通过提取左右视图中的特征点（如角点、边缘等），然后根据特征点的相似性进行匹配。

该方法具有较高的鲁棒性，对光照、噪声等有一定的抵抗能力。

常见的特征提取方法包括SIFT、SURF等。

3.4 算法优缺点及改进方法每种立体匹配算法都有其优缺点。

例如，基于区域的算法精度高但计算量大；基于特征的算法鲁棒性高但可能丢失部分细节信息。

针对这些问题，研究者们提出了多种改进方法，如结合多种算法的优点进行融合匹配、优化特征提取和匹配策略等。

此外，随着深度学习和人工智能的发展，基于深度学习的立体匹配算法也逐渐成为研究热点，其在复杂场景下的匹配效果有了显著提升。

双目立体视觉系统教材

双目立体视觉系统教材


双目立体视觉三维 测量是基于视差原 理。 计算公式：
10
3D坐标计算
双目立体视觉系统
11
光轴平行模型3D坐标计算
则三维坐标为(X/W, Y/W, Z/W).
双目立体视觉系统 12
双目视觉系统模型
光轴会聚模型
O，O’分别为相机光心，
光轴会聚模型3D坐标计算（1）
O，O’分别为相机光心，
X u1 Y M Zc1 v left 1 Z 1 1
42
图像匹配方法
图像匹配方法
图像匹配方法
图像匹配方法
图像匹配方法
特征匹配 VS 区域匹配

特征匹配 (Feature match)：



速度快，匹配效率高； 特征的提取可以到亚像素级别，精度较高； 匹配元素为物体的几何特征，对照明变化不敏感； 重建需要拟合。 重建不需要拟合； 速度慢，效率低； 对于无纹理，纹理不明显的图像匹配效果不理想； 对光强、对比度、照明条件敏感。
极线几何 (Epipolar Geometry)




基线：左右两像 机光心的连线； 极平面：空间点 ，两像机光心决 定的平面； 极点：基线与两 摄像机图像平面 的交点； 极线：极平面与 图像平面的交线 。
P Pl 极平面 Pr
极线
p l p r
Ol
el 极点
er 基线
Or
33
极线几何 (Epipolar Geometry)
两个摄像机之间的几何关系可以用以下R 和 t 表示：
主要内容
1：双目视觉系统模型
2：双目视觉系统关键技术 •系统标定 •立体匹配 •3D重建及后续处理

基于双目立体视觉的三维重构研究

基于双目立体视觉的三维重构研究

基于双目立体视觉的三维重构研究一、本文概述随着科技的不断发展，三维重构技术在许多领域，如机器人导航、自动驾驶、虚拟现实、增强现实、医疗诊断以及工业检测等，都发挥着越来越重要的作用。

在众多三维重构技术中，基于双目立体视觉的三维重构方法因其设备简单、成本低廉、实时性强等特点而备受关注。

本文旨在探讨基于双目立体视觉的三维重构技术的研究现状、基本原理、关键技术和应用前景，以期对这一领域的研究者和实践者提供有益的参考和启示。

本文将首先介绍双目立体视觉三维重构的基本原理，包括双目视觉的成像模型、立体匹配算法以及三维坐标计算等。

接着，将详细分析当前双目立体视觉三维重构技术中的关键问题，如视差计算、图像预处理、遮挡和纹理映射等，并探讨相应的解决方法和技术。

本文还将对双目立体视觉三维重构技术在不同领域的应用案例进行介绍，分析其优势和局限性，并展望未来的发展趋势和应用前景。

通过本文的研究，我们希望能够为基于双目立体视觉的三维重构技术的发展提供新的思路和方法，推动这一领域的技术进步和应用发展。

我们也希望本文能够为相关领域的学者和工程师提供有益的参考和借鉴，共同推动三维重构技术的发展和应用。

二、双目立体视觉原理双目立体视觉是人类和许多动物天生具备的一种空间感知能力，通过两只眼睛从稍微不同的角度观察物体，然后大脑综合这两个不同的视觉信号，形成立体视觉。

这种视觉原理为三维重构提供了重要的理论基础。

在双目立体视觉系统中，两个相机（模拟双眼）从不同的位置观察同一物体，得到两幅具有视差的图像。

视差是指同一物体在左右两幅图像中的像素坐标之差。

视差的大小取决于相机的基线距离（两个相机光心之间的距离）和物体到相机的距离。

物体距离相机越近，视差越大；物体距离相机越远，视差越小。

为了从这两幅图像中恢复物体的三维形状，我们需要利用三角测量的方法。

在三角测量中，我们知道相机的内外参数（包括相机的内参矩阵、畸变系数、旋转矩阵和平移向量等），通过匹配两幅图像中的同名点（即同一物体在两个图像中的像素坐标），可以计算出这些点在世界坐标系中的三维坐标。

双目立体视觉下的计算机的三维重建方法

双目立体视觉下的计算机的三维重建方法
处 理措施 和 管理机 制 。不仅仅 是 一种 全新 的视 觉理论 框 架 ，也是 应 用在 立体 匹配技 术 中的 关键 要 素。本 文对 双 目立体视 觉下计 算机 三维 重建 算 法进行 简要 分析 ，并 对仿 真结 果 以及 实验 结果展 开 了讨论 ， 旨在 为相 关研 究人 员提 供 有价值 的参 考建 议 。
Ｅ Ｌ Ｅ Ｃ Ｔ Ｒ ＯＮ Ｉ Ｃ Ｓ ＷＯ Ｒ Ｌ Ｄ・计 算 机 的 三 维重 建 方 法
天 津港航 工程 有 限公 司 王 昶
【 摘要 】 双 目立体 匹配项 目 是双 目立体视 觉中重要的组成部分，也是关键性的应用步骤，需要相关研究人员结合实际需求建构更加 系统化的
【 关键词 】 双 目立体视觉；计算机 ；三维重建；结果分析
三维 重建 项 目中 ，获取 三维信 息 的路径 主要 分为 ３ Ｄ Ｍａ ｘ 和Ａ ｕ ｔ ｏ Ｃ Ａ Ｄ等建模软件对相关信息参数进行组织和处理，并且利用视频 以及图 像管理措施对其进行数据分析，从而重建最接近真实场景的三维模 型。 集 数据 等信 息进 行集 中处理 ，并且 将 其和 真实 场景 的立 体 图像进 行 有效 的匹配 ，像 素大 小为 ５ ｌ ２ ｂ ｉ ｔ ｓ ＊ ＊ ５ １ ２ ｂ ｉ ｔ ｓ ＊ 。 首 先 ，在视 差搜 索 范 围过小 的情 况下 ，灰 度 的范 围也 会减 少 ， 人像 中会 出现 很多 的误 判 匹配 点，而 随着 范 围的增 大 ，会 导致视 差 图 的对 比度逐 渐增 强 ，若是 搜索 范 围增大 ，则 视差 图的腐蚀 问题也 会 随之 增 大 。正是 基于 此 ，在对 相关 数据 进行 分析 和辨 别之 后 ，能 对 匹配 搜 索范 围进 行初 步 确定 ，在 ０ — １ ９ 之 间是 最佳 视 差搜 索范 畴 ， 且匹配 视 差 图的效果 也较 好【 ３ 】 。 其 次 ，相 较于传 统 匹配 结构 ，预 先估 计 的视差 搜 索范 围能 有效 去 除错误 匹配 点和 多重 匹配 点 ，一定 程度 上减 少 匹配 耗时 。正 是基 于此 ，在 对误 差 阈值进 行处 理 时，相 关机 制 能有效 滤 除一 部分 不可 信 的视差 估计 点 ，也能 保证 边缘 纹理 更加 的清 晰 ，真 正意 义上 降低 了匹配 的误判和 噪 声，升 级准 确性 】 。 ２ ． ２ 双 目立体 视觉 下计 算机 三维 重建 实验 结果分 析 构建 简单 和横 向平 行配 置 的双 目立 体视 觉系 统 ，将相 关参 数进 行有 效处 理 ，根据 相关 参数 建立 数 学模 型 ，利 用视 差 测距 法对 真实 场景 的深 度和 信 息进行 处理 ，并对其 进行 计算 后 ，建 构三 维信 息 的 同时，利 用立 体 匹配算 法 负三 维信 息进 行有 效恢 复 ，能真 正 实现三 维真 实场 景 的还原和 重建 ，也 能有 效完 成相 关参 数指 标 。 传 统 的特 征 匹 配 算 法 以及 区域 匹 配 算法 都 有 自身 的 优 势 和 特 征 ，在 此 基 础 上 改进 相 关 算 法 模 型 ，确 保 视 差 图 的 可靠 性 符 合 标 准 ，并且 利用 角 点匹配 预估 措施 对视 差搜 索 空 间进 行 有效 处理 ，从 而 减少 匹配 耗时 。基础 算 法在 满足 实时 性要 求 的基础 上 ，能 在提 升 视 差 图精 度 的 同时 ，保 证 三维 重建 结构 的完 整性 ，也 能更 好地 落 实 相 对应 的深 度 图 ，从而 顺利 完 成 真实场 景 的 三维 重 建 】 。结合 特 征 匹 配算 法 以及 区域 匹配算 法 ，能对 不 同的优 缺 点进 行改 进 ，从而 提 高基 本特 征 的处 理效 果 ，落实 分布 立体 模 型的有 效性 ，利 用 相关 算 法 对最 佳时 差 的搜索 范 围进行 处理 ，从 而有 效 的建 立相 应 的区域 匹 配 结构 ， 只有保 证误 差 能量视 域数 值和 滤 除 图像 数 值之 间 的不可 行 视 差预估 点符 合标 准 ，才 能提高 图像 的处 理效 果【 ６ 】 。

《双目立体视觉三维重建的立体匹配算法研究》

《双目立体视觉三维重建的立体匹配算法研究》一、引言双目立体视觉技术是计算机视觉领域中重要的三维重建技术之一。

它通过模拟人类双眼的视觉系统，利用两个相机从不同角度获取同一场景的图像，然后通过立体匹配算法对两幅图像进行匹配，从而获取场景的三维信息。

本文旨在研究双目立体视觉三维重建中的立体匹配算法，探讨其原理、方法及优化策略。

二、双目立体视觉基本原理双目立体视觉的基本原理是基于视差原理，即人类双眼从不同角度观察同一物体时，会在大脑中形成立体的视觉效果。

在双目立体视觉系统中，两个相机从不同位置和角度拍摄同一场景，得到两幅具有一定视差的图像。

通过分析这两幅图像中的对应点，可以计算出场景中物体的三维信息。

三、立体匹配算法研究立体匹配算法是双目立体视觉三维重建的核心。

其基本思想是在两个视图中寻找对应点，然后根据对应点的位置差异计算视差图。

目前，常见的立体匹配算法包括基于区域、基于特征、基于相位和基于全局优化等方法。

3.1 基于区域的立体匹配算法基于区域的立体匹配算法通过比较两个视图中的像素或区域来寻找对应点。

其优点是简单易行，但容易受到光照、遮挡、噪声等因素的影响。

为了提高匹配精度和鲁棒性，研究者们提出了多种改进方法，如引入多尺度、多方向信息、使用自适应阈值等。

3.2 基于特征的立体匹配算法基于特征的立体匹配算法首先提取两个视图中的特征点，然后根据特征点的匹配关系计算视差图。

该类算法具有较高的鲁棒性和精度，尤其在处理复杂场景和动态场景时表现出较好的性能。

为了提高特征提取和匹配的效率，研究者们不断探索新的特征描述符和匹配策略。

3.3 优化策略为了提高立体匹配算法的性能，研究者们提出了多种优化策略。

其中包括引入半全局匹配算法、使用多视差图融合技术、引入深度学习等方法。

这些优化策略可以有效提高匹配精度、降低误匹配率，并提高算法的鲁棒性。

四、实验与分析为了验证本文所研究的立体匹配算法的性能，我们进行了大量实验。

实验结果表明，基于特征的立体匹配算法在处理复杂场景和动态场景时具有较高的精度和鲁棒性。

基于双目视觉的猪体体尺参数提取算法优化及三维重构共3篇

基于双目视觉的猪体体尺参数提取算法优化及三维重构共3篇基于双目视觉的猪体体尺参数提取算法优化及三维重构1近年来，基于双目视觉的猪体尺参数提取算法在猪育种中应用越来越广泛。

通过利用猪体图像的立体信息，可以准确地提取出猪的身高、体长、胸围等参数，以辅助猪育种工作，进而提高猪的育种效率。

但是，由于生物体的形态复杂且多变，以及猪体表面的毛发、皮肤等干扰因素的存在，猪体尺参数的提取一直存在误差率较高的问题。

因此，如何优化猪体尺参数提取算法，并实现三维重构，已经成为研究的热点。

本文旨在提出一种基于双目视觉的猪体尺参数提取算法，并进行优化，最终实现猪的三维重构。

该算法的基本思路是，通过采集猪的左右两个视图图像，进行图像预处理，包括去除背景、提取猪体等操作，再利用立体匹配算法，计算出左右两张图像之间的视差信息。

根据视差信息，可以得到猪体上各个点的三维坐标，进而实现对猪体尺参数的提取。

具体流程如下：1. 采集猪的左右两个视图的图像，并进行图像去除背景处理。

这一步的目的是将猪体的轮廓从背景中分离出来，以便后续的猪体提取操作。

2. 猪体提取。

本文采用基于深度学习的猪体识别算法，对猪体进行提取。

该算法的基本思路是，通过训练深度神经网络，学习对猪体的特征进行提取，从而实现对猪体的自动分割。

3. 立体匹配。

通过计算左右两张图像之间的视差信息，得到猪体各点的三维坐标。

该算法采用经典的立体匹配算法，包括基于像素的区域匹配算法、基于特征的匹配算法、基于能量最小化的匹配算法等。

4. 猪体尺参数提取。

通过计算猪体各点的三维坐标，可以得到猪的身高、体长、胸围等参数，并实现对猪体的三维重构。

本文对上述算法进行了优化，主要从以下几个方面入手：1. 图像预处理优化。

本文采用了更加高效的图像去除背景算法，能够准确地将猪体从背景中分离出来。

2. 立体匹配算法优化。

本文采用了基于深度学习的立体匹配算法，在计算视差时能够更加准确地匹配猪体各点之间的对应关系。

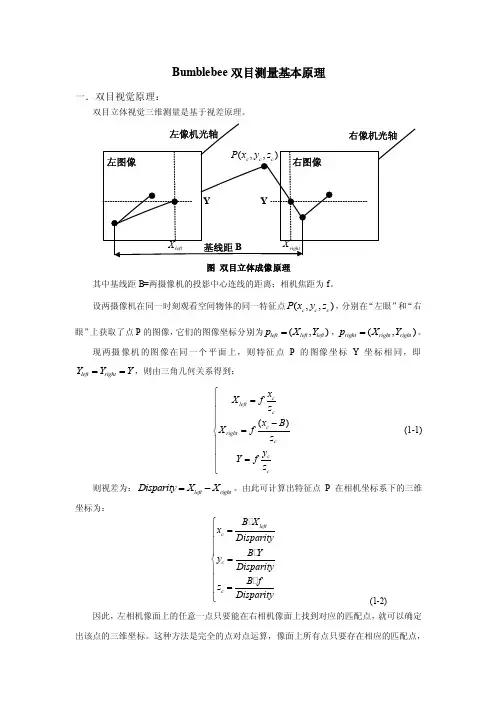
双目视觉基本原理

Bumblebee 双目测量基本原理一．双目视觉原理：双目立体视觉三维测量是基于视差原理。

图 双目立体成像原理其中基线距B=两摄像机的投影中心连线的距离；相机焦距为f 。

设两摄像机在同一时刻观看空间物体的同一特征点(,,)c c c P x y z ，分别在“左眼”和“右眼”上获取了点P 的图像，它们的图像坐标分别为(,)left left left p X Y =，(,)right right right p X Y =。

现两摄像机的图像在同一个平面上，则特征点P 的图像坐标Y 坐标相同，即left right Y Y Y ==，则由三角几何关系得到：()c left c c right c c c x X f z x B X f z y Y f z ⎧=⎪⎪⎪-=⎨⎪⎪=⎪⎩ (1-1)则视差为：left right Disparity X X =-。

由此可计算出特征点P 在相机坐标系下的三维坐标为：left c c c B X x Disparity B Y y Disparity B f z Disparity ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ (1-2)因此，左相机像面上的任意一点只要能在右相机像面上找到对应的匹配点，就可以确定出该点的三维坐标。

这种方法是完全的点对点运算，像面上所有点只要存在相应的匹配点，就可以参与上述运算，从而获取其对应的三维坐标。

二．立体视觉测量过程1．图像获取(1) 单台相机移动获取(2) 双台相机获取：可有不同位置关系（一直线上、一平面上、立体分布）2．相机标定：确定空间坐标系中物体点同它在图像平面上像点之间的对应关系。

(1)内部参数：相机内部几何、光学参数(2)外部参数：相机坐标系与世界坐标系的转换3．图像预处理和特征提取预处理：主要包括图像对比度的增强、随机噪声的去除、滤波和图像的增强、伪彩色处理等；特征提取：常用的匹配特征主要有点状特征、线状特征和区域特征等4．立体匹配：根据对所选特征的计算，建立特征之间的对应关系，将同一个空间物理点在不同图像中的映像点对应起来。

双目测距 步骤、模型建立、特征提取和匹配


3.SIFT尺度不变特征提取：
4）生成特征描述符
首先将坐标轴旋转为特征点的方向，以保证旋转不变性；接下来 以特征点为中心取16×16的窗口（特征点所在的行和列不取）
4.特征匹配：（建立K-D树）
特征匹配算子大致可以分为两类。 一类是线性扫描法，即将数据集中的点与查询点逐一进行距离比 较，也就是穷举，缺点很明显，就是没有利用数据集本身蕴含的任何 结构信息，搜索效率较低。 第二类是建立数据索引，然后再进行快速匹配。因为实际数据一 般都会呈现出簇状的聚类形态，通过设计有效的索引结构可以大大加 快检索的速度。 建立k-d索引树然后用BBF(Best Bin First)算法搜索匹配点属于 第二类。
3.SIFT尺度不变特征提取：
2）精确定位特征点的位置
当然这样产生的极值点并不都是稳定的特征点，因为某些极值点 响应较弱，而且DOG算子会产生较强的边缘响应。通过拟和三维二次 函数以精确确定特征点的位置和尺度（达到亚像素精度），同时可以 去除低对比度的关键点和不稳定的边缘响应点，以增强匹配稳定性、 提高抗噪声能力。
3.SIFT尺度不变特征提取：
3）确定特征点Biblioteka 主方向利用关键点邻域像素的梯度方向分布特性为关键点指定方向参数， 使算子具备旋转不变性。 在以特征点为中心的邻域窗口内采样，并用梯度方向直方图来统 计邻域像素的梯度方向。梯度直方图的范围是0°~360°，其中每10°一 个柱，总共36个柱。梯度方向直方图的峰值则代表了该特征点处邻域 梯度的主方向，即作为该特征点的主方向。在梯度方向直方图中，当 存在另一个相当于主峰值80%能量的峰值时，则将这个方向认为是该 特征点的辅方向。一个特征点可能会被指定具有多个方向（一个主方 向，一个以上辅方向），这可以增强匹配的鲁棒性。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

双目视觉三维重构总结1 照相机成像过程数码照相机的成像过程可通过四个坐标系的三次转换来表达，这四个坐标系分别为：（1）世界坐标系—根据自然环境所选定的坐标系，坐标用（w w w Z Y X ,,）来表示。

（2）光心坐标系（相机坐标系）—以相机的光心O 为坐标原点，c X 轴、c Y 轴分别平行于CCD 平面的两条垂直边，c Z 轴与相机的光轴重合，坐标用（c c c Z Y X ,,）来表示。

（3）图像坐标系—坐标原点l O 在CCD 图像片面的中心，X 轴、Y 轴分别为平行于CCD 平面的两条垂直边，坐标用（x ，y ）表示。

（4）像素坐标系—坐标原点o O 在CCD 图像平面的左上角，U 轴、V 轴分别平行于图像坐标系的X 轴、Y 轴，坐标用（u ，v ）来表示，该坐标值为离散的整数值。

图表 1 数码相机成像坐标系三个转换过程分别是：（1）将世界坐标系中的信息转换到光心坐标系。

（2）光心坐标系中的信息按照针孔模型规律转换到图像坐标系。

（3）最后由图像坐标系转换成像素坐标系。

光学成像的理论模型是针孔模型，根据这个模型，空间任一点P 由光心坐标系向图像坐标系的转换过程符合中心射影或透视投影理论，在图像坐标系中的投影P 可以用光心O 与P 点的连线与图像坐标系平面的交点来表示，数学表达如下：c cz x f x ⋅=ccz y f y ⋅=其中（x,y ）是P 点的图像坐标，（c c c Z Y X ,,）为空间点P 在光心坐标系下的坐标，f 为相机焦距。

可以用齐次坐标与矩阵表示上述中心影射关系：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1010000001cc c c z y x f fy x z 图像坐标系与像素坐标系之间的转换关系如下：0u dxxu +=0v dyyv +=其中dx 、dy 分别是表示CCD 在x 和y 方向的像素点间距。

齐次坐标及矩阵表示如下：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1101001100y x v dy u dx v u逆过程可写成：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110000100v u dy v dy dx u dx y x相机坐标系与世界坐标系之间的关系可以用旋转矩阵R 与平移向量t 来描述，空间中某一点P 在世界坐标系与相机坐标系中的转换关系如下：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1101w w w Tc c c z y x t Rz y x 其中T w w w Z Y X )1,,,(和T c c c Z Y X )1,,,(分别是空间点P 在世界坐标系和相机坐标系中的齐次坐标，R 为33⨯的正交单位矩阵，t 为三维平移向量，T z y x t t t t ),,(=,T )0,0,0(0=为0向量。

由此可以得到以世界坐标系表示的P ),,(w w w Z Y X 点与其投影点P 在像素坐标系中的坐标（u,v ）之间的关系。

⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡11001000000001001001100w w w Tc z y x t R f f v dy u dx v u z ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡11110010000100w w w w w w w w w Ty x c z y x M z y x NH z y x t R v a u a v u z这就是针孔模型下数码相机的成像模型，其中,/,/dy f a dx f a y x ==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=01000000v a u a N y x⎥⎦⎤⎢⎣⎡=10Tt R H N 称之为内部参数矩阵，H 称之为外部参数矩阵，M 为综合矩阵。

2 空间点的三维重构空间点是构成三维空间结构的最基本单元，理论上可以由点形成线，由线形成面，再由各种面构成三维立体结构。

计算机视觉中的三维重构，无论是全像素的重构，还是三维图形的重构，空间点的重构是其最基本的内容。

在许多场合，三维空间结构中有许多特征点，确定了这些特征点的位置，也就能够确定这个三维结构，连接这些特征点就能形成空间结构图形。

假定空间任意点P 的世界坐标为：),,(w w w Z Y X ，点P 在两个相机的成像平面上的像点分别为P1与P2，P1和P2的像素坐标分别为：（u1,v1）和（u2,v2），C1和C2相机的投影矩阵分别为：图表 2 空间点在双相机中的成像关系⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1341331321311241231221211141131121111m m m m m m m m m m m m M⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2342332322312242232222212142132122112m m m m m m m m m m m m M 根据相机的成像模型有：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡11134133132131124123122121114113112111111w w w c z y x m mmm m m m m m m m m v u z⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡11234233232231224223222221214213212211222w w w c z y x m m m m m m m m m m m m v u z 其中zc1和zc2分别为空间点P 在两个相机的光心坐标系中沿光轴方向的坐标值。

展开得到：11411311211111m z m y m x m u z w w w c +++= 12412312212111m z m y m x m v z w w w c +++= 1341331321311m z m y m x m z w w w c +++= 21421321221122m z m y m x m u z w w w c +++= 22422322222122m z m y m x m v z w w w c +++= 2342332322312m z m y m x m z w w w c +++=整理得到：1341114113133111213111111311)()()(m u m z m m u y m m u x m m u w w w -=-+-+- 1341124123133112213111211311)()()(m v m z m m u y m m v x m m v w w w -=-+-+- 2342214213233221223122112312)()()(m u m z m m u y m m u x m m u w w w -=-+-+- 2342224223233222223122212312)()()(m v m z m m v y m m v x m m v w w w -=-+-+-两个线形方程是三维空间的两个平面方程，两个平面方程式的联立为空间直线方程，即为两平面的交线。

实际中，由于在提取已知数据时总是有噪声的影响，这里多数都采用最小二乘法来求解，用矩阵形式表示如下：l Kq =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------------=223233221223222212312213233221213222111312123133112213211211311113133111213211111311m m v m m v m m v m m u m m u m m u m m v m m v m m v m m u m m u m m u K ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=w w w z y x q ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡----=2342224234221413411241341114m v m m u m m v m m u m l l K K K q T T 1)(-=3 对极几何双目配准以及极点求解在双目立体视觉系统中，数据是两个摄像机获得的图像，即左图像和右图像，如果Pa 和Pb 是空间同一点P 在两个图像上的投影点，称为Pa,Pb 为互对应点。

如图所示，Oa,Ob 分别为左右摄像机的透视中心，Oa,Ob 和空间物点P 构成一个平面，城为外极平面。

外极平面与左右像平面的交线Paea 、Pbeb 分别为投影点Pa 、Pb 在左右像平面上的外极线。

OaOb 与左右像平面的交点ea 、eb 叫做左右像平面的极点。

同一像平面上的所有外极线都应相交于e 点，称为像平面的外极中心。

图表 3交向姿态双目视觉模型的对极几何关系对任意一点在世界坐标系，左摄像机坐标系和右摄像机系下的非齐次坐标分别为r l w x x x ,, 由l w l l T x R x += r w r r T x R x += )(1L l l w T x R x -=- r l l r l l r r T T R R x R R x +-=--11可以得到左到右的旋转矩阵和平移矩阵1-=l r R R R l l r r T R R T T 1--=再由l w l l T x R x += r w r r T x R x += )(1r r r w T x R x -=- l r r l r r l l T T R R x R R x +-=--11可以得到右到左的旋转矩阵和平移矩阵1-=r l R R Rr r l l T R R T T 1--=左右摄像机坐标系变换关系 左摄像机到右摄像机的变换关系：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡abz aby abx a a a ab ab ab ab ab ab ab ab ab b b b t t t z y x r r r r r r r r r x x x 987654321 右摄像机到左摄像机的变换关系：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡baz bay bax b b b ba ba ba ba ba ba ba ba ba a a a t t t z y x r r r r r r r r r x x x 987654321右极中心求解⎪⎪⎭⎫⎝⎛⋅⋅b abz aby b abz abx f t t f t t , 左极中心求解⎪⎪⎭⎫ ⎝⎛⋅⋅a baz bay a baz bax f t t f t t , 如果左像平面上一条斜率为ka 并通过左外极中心ea 的直线与右像面上一条斜率为kb 并通过右外极中心eb 直线对应，则这两条直线分别为同一外极平面与左右像平面的交线，它们有如下对应关系：)()()()(21848754b ba ba baz b ba ba bax b ba ba bay b ba ba baz a k r r t k r r t k r r t k r r t k ⨯+-⨯+⨯+-⨯+-= )()()()(21848754a ab ab abz a ab ab abx a ab ab aby a ab ab abz b k r r t k r r t k r r t k r r t k ⨯+-⨯+⨯+-⨯+-=。