QH函数的图像

excel中的qh函数-回复Excel中的qh函数Excel是一款强大的电子表格软件，不仅可以进行数据整理、计算、分析等常见操作，还提供了多种内置函数来帮助用户更高效地进行数据处理。

其中，qh函数是Excel中常用的一个函数，是用于在指定数据区域中查找某个值的函数。

一、qh函数的基本介绍qh函数是Excel中的一个查找函数，其全称为“查询”. 在Excel的函数库中，qh函数是用来在指定区域内查找某个值，并返回该值所在的位置相关信息的函数。

它的基本语法为：qh(查找值，区域，行号，精确匹配/近似匹配)。

具体的参数解释如下：1. 查找值：要在区域内查找的值或者引用；2. 区域：要进行查找的数据区域范围；3. 行号：指定返回结果的行号，通常为1（返回值所在行）、2（返回值所在列）或者0（返回所有相关的位置）；4. 精确匹配/近似匹配：可选参数，表示是否进行精确匹配。

默认为TRUE，表示进行精确匹配；FALSE表示不进行精确匹配。

二、qh函数的使用示例为了更好地理解qh函数的使用方法，下面举例说明：假设我们有一个销售数据表格，其中包含了销售员的姓名、产品名称和销售金额三列。

现在我们想要查找某个销售员的销售金额，以及该金额所在的行号和列号。

首先，我们可以设置一个单元格来输入要查找的销售员姓名，比如A1单元格为"张三"。

然后，在B1单元格中输入以下函数：`=qh(A1,A2:C1000,3)`在这个函数中，我们传入了三个参数：查找值为A1单元格的值（即"张三"），区域为A2:C1000（假设数据表格的范围为A2:C1000），行号为3，表示我们要返回匹配结果所在的行号。

执行该函数之后，我们可以得到查找结果的行号。

为了获取销售金额，我们可以在D1单元格中输入以下函数：`=INDEX(A2:C1000,B1,3)`在这个函数中，我们使用了INDEX函数来根据给定的行号和列号获取相应的数据块。

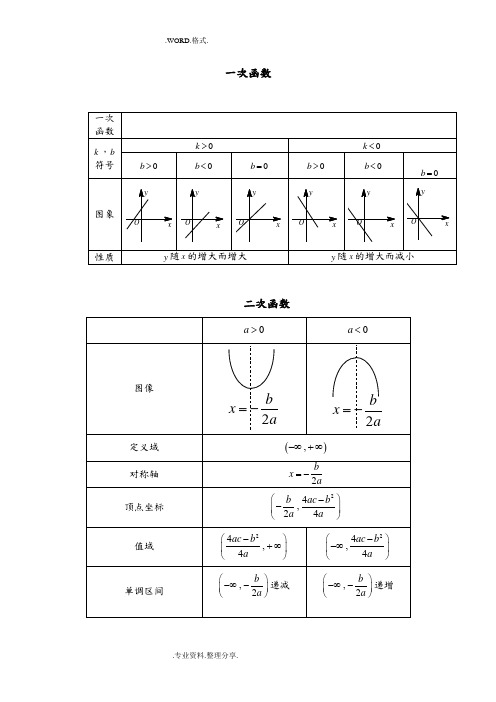
一次函数二次函数反比例函数1、反比例函数图象：反比例函数的图像属于以原点为对称中心的中心对称的双曲线反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交（K≠0）。

2、性质：1.当k>0时，图象分别位于第一、三象限，同一个象限内，y随x的增大而减小；当k<0时，图象分别位于二、四象限，同一个象限内,y随x的增大而增大。

2.k>0时，函数在x<0上同为减函数、在x>0上同为减函数；k<0时，函数在x<0上为增函数、在x>0上同为增函数。

定义域为x≠0；值域为y≠0。

3.因为在y=k/x(k≠0)中，x不能为0，y也不能为0，所以反比例函数的图象不可能与x轴相交，也不可能与y轴相交。

4. 在一个反比例函数图象上任取两点P，Q，过点P，Q分别作x轴，y轴的平行线，与坐标轴围成的矩形面积为S1，S2则S1＝S2=|K|5. 反比例函数的图象既是轴对称图形，又是中心对称图形，它有两条对称轴 y=x y=-x（即第一三，二四象限角平分线），对称中心是坐标原点。

指数函数y=a x (a＞0，a≠1)注意：⒈指数函数对外形要求严格，前系数要为1，否则不能为指数函数。

⒉指数函数的定义仅是形式定义。

指数函数的图像与性质规律：1. 当两个指数函数中的a互为倒数时，两个函数关于y轴对称，但这两个函数都不具有奇偶性。

2.当a＞1时，底数越大，图像上升的越快，在y轴的右侧，图像越靠近y轴；当0＜a＜1时，底数越小，图像下降的越快，在y轴的左侧，图像越靠近y轴。

在y轴右边“底大图高”；在y轴左边“底大图低”。

3.四字口诀：“大增小减”。

即：当a＞1时，图像在R上是增函数；当0＜a＜1时，图像在R上是减函数。

4. 指数函数既不是奇函数也不是偶函数比较幂式大小的方法：1.当底数相同时，则利用指数函数的单调性进行比较；2.当底数中含有字母时要注意分类讨论；3.当底数不同，指数也不同时，则需要引入中间量进行比较；4.对多个数进行比较，可用0或1作为中间量进行比较底数的平移：在指数上加上一个数，图像会向左平移；减去一个数，图像会向右平移。

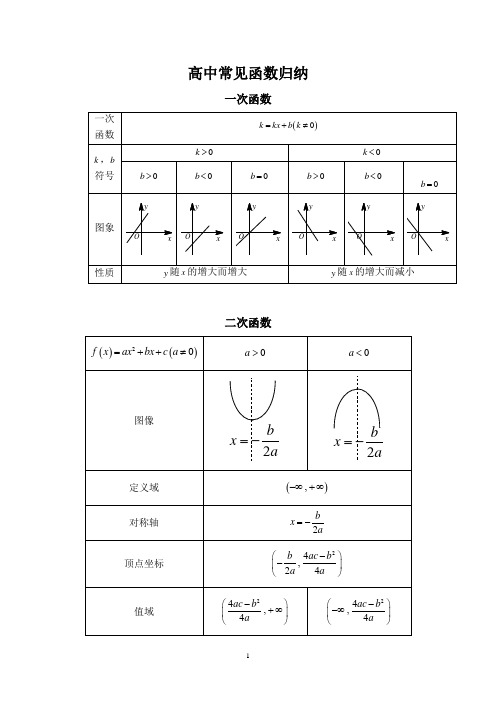
高中常见函数归纳一次函数二次函数单调区间,2ba⎛⎫-∞-⎪⎝⎭递减,2ba⎛⎫-+∞⎪⎝⎭递增,2ba⎛⎫-∞-⎪⎝⎭递增,2ba⎛⎫-+∞⎪⎝⎭递减反比例函数1、反比例函数图象：反比例函数的图像属于以原点为对称中心的中心对称的双曲线指数函数概念：一般地，函数x ay=（a＞0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R。

注意：指数函数对外形要求严格，前系数要为1，否则不能为指数函数。

指数函数的图像与性质规律：1. 当两个指数函数中的a互为倒数时，两个函数关于y轴对称，但这两个函数都不具有奇偶性。

2.当a＞1时，底数越大，图像上升的越快，在y轴的右侧，图像越靠近y轴；当0＜a＜1时，底数越小，图像下降的越快，在y轴的左侧，图像越靠近y轴。

在y轴右边“底大图高”；在y轴左边“底大图低”。

3.四字口诀：“大增小减”。

即：当a＞1时，图像在R上是增函数；当0＜a＜1时，图像在R上是减函数。

4. 指数函数既不是奇函数也不是偶函数比较幂式大小的方法：1.当底数相同时，则利用指数函数的单调性进行比较；2.当底数中含有字母时要注意分类讨论；3.当底数不同，指数也不同时，则需要引入中间量进行比较；4.对多个数进行比较，可用0或1作为中间量进行比较对数函数1.对数函数的概念我们把指数函数y=a x(a＞0，a≠1)的反函数称为对数函数，并记为y=logax(a ＞0，a≠1).因为指数函数y=a x的定义域为(-∞，+∞)，值域为(0，+∞)，所以对数函数y=logax的定义域为(0，+∞)，值域为(-∞，+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数，因此它们的图像对称于直线y=x. 据此即可以画出对数函数的图像，并推知它的性质.为了研究对数函数y=logax(a＞0，a≠1)的性质，我们在同一直角坐标系中作出函数y=log2x，y=log10x，y=log10x,y=log21x,y=log101x的草图图象a＞1 a＜1(1)x＞0比较对数大小的常用方法有：(1)若底数为同一常数，则可由对数函数的单调性直接进行判断.(2)若底数为同一字母，则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同，则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同，则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比幂函数所有幂函数y x α=（x ∈R ，α是常数）的图像都过点)1,1(；对号函数函数xbax y +=（a>0,b>0）叫做对号函数，因其在（0，+∞）的图象似符号“√”而得名，当a b x =时，函数xbax y +=（a>0,b>0,x ∈R +）有最小值a b 2，函数xbax y +=（a>0,b>0）在区间（0，a b ）上是减函数，在区间（a b ，+∞）上是增函数。

常见函数类型的图像分析1. 线性函数线性函数是最简单和常见的函数类型之一，具有形如y = kx + b的表达式。

其中，k表示斜率，决定了函数图像的斜率方向和倾斜程度；b表示截距，决定了函数图像与y轴的截距位置。

当斜率k大于0时，函数图像呈现递增的趋势，即从左下方向右上方逐渐上升；当斜率k小于0时，函数图像呈现递减的趋势，即从左上方向右下方逐渐下降。

截距b代表函数图像与y轴的交点位置，当b大于0时，函数图像在y轴上方与其交点位置较远；当b小于0时，函数图像在y轴下方与其交点位置较远。

2. 二次函数二次函数是一类具有形如y = ax^2 + bx + c的表达式的函数，其中a、b、c为常数，且a不等于0。

二次函数的图像通常为抛物线。

当a大于0时，二次函数的抛物线开口向上，形如"U"的形状；当a小于0时，二次函数的抛物线开口向下，形如"∩"的形状。

抛物线的顶点处为函数的极值点，即最高点或最低点。

通过求解二次函数的导数可以确定极值点的位置。

3. 幂函数幂函数是一类具有形如y = x^n的表达式的函数，其中n为常数。

幂函数的图像形状随着幂数n的不同而变化。

当n大于1时，幂函数呈现递增趋势，随着x的增大，y值也随之增大；当0 < n < 1时，幂函数呈现递减趋势，x值增大，y值减小的速率越来越慢；当n小于0时，幂函数呈现曲线，随着x的增大或减小，y值同样呈现递减趋势。

4. 指数函数指数函数是一类具有形如y = a^x的表达式的函数，其中a为常数且大于0且不等于1。

指数函数的图像通常呈现指数曲线。

当a大于1时，指数函数呈现递增趋势，x值增大，y值也随之增大；当0 < a < 1时，指数函数呈现递减趋势，x值增大，y值减小的速率越来越快。

指数函数的图像还具有特殊的性质，即通过过点(0,1)，可以得到指数函数的对数函数。

5. 对数函数对数函数是指数函数的反函数，具有形如y = log(x)的表达式。

常见函数的图像和性质在数学的世界里，函数就像是一座桥梁，连接着不同的数量关系。

而函数的图像和性质，则是我们理解和把握这些关系的关键。

今天，咱们就来一起聊聊常见函数的图像和性质。

首先，咱们来看看一次函数。

一次函数的表达式一般写作 y ＝ kx＋ b （k、b 为常数，k ≠ 0）。

它的图像是一条直线。

当 k ＞ 0 时，直线是上升的，意味着函数值 y 随着 x 的增大而增大；当 k ＜ 0 时，直线是下降的，函数值 y 随着 x 的增大而减小。

b 呢，则决定了直线与 y轴的交点，当 b ＞ 0 时，交点在 y 轴的正半轴；当 b ＜ 0 时，交点在 y 轴的负半轴；当 b ＝ 0 时，直线过原点。

再来说说反比例函数，它的表达式通常是 y ＝ k ／ x （k 为常数，k ≠ 0）。

反比例函数的图像是两条曲线，叫做双曲线。

当 k ＞ 0 时，双曲线在一、三象限，在每个象限内，y 随 x 的增大而减小；当 k ＜ 0 时，双曲线在二、四象限，在每个象限内，y 随 x 的增大而增大。

二次函数也是常见函数中的重要一员，其表达式一般为 y ＝ ax²＋bx ＋ c （a、b、c 为常数，a ≠ 0）。

二次函数的图像是一条抛物线。

当a ＞ 0 时，抛物线开口向上，有最小值；当 a ＜ 0 时，抛物线开口向下，有最大值。

抛物线的对称轴是直线 x ＝ b ／ 2a 。

而且，判别式Δ ＝ b²4ac 能帮助我们判断抛物线与 x 轴的交点情况。

当Δ ＞ 0 时，抛物线与x 轴有两个交点；当Δ ＝ 0 时，抛物线与 x 轴有一个交点；当Δ ＜ 0 时，抛物线与 x 轴没有交点。

接下来看看指数函数，它的表达式是 y ＝ a^x （a ＞ 0 且a ≠ 1）。

当 a ＞ 1 时，函数单调递增，图像从左到右逐渐上升；当 0 ＜ a ＜ 1 时，函数单调递减，图像从左到右逐渐下降。

指数函数的图像恒过点（0, 1)。

常见函数的图像和性质函数是高中数学学习中不可避免的部分，常见函数有一些图像和性质。

本文将介绍常见函数的图像和性质，包括线性函数、二次函数、指数函数、对数函数和三角函数。

线性函数是最基本的函数之一，也是最容易理解的函数之一。

线性函数的一般式是y = kx + b，其中k和b是常数，x和y表示函数的自变量和因变量。

线性函数的图像是一条直线，斜率k和截距b决定了直线的位置和倾斜程度。

当k>0时，函数是单调递增的，当k<0时，函数是单调递减的。

斜率越大，直线越陡峭，斜率越小，直线越平缓。

截距决定直线和y轴的交点。

当b>0时，直线在y轴上方，当b<0时，直线在y轴下方，当b=0时，直线经过原点。

线性函数的性质是简单的，任何两个不同的点都能确定一条直线，而且任何一条直线都可以写成y = kx + b的形式。

二次函数是另一个基本函数，一般式是y = ax^2 + bx + c，其中a、b、c是常数。

二次函数的图像是一个开口向上或向下的抛物线，抛物线的开口方向由系数a的正负决定。

当a>0时，抛物线开口向上，当a<0时，抛物线开口向下。

二次函数图像的性质和线性函数有所不同，首先，二次函数不是单调函数，也就是说，它有一个最值点，最值点的坐标为（-b/2a，c-b^2/4a）。

第二，二次函数图像的对称轴是一个垂直于x轴的线，它的坐标是x = -b/2a。

第三，二次函数图像上任何一条水平线和抛物线只有一个交点，因此，二次函数也称为单峰函数。

指数函数是一种以底数为e的指数型函数，一般式是y = a^x，其中a是正常数。

指数函数的图像呈现出一种快速增长或快速衰减的趋势，指数函数的性质是独特的。

当a>1时，指数函数单调递增，当0<a<1时，指数函数单调递减，当a=1时，指数函数恒等于1。

指数函数图像的特点是固定的x值下y值呈指数型增长或衰减，在坐标系中的图像表现出“指数型曲线”。

第3章拉格朗日方程以动力学普遍方程为基础，拉格朗日导出了两种形式的动力学方程，分别称为第一类和第二类拉格朗日方程。

将达朗贝尔原理与虚位移原理相结合，建立起动力学普遍方程，避免了理想约束力的出现；再把普遍方程变为广义坐标形式，进一步转变为能量形式，导出了第二类拉格朗日方程，实现了用最少数目的方程描述动力系统；应用数学分析中的乘子法，采用直角坐标形式的普遍方程和约束方程而建立的一组动力学方程，是第一类拉格朗日方程，便于程式化处理约束动力系统问题。

拉格朗日方程是分析力学得以发展之源。

3.1 第二类拉格朗日方程第二类拉格朗日方程是分析力学中最重要的动力学方程，它给出动力学问题一个普遍、简单而又统一的解法。

拉格朗日方程只适用于完整约束的质点系。

3.1.1 几个关系式的推证为方便起见，在推导拉格朗日方程前，先推证几个关系式。

质点系由n个质点、s个完整的理想约束组成，它的自由度数为k＝3n–s，广义坐标数与自由度数相等。

该系统中，任一质点M i的矢径r i可表示成广义坐标q1，q2，…，q k和时间t的函数，即r i＝r i(q1，q2，…，q k，t)i＝1,2,…,n它的速度(3-1)i＝1,2,…,n式中称为h个广义坐标的广义速度，分别为广义坐标和时间的函数，与广义速度没有直接的关系。

式(3-1)对求偏导数，则有(3-2)这是推证的第一个关系式，它表明，任一质点的速度对广义速度的偏导数等于其矢径对广义坐标的偏导数。

为推证第二个关系式，将式(3-1)对广义坐标q j求偏导数，或(3-3)这是第二个关系式，它表明，任一质点的速度对广义坐标的偏导数等于其矢径对广义坐标的偏导数，再对时间的一阶导数。

再看看质点的动能对广义坐标的偏导数。

有(A)又式(3-2)、式(3-3)代入上式，并注意式(A)的关系，(3-4)3.1.2 第二类拉格朗日方程动力学普遍方程可以改写为(3-5)左侧的第一项主动力的虚功之和，可以用广义力Q h在广义虚位移q h上所做的功之和表示，即(3-6)值得指出，这里的主动力并非平衡问题中的主动力，因此，这里的广义力Q h不等于零。

一元二次函数的图象和性质(-)二次函数基本知识1.二次函数的定义：形如y = 加+ C(QH O且为常数)的函数叫关于X的二次函数。

2.二次函数的解析式的三种形式(1)-般式(三点式)：y = ax2+bx + c(a^O)f配方后为_____________________________ 。

其中顶点坐标为___________ ，对称轴为__________ 0(2)顶点式(配方式)：y = a(x-h)2+k(a^o)f其中顶点坐标为_______________ ,对称轴为_______(3)两根式(零点式)：y = a(x-x])(x-x2)(a^o),其中西‘吃是方程+Z?x + c = 0的两个根，同时也是二次函数的图像与兀轴交点(召,0),(花,0)的横坐标。

求函数解析式时，一般采用待定系数法3 •二次函数的图像和性质(1)二次函数y = ax2+bx + c(a^0)的图像是一条___________ ,其对称轴为_________ ,顶点坐标为 ________ ,开口方向由_____ 决定。

(2)二次函数y = ox? + bx + C(G H 0)的单调性以对称轴为分界。

在作二次函数草图时，往往抓住：开口方向，对称轴，与X轴交点，与『轴交点，顶点等。

(3)二次幣数y二处2+b兀+C(QH0),当△ = /?? _4QC>0时，图像与兀轴有两个交点M}(x,,0),,0),则\M^\=\X2-X\= J(血 + 西)2一4无內=J(--)2-4 -=血—仏_ _ \ a a \a\(4)关于二次函数y = /(x)的对称轴的判断方法：①若二次函数对定义域内所有兀，都有/(Xj) = /(X2),则其对称轴为兀二西[尢2②若二次函数对定义域内所有无，都有f(m+x) = f(m-x)1则其对称轴为x=m.4ac-b 24a(2)在闭区I 可n ］上的最值“轴变区间定” w + n③ 若二次函数对定义域内所有x,都有f(m+x) = f(n-x),则对称轴为% =——④.若二次函数对应方程为/(X)= 0两根为知兀2,则对称轴方程为：x =—---------二24.二次函数y = ax 2+bx+c(a^O)的最值 (1) 在(Y0,+00)上的最值二次函数加+C @H O)在闭区间［弘切上的最值问题，一般情况下，需要分三种情况讨论，依据对称轴与区间的位置关系：唸5,心存〃冷九再结合图像分析。

一次函数（一）函数1、确定函数定义域的方法：（1）关系式为整式时，函数定义域为全体实数； （2）关系式含有分式时，分式的分母不等于零； （3）关系式含有二次根式时，被开放方数大于等于零； （4）关系式中含有指数为零的式子时，底数不等于零；（5）实际问题中，函数定义域还要和实际情况相符合，使之有意义。

（二）一次函数1、一次函数的定义一般地，形如y kx b =+（k ，b 是常数，且0k ≠）的函数，叫做一次函数，其中x 是自变量。

当0b =时，一次函数y kx =，又叫做正比例函数。

⑴一次函数的解析式的形式是y kx b =+，要判断一个函数是否是一次函数，就是判断是否能化成以上形式．⑵当0b =，0k ≠时，y kx =仍是一次函数． ⑶当0b =，0k =时，它不是一次函数．⑷正比例函数是一次函数的特例，一次函数包括正比例函数．2、正比例函数及性质一般地，形如y=kx(k 是常数，k ≠0)的函数叫做正比例函数，其中k 叫做比例系数. 注：正比例函数一般形式 y=kx (k 不为零) ① k 不为零 ② x 指数为1 ③ b 取零当k>0时，直线y=kx 经过三、一象限，从左向右上升，即随x 的增大y 也增大；当k<0时，•直线y=kx 经过二、四象限，从左向右下降，即随x 增大y 反而减小．(1) 解析式：y=kx （k 是常数，k ≠0）(2) 必过点：（0，0）、（1，k ）(3) 走向：k>0时，图像经过一、三象限；k<0时，•图像经过二、四象限(4) 增减性：k>0，y 随x 的增大而增大；k<0，y 随x 增大而减小(5) 倾斜度：|k|越大，越接近y 轴；|k|越小，越接近x 轴3、一次函数及性质一般地，形如y=kx ＋b(k,b 是常数，k ≠0)，那么y 叫做x 的一次函数.当b=0时，y=kx ＋b 即y=kx ，所以说正比例函数是一种特殊的一次函数.注：一次函数一般形式 y=kx+b (k 不为零) ① k 不为零 ②x 指数为1 ③ b 取任意实数一次函数y=kx+b 的图象是经过（0，b ）和（-kb，0）两点的一条直线，我们称它为直线y=kx+b,它可以看作由直线y=kx 平移|b|个单位长度得到.（当b>0时，向上平移；当b<0时，向下平移）（1）解析式：y=kx+b(k 、b 是常数，k ≠0) （2）必过点：（0，b ）和（-kb，0） （3）走向： k>0，图象经过第一、三象限；k<0，图象经过第二、四象限 b>0，图象经过第一、二象限；b<0，图象经过第三、四象限⇔⎩⎨⎧>>00b k 直线经过第一、二、三象限 ⇔⎩⎨⎧<>00b k 直线经过第一、三、四象限 ⇔⎩⎨⎧><0b k 直线经过第一、二、四象限 ⇔⎩⎨⎧<<0b k 直线经过第二、三、四象限（4）增减性： k>0，y 随x 的增大而增大；k<0，y 随x 增大而减小.（5）倾斜度：|k|越大，图象越接近于y 轴；|k|越小，图象越接近于x 轴.（6）图像的平移： 当b>0时，将直线y=kx 的图象向上平移b 个单位；当b<0时，将直线y=kx 的图象向下平移b 个单位.4、一次函数y=kx＋b的图象的画法.根据几何知识：经过两点能画出一条直线，并且只能画出一条直线，即两点确定一条直线，所以画一次函数的图象时，只要先描出两点，再连成直线即可.一般情况下：是先选取它与两坐标轴的交点：（0，b），.即横坐标或纵坐标为0的点.5、正比例函数与一次函数之间的关系一次函数y=kx＋b的图象是一条直线，它可以看作是由直线y=kx平移|b|个单位长度而得到（当b>0时，向上平移；当b<0时，向下平移）6、正比例函数和一次函数及性质6、直线11b x k y +=（01≠k ）与22b x k y +=（02≠k ）的位置关系 （1）两直线平行⇔21k k =且21b b ≠ （2）两直线相交⇔21k k ≠（3）两直线重合⇔21k k =且21b b = （4）两直线垂直⇔121-=k k7、用待定系数法确定函数解析式的一般步骤：（1）根据已知条件写出含有待定系数的函数关系式；（2）将x 、y 的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程；（3）解方程得出未知系数的值；（4）将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.8、一元一次方程与一次函数的关系任何一元一次方程到可以转化为ax+b=0（a ，b 为常数，a ≠0）的形式，所以解一元一次方程可以转化为：当某个一次函数的值为0时，求相应的自变量的值. 从图象上看，相当于已知直线y=ax+b 确定它与x 轴的交点的横坐标的值.9、一次函数与一元一次不等式的关系任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0（a ，b 为常数，a ≠0）的形式，所以解一元一次不等式可以看作：当一次函数值大（小）于0时，求自变量的取值范围.10、一次函数与二元一次方程组（1）以二元一次方程ax+by=c 的解为坐标的点组成的图象与一次函数y=bcx b a +-的图象相同.（2）二元一次方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解可以看作是两个一次函数y=1111b cx b a +-和y=2222b cx b a +-的图象交点.二次函数一、二次函数概念：1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

函数名 一次函数二次函数反比例函数指数函数 解析式)0()(≠+=a b ax x f )0()(≠=k xkx f 图像定义域 R R {}0|≠x xR值域 R），（∞+0 必过点）（b ,0），（c 0 )1,(1,--k k ）（）（1,0 周期性 不是周期函数 不是周期函数 不是周期函数不是周期函数单调性在R 上单增)2-a b-∞，（为减),2+∞-ab （为增 ）为减，（0-∞）为减，（∞+0为减为增，101<<>a a最值在R 不存在最大最小值 开口向上有最小值ab ac y 442min-=不存在最大最小值在R 上不存在最大最小值奇偶性非奇非偶函数为奇函数00≠=b b偶函数为非奇非为偶函数，00≠=b b 奇函数 非奇非偶函数对称性为常数。

对称，函数图像关于直线任何一点对称；关于图像上t t x a y +=1-对称直线函数图像关于abx 2-= 图像关于原点对称；对称。

直线关于对称；直线图像关于x y x y -== 既不成中心对称也不成轴对称。

渐近线无 无.00==y x 直线或者直线.0=y 直线)0()(2≠++=a cbx ax x f )10()(≠=a a a x f x且＞0＞a 0＞a 0＞k ),44[2+∞-abac ），（），（∞+⋃∞00-a y =)10(<<a xa y =)1(>a xyO1函数名 对数函数幂函数 双钩函数 含绝对值函数解析式)10(log ≠>=a a y xa且Y=x a 如)0(≥=x xyba b x a x y <-+-=设为了研究方便图像O 1yx)10(log <<=a y xa)1(log >=a y xa定义域 ()∞+，0[)∞+，00}x |{x ≠R值域R[)∞+，0(][)∞+∞，，ab ab 22--[)+∞-,a b必过点）（0,1()1,1)2,(2,ab abab ab--）（),(,a b b a b a --）（周期性 不是周期函数 不是周期函数 不是周期函数 不是周期函数单调性单调递减。