第二章作业
- 格式:doc
- 大小:27.50 KB
- 文档页数:1

第二章作业一、单项选择题1、通常以( C )代表时间价值率。
A、通货膨胀补偿率B、风险报酬率C、利息率D、投资利润率2、财务管理的两个基本价值观念是( A )A、时间价值和风险收益B、利润和成本C、风险和利润D、时间价值和成本3、在存本付息的情况下,若想每年都得到利息1000,利率为5%,则现在应存入的本金应为( A )元。
(永续年金的计算问题)A、20000B、50000C、500000D、2000004、一定时期内连续发生在期末的等额支付款项,被称为( B )A、先付年金B、普通年金C、永续年金D、延期年金5、下面有关资金时间价值的表述,正确的是( A )A.资金时间价值的实质是资金周转使用后的增值额B.资金时间价值是推迟消费所获得的报酬C.资金时间价值只能用绝对数来表示D.资金时间价值的量无法进行计量(选择A,严格将来,时间价值是资金周转增值额的一部分,但是因为题目中没有使用“全部”的字样,可以理解为正确;B推迟消费获得的报酬不一定能获得报酬,比如资金不周转的情形。
)6、一项借款,期限一年,年利率8%,按复利计算每半年复利一次,则借款实际利率为( D )A、0.16%B、12.49%C、18.53%D、8.16%(已知名义利率求实际利率的情形)7、永续年金具有下列特征( C )A、每期期初支付B、每期不等额支付C、没有终值D、没有现值8、资金时间价值实质是( B )。
A、资金的自然增值B、资金周转使用后的增值C、不同时间的价值量D、对暂缓消费的报酬9、为在第三年末获得本利和100元,求每年末存入多少资金,计算时应采用(B)。
A、年金现值系数B、年金终值系数C、复利现值系数D、复利终值系数(100元是终值,所以用终值系数计算)10.每年年底存款100元,求第5年末的价值,可用( D )来计算.(终值计算问题)A.PVIF i,n B.FVIF i,n C. PVIFA i,n D.FVIFA i,n11、当利率为10%,计息期为5时,后付年金现值系数为3.791;计息期为6时,后付年金现值系数为4.355,那么利率为10%。
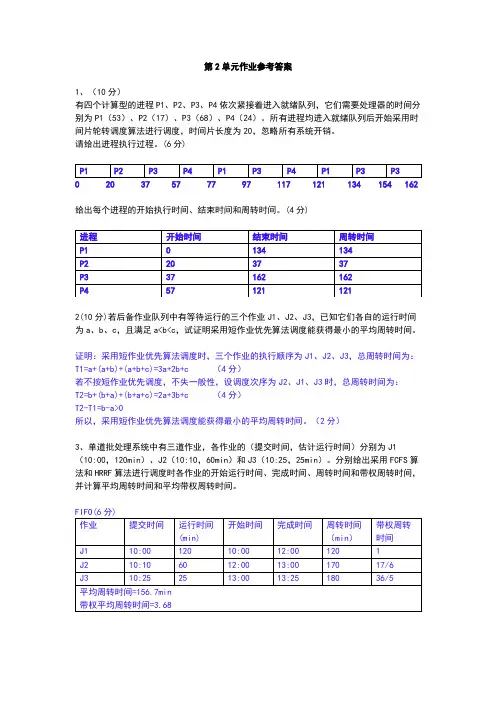
13简答题:简述处理机管理的主要功能。
进程控制和管理;⑵进程同步和互斥;⑶进程通信;⑷进程死锁;⑸线程控制和管理;⑹处理器调度。
(每条1分,总分4分)14简答题:简述中断和异常的区别中断是由与现行指令无关的中断信号触发的(异步的),且中断的发生与CPU处在用户模式或内核模式无关,在两条机器指令之间才可响应中断;异常是由处理器正在执行现行指令而引起的,一条指令执行期间允许响应异常。
(1分)⑵中断处理程序处理过程中是不能阻塞的,异常处理程序处理过程中是可以阻塞的。
(1分)⑶中断允许发生嵌套,但异常大多为一重。
(1分)异常处理过程中可能会产生中断,但中断处理过程中决不会被异常打断。
(1分)15简述进程的主要属性。
(1)动态性:有一定的生命周期⑵共享性:多个进程可执行同一程序,进程可以共享公共资源⑶独立性:是一个独立实体,有自己的虚存空间、程序计数器和内部状态,是资源分配、保护和调度的基本单位⑷制约性:存在制约关系(5)并发性:执行时间上会有所重叠16(每条1分,总分4分)16简答题:简述引起进程状态转换的具体原因。
(1)运行态→等待态:等待使用资源或某事件发生;(1分)⑵等待态→就绪态:资源得到满足或事件发生;(1分)⑶运行态→就绪态:运行时间片到;出现有更高优先权进程;(1分)⑷就绪态→运行态:CPU空闲时选择一个就绪进程。
(1分)17、简答题:进程的基本状态有哪些?请画出进程的状态转换图。
进程的基本状态包括:就绪态、运行态和等待态;(2分)⑵进程的状态转换图如下:(2分)18、简答题:简述进程映象的要素。
(1)进程控制块:标志信息、现场信息、控制信息;(1分)⑵进程核心栈:中断/异常现场、函数调用的参数和返回地址;(1分)⑶进程程序块:进程执行的程序;(1分)⑷进程数据块:私有地址空间,私有数据、用户栈。
(1分)19、简答题:简述引起进程调度的原因。
(1)进程终止⑵进程阻塞⑶进程时间片用完经,⑷进程创建⑸进程请求I/O操作完成⑹进程优先级改变⑺进程运行过程中发生中断或异常⑻进程执行系统调用(每条1分,总分4分)20、下列指令中,哪些是特权指令?⑴关中断;⑵访管指令;⑶设置系统时钟;⑷移位指令;⑸启动I/O;⑹读时钟日期;⑺控制中断屏蔽位(1)、⑶、⑸、⑺(每答对1个得1分,答错1个扣1分)。


第二章作业2、画前驱图4、程序并发执行时为什么会失去封闭性和可再现性?答:程序在并发执行时,是多个程序共享系统中的各种资源,因而这些资源的状态将由多个程序分别来改变,致使程序的运行换去了封闭性,这样,某程序在执行时,必然会受到其它程序的影响。
程序在并发执行时,由于失去了封闭性,也将导致其再失去可再现性。
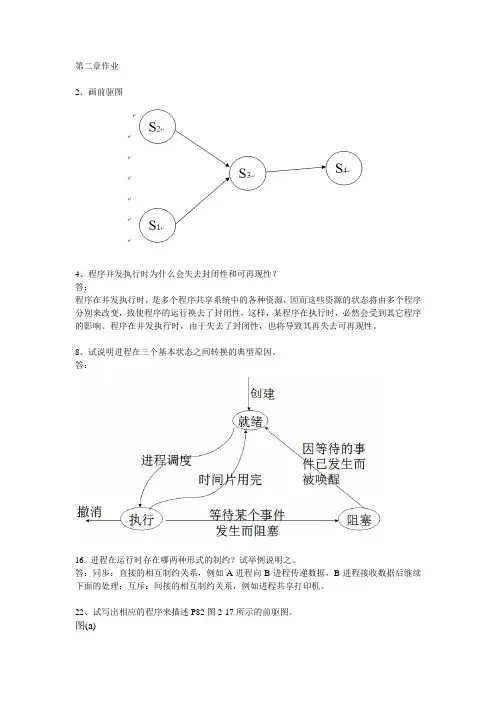
8、试说明进程在三个基本状态之间转换的典型原因。
答:16. 进程在运行时存在哪两种形式的制约?试举例说明之。
答:同步:直接的相互制约关系,例如A进程向B进程传递数据,B进程接收数据后继续下面的处理;互斥:间接的相互制约关系,例如进程共享打印机。
22、试写出相应的程序来描述P82图2-17所示的前驱图。
图(a)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);end;begin P(a3);S4;V(a6);end;begin P(a4);S5;V(a7);end;begin P(a5);S6;V(a8);end;begin P(a6);P(a7);P(a8);S7;end;parend图(b)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;a9=0;a10=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);V(a6);end;begin P(a3);S4;V(a7);end;begin P(a4);S5;V(a8);end;begin P(a5);S6;V(a9);end;begin P(a6);S7;V(a10);end;begin P(a7);P(a8);P(a9);P(a10);S8;end;parend28、在测量控制系统中的数据采集任务,把所采集的数据送一单缓冲区;计算任务从该单缓冲中取出数据进行计算。


第二章 力学一.选择题1【基础训练4】、如图2-14,物体A 、B 质量相同,B 在光滑水平桌面上.滑轮与绳的质量以及空气阻力均不计,滑轮与其轴之间的摩擦也不计.系统无初速地释放,则物体A 下落的加速度是 (A) g. (B) 4g /5 . (C) g /2 . (D) g /3 .,,42,/2,.5b b b a a a b a b a a T m a m g T ma g T T a a a =-==== 2【自测1】、在升降机天花板上拴有轻绳,其下端系一重物,当升降机以加速度a 1上升时,绳中的张力正好等于绳子所能承受的最大张力的一半,问升降机以多大加速度上升时,绳子刚好被拉断(A) 2a 1. (B) 2(a 1+g ).(C) 2a 1+g . (D) a 1+g .[C ]1max max 122T mg ma m a a ma T T T mg maa a g -==+==-==+物对地物对机机对地()3【自测2】、质量为m 的小球,放在光滑的木板和光滑的墙壁之间,并保持平衡,如图2-22所示.设木板和墙壁之间的夹角为,当逐渐增大时,小球对木板的压力将 (A) 增加. (B) 减少. (C) 不变.(D) 先是增加,后又减小.压力增减的分界角为=45°.αm图2-22BA【解答】受力分析如图右所示:垂直于板面的压力sin /sin N mg N mg αα=→=4【自测3】、两个质量相等的小球由一轻弹簧相连接,再用一细绳悬挂于天花板上,处于静止状态,如图2-23所示.将绳子剪断的瞬间,球1和球2的加速度分别为(A) a 1=g,a 2=g. (B) a 1=0,a 2=g. (C) a 1=g,a 2=0. (D) a 1=2g,a 2=0[D ]121211200020T m g F F m g m m F mgT mg F ma a g a --=-====→--==-=弹弹弹弹,(负号表示向下)5【附录A3】.一根细绳跨过一光滑的定滑轮,一端挂一质量为M 的物体,另一端被人用双手拉着,人的质量M m 21=.若人相对于绳以加速度a 0向上爬,则人相对于地面的加速度(以竖直向上为正)是(A) 3/)2(0g a +. (B ) )3(0a g --.图2-23(C3/)2(0g a +- (D)0a()()()()3/2,3/,)(00000a g a a a g a ma a m M g m M a a m mg T MaT Mg +=+∴-=++=-+=-=-二、填空题6【基础训练9】、 质量为m 的小球,用轻绳AB 、BC 连接,如图2-18,其中AB 水平.剪断绳AB 前后的瞬间,绳BC 中的张力比 T : T ′= .A7【自测9】质量分别为m 1、m 2、m 3的三个物体A 、B 、C ,用一根细绳和两根轻弹簧连接并悬于固定点O ,如图2-27.取向下为x 轴正向,开始时系统处于平衡状态,后将细绳剪断,则在刚剪断瞬时,物体B 的加速度B a ϖ=_______;物体A 的加速度A a ϖ=______.()g m m a a g m f g m a m f mg f f g m m B A ab B a ab ab3232232-.0,--.,=====+=+断后,未断时,8【自测10】、一小珠可以在半径为R 的竖直圆环上作无摩擦滑动,如图2-28.今使圆环以角速度绕圆环竖直直径转动.要使小珠离开环的底部停在环上某一点,则角速度最小应大于_____gR________.22min cos sin sin ,cos N mg N m R g gg R RRθθωθωωθ==∴=>∴>三、计算题9【基础训练12】、水平转台上放置一质量M =2 kg 的小物块,物块与转台间的静摩擦系数μs =,一条光滑的绳子一端系在物块上,另一端则由转台中心处的小孔穿下并悬一质量m =0.8 kg 的物块.转台以角速度ω=4 rad/s 绕竖直中心轴转动,求:转台上面的物块与转台相对静止时,物块转动半径的最大值r max 和最小值r min .O x A B Cm 1 m 2m 3ORO图2-28AB?10【自测12】、质量为m 的小球,在水中受的浮力为常力F ,当它从静止开始沉降时,受到水的粘滞阻力大小为f =kv (k 为常数).证明小球在水中竖直沉降的速度v 与时间t 的关系为),e 1(/m kt kFmg ---=v 式中t 为从沉降开始计算的时间。

第二章作业题学号姓名2-4、在杨氏实验装置中,光源波长为0.64m,两缝间距为0.4mm,光屏离缝的距离为50cm。
(1)试求光屏上第一亮条纹与中央亮条纹之间的距离;(2)若P 点离中央亮条纹为0.1mm,则两束光在P 点的相位差是多少?(3)求P 点的光强度和中央点的光强度之比。
2-5、在杨氏实验装置中,两小孔的间距为0.5mm,光屏离小孔的距离为50cm。
当以折射率为1.60 的透明薄片贴住小孔S2 时,发现屏上的条纹移动了1cm,试确定该薄片的厚度。
2-6、在双缝实验中,缝间距为0.45mm,观察屏离缝115cm,现用读数显微镜测得l0 个干涉条纹(准确说是11 个亮条或暗条)之间的距离为15mm,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-7、一波长为0.55m 的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝间距增加到2mm,条纹间距又是多少?2-9、试求能产生红光(=0.7m)的二级反射干涉条纹的肥皂薄膜厚度。
已知肥皂膜的折射率为1.33,且平行光与法向成300 角入射。
2-10、波长为0.40~0.76m 的可见光正入射在一块厚度为1.2×10-6m、折射率为1.5 的落玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-12、如图所示的尖劈形薄膜,右端厚度h=0.005cm,折射率n=1.5,波长为0.707m 的光以300 角入射到上表面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-13、如图所示,平板玻璃由两部分组成(冕牌玻璃n=1.50,火石玻璃n=1.75),平凸透镜用冕牌玻璃制成,其间隙充满二硫化碳(n=1.62),这时牛顿环是何形状?2-15、在观察牛顿环时,用1=0.5m 的第6 个亮环与用 2 的第7 个亮环重合,求波长2=?2-16、平行平面玻璃板的厚度h0 为0.1cm,折射率为1.5,在λ为0.6328µm 的单色光中观察干涉条纹。

第二章 《随机变量及其分布》作业班级 学号 姓名一、单项选择题1. 设连续随机变量X 的概率密度为⎪⎩⎪⎨⎧<<=其它,;,020,2)(x x x f 则P {-3≤X ≤1}= ( ) (A). 0(B). 0.25(C). 0.5(D). 12.设随机变量X 服从参数为λ的泊松分布,且{}{}21===X P X P , 则λ=( )(A) 1 ; (B) 2 ; (C) 3; (D) 4. 3.设随机变量),(~2σμN X ,则=≤≤)(b X a P ( )).(A )()(b a Φ-Φ; ).(B )()(b a Φ+Φ; ).(C )()(σμσμ-Φ--Φb a ; ).(D )()(σμσμ-Φ--Φa b .4. 若4重伯努利试验中,事件A 至少发生一次的概率为8165,则在一次 试验中,事件A 发生的概率为( )).(A 1; ).(B 32; ).(C 41; ).(D 43.5. 设随机变量,且,则c=( ).0 ; ; ; .二 .填空题1.已知随机变量只能取-1,0,1,2四个数值,其相应的概率依次是,则2.则X 的分布函数为=)(x F .),(~2σμN X )()(c X p c X p >=≤)(A )(B μ)(C μ-)(D σX c c c c 161,81,41,21=c3.设连续型随机变量X 的概率密度为⎪⎩⎪⎨⎧≤<-≤≤=其它021)2(10)(x x k x kx x f ,则k= ; ⎭⎬⎫⎩⎨⎧≤≤2321X P = .4.某高速公路一天的事故数X 服从参数3=λ的泊松分布,则一天内没有发生事故的概率是5.设离散型随机变量X 的分布列为则 随机变量函数 Y =()21+X 的分布列是6.设随机变量ξ在(1,6)上服从均匀分布,求方程012=++x x ξ有实根的概率 .7.已知ξ服从)4,150(2N ,则140(P <=≤)160ξ ,=≤)150(ξP 。
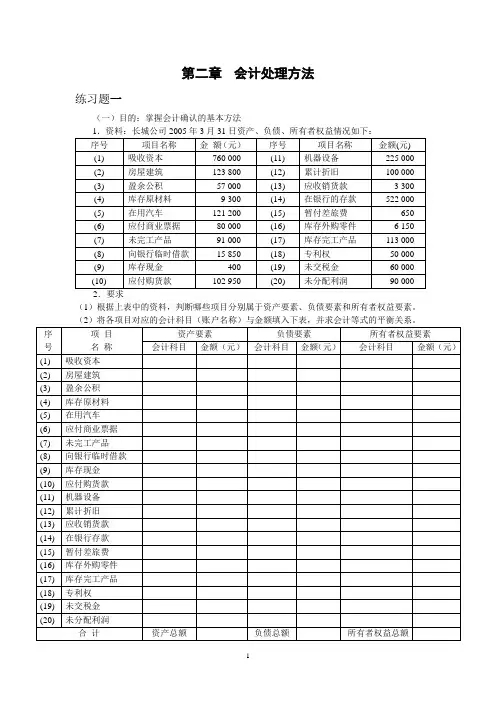
第二章会计处理方法练习题一(一)目的:掌握会计确认的基本方法(1)根据上表中的资料,判断哪些项目分别属于资产要素、负债要素和所有者权益要素。
练习题一参考答案要点(1)资产要素的有:(2);(4);(5);(7);(9);(11);(12);(13);(14);(15);(16);(17);(18) 负债要素的有:(6);(8);(10);(19)所有者权益要素的有:(1);(3);(20)(2)负债表存货项目中。
严格来说,此处是不对的。
因为“生产成本”是费用类账户。
练习题二(二)目的:掌握权责发生制与收付实现制1.资料绿叶公司2005年10月份发生如下经济业务:(1)支付本月的水电费300元。
(2)预付下个月房屋租金2 000元。
(3)支付上月工商部门罚款500元。
(4)销售商品收入20 000元,款项尚未收到。
(5)支付上月购货款38 000元。
(6)采购员报销差旅费2 500元,退回多余现金500元(出差前预借3 000元)。
(7)收到上月销售货款500 000,存入银行。
2.要求分别根据权责发生制和现金收付制,确认和计算本月收入与费用(将结果填入下表)。
练习题二参考答案要点练习题三(三)目的:掌握会计确认的基本方法1.资料上扬公司2005年12月发生如下经济交易与事项:(1)10日,与甲公司签订购货合同,协议购买A材料50万元,约定合同签订之日起10日内预付购货定金10万元。
(2)12日,有一批产品完工验收入库,这批产品的生产成本为20万元。
(3)18日,根据购货合同预付甲公司购货定金10万元。
(4)20日,公司发生失窃事件,丢失现金5万元。
(5)25日,以银行存款预付下年度财产保险费3万元。
(6)28日,以银行存款支付本季度贷款利息费用9万元,其中前两个月已预提6万元。
(7)31日,计算出本月产品销售应缴纳的税金5万元,但尚未实际缴纳。
(8)31日,计算出本月应负担的工资费用15万元,其中管理人员5万元,生产工人10万元,公司每月的工资在下月上旬发放。
第2章习题一、是非题(错误需说明理由)1.由于分子间相互作用力的存在,实际气体的摩尔体积一定小于同温同压下的理想气体的摩尔体积,所以,理想气体的压缩因子Z=1,实际气体的压缩因子Z<1。
(错,因为实际气体的Z可能大于1,也可能等于1,也可能小于1)2.纯物质由蒸气变成固体,必须经过液相。
(错,可以直接变成固体)3.气体混合物的virial系数,如B,C …,是温度和组成的函数。
(对)4.三参数对应态原理较两参数对应态原理优秀,因为前者适合于所有流体。
(错,三参数对应态原理不能适用于任何流体,一般能用于正常流体)5.在压力趋近于零的极限条件下,所有的流体将成为简单流体。
(错,简单流体系指一类非极性的球形流体,如Ar等,与所处的状态无关)6.压力低于所处温度下的饱和蒸气压的液体称为过热液体。
(对)7.压力高于同温度下的饱和蒸气压的气体称为过冷蒸气。
(对)二、选择题1.T温度下的过冷纯液体的压力P(A )A >p s(T) B< p s(T) C = p s(T)2.T温度下的过热纯蒸汽的压力P(B)A >p s(T) B< p s(T) C = p s(T)3.指定温度下的纯物质,当压力大于该温度下的饱和蒸气压时,该物质的状态为:(B)A 饱和蒸气B 超临界流体C 过热蒸气D压缩液体4.偏心因子是从下列定义的(C)A 分子的对称性B 蒸气压性质C 分子的极性5.纯物质的第二维里系数B (A)A 仅是T的函数B 是T和p的函数C 是T和V的函数D 是任何两个强度性质的函数6.真实气体在( D )的条件下,其行为与理想气体相近。
A高温高压B低温低压 C 低温高压 D 高温低压三、填空题(如有计算部分,需按计算题处理:分布列式说明)纯物质的临界等温线在临界点的斜率和曲率均为零,在数学上可以表示为1.和。
2.对于纯物质,一定温度下的泡点压力与露点压力是相同的(相同/不同);一定温度下的泡点与露点,在p-T图上是重叠的(重叠/分开),而在p-V图上是分开的(重叠/分开),泡点的轨迹称为饱和液相线,露点的轨迹称为饱和汽相线,饱和气、液相线与三相线所包围的区域称为汽液共存区。
第⼆章作业参考答案第⼆章1.请分别画出⼆进制⽐特流01001011的NRZ、Manchester和Difference Manchester编码。
约定:对于不归零码低电平代表0,⾼电平代表1;对于曼彻斯特编码由⾼到低电平的跳变代表0,从低到⾼电平的跳变代表1;对于差分曼彻斯特编码每位开始有跳变代表0,反之代表1。
2.数字数据的模拟信号编码中数字调制的三种基本形式。
移幅键控法ASK、移频键控法FSK、移相键控法PSK3.PCM的步骤及⽅法PCM的典型应⽤就是语⾳数字化。
PCM主要包括:采样、量化、编码。
采样:以采样定理为基础,对连续变化的模拟信号进⾏周期性采样,利⽤有限个采样值代替连续变化的模拟信号。
只要采样频率⼤于等于有效信号最⾼频率或其带宽的⼆倍,则采样值便可包含原始信号的全部信息,利⽤低通滤波器可以从这些采样中重新构造出原始信号。
量化:使连续模拟信号变为时间轴上的离散值,将采样样本按照量化级取值。
编码:将离散值变成⼀定位数的⼆进制数码。
量化级越多,量化精度越⾼,需要的⼆进制位数越多。
4.什么是⽐特同步和帧同步?什么是同步通信和异步通信,⼆者的区别是什么?⽐特同步⼜叫位同步,是数据通信中最基本的同步⽅式。
⽐特同步是指接收端将时钟调整到和发送端完全⼀样,当接收到⽐特流后,在正确的时刻对收到的信号根据事先已约定好的规则进⾏判决,从⽽将发送端发送的每⼀个⽐特都正确地接收下来。
(正确时刻:通常就是在每⼀个⽐特的中间位置判决规则:如,电平若超过⼀定数值则为1,否则为0)。
数据通常以帧为单位进⾏发送。
帧同步是指接收端应当能从收到的⽐特流中准确地区分出⼀帧的开始和结束的位置。
帧同步⼜叫帧定界。
同步通信是每发送完⼀个帧进⾏⼀次同步。
这个帧中通常含多个字符、多个字节或不定长的较多的⽐特,即同步通信中⼀次传输的数据量⼀般⽐较⼤。
同步通信要求发送时钟与接收时钟应保持完全⼀致,以免发⽣太⼤时钟误差的积累,从⽽产⽣接收错误。
第二章作业一、填空题1,由电感L电容C谐振频率为ω0并联电阻RO所构成的并联谐振回路的特性阻抗可表示为,品质因数可表示为。
30、矩形系数k0.1表示选频回路幅频特性中与的比值为0.1。
2,将几个电子器件的输出功率叠加起来以获得足够大的输出功率,这种技术称之为技术。
3,噪声系数是指线性四端网络与的比值。
4,信噪比是在指定频带内,同一端口和的比值。
5,LC回路并联谐振时,回路_ _最大,且为纯__ _。
二、选择题1,LC并联谐振回路在谐振时,相移为;当信号频率ω<谐振频率ω0时,回路呈感性,相移为;当ω>ω时,回路呈容性,相移为。
A、正值B、负值C、零D、不一定2,并联谐振回路的Q值越大,幅频特性曲线越、通频带越,相频特性越。
A、陡峭B、平缓C、宽D、窄3,并联谐振回路处于谐振状态时,回路导纳,阻抗,回路呈现为,信号频率低于谐振频率时回路呈。
A、感性B、容性C、最大D、最小E、纯电阻4,矩形系数越,表示选频回路选择性越好。
A,大 B,小 C,越接近于1 D,不稳定5,串联谐振回路谐振时,回路阻抗为____,回路电流为_____,与外加电压_____,当外加电压的频率大于谐振频率时,回路呈____。
A、反相B、同相C、感性D、容性E、最小值F、最大值G、纯电阻性6,图示传输线变压器的作用分别是:(a)(b)(c)(d)A 反相器B ,平衡转换 C,阻抗变换 D,功率合成三、计算题1,已知并联谐振回路的L=1uH ,C=20P F ,Q=100,求该并联回路的谐振频率f O 、谐振电阻Rp 及通频带BW 0.7 。
2,图示电路中L=0.8μH ,C1=C2=20pF ,CS=5pF ,Rs=10k Ω,CL=20pf ,RL=5 kΩ,QO=100,求回路在有载情况下的谐振频率fo 、电阻Rp (不计Rs 和 RL ,)、QL 值和通频带B 。
3,设一放大器以简单并联振荡回路为负载, 信号中心频率f s=10MHz, 回路电容C =50 pF,(1) 试计算所需的线圈电感值。
第二章作业答案(一)1、某地区在编制材料预算价格时,确定每年需某型号钢材50000t,调入情况如下:用加权平均法计算其原价计算解:(1050×25000+1450×15000+1600×10000)/50000=1280元/t2、某装饰公司采购1000m2的花岗石至施工现场,已知该材料出厂价为1000元/m2,运杂费30元/m2,当地供销部门手续费为1%,采购及保管费率为1%,单位材料里检验试验费为3元/m2,则这批花岗石的材料费用为多少?解:材料预算单价=(材料原价+运杂费+手续费)*(1+采购保管费率)+材料检验试验费=(1000+30+1000*1%)* (1+1%)*1000+3*1000=105.34万元3、某工地水泥从两个地方采购,其采购量及有关费用如下所示,则该工地的水泥基价为多少元/吨?(采购及保管费率为3%)采购处采购量原价运杂费运输损耗费来源一300吨240元/吨20元/吨0.5%来源二200吨250元/吨15元/吨0.4% 解:材料原价=(240*300+250*200)/500=244元/吨材料运杂费=(20*300+15*200)/500=18元/吨运输损耗费={(240+20) *0.5%*300+(250+15) *200*0.4%}/(300+200)=1.204元/吨基价= (材料原价+运杂费+运输损耗费)*(1+采购保管费率)=(244+18+1.204) * (1+3%)=271.1元/吨第二章作业(2)1、某施工机械耐用总台班为800台班,大修周期数为4,每次大修理费用为1200元,则该机械的台班大修理费为()元。
解:台班大修理费=(一次大修理费*寿命期内大修理次数)/耐用总台班其中耐用总台班=大修间隔台班*大修周期大修周期=耐用总台班/大修间隔台班又:大修周期=寿命期大修理次数+1所以,寿命期大修理次数=大修周期-1台班大修理费=(一次大修理费*寿命期内大修理次数)/耐用总台班=[1200*(4-1)]/800=4.5元2、某施工机械预计使用年限内的耐用总台班是2400台班,机械预算价格是360万元,残值率是5%,时间价值系数是1.25,则该机械的台班折旧费是()元。
第⼆章习题答案(作业)第⼆章习题答案2(1)为什么计算机内部采⽤⼆进制表⽰信息?既然计算机内部所有信息都⽤⼆进制表⽰,为什么还要⽤到⼗六进制和⼋进制数?参考答案:(略)2(7)为什么计算机处理汉字时会涉及到不同的编码(如,输⼊码、内码、字模码)?说明这些编码中哪些是⽤⼆进制编码,哪些不是⽤⼆进制编码,为什么?参考答案:(略)3.实现下列各数的转换。
(1)(25.8125)10= (?)2= (?) 8= (?) 16(2)(101101.011)2 = (?)10= (?) 8= (?) 16= (?) 8421(3)(0101 1001 0110.0011)8421 = (?)10= (?) 2= (?) 16(4)(4E.C)16 = (?)10= (?) 2参考答案:(1)(25.8125)10 = (1 1001.1101)2 = (31.64) 8 = (19.D) 16(2)(101101.011)2 = (45.375)10 = (55.3) 8 = (2D.6) 16 = (0100 0101.0011 0111 0101) 8421(3)(0101 1001 0110.0011)8421 = (596.3)10 = (1001010100.01001100110011…) 2 = (254.4CCC…) 16 (4)(4E.C)16 = (78.75)10 = (0100 1110.11) 24.假定机器数为8位(1位符号,7位数值),写出下列各⼆进制数的原码和补码表⽰。
+0.1001,–0.1001,+1.0,–1.0,+0.010100,–0.010100,+0,–0参考答案:(后⾯添0)原码补码+0.1001:0.1001000 0.1001000–0.1001: 1.1001000 1.0111000+1.0:溢出溢出–1.0:溢出 1.0000000+0.010100:0.0101000 0.0101000–0.010100: 1.0101000 1.1011000+0:0.0000000 0.0000000–0: 1.0000000 0.00000005.假定机器数为8位(1位符号,7位数值),写出下列各⼆进制数的补码和移码表⽰。
第二章作业16、在一台机器半球辐射面上的5个测点,测得声压级如下表所示。
计算第5测点的指向性指数和指向性因数。
10、在半自由声场中,一点声源辐射半球面波。
气温20℃、相对湿度20%。
在距声源10m处,测得1000Hz的声压级为100dB,问100m处该频率的声压级为多少分贝?12、某点附近有2台机器,当机器都未工作时,该点的声压级为50dB;若同时工作时,该点的声压级为60 dB;若其中1台工作时,则该点的声压级为55dB,试求另一台机器单独工作时,该点的声压级为多少?13、在某测点处噪声的倍频带声压级列于下表,计算该噪声的总声压级。
14、某声源在指定测点处,测得治理前、后的声压级如表中所示。
计算治理前后的总响度和响度下降的百分率。
15、在空间某处测得环境噪声的倍频程声压级如下表,求其线性声压级和A计权声压级。
(1)若已知一声源的各倍频程声压级,计算声源的总声压级时,公式为:Lpt=10lg (10^0.1L1+10^0.1L2+……10^0.1Ln(2)(3));(2)若已知一声源的各倍频程声压级,计算声源的A声级时,应注意对各倍频程声压级进行修正后,再应用上述公式进行计算。
中心频率(Hz) 63 125 250 500 1000 2000 4000修正值 -26.2 -16.1 -8.6 -3.2 0.0 +1.2 +1.0 线性声压级和A计权声压级:声级计通过计权特性测得的分贝数,称为计权声压级或声级;而不通过计权特性测得的分贝数称为线性声压级或声压级。
19、甲在82dB(A)的噪声下工作8h;乙在81dB(A)的噪声下工作2h,在84dB(A)的噪声下工作4h,在86dB(A)的噪声下工作2h,问谁受到的危害大?21、对某区域进行24h监测,测得A声级如下表所示,计算该区域的昼夜等效声级。
1、案例资料
已知:某企业只生产一种产品,2006年下半年的产销量和相关总成本的历史资料如下:
8月份该企业对其全部成本按性态进行了分类,结果是:当月的固定成本为60,000元,变动成本为10,000元,其余为混合成本。
假定产销量在相关范围内变动。
根据已知资料整理列表如下
要求:用高低点法和回归分析法进行成本性态分析
2、某企业铸造车间的燃料用于铸造熔炉,分别在点炉和熔化铁水两个程序中使用。
最佳操作方法是:每次点炉要用木柴0.08吨,焦炭1.2吨;熔化1吨铁水使用焦炭0.12吨,每个工作日点炉一次,全月工作24天,木柴250元/吨,焦炭400元/吨。
确定该车间每月燃料总成本方程。
3、设某企业只生产一种产品,第一、第二、第三各年的生产量(基于其正常生产能力)都是8000件,而销售量分别为8000件、7000件和9000件。
单位产品的售价为12元。
生产成本:单位变动成本(包括直接材料、直接人工和变动制造费用)5元。
固定制造费用基于正常生产能力8000件,共计24000元,每件产品应分摊3元(24000/8000)。
销售和行政管理费假定全部都是固定成本,每年发生额均为25000元。
要求:根据上述资料,不考虑销售税金,分别采用变动成本法和完全成本法计算各年税前利润。