稳态第五章2
- 格式:pdf
- 大小:499.25 KB
- 文档页数:39

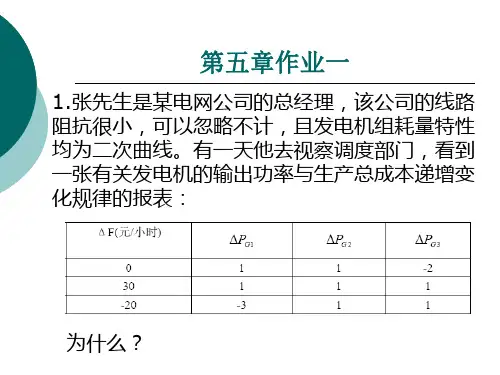
1、两台发电机容量均为100MW ,耗量特性分别为:211110.20.002G G F P P =++ (t/h )222230.10.002G G F P P =++ (t/h )两台发电机同时供一个负荷L P ,试求:1)当系统负荷L P =65MW 时,120G P MW =,245G P MW =分配负荷是不是最优方案?2)当L P =160MW 时,两发电机间的最优分配方案是多少?解:1)⎪⎪⎩⎪⎪⎨⎧+==+==22221111004.01.0004.02.0G G G G P dP dF P dP dF λλ(1分), 当120G P MW =,245G P MW =代入上式令212128.045*004.01.028.020*004.02.0λλλλ=⇒⎭⎬⎫=+==+=,所以是最优分配。
2)当L P =160MW 时5.92,5.67160004.01.0*004.02.02121211==⇒⎭⎬⎫=++=+=G G G G G G P P P P P P λ2、三个火电厂并列运行,各发电厂的耗量特性F (t/h )及功率约束条件如下:(10分)21114.00.300.00070G G F P P =++ 100MW 1G P≤≤200MW 1T 22223.50.320.00040G G F P P =++ 120MW 2G P≤≤250MW 23333.50.300.00045G G F P P =++ 150MW 3G P ≤≤300MW 当总负荷为700MW 和400MW 时,试分别确定发电厂间功率的经济分配(不计网损影响) 解:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+==+==+==3333222211110009.03.0008.032.00014.03.0G G G G G G P dP dF P dP dF P dP dF λλλ 令321λλλ==⎩⎨⎧+=++=+32210009.03.00008.032.00008.032.00014.03.0G G G G P P P P MW P MW P MW P P P P G G G G G G 274,250,176700321321===⇒=++3、某系统的综合负荷单位调节功率为Hz MW /500,系统负荷增大1000MW 时,调频厂经二次调频增发的500MW ,系统频率变化为0.2Hz ,求系统的发电机的单位调节功率? 答:4、 A 、B 两系统中,A 、B 两系统的容量分别是3000MW 、2000MW ,25*=G A K ,6.1*=LA K ,20*=G B K ,4.1*=LB K ,MW PLA 200=∆时,求 (1) 系统A 、B 的机组都参加一次调频后系统频率的变化值;(2) 若A 、B 两系统的机组都参加一次调频,且B 系统部分机组参加二次调频增发50MW 时,求统频率偏移以及联络线上流动的功率。





第五章电力系统的有功功率和频率调整第二节电力系统中的有功功率的最优分配(发电计划,解决三次调整)三、最优分配负荷时的目标函数和约束条件●一个时间断面下的经济功率分配●耗量特性:发电设备输入与输出的关系。
–比耗量:耗量特性曲线上某一点纵坐标和横坐标的比值,即单位时间内输入能量与输出功率之比称比耗量μ。
显然,比耗量实际是原点和耗量特性曲线上某一点连线的斜率,μ=F/P 或μ=W/P。
–发电效率:当耗量特性纵横坐标单位相同时,比耗量的倒数就是发电设备的效率η。
–耗量微增率:耗量特性曲线上某一点切线的斜率称耗量微增率λ。
耗量微增率是单位时间内输入能量微增量与输出功率微增量的比值,即dP dF P F //=∆∆=λ或dP dW P W //=∆∆=λ–对于一台机组,比耗量曲线和耗量微增率曲线的交点是单台发电机效率最高的点。
–若耗量特性曲线为二次曲线F=aP2+bP+C –则μ=aP+b+c/P,λ=2aP+b。
–若耗量特性曲线为F=aP2+bP–则μ=aP+b,λ=2aP+b。
–若耗量特性曲线为一次曲线F =bP–则μ=λ=b。
目标函数和约束条件–问题的提出:负荷最优分配的目的在于:确定电网中每台机组的有功功率输出,在满足负荷需求、系统安全的同时,使单位时间内的能源消耗最少。
–优化问题的通用模型d u x g 0d u x f d u x C ≤=),,(),,(..),,(t s Min式中C 为目标函数,f 为等式约束,g 为不等式约束–最优分配负荷时的目标函数和约束条件•目标函数:∑=∑=+++=ni Gi i Gn n G G P F P F P F P F F 12211)()()()( –其中:)(Gi i P F 表示发电机i 的耗量曲线•等式约束(不计网损)11=∆--∑==∑∑P P P n i Li n i Gi•不等式约束(发电有功、无功,节点电压幅值)GimaxGi Gimin P P P ≤≤GimaxGi Gimin Q Q Q ≤≤imaxi imin U U U ≤≤•系统中发电设备消耗的能源可能受限制。

第五章作业5-1 何谓一次调频?一次调频能使频率保持不变吗?是否所有机组都能进行一次调频?一次调频是如何实现的?5-2 何谓二次调频?二次调频能使频率保持不变吗?是否所有机组都担负二次调频任务?二次调频是如何实现的?5-3 系统总负荷5000 MW ,正常运行频率f N =50,若因为事故失去250 MW 发电出力,最后系统频率稳定在48赫兹,求系统负荷的频率调节效应系数K L 。
5-4某地区系统,发电厂容量为3000kW ,调差系数为2.5%;负荷的频率调节效应系数是1.5。
当负荷为1500kW 时,系统频率为50Hz 。
现因负荷变化,频率下降到49.9Hz 。
试计算系统负荷的变化量为多少?是增加还是减少?系统负荷实际消耗的功率是多少?5-5 有两台100MW 的机组并列运行,调速器下降特性(机组由空载到满载转速变化百分数)分别为4%和5%,负荷为150MW 。
(a )负荷在两机组间如何分配?(b )要使两机组平均分担负荷,应如何调整?5-6系统f N =50,总装机容量2000MW ,P LN =1600MW ,调差系数σ% = 5,K L =50MW/H Z ,在额定频率下运行时增加负荷430 MW ,求下列情况下系统的频率变化。
(1)所有发电机组仅参加一次调频,(2)所有发电机组都参加二次调频。
5-7系统中发电机组的容量和它们的调差系数分别为:水轮机组:100MW/台 ⨯ 5台=500, σ% = 2.5; 汽轮机组:50MW/台 ⨯20台=1000,σ% = 3.5; 75MW/台 ⨯ 5台=375, σ% = 2.75; 100MW/台 ⨯ 6台=600,σ% = 3.5; 其它容量汽轮机组等效为1000MW ,σ% = 4。
系统f N =50,P LN =3500MW******,K L * = 1.5 。
若(1)全部机组都参加一次调频,(2) 全部机组都不参加一次调频(3)仅水轮机组参加一次调频,当系统负荷增加到3300 MW 时,系统频率为多少?(4)要求频率无差调节,发电机的二次调频功率为多少?(5)要求频率不低于49.8,发电机的二次调频功率为多少?5-8 有两系统A 和B ,它们的情况如下:A 系统:容量1500MW ,25*=GA K ,6.1*=LA KB 系统:容量2000MW ,*35GB K =,* 1.2LB K =(标么值基准为各系统容量及50Hz )现在,A 系统负荷增加150MW ,试计算下列两种情况下频率的变化量,以及联络线上功率的变化量,并说明频率是增加还是减少,以及联络线功率的流向。
(新教材)部编人教版高中生物选择性必修一《稳态与调节》第五章第二节《其他植物激素》优质说课稿今天我说课的内容是人教版高中生物选择性必修一《稳态与调节》的第5章第二节《其他植物激素》。
植物与动物在生命活动的调节方式上具有明显的区别。
在植物生命活动的调节中,最重要的是植物生命活动的调节,此外,环境因素也参与调节。
植物生命活动调节的原理在农业、园艺等生产活动中有着广泛的应用,因此,本章内容具有重要的实践应用价值。
第二节课介绍其他植物激素的种类和作用。
为了能更好地实现本章教学目标,现从教学等方面进行说课。
一、说课程标准。
本节对应于课标上的内容要求是:“1.6 植物生命活动受到多种因素的调节,其中最重要的是植物激素的调节。
1.6.2 举例说明几种主要植物激素的作用,这些激素可通过协同、拮抗等方式共同实现对植物生命活动的调节。
”二、教材分析。
本节以问题探讨引入,引起学生对其他植物激素的关注。
接着教材先叙述了其他植物激素的种类的发现,然后以图文形式讲解其他植物激素的合成部位和主要作用。
最后教材以思考讨论、图文结合形式阐述植物激素间的相互作用。
教材图文并茂,讲解详细。
三、说教学目标和核心素养。
(一)教学目标1.举例说出赤霉素、细胞分裂素、乙烯、脱落酸的作用。
2.举例说明植物激素之间存在复杂的相互作用。
(二)核心素养1.生命观念:植物激素、环境因素,对于植物生命活动的调节来说,都是作为信息而起作用的。
植物激素实质上就是信息分子。
因此,本章内容的学习,可以进一步建立生命的信息观。
植物生命活动的调节,无论是植物激素之间,还是植物激素、环境因素,以及基因表达之间,都存在着复杂的相互联系;植物生命活动的有序进行,依赖复杂的调控网络进行调节。
由此,可以进一步领会生命系统的复杂性。
2.科学思维:从问题探讨到思考讨论,从文字到图片,教材无不渗透出科学思维的训练和培养。
3.科学探究:从问题探讨到思考讨论,从文字到图片,教材无不渗透出科学探究精神的培养。
第五章 电力系统的有功功率和频率调整第二节 电力系统中的有功功率的最优分配(发电计划,解决三次调整)三、最优分配负荷时的目标函数和约束条件z 一个时间断面下的经济功率分配z 耗量特性:发电设备输入与输出的关系。
– 比耗量:耗量特性曲线上某一点纵坐标和横坐标的比值,即单位时间内输入能量与输出功率之比称比耗量μ 。
显然,比耗量实际是原点和耗量特性曲线上某一点连线的斜率, μ =F/P 或μ =W/P。
– 发电效率:当耗量特性纵横坐标单位相同时,比耗量的倒数就是发电设备的效率η 。
– 耗量微增率:耗量特性曲线上某一点切线的斜率称耗量微增率λ 。
耗量微增率是单位时间内输入能量微增量与输出功率微增量的比值,即dP dF P F //=ΔΔ=λ或dP dW P W //=ΔΔ=λ – 对于一台机组,比耗量曲线和耗量微增率曲线的交点是单台发电机效率最高的点。
–若耗量特性曲线为二次曲线F = aP2 + bP + C –则μ=aP+b+c/P, λ=2aP+b。
–若耗量特性曲线为F = aP2 + bP–则μ=aP+b, λ=2aP+b。
–若耗量特性曲线为一次曲线F = bP –则μ=λ=b。
z 目标函数和约束条件 – 问题的提出:负荷最优分配的目的在于:确定电网中每台机组的有功功率输出,在满足负荷需求、系统安全的同时,使单位时间内的能源消耗最少。
– 优化问题的通用模型d u x g 0d u x f d u x C ≤=),,(),,(..),,(t s Min式中C 为目标函数,f 为等式约束,g 为不等式约束– 最优分配负荷时的目标函数和约束条件• 目标函数:∑=Σ=+++=ni Gi i Gn n G G P F P F P F P F F 12211)()()()(" – 其中:表示发电机i 的耗量曲线)(Gi i P F • 等式约束(不计网损)011=Δ−−Σ==∑∑P P P ni Li n i Gi • 不等式约束(发电有功、无功,节点电压幅值)Gimax Gi GiminP P P ≤≤ Gimax Gi GiminQ Q Q ≤≤imax i imin U U U ≤≤• 系统中发电设备消耗的能源可能受限制。
例如,水电厂一昼夜间消耗的水量受约束于水库调度。
出现这种情况时,目标函数就不应再是单位时间内消耗的能源,而应是一段时间内消耗的能源,即应为 ∑∫==Σ=m i i Gi i dt P F F 10)(τ• 而等约束条件除式(5—2)外,还应增加∫=τ0)(定值dt P W Gi j • 这里的F i ,可理解为单位时间内火力发电设备的燃料消耗;为单位时间内水力发电设备的水量消耗;τ为时间段长,例如24h。
而这里设i=1,2,…,m 为火力发电设备,j =(m 十1),(m 十2),…,n 为水力发电设备。
W j 四、最优分配负荷的等耗量微增率准则z 公式推导:¾ 问题的简化• 略去不等式约束• 仅有两台机组¾ 推导:• 目标函数)()(),(221121G G G G P F P F P P C C +==• 约束条件0),(2121=−+=LD G G G G P P P P P f• 拉格朗日函数)()()(),(),(2122112121*LD G G G G G G G G P P P P F P F P P f P P C C −+−+=−=λλ• 原问题变成求拉格朗日函数的最小值,将有约束极值问题转化为无约束极值问题,λ称为拉格朗日乘数。
当然,天下没有白吃的午餐,去掉了一个等式约束,但增加了一个变量λ • 极值条件: ;0;0;0*2*1*=∂∂=∂∂=∂∂λC P C P C G G • 展开: ⎪⎪⎪⎭⎪⎪⎪⎬⎫==∂∂−∂∂=∂∂−∂∂0),(0),(),(0),(),(21221221121121G G G G G G G G G G G G G G P P f P P P f P P P C P P P f P P P C λλ• 解出:⎪⎪⎪⎭⎪⎪⎪⎬⎫==−=−0),(0)(0)(21222111G G G G G G P P f dP P dF dP P dF λλ • 由于 111)(G G dP P dF ,222)(G G dP P dF 分别为发电设备1、2各自承担• 有功功率负荷PG1、PG2时的耗量微增率λ1、 λ2,可以得到: λ1= λ2= λ,这就是等耗量微增率准则,它表示为使总耗量最小,应该按相等的耗量微增率在发电设备或发电厂之间分配负荷。
¾ 物理意义:•对于这个简单问题,可以用作图法求解。
设上图中线段OO’的长度等于负荷功率PLD。
在线段的上、下两方分别以O和O’为原点做出机组1和2的燃料消耗特性曲线1和2,前者的横坐标PG1自左向右,后者的横坐标PG2自右向左。
•显然,在横坐标上任取一点A,都有OA十AO’=OO’,即 PG1 +PG1= PLD 。
因此,横坐标上的每一点都表示一种可行的(满足约束条件的)功率分配方案。
•如过A点作垂线分别交于两机组耗量特性曲线的B1和B2点,则B1B2=B1A+AB1=F1(PG1)+F2(PG2)=C就代表了总的燃料消耗量。
•由此可见,只要在OO’上找到一点,通过它所作垂线与两耗量特性曲线的交点距离为最短,则该点所对应的负荷分配方案就是最优的.•图中的点A’ 就是这样的点,通过A’点所作垂线与两特性曲线的交点为B1’和B2’。
在耗量特性曲线具有凸性的情况下,曲线1在B1’点的切线与曲线2在B2’点的切线相互平行。
耗量曲线在某点的斜率即是该点的耗量微增率。
由此可得结论:负荷在两台机组间分配时,如它们的燃料消耗微增率相等.¾ 公式推广(多发电设备或发电厂):),,,(),,,(2121*Gn G G Gn G G P P P f P P P C C ""λ−=• 推出 ⎪⎪⎭⎪⎪⎬⎫=−==−∑==0),,2,1(0)(1LD n i i Gi GiGi i P Pn i dP P dF "λ • 结论: λ1= λ2= …= λn =λ¾ 对于不等式约束,可以使用kuhn-Tucker 条件解决。
¾ 关于电压和无功的约束,与有功功率负荷分配没有直接关系,省略。
¾ 对于发电设备有功输出功率的约束,当发生越限时。
将发电设备有功输出功率固定在边界上。
z 计算步骤:五、等耗量微增率准则的推广运用z 公式推导:¾ 问题的简化• 略去不等式约束• 仅有一台火力发电单元和一台水力发电单元¾ 推导:• 目标函数∫=Στ011)]([dt t P F F T • 约束条件2022)]([K dt t P W H =∫τ 021=−+LD H T P P P• K2为水力发电设备2在0到τ时间内 规定消耗的水量。
将0到τ时间分成t 个时段: k t k k k T k t P F F Δ=∑==⋅⋅Σ111)(2122)(K t P Wk t k k k H k =Δ∑==⋅⋅ 021=−+⋅⋅⋅k LD k H k T P P P• 建立拉格朗日函数])([][)(21222121111*K t P W t P P P t P F C k t k k k H k k tk k LD k H k T k k t k k k T k −Δ+Δ−+−Δ=∑∑∑==⋅⋅==⋅⋅==⋅⋅γλ• 其中λ1、λ2……λt 和γ2 都是拉格朗日乘数,其中γ2 是由于引入水电厂的约束条件而新增加的。
• 极值条件;0;0;0;02**2*1*=∂∂=∂∂=∂∂=∂∂⋅⋅γλC C P C P C k k H k T• 展开 ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=−Δ==−+==−==−∑==⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅0)(),,2,1(0),,2,1(0)(),,2,1(0)(2122212222111K t P W t k P P P t k dP P dW t k dP P dF t k k k k H k LD k H k T k k H k H k k kT k T k """λγλ • 一共(3t+1)个独立方程,变量也是(3t+1)个,可以求解。
• 第一、二式合并,可得 ),,2,1()()(2222111t k dP P dW dP P dF k k H k H k kT k T k "===⋅⋅⋅⋅⋅⋅λγ• 略去下标k,得到 λγ==2222111)()(H H T T dP P dW dP P dF• 式中,111)(T T dP P dF 为火力发电厂的燃料耗量微增率 • 111)(T T dP P dF 为水力发电厂的水耗量微增率 • 上式可改为:λλγλ==221H T• 由上式可见,只要将水力发电的水耗量微增率乘以某一个待定的拉格朗日乘数γ2 ,就可将指导火力发电设备(厂)之间负荷最优分配的等耗量微增率准则推广运用于火力发电设备(厂)与水力发电设备(厂)之间负荷的最优分配。
为此,需确定拉格朗日乘数γ2 。
这乘数为 )()()()(22112221112H T H H T T P dW P dF dP P dW dP P dF ==γ • 式中分子、分母上的dPT1、dPH2之所以可相约,是由于问题仅涉及增减同样大小有功功率时火力或水力发电设备燃料或水耗量增减的多少。
由式可见,如F1的单位为t/h,W2的单位为,则γ2的单位为 h m /33/m t•因此,这个拉格朗日乘数γ2实际上可看作是一个换算系数.•既然γ2可看作换算系数,水力发电设备(厂)在一定时间内可消耗的水量越多,单位重量燃料可折换的水量就愈大, γ2从而γ2λH2也就愈小,按等耗量微增率准则水力发电设备(厂)应分配的负荷也就愈大;反之,水力发电设备(厂)应分配的负荷愈小。
六、网络损耗的修正:网络上不同地点上的发电机在发电时,对网损的影响不同,也就是说这些发电机即使有相同的发电功,它们对负荷的贡献也是不一样的。
例如:率假设G1、G2煤耗曲线相同,P1>P2,如果不考虑网损修正,果考虑网损,则(P1+P2)/2<G1<P1、P2<G2<(P1+P2)/2其实,在电力市场中电力交易软件也要对各机组的报价进行网损折算,原理一样。
则G1=G2=(P1+P2)/2最好,但是如时最为节省。