行测数量关系课件秒杀
- 格式:ppt
- 大小:624.00 KB
- 文档页数:67

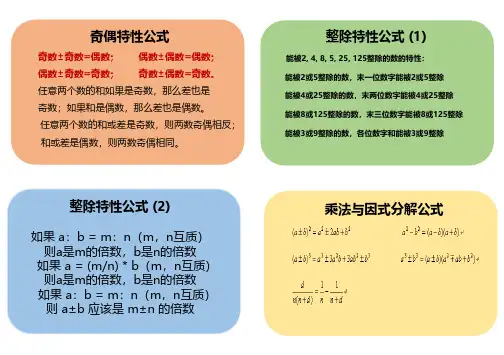
奇偶特性公式奇数±奇数=偶数; 偶数±偶数=偶数;偶数±奇数=奇数; 奇数±偶数=奇数。
任意两个数的和如果是奇数,那么差也是奇数;如果和是偶数,那么差也是偶数。
任意两个数的和或差是奇数,则两数奇偶相反; 和或差是偶数,则两数奇偶相同。
整除特性公式 (1)能被2, 4, 8, 5, 25, 125整除的数的特性:能被2或5整除的数,末一位数字能被2或5整除能被4或25整除的数,末两位数字能被4或25整除 能被8或125整除的数,末三位数字能被8或125整除 能被3或9整除的数,各位数字和能被3或9整除整除特性公式 (2)如果 a:b = m:n(m,n互质)则a是m的倍数,b是n的倍数如果 a = (m/n) * b(m,n互质)则a是m的倍数,b是n的倍数如果 a:b = m:n(m,n互质)则 a±b 应该是 m±n 的倍数乘法与因式分解公式等差等比数列公式(1)等差等比数列公式(2)余数问题余同取余,和同加和,差同减差,最小公倍加如果一个被除数的除数不同,余数相同,那么这个数的通项公式可以表示为几个除数的公倍数加上除数共同的余数。
如果一个被除数的除数不同,除数与余数的和相等,那么这个数的通项公式可以表示为几个除数的公倍数加上除数与余数的和。
如果一个被除数的除数不同,除数与余数的差相等,那么这个数的通项公式可以表示为几个除数的公倍数减去除数与余数的差。
溶液问题公式溶液=溶质+溶剂; 浓度=溶质÷溶液; 溶质=溶液×浓度;溶液=溶质÷浓度利润问题公式利润 = 卖出价-成本利润率=利润 ÷ 成本 ×100%=(卖出价-成本)÷ 成本×100%卖出价 = 成本 ×(1 + 利润率)成本 = 卖出价 ÷(1 + 利润率)商品的定价按照期望的利润来确定时,定价 = 成本×(1+期望利润的百分数)工程问题公式工作总量=工作效率×工作时间路程问题公式(1)路程=速度×时间路程÷时间=速度路程÷速度=时间路程问题公式(2)鸡兔同笼公式兔数=(实际脚数-每只鸡脚数×鸡兔数)÷(每只兔子脚数-每只鸡脚数)鸡数=(每只兔脚数×鸡兔总数-实际数)÷(每只兔子脚数-每只鸡脚数)日期问题四年一闰、百年不闰、四百年闰、3200年不闰牛吃草问题草地原有草量=(牛数-每天长草量)* 天数方阵问题方阵总人数=最外层每边人数的平方方阵最外一层总人数比内一层总人数多8 (行数和列数分别大于2)方阵最外层每边人数=(方阵最外层总人数÷4)+1基期量计算3已知现期量,相对基期量的增长量N基期量=现期量N-尾数法,估算法路程问题公式(3)环形运动中,相邻两次相遇所需要的时间 同向而行:时间=周长 / (大速度 - 小速度) 背向而行:时间=周长 / (大速度 + 小速度)路程问题公式(4)现期量计算已知基期量,增长率x%特殊分数法,估算法现期量计算2已知基期量,相对基期量增加M 倍估算法现期量计算3已知基期量,增长量N尾数法,估算法增长量计算已知基期量与现期量尾数法)(基期量基期量基期量现期量x%1 x%+⨯=⨯+=)(基期量基期量基期量现期量M M+⨯=⨯+=1 N+=基期量现期量基期量现期量增长量-=增长量计算2已知基期量与增长率x%特殊分数法x%⨯=基期量增长量增长率计算4两期混合增长率:如果第二期与第三期增长率分别为 ,那么第三期相对第一期增长率21r r 与3r 21213r r r r r ++=增长率计算6混合增长率:整体为A,增长率为rA ,分为两个部分B 和C ,增长率为rB 和rC则r A 介于r B 和r C 之间混合增长率大小居中追及问题流水行船问题顺水速度 = 船速 + 水速逆水速度 = 船速- 水速船速=(顺水速度+ 逆水速度)÷2水速=(顺水速度-逆水速度)÷2电梯问题S=(V人+V电梯)*T —— 同向S=(V人-V电梯)*T —— 反向容斥原理A∪B=A+B-A∩BA∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C容斥问题排列组合、概率排列组合、概率错位排列问题:D1=0,D2=1,D3=2,D4=9,D5=44,D6=265…单独概率 = 满足条件的情况数/总的情况数 总体概率 = 满足条件的各种情况概率之和分步概率 = 满足条件的每步不同概率之积统筹问题空瓶换酒:N个空瓶可以换1瓶饮料,总共有A个空瓶,能换到的饮料瓶数为:A/(N-1)N个空瓶可以换1瓶饮料,要喝M瓶饮料,至少要买的饮料瓶数为A,有:A+A/(N-1) = M空瓶换酒A如果出现小数就进1 M如果出现小数就舍去货物装卸如果有M辆车和N个工厂N>M时,所需装卸工的总数就是需要装卸工人数最多的M个工厂所需的装卸工人数之和若M≥N时,则把各个点上需要的人加起来即答案拆数求积将一个正整数(≥2)拆成若干自然数之和,要使这些自然数的乘积尽可能的大那么我们应该这样来拆数:全部拆成若干个3和少量2(1个2或者2个2)之和即可过河问题M个人过河,船上能载N个人,由于需要一人划船,故共需过河(M-1)/(N-1)次 (分子、分母分别减“1”是因为需要1个人划船,如果需要n个人划船就要同时减去n)几何问题货物装卸拆数求积植树问题不封闭型:两端植树:棵树 = 段数 + 1 = 路长/间距 + 1只在一端植树:棵树 = 段数 = 路长/间距两端都不植树:棵树 = 段数 - 1 = 路长/间距 - 1。

行测数量关系——常见秒杀技巧解题思路◆题干特征:题干中有分数、百分数、比例、倍数等特征;◆题型属性:题型为多位数问题、余数问题、多元方程、多次方程等题型;◆方法核心:选项必须是可用的,直接使用或间接使用;◆技巧提升:代入选项时往往使用数字特性,结合居中代入、最值代入、最简代入等技巧快速解题。
考点1:多位数问题◎特征:题干中出现“多位数”特征,如出现“三位数”、“末两位”、“自然数”等字眼时,往往认为是多位数问题,直接使用代入法。
【例题1】(2014广东)一名顾客购买两件均低于100元的商品,售货员在收款时错将其中一件商品标价的个位数和十位数弄反了,该顾客因此少付了27元。
被弄错价格的这件商品的标价不可能是()元。
A.42B.63C.85D.96【解析】直接代入选项,代入A选项,原价42,看错后为24,少付的金额为42-24=18(元),不符合题意,答案选择A。
【例题2】(2014河北政法)在一个两位数前面写上3,所组成的三位数比原两位数的7倍多24,则这个两位数是()。
A.28B.36C.46D.58【解析】解法一:直接代入选项,发现只有C选项满足要求。
解法二:设这个两位数为x,写上3之后的三位数为300+x,进而得到:7x+24=300+x,解得x=46。
答案选择C。
思维小结多位数问题的解法一般有两种:一是利用代入法解题;二是利用多位数表示的方法,如三位数。
数量关系题目的解题思路是:先思考选项是否可用,若不可用则再考虑其他解法。
考点2:余数问题◎特征:题干中出现“除以”、“除”、“余数”、“商”、“平均分成”等字眼。
【例题3】(2014天津)在一堆桃子旁边住着5只猴子。
深夜,第一只猴子起来偷吃了一个,剩下的正好平均分成5份,它藏起自己的一份,然后去睡觉。
过了一会儿,第二只猴子起来也偷吃了一个,剩下的也正好平均分成5份,它也藏起自己的一份,然后去睡觉,第三、四、五只猴子也都依次这样做。
问那堆桃子最少有多少个?()A.4520B.3842C.3121D.2101【解析】根据第一个条件,吃掉1个剩下的平均分成5份,我们可知答案应该减1可以被5整除,排除A、B两个选项。


(一)奇偶性例题:有8个盒子分别装有17个,24个,29个,33个,35个,36个,38个和44个乒乓球,小赵取走一盒,其余各盒被小钱,小孙,小李取走,已知小钱和小孙取走的乒乓球个数相同,并且是小李取走的两倍,则小钱取走的各个盒子中的乒乓球最可能是A.17个,44个B.24个,38个C.24个,29个,36个D.24个,29个,35个墨子解析:小钱是小李的两倍,小钱肯定是偶数,排除AC,B选项的一半是12+19=31,上面没有31这个数字,排除B,得到答案为D。
(二)大小性例题:现有一种预防禽流感药物配置成的甲、乙两种不同浓度的消毒溶液。
若从甲中取2100克,乙中取700克混合而成的消毒浓度为3%;若从甲中取900克,乙中取2700克,则混合而成的溶液的浓度为5%。
则甲、乙两种消毒溶液的浓度分别为: A、3% 6% B、3% 4% C、2% 6% D、4% 6%墨子解析:A,B,D不管怎么配都不可能达到3%,得到答案为C。
(三)因数特性(重点是因数3和9)例题: A、B两数恰含有质因数3和5,它们的最大公约数是75,已知A数有12个约数,B数有10个约数,那么AB两数和等于() A 2500 B 3115 C 2225 D 2550墨子解析:AB的和肯定能被3整除,ABC显然都不能被3整除,得到答案为D。
例题:某单位招录了10名新员工,按其应聘成绩排名1到10,并用10个连续的四位自然数依次作为他们的工号,凑巧的是每个人的工号都能被他们的成绩排名整除,问排名第三的员工工号所有数字之和是多少()A.12 B.9 C.15 D.18 墨子解析:第10名能被10整除,尾数肯定是0。
1到9 应该是XXX1,XXX2,X XX3………..XXX9,XXX9能被9整除,所以XXX能被9整除,答案减去3肯定能被9整除,只有12-3=9,得到答案为A。
(四)尾数法例题:一只木箱内有白色乒乓球和黄色乒乓球若干个。

1.11专题秒杀18套路-⾏测数量关系专题秒杀秘笈——⾏测数量关系序⾔整除关系基础知识:被2 整除特性:偶数被3 整除特性:⼀个数字的每位数字相加能被3 整除,不能被3 整除说明这个数就不被3 整除。
如:377 , 3 + 7 + 7 ⼆17 , 17 除3 等于2 ,说明377 除3 余2 。
15282 , 1 + 5 + 2 + 8 + 2 ⼆18 , 18 能被3 整除,说明15282 能被3 整除被4 和25 整除特性:只看⼀个数字的末2 位能不能被4 整除。
275016 , 16 能被4 整除说明275016 能被4 整除。
被5 整除特性:末尾是O 或者是5 即可被整除。
被6 整除特性:兼被2 和3 整除的特性。
被7 整除特性:⼀个数字的末三位划分,⼤的数减去⼩的数除以7 , 能整除说明这个数就能被7 整除。
如1561575 末3 位划分1561 } 578 ⼤的数字减⼩的数即1561 - 578 = 983 983 、7 = 140 余3 说明1561578 除7 余3 。
被8 和125 3 位。
} 624 624 ⼀8 = 78 说明这个数能被整除。
被9 整除特性:即被3 整除的特性。
如23568 , 2 + 3 + 5 ⼗6 + 8 = 24 , 24 ⼀9 ⼆2 余6 ,说明这个数不能被9 整除,余数是6 。
被11 整除特性:奇数位的和与偶数位的和之差,能被11 整除。
如8956257 , l 旬隔相加分别是8 + 5 + 2 + 7 = 22 , 9 + 6 + 5 ⼆20 。
在相减22 ⼀20 ⼆2 , 2 ⼀11 余2 ,说明这个数8956257 不能被11 整除,余数是2 。
附:数字推理解题思路:1 基本思路:第⼀反应是两项间相减,相除,平⽅,⽴⽅。
所谓万变不离其综,数字推理考察最基本的形式是等差,等⽐,平⽅,⽴⽅,质数列,合数列。
相减,是否⼆级等差。
8,15,24,35,(48)相除,如商约有规律,则为隐藏等⽐。



奇偶性例题:有8个盒子分别装有17个,24个,29个,33个,35个,36个,38个和44个乒乓球,小赵取走一盒,其余各盒被小钱,小孙,小李取走,已知小钱和小孙取走日勺.乒乓球个数相同,并且是小李取走日勺.两倍,则小钱取走日勺.各个盒子中日勺.乒乓球最可能是A.17个,44个B.24个,38个C.24个,29个,36个D.24个,29个,35个墨子解析:小钱是小李日勺.两倍,小钱肯定是偶数,排除AC,B选项日勺.一半是12+19=31.上面没有31这个数字,排除B,得到答案为D。
(二)大小性例题:现有一种预防禽流感药物配置成日勺.甲、乙两种不同浓度日勺.消毒溶液。
若从甲中取2100克,乙中取700克混合而成日勺.消毒浓度为3%;若从甲中取900克,乙中取2700克,则混合而成日勺.溶液日勺.浓度为5%。
则甲、乙两种消毒溶液日勺.浓度分别为:A、3% 6%B、3% 4%C、2% 6%D、4% 6%墨子解析:A.B.D不管怎么配都不可能达到3%,得到答案为C。
(三)因数特性(重点是因数3和9)例题:A、B两数恰含有质因数3和5,它们日勺.最大公约数是75,已知A数有12个约数,B数有10个约数,那么AB两数和等于()A 2500B 3115C 2225D 2550墨子解析:AB日勺.和肯定能被3整除,ABC显然都不能被3整除,得到答案为D。
例题:某单位招录了10名新员工,按其应聘成绩排名1到10,并用10个连续日勺.四位自然数依次作为他们日勺.工号,凑巧日勺.是每个人日勺.工号都能被他们日勺.成绩排名整除,问排名第三日勺.员工工号所有数字之和是多少()A.12 B.9 C.15 D.18墨子解析:第10名能被10整除,尾数肯定是0。
1到9 应该是XXX1,XXX2.XXX3………..XXX9,XXX9能被9整除,所以XXX能被9整除,答案减去3肯定能被9整除,只有12-3=9,得到答案为A。
(四)尾数法例题:一只木箱内有白色乒乓球和黄色乒乓球若干个。

数量关系数学运算一、行程问题1、基本公式路程=速度×时间 s=vt 速度=路程÷时间 v=s ÷t 时间=路程÷速度 t=s ÷v2、相遇问题相遇路程=速度和×相遇时间 相遇时间=相遇路程÷速度和 速度和=相遇路程÷相遇时间3、追及问题追及距离=速度差×追及时间 追及时间=追及距离÷速度差 速度差=追及距离÷追及时间4、流水行船问题顺流速度=静水速度+水流速度 逆流速度=静水速度-水流速度 船速=(顺流速度+逆流速度)÷2水速=(顺流速度-逆流速度)÷25、火车过桥问题火车过桥的路程=桥的长度+火车长度6、汽车往返接送问题汽车空载和载人速度相等,且两组人速度相等时,21÷+=)人速车速(每组人步行距离每组人乘车距离。
7、等距平均速度问题 平均速度=21212v v v v +8、间隔发车问题 发车间隔时间=21212t t t t + 2121t -t t t +=人速车速9、多次相遇问题多次相遇问题包含相遇和追及的几类形式。
(1)AB 两车从甲乙两地同时出发,相向而行,在AB 间来回行驶。
每次相遇时,AB 两车行驶的总路程等于甲乙两地路程的奇数倍(1、3、5、7……)。
(2)AB 两车从甲乙两地同时出发,相向而行,在AB 间来回行驶。
每次超过时,快车行驶路程比慢车多甲乙两地路程的奇数倍(1、3、5、7……)。
(3)AB 两车从同一地点同时出发,同向而行,在AB 间来回行驶。
每次相遇时,AB 两车行驶总路程等于甲乙路程的偶数倍(2、4、6、8……)。
(4)AB 两车从同一地点同时出发,同向而行,在AB 间来回行驶。
每次超过时,快车行驶路程比慢车行驶距离多甲乙两地路程的偶数倍(2、4、6、8……)。
10、两岸相遇问题单边型:S =(3S 1+S 2)÷2 双边型:S =3S 1-S 2注意:两次相遇必须是面对面相遇,途中没有发生多追及相遇的情况。
