下载文档原格式
全连接神经⽹络MLP全连接神经⽹络 MLP最近开始进⾏模型压缩相关课题，复习⼀下有关的基础知识。
1. MLP简介上图是⼀个简单的MLP，这是典型的三层神经⽹络的基本构成，Layer L1是输⼊层，Layer L2是隐含层，Layer L3是隐含层。
为了⽅便下⾯的公式描述，引⼊⼀张带公式的图。
i是input层，h是hide层，o是output层。
2. MLP 正向传播正向传播其实就是预测过程，就是由输⼊到输出的过程。
为之前的图⽚赋上初值，上述变量中，存在着如下过程：原始输⼊-> 带权计算-> net_h1-> 激活函数-> out_h1同理，可以计算另⼀个隐层net_h2, out_h2，以及输出层net_o1, net_o2, out_o1, out_o2此时在输出端我们可以得到⼀个预测值，但是在随机初始化权值的情况下，这个值⼀定还有上升的空间，怎么才能使这个值变得更为准确呢？3. MLP 反向传播MLP的反向传播过就是对于神经⽹络的训练过程。
在这⾥，我们训练的是之前各条边上的权值。
3.1 总误差（square error）target为该样本的正确值，output为这⼀轮预测的值。
这⾥存在两个输出，所以，对于所有输出求和，并最终计算E_total推⼴⾄N个输出（分类），则是把N各分类中的输出（⼀般是分类概率）误差分别求出，最终求和。
在这⾥的总误差在下⾯的应⽤时，主要看的是接受到了⼏个误差的影响（如果只接受到⼀个误差的影响，那就只使⽤⼀个误差）。
3.2 输出层参数更新以权重参数w5为例，如果我们想知道w5对整体误差产⽣了多少影响，可以⽤整体误差对w5求偏导求出：（链式求导法则）现在我们来分别计算每个式⼦的值：计算：计算：（这⼀步实际上就是对sigmoid函数求导，⽐较简单，可以⾃⼰推导⼀下）计算：最后三者相乘：这样我们就计算出整体误差E(total)对w5的偏导值。
回过头来再看看上⾯的公式，我们发现：为了表达⽅便，⽤来表⽰输出层的误差：因此，整体误差E(total)对w5的偏导公式可以写成：如果输出层误差计为负的话，也可以写成：最后我们来更新w5的值：（其中，是learning rate，这⾥我们取0.5）3.3 隐含层参数更新计算：先计算：同理，计算出：两者相加得到总值：再计算：再计算：最后，三者相乘：为了简化公式，⽤sigma(h1)表⽰隐含层单元h1的误差：最后，更新w1的权值：Python代码：#coding:utf-8import randomimport math## 参数解释：# "pd_" ：偏导的前缀# "d_" ：导数的前缀# "w_ho" ：隐含层到输出层的权重系数索引# "w_ih" ：输⼊层到隐含层的权重系数的索引class NeuralNetwork:LEARNING_RATE = 0.5def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None): self.num_inputs = num_inputsself.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias)self.output_layer = NeuronLayer(num_outputs, output_layer_bias)self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):weight_num = 0for h in range(len(self.hidden_layer.neurons)):for i in range(self.num_inputs):if not hidden_layer_weights:self.hidden_layer.neurons[h].weights.append(random.random())else:self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])weight_num += 1def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):weight_num = 0for o in range(len(self.output_layer.neurons)):for h in range(len(self.hidden_layer.neurons)):if not output_layer_weights:self.output_layer.neurons[o].weights.append(random.random())else:self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])weight_num += 1def inspect(self):print('------')print('* Inputs: {}'.format(self.num_inputs))print('------')print('Hidden Layer')self.hidden_layer.inspect()print('------')print('* Output Layer')self.output_layer.inspect()print('------')def feed_forward(self, inputs):hidden_layer_outputs = self.hidden_layer.feed_forward(inputs)return self.output_layer.feed_forward(hidden_layer_outputs)def train(self, training_inputs, training_outputs):self.feed_forward(training_inputs)# 1. 输出神经元的值pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons)for o in range(len(self.output_layer.neurons)):# ∂E/∂zⱼpd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o])# 2. 隐含层神经元的值pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)for h in range(len(self.hidden_layer.neurons)):# dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼd_error_wrt_hidden_neuron_output = 0for o in range(len(self.output_layer.neurons)):d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h]# ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input()# 3. 更新输出层权重系数for o in range(len(self.output_layer.neurons)):for w_ho in range(len(self.output_layer.neurons[o].weights)):# ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼpd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)# Δw = α * ∂Eⱼ/∂wᵢself.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight# 4. 更新隐含层的权重系数for h in range(len(self.hidden_layer.neurons)):for w_ih in range(len(self.hidden_layer.neurons[h].weights)):# ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢpd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih)# Δw = α * ∂Eⱼ/∂wᵢself.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weightdef calculate_total_error(self, training_sets):total_error = 0for t in range(len(training_sets)):training_inputs, training_outputs = training_sets[t]self.feed_forward(training_inputs)for o in range(len(training_outputs)):total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o])return total_errorclass NeuronLayer:def __init__(self, num_neurons, bias):# 同⼀层的神经元共享⼀个截距项bself.bias = bias if bias else random.random()self.neurons = []for i in range(num_neurons):self.neurons.append(Neuron(self.bias))def inspect(self):print('Neurons:', len(self.neurons))for n in range(len(self.neurons)):print(' Neuron', n)for w in range(len(self.neurons[n].weights)):print(' Weight:', self.neurons[n].weights[w])print(' Bias:', self.bias)def feed_forward(self, inputs):outputs = []for neuron in self.neurons:outputs.append(neuron.calculate_output(inputs))return outputsdef get_outputs(self):outputs = []for neuron in self.neurons:outputs.append(neuron.output)return outputsclass Neuron:def __init__(self, bias):self.bias = biasself.weights = []def calculate_output(self, inputs):self.inputs = inputsself.output = self.squash(self.calculate_total_net_input())return self.outputdef calculate_total_net_input(self):total = 0for i in range(len(self.inputs)):total += self.inputs[i] * self.weights[i]return total + self.bias# 激活函数sigmoiddef squash(self, total_net_input):return 1 / (1 + math.exp(-total_net_input))def calculate_pd_error_wrt_total_net_input(self, target_output):return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_total_net_input_wrt_input();# 每⼀个神经元的误差是由平⽅差公式计算的def calculate_error(self, target_output):return 0.5 * (target_output - self.output) ** 2def calculate_pd_error_wrt_output(self, target_output):return -(target_output - self.output)def calculate_pd_total_net_input_wrt_input(self):return self.output * (1 - self.output)def calculate_pd_total_net_input_wrt_weight(self, index):return self.inputs[index]# ⽂中的例⼦:nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35, output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6) for i in range(10000):nn.train([0.05, 0.1], [0.01, 0.09])print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.09]]]), 9))#另外⼀个例⼦，可以把上⾯的例⼦注释掉再运⾏⼀下:# training_sets = [# [[0, 0], [0]],# [[0, 1], [1]],# [[1, 0], [1]],# [[1, 1], [0]]# ]# nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1])) # for i in range(10000):# training_inputs, training_outputs = random.choice(training_sets)# nn.train(training_inputs, training_outputs)# print(i, nn.calculate_total_error(training_sets))。
mlp模型原理MLP模型原理深度学习中的多层感知器（Multilayer Perceptron，MLP）是一种前馈神经网络，它由多个神经元层组成，每个神经元层与下一层之间存在全连接。
在MLP模型中，每个神经元接收前一层的输出，并通过一个非线性激活函数对其进行转换，然后将转换后的结果传递给下一层。
MLP模型的基本结构由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据，隐藏层负责对输入数据进行特征提取和转换，输出层则给出最终的预测结果。
隐藏层的数量和每个隐藏层中神经元的数量可以自行设定，根据问题的复杂程度和数据的特点来确定。
在MLP模型中，每个神经元的输出由以下几个部分组成：输入数据、权重、偏置和激活函数。
输入数据是前一层的输出结果，权重和偏置是模型的参数，激活函数则用于引入非线性变换。
通过调整权重和偏置，MLP模型可以学习到输入数据的复杂特征，并根据这些特征做出预测。
MLP模型的训练过程可以使用反向传播算法来实现。
反向传播算法通过计算模型的损失函数关于参数的梯度，然后使用梯度下降法更新参数，最小化损失函数。
在训练过程中，模型通过不断调整参数，逐渐提高对训练数据的拟合能力，从而实现对未知数据的预测能力。
MLP模型在深度学习中具有重要的地位，它可以应用于多种任务，如图像分类、语音识别、自然语言处理等。
在图像分类任务中，MLP模型可以从图像数据中提取特征，然后根据这些特征将图像分类到不同的类别。
在语音识别任务中，MLP模型可以将声音信号转换为文本信息，从而实现自动语音识别。
在自然语言处理任务中，MLP模型可以对文本数据进行分类、情感分析等。
然而，MLP模型也存在一些限制和挑战。
首先，MLP模型需要大量的训练数据才能取得好的效果，否则容易出现过拟合现象。
其次，MLP模型对输入数据的表示能力有一定的限制，无法处理像素之间的空间关系或序列数据中的时间关系。
此外，MLP模型训练过程中的计算量较大，需要较高的计算资源和时间成本。
多层感知机的层次模型多层感知机（MLP）是一种深度学习模型，属于前馈神经网络（Feedforward Neural Network）的一种。
MLP由输入层、隐藏层（可以有多层），和输出层组成。
每个层都包含多个神经元，神经元之间的连接有权重。
以下是多层感知机的层次模型：1.输入层（Input Layer）：•输入层是神经网络的第一层，负责接收原始数据特征。
•每个输入神经元对应输入数据的一个特征。
•输入层的神经元数目等于输入数据的特征数。
2.隐藏层（Hidden Layers）：•隐藏层位于输入层和输出层之间，是神经网络的核心组成部分。
•每个隐藏层包含多个神经元，神经元之间相互连接，连接带有权重。
•每个神经元在隐藏层中通过激活函数处理加权输入。
•多层表示隐藏层可以有多个，构成深度神经网络。
3.输出层（Output Layer）：•输出层位于神经网络的最后一层，负责产生网络的输出。
•输出层的神经元数量通常取决于任务的性质，例如二分类任务有一个神经元，多分类任务有多个神经元。
•输出层的每个神经元对应一个可能的类别或预测值。
4.权重和偏差（Weights and Biases）：•每个连接都有一个权重，用于调整输入的影响。
•每个神经元都有一个偏差（bias），用于调整神经元激活的阈值。
5.激活函数（Activation Functions）：•激活函数在神经元内部引入非线性性，允许网络学习复杂的映射。
•常见的激活函数包括ReLU（Rectified Linear Unit）、Sigmoid、和Tanh等。
多层感知机通过多个隐藏层的组合，可以学习到更复杂的特征和表示，使得模型能够适应更复杂的任务。
深度学习模型中的层次结构和权重参数通过反向传播算法进行训练，优化模型的预测能力。
多层感知器--MLP神经⽹络算法提到⼈⼯智能(Artificial Intelligence,AI),⼤家都不会陌⽣,在现今⾏业领起风潮,各⾏各业⽆不趋之若鹜,作为技术使⽤者,到底什么是AI,我们要有⾃⼰的理解.⽬前,在⼈⼯智能中,⽆可争议的是深度学习占据了统治地位,,其在图像识别,语⾳识别,⾃然语⾔处理,⽆⼈驾驶领域应⽤⼴泛.如此,我们要如何使⽤这门技术呢?下⾯我们来⼀起了解"多层感知器",即MLP算法,泛称为神经⽹络.神经⽹络顾名思义,就像我们⼈脑中的神经元⼀样,为了让机器来模拟⼈脑,我们在算法中设置⼀个个节点,在训练模型时,输⼊的特征与预测的结果⽤节点来表⽰,系数w(⼜称为"权重")⽤来连接节点,神经⽹络模型的学习就是⼀个调整权重的过程,训练模型⼀步步达到我们想要的效果.理解了原理,下⾯来上代码直观看⼀下:1.神经⽹络中的⾮线性矫正每个输⼊数据与输出数据之间都有⼀个或多个隐藏层,每个隐藏层包含多个隐藏单元.在输⼊数据和隐藏单元之间或隐藏单元和输出数据之间都有⼀个系数(权重).计算⼀系列的加权求和和计算单⼀的加权求和和普通的线性模型差不多.线性模型的⼀般公式:y = w[0]▪x[0]+w[1]▪x[1] + ▪▪▪ + w[p]▪x[p] + b为了使得模型⽐普通线性模型更强⼤,所以我们要进⾏⼀些处理,即⾮线性矫正(rectifying nonlinearity),简称为(rectified linear unit,relu).或是进⾏双曲正切处理(tangens hyperbolicus,tanh)############################# 神经⽹络中的⾮线性矫正 ########################################导⼊numpyimport numpy as np#导⼊画图⼯具import matplotlib.pyplot as plt#导⼊numpyimport numpy as py#导⼊画图⼯具import matplotlib.pyplot as plt#⽣成⼀个等差数列line = np.linspace(-5,5,200)#画出⾮线性矫正的图形表⽰plt.plot(line,np.tanh(line),label='tanh')plt.plot(line,np.maximum(line,0),label='relu')#设置图注位置plt.legend(loc='best')#设置横纵轴标题plt.xlabel('x')plt.ylabel('relu(x) and tanh(x)')#显⽰图形plt.show()tanh函数吧特征X的值压缩进-1到1的区间内,-1代表的是X中较⼩的数值,⽽1代表X中较⼤的数值.relu函数把⼩于0的X值全部去掉,⽤0来代替2.神经⽹络的参数设置#导⼊MLP神经⽹络from sklearn.neural_network import MLPClassifier#导⼊红酒数据集from sklearn.datasets import load_wine#导⼊数据集拆分⼯具from sklearn.model_selection import train_test_splitwine = load_wine()X = wine.data[:,:2]y = wine.target#下⾯我们拆分数据集X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=0)#接下来定义分类器mlp = MLPClassifier(solver='lbfgs')mlp.fit(X_train,y_train)MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,beta_2=0.999, early_stopping=False, epsilon=1e-08,hidden_layer_sizes=(100,), learning_rate='constant',learning_rate_init=0.001, max_iter=200, momentum=0.9,n_iter_no_change=10, nesterovs_momentum=True, power_t=0.5,random_state=None, shuffle=True, solver='lbfgs', tol=0.0001,validation_fraction=0.1, verbose=False, warm_start=False)identity对样本特征不做处理,返回值是f(x) = xlogistic返回的结果会是f(x)=1/[1 + exp(-x)],其和tanh类似,但是经过处理后的特征值会在0和1之间#导⼊画图⼯具import matplotlib.pyplot as pltfrom matplotlib.colors import ListedColormap#定义图像中分区的颜⾊和散点的颜⾊cmap_light = ListedColormap(['#FFAAAA','#AAFFAA','#AAAAFF'])cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF'])#分别⽤样本的两个特征值创建图像和横轴和纵轴x_min,x_max = X_train[:, 0].min() - 1,X_train[:, 0].max() + 1y_min,y_max = X_train[:, 1].min() - 1,X_train[:, 1].max() + 1xx,yy = np.meshgrid(np.arange(x_min,x_max, .02),np.arange(y_min,y_max, .02))Z = mlp.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z = Z.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:solver=lbfgs")plt.show()(1)设置隐藏层中节点数为10#设置隐藏层中节点数为10mlp_20 = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10])mlp_20.fit(X_train,y_train)Z1 = mlp_20.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z1 = Z1.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z1, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:nodes=10")plt.show()(2)设置神经⽹络有两个节点数为10的隐藏层#设置神经⽹络2个节点数为10的隐藏层mlp_2L = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10])mlp_2L.fit(X_train,y_train)ZL = mlp_2L.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊ZL = ZL.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, ZL, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:2layers")plt.show()(3)设置激活函数为tanh#设置激活函数为tanhmlp_tanh = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10],activation='tanh')mlp_tanh.fit(X_train,y_train)Z2 = mlp_tanh.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z2 = Z2.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z2, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:2layers with tanh")plt.show()(4)修改模型的alpha参数#修改模型的alpha参数mlp_alpha = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10],activation='tanh',alpha=1)mlp_alpha.fit(X_train,y_train)Z3 = mlp_alpha.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z3 = Z3.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z3, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:alpha=1")plt.show()总结: 如此,我们有4种⽅法可以调节模型的复杂程度: 第⼀种,调整神经⽹络每⼀个隐藏层上的节点数 第⼆种,调节神经⽹络隐藏层的层数 第三种,调节activation的⽅式 第四种,通过调整alpha值来改变模型正则化的过程 对于特征类型⽐较单⼀的数据集来说,神经⽹络的表现还是不错的,但是如果数据集中的特征类型差异⽐较⼤的话,随机森林或梯度上升随机决策树等基于决策树的算法的表现会更好⼀点. 神经⽹络模型中的参数调节⾄关重要,尤其是隐藏层的数量和隐藏层中的节点数. 这⾥给出⼀个参考原则:神经⽹络中的隐藏层的节点数约等于训练数据集的特征数量,但⼀般不超过500. 如果想对庞⼤复杂⾼维的数据集做处理与分析,建议往深度学习发展,这⾥介绍两个流⾏的python深度学习库:keras,tensor-flow⽂章引⾃ : 《深⼊浅出python机器学习》。
深度学习笔记二：多层感知机（MLP）与神经网络结构为了尽量能形成系统的体系，作为最基本的入门的知识，请参考一下之前的两篇博客：神经网络(一):概念神经网络(二):感知机上面的两篇博客让你形成对于神经网络最感性的理解。
有些看不懂的直接忽略就行，最基本的符号的记法应该要会。
后面会用到一这两篇博客中的一些记号和用法的约定什么的之后就不再啰嗦了。
一.基本结构看完上面给出的两个博客或者已经有基本概念的同学应该对于神经网络的基本结构有基本的认识了。
但是上面那个还只是涉及到单层结构，并没有推广到多层结构，同时，也没有在实践中使用这种结构的经验。
所以，这节的内容就是以手写体识别为例子来讲一下基本结构，和实践中的基本使用思想。
这是推广到更加复杂任务上的基础。
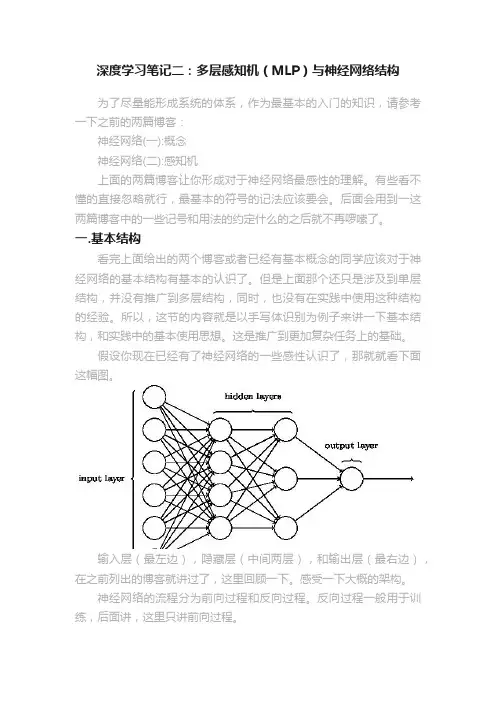
假设你现在已经有了神经网络的一些感性认识了，那就就看下面这幅图。
输入层（最左边），隐藏层（中间两层），和输出层（最右边），在之前列出的博客就讲过了，这里回顾一下。
感受一下大概的架构。
神经网络的流程分为前向过程和反向过程。
反向过程一般用于训练，后面讲，这里只讲前向过程。
还记得每个神经元上面都有对于一个输入的权值，以及一个偏置，还有一个激活函数。
（不知道的话看之前列出来的博客，后面不再强调了），所以一个前向过程的流程就是input输入，然后经过第一层神经元运算（乘上权值，加上偏执，激活函数运算一次），得到输出，然后第一层的输出作为第二层的输入，运算，得到第二层的输出…..直到到输出层运算，然后得到结果。
神经网络就是依靠这样一套机制来进行计算和预测的。
假如你的权值和偏置已经是被训练好了。
对于一个新的输入，进行这样的过程，就能够得到一个预测。
那么你就能够通过这个预测来解决一些问题了。
所以有机器学习思想的话，这些概念是很容易理解的。
而我们的任务就是找到权值和偏置这些参数的值，使得输出的东西让我们满意，达到我们的要求。
这里先补充一个思想：假如我们改变了某个神经元或者某几个神经元的权值或者偏置一点点，那么该神经元的输出肯定会变得不同，这些不同最终将反应在输出上面。
mlp计算权重MLP，即多层感知机（Multilayer Perceptron），是一种常见的人工神经网络模型，具有多个神经元层的结构。
它是一种前馈神经网络，通过学习输入和输出之间的关系，可以用于分类和回归问题。
在MLP中，每个神经元都与上一层的所有神经元相连，每个连接都有一个权重。
权重表示了不同神经元之间连接的强度，它决定了输入信号在神经网络中传递的影响力。
通过调整权重的数值，可以改变神经网络的行为，使其具备对不同输入的适应能力。
计算权重是指在训练神经网络时，通过使用某种算法来确定每个连接的权重值。
常用的计算权重的方法包括随机初始化、梯度下降和反向传播算法。
我们需要对神经网络进行初始化。
这一步通常是随机选择权重的初始值。
随机初始化可以使神经网络在训练过程中避免陷入局部最优解，提高其泛化能力。
接下来，我们需要定义一个损失函数，用于衡量神经网络输出与真实值之间的差距。
常见的损失函数包括均方误差（Mean Squared Error）和交叉熵损失（Cross Entropy Loss）等。
在计算权重的过程中，我们需要使用梯度下降算法。
该算法通过反复迭代来最小化损失函数。
在每一次迭代中，我们根据当前权重的数值计算损失函数的梯度，并更新权重的数值，使损失函数不断减小。
反向传播算法是梯度下降算法的一种变种，它通过从输出层向输入层传播梯度来计算权重的更新量。
具体来说，反向传播算法首先计算输出层的误差，然后逐层向后传播，计算每一层的梯度。
最后，根据梯度和学习率的设定，更新每个连接的权重。
除了梯度下降和反向传播算法，还有其他一些计算权重的方法。
例如，遗传算法可以通过模拟生物进化的过程来优化权重值。
此外，还有一些优化算法，如牛顿法和拟牛顿法，可以用于求解权重的最优值。
在计算权重的过程中，我们还需要注意一些问题。
首先，权重的数值过大或过小都可能导致神经网络无法正常工作，因此需要进行适当的权重初始化和正则化处理。
其次，过拟合是一个常见的问题，我们需要通过调整超参数和使用正则化技术来避免模型过于复杂。
mlp的层数和节点数确定方法
在机器学习中，多层感知器（MLP）是一种常见的神经网络模型。
确定MLP的层数和节点数是设计模型的关键部分，下面介绍几种确定方法。
1、经验法则：在实践中，我们可以根据经验法则来确定MLP的层数和节点数。
一般而言，对于简单的问题，我们可以使用一个或两个隐藏层，每个隐藏层的节点数可以根据训练数据的大小和复杂度进行调整。
2、交叉验证：交叉验证是一种常用的模型选择方法，可以通过交叉验证来确定MLP的层数和节点数。
将数据集划分为训练集和测试集，使用训练集训练不同层数和节点数的MLP模型，选择测试集上表现最好的模型。
根据测试集上的表现来确定最佳的层数和节点数。
3、网格搜索：网格搜索是一种寻找最佳超参数的方法，可以通过网格搜索来确定MLP的层数和节点数。
首先确定层数和节点数的范围，然后使用不同的参数组合训练不同的MLP模型，选择表现最好的模型。
根据表现最好的模型的层数和节点数来确定最佳的参数。
总之，在确定MLP的层数和节点数时，需要根据问题的复杂度和数据集的大小进行调整，并可以使用交叉验证和网格搜索等方法来寻找最佳的参数组合。
- 1 -。
mlp时间复杂度计算步骤概述及解释说明1. 引言1.1 概述在机器学习领域中，多层感知器（Multilayer Perceptron，简称MLP）是一类经典而重要的神经网络模型。
它由多个神经元组成的不同层次构成，通过前向传播和反向传播算法实现信息处理和模式识别。
研究人员广泛关注MLP的时间复杂度计算方法，因为它对于分析和改进网络性能具有重要意义。
1.2 文章结构本文将详细介绍MLP时间复杂度计算步骤及其解释说明。
文章分为以下几个部分：引言、MLP时间复杂度计算步骤、解释说明、结论和结束语。
1.3 目的本文的目的是系统总结MLP时间复杂度计算的方法并详细解释每个步骤，以帮助读者深入理解和应用时间复杂度分析在MLP中的作用。
同时，我们还将讨论MLP时间复杂度的影响因素以及未来可能的研究方向。
请耐心阅读接下来介绍部分建议留意内容，并对相关定义及背景进行了解。
2. MLP时间复杂度计算步骤2.1 MLP概述多层感知器（Multilayer Perceptron，简称MLP）是一种经典的人工神经网络模型，由输入层、隐藏层和输出层组成。
每一层都包含多个神经元节点，这些节点之间通过连接权重进行信息传递。
MLP是一种前馈神经网络，输入数据从输入层开始逐层向前传播，并通过激活函数计算每个神经元的输出。
MLP广泛应用于数据分类、模式识别和函数拟合等领域。
2.2 时间复杂度的重要性在设计和优化机器学习算法时，时间复杂度是一个关键指标。
它表示算法执行所需的时间随问题规模增长的趋势。
对于大规模数据集或复杂任务，高时间复杂度可能导致训练过程非常缓慢甚至不可行。
对于MLP模型来说，了解其时间复杂度可以帮助我们评估算法的效率，并优化网络结构和参数设置以提高训练速度。
2.3 MLP时间复杂度计算方法MLP的时间复杂度可以从两个方面考虑：前向传播和反向传播。
在前向传播中，我们需要将输入数据通过所有层的神经元进行计算，并输出最终的预测结果。
