当前位置：文档之家 › 高考数学试题分析及届高考备考建议立体几何与解析几何精品PPT课件

高考数学试题分析及届高考备考建议立体几何与解析几何精品PPT课件

  • 格式：ppt
  • 大小：1.01 MB
  • 文档页数：39

下载文档原格式

  / 39

合集下载

高考解析几何命题解读及精准备考(共32张PPT)

高考解析几何命题解读及精准备考(共32张PPT)
3
4c2 ，整理得 4c2 5ac a2
0，
即 4e2 5e 1 0 ，解得 e 1 或 e 1 （舍去）.故选 D. 4
直线方程的联立求交点坐标，将图形关系转化 为代数计算，突出解析几何中的解析两字
双曲线常见结论
椭圆常见结论
不要求全部都记，记住也不太现实要求学生会证明，记住一些常见的
文理相近姊妹题
考题研究
文20
利用焦点弦可以简化大部分运算
考题研究
1)圆锥曲线的解答题侧重椭圆、抛物线与直线位置关系的判断 及最值与范围的研究，定值定点问题探究；
2)直线的倾斜角，斜率及其直线方程的选择，圆的方程及几何 性质；
3)结合几何图形的性质与特征，圆锥曲线的定义求圆锥曲线的 轨迹；
考题研究
即 a 2, c 1b 3 ，所以点 E 的轨迹方程为： x2 y2 1 . 43
第1问学生要根据平面几何的知识，使数形结合的思想得以 体现，同时也考查了椭圆的定义.
（II）当直线 l 的斜率不存在时，直线 l 方程为 x 1 ， MN 3 ， PQ 8 ，此时四边形 MPNQ 面积为12 ； 当直线 l 的斜率存在时，设直线 l 的方程为 y k(x 1) ，与椭圆 x2 y2 1 联立得：
解析几何的定义是用代数的方法解决几何问题。首先这是几何问题， 涉及初中平面几何知识，平行全等相似各种图形性质，其次它又常 常用到其他的方法——解三角形、平面向量、函数导数最值、不等 式、方程，在坐标系中，点有坐标线有方程各类数据计算有公式， 这一部分也既是各类知识的交汇点，也是思想方法的集合地——函 数方程思想、数形结合思想、化归转化思想等，近几年常考常新的 标准方程、离心率、最值范围、距离、面积、角；轨迹问题、定点、 定值以及其他各种图形方程关系式的转化（数形结合思想与转化划 归思想的应用），我们在教学中应该引导学生对相关知识点进行分 析，找到他们之间的联系。将一些零散的几何知识形成相应的系统 性，这样能够在应用时更加娴熟，达到牵一发动全身的效果。

《高中数学立体几何》课件

《高中数学立体几何》课件
立体几何在数学、工程、建筑等领域 有着广泛的应用，是理解和描述现实 世界空间关系的重要工具。
立体几何的重要性
01
02
03
培养空间思维能力
学习立体几何有助于培养 学生的空间想象力和逻辑 思维能力，提高解决实际 问题的能力。
数学学科基础
立体几何是数学学科体系 中的重要组成部分，对于 理解数学概念、掌握数学 方法具有重要意义。
《高中数学立体几何》ppt课 件
目 录
• 立体几何简介 • 立体几何基础知识 • 立体图形的性质与分类 • 立体几何的应用 • 解题技巧与思路 • 立体几何的未来发展
01
立体几何简介
什么是立体几何
立体几何是研究三维空间中图形和物 体性质的一门学科。它涉及到点、线 、面、体等基本元素，以及它们之间 的位置关系和度量关系。
角度的计算
角度是描述两条射线或线段之间夹角 的大小的量。在立体几何中，角度可 以通过使用三角函数或几何定理来计 算。
距离的计算
距离是描述两点之间或一点到一条线 段之间的最短路径的大小的量。在立 体几何中，距离可以通过使用勾股定 理或几何定理来计算。
03
立体图形的性质与分类
立体图形的性质
空间性
立体图形存在于三维空间 中，具有空间特性。
近现代发展
随着数学和科学技术的不断进步， 立体几何逐渐与代数学、分析学等 学科交叉融合，形成了更加丰富和 深入的研究领域。
02
立体几何基础知识
点、线、面的基本性质
点的基本性质
面的基本性质
Байду номын сангаас
点是几何学中最基本的元素，没有大 小和形状。在空间中，点的唯一特征 是它的位置。
面是由无数条线组成的，它只有面积 而没有厚度。面的形状和位置由其上 的点和其上的线的分布决定。

高考数学 备考资料 解析几何专题研究课件(1)

高考数学 备考资料 解析几何专题研究课件(1)
内 容 2015年全国高考考试大纲要求
① 在平面直角坐标系中，结合具体图形，确定直线位置 的几何要素． ② 理解直线的倾斜角和斜率的概念，掌握过两点的直线 斜率计算公式． ③ 能根据两条直线的斜率判定这两条直线平行或垂直． ④ 掌握确定直线位置的几何要素，掌握直线方程的几种 形式（点斜式、两点式及一般式），了解斜截式与一次 函数的关系． ⑤ 能用解方程组的方法求两直线的交点坐标． ⑥ 掌握两点间的距离公式、点到直线的距离公式，会求 两条平行直线间的距离．
2012
2013 2014
2015
第 20 题 平面向量坐标运算、动点 轨迹、直线与抛物线相切、点线距 离公式 第 20 题 圆的方程、抛物线定义、 直线与抛物线位置关系、点到直线 距离公式、平行直线 第 20 题 圆的方程、 圆与圆的内切、 第 4 题 双曲线离心率、 渐近线等性质 椭圆定义、直线与圆相切、点线距 第 8 题 直线与椭圆相交的中点问题 离公式、直线与椭圆相交及弦长 第 4 题 双曲线焦点到渐近线距离 第 20 题 椭圆方程及几何性质、直 第 10 题 抛物线方程与性质、 向量数乘 线与椭圆相交问题及三角形面积 第 5 题 双曲线方程及焦点坐标、 平面 第 20 题 抛物线的切线、直线与抛 向量数量积坐标运算 物线的位置关系、相交问题的方程 第 14 题 椭圆方程与顶点等性质、圆 组及韦达定理 的标准方程
考试说明 具体要求
直 线 与 方 程
相同
一、2015年全国卷考试大纲与说明
内 容 圆 与 方 程
空 间 直 角 坐 标 系
2015年全国高考考试大纲要求 ① 掌握确定圆的几何要素，掌握圆的标准方程与一般方 程． ② 能根据给定直线、圆的方程，判断直线与圆的位置关 系；能根据给定两个圆的方程，判断两圆的位置关系． ③ 能用直线和圆的方程解决一些简单的问题． ④ 初步了解用代数方法处理几何问题的思想．

立体几何在高考中的命题分析-2023届高三数学一轮复习课件

立体几何在高考中的命题分析-2023届高三数学一轮复习课件
积函数的表达式，通过求导或不等式来求最பைடு நூலகம்！
由于 = 与 = ，底面正方形的边长相等，所以当 =
时，此时正四棱锥的底面积与高都是最小值，此时体积
取得最小值。


方法一
通过求导，判断函数的
单调性，来求最值
方法二
也可以通过三元的基本不
等式来求最大值
2、几何图形的内切球、外接球
（2020 年全国统一高考数学试卷（文科）
（2）夹角,距离问题；
（3）空间几何体的体积、表面积计算；
（4）空间几何体与球的组合体；
（5）立体几何与其它知识的交汇。
3、具体措施：
（1）抓源固本，把握通性通法
近年高考命题的一个显著变化是：由知识立意转为能力立意，在知识网络的交汇点处设计试
题，往往遵循大纲又不拘泥于大纲。但是，对高考试卷进行分析就不难发现，许多题目都能
（1）第一问突破原来的“证明”题型，改为考查“距离”
（2） 从以往由已知棱长求值的直接结构变为需要通过给出的
条件得出棱长再求值的间接结构，且隐性考查的空间中垂直关
系的证明不是特别容易；（该题的一个难点）
方法一
A1
C1
B1
D
E
M
几何法对学生的空间
想象能力要求较高，
是学生的一大弱点,
所以学生通常选择向
（2）理解空间中点、线、面的位置关系，能用空间中线面平行、垂直的有关性质与判定
定理进行证明；
（3）能用向量方法证明线线、线面、面面的平行和垂直；
（4）能用向量方法求解线线、线面、面面的夹角问题；
（5）能用向量方法求解点到直线、点到平面的距离问题。
2、关注考查热点：
（1）空间线线、线面、面面的平行和垂直问题；

高考复习立体几何ppt课件

高考复习立体几何ppt课件

（A） 有无数个 （B） 不能作出 （C） 只能作出一个 （D） 以上都有可能
BA
l
情况三
15
返回
例： 有以下四个命题： ① 若一条直线与另一条直线平行，则它就
与经过另一条直线的平面平行； ② 若一条直线垂直于一个平面的一条垂线，
则此直线平行于这个平面； ③ 若一条直线和一个平面内的两条直线都
垂直，则此直线必垂直于这个平面； ④ 平面内两条平行直线，若其中一条直线
求证：AC⊥面D1B1BD
D1
C1
பைடு நூலகம்A1
B1
D
C
O
A
B
40
返回
在正方体AC1中，O为下底面的中 心，B1H ⊥D1O, 求证：B1H⊥面D1AC
D1
C1
A1
H
B1
D
C
O
A
B
41
三垂线定理(逆) 复习：重要定理
如图，PA⊥平面，AO是平面的
P
斜线PO在平面内的射影， a
(1)若a⊥PO，则a⊥AO；
EH
∴ MN//CH
∴ MN //面BCE 22
返回
在正方体AC1中，O为平面ADD1A1的 中心，求证：CO // 面A1C1B
D1
C1
A1
B1
O
F
D
C
A
B
23
线面平行的性质
返回
(1)如果一条直线与一个平面平行， 则这条直线与这个平面无公共点
(2)如果一条直线与一个平面平行， 则这条直线与这个平面内的直线成 异面直线或平行直线
直线与平面 所成的角
定义
直线a、b是异面直线，经过空间任意 一点o，作直线a’、b’，并使a’//a， b’//b，我们把直线a’和b’所成的锐角 （或直角）叫做异面直线a和b所成的 角。

高考数学(理科)二轮专题透析课件专题五 立体几何(共199张PPT)ppt版本

高考数学(理科)二轮专题透析课件专题五 立体几何(共199张PPT)ppt版本

. 查空间几何体的结构特征、表面积与体积公式
三种题型都有可
. 能出现,在小题中常与三视图结合命题,也可能单独考查
角度 1:以三视图为背景考查几何体的表面积、体积
边长为
. 2
某空间几何体的三视图如图所示(图中小正方形的
1),则该几何体的侧面积是
【分析】 根据三视图的形状,把几何体放到正方体中还原
该几何体的形状,然后通过三视图的数据求解该几何体的侧面
2.用直观图给出几何体,先依据线面位置关系的判定定理与 性质定理讨论分析几何体的形状特征,再求体积或表面积.
《九章算术》是我国古代内容极为丰富
的数学名著,书中提到了一种名为“刍甍”的五面体(如图),平面
ABCD 为矩形,棱 EF∥AB.若此几何体中,AB=4,EF=2,△ADE 和△BCF
都是边长为 2 的等边三角形,则此几何体的表面积为(
|������|
量,M 为平面α内任意一点).
注意:
①求二面角时,两法向量的夹角有可能是二面角的补角,要 注意从图中分析二面角是钝角还是锐角.
②作辅助线(面)是立体几何证明题中常用技巧,作图时要依 据题设条件和待求(证)结论之间的关系结合有关定理作图.注意 线线、线面、面面平行与垂直关系的相互转化.
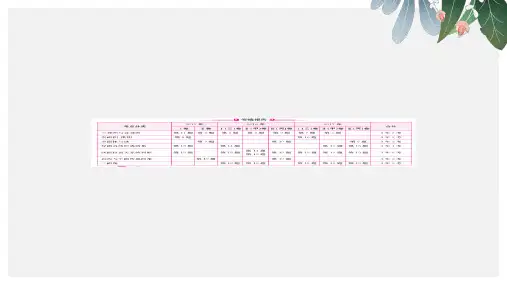
分析近三年的高考试题,立体几何部分在题型、题量、分值、
难度等方面,均保持相对稳定.在一套高考试题中,一般有 3 道立
体几何题,其中小题 2 道,解答题 1 道,分值 22 分,约占总分(150
分)的 15%.三视图与体积表面积的结合、空间垂直与平行的证明、
求空间角仍然是命题的热点,单纯的考查多面体体积的计算、多 面体与球的切接问题、折叠与展开问题、线面位置关系的判断也

人教版高中数学必修立体几何复习课件(共102张PPT)


1 1
1
11.已知某个几何体的三视图如图2，根据图中标出的尺寸 （单位：cm），可得这个几何体的体积是_____8_0__0.0 cm 3
3
2 0 20
主视图
10
10
2 俯0视图
2 侧0视图
第二章 点、直线、平面之间的位置关系
• 四个公理
直线与直线位置关系 • 三类关系 直线与平面位置关系
平面与平面位置关系
（3）
a a
// b
b
（较常用）；
（4）
a
//
a
；
（5）
a a
b
a
（面面垂直 线面垂直）
a b
4.面面垂直
向的侧视图（或称左视图）为（
A
A
H
G
Q
B
C
侧视 B
）A
C
I
P
E
图1
F
B
D
E
D
图2
F
B
B
B
E A．
E B．ቤተ መጻሕፍቲ ባይዱ
E C．
E D．
练习10：(1)如图是一个空间几何体的三
视图，如果直角三角形的直角边长均为
正视图 侧视图
1，那么几何体的体积为( ) C
A．1 B．1 C． 1 D．1
俯视图
2
3
6
V1 3S底 h1 31111 3
②判定定理：如果一个平面内的两条相交直线都平行于 另一个平面，那么两个平面互相平行；
符号表述： a,b , a b O, a //,b // //
//
③面面平行的性质定理：
a
a
//

高考解析几何复习专题 ppt课件


A，B 两点， 交 C 的准线于 P，Q 两点．
（I）若 F 在线段 AB 上， R 是 PQ 的中点，证明 AR FQ ；
面平 积行 表特 示征
（II）若 PQF 的面积是 ABF 的面积的两倍，求 AB 中点的轨迹方程.
注：设直线方程与点坐标
2016－Ⅲ－文
典型题例（设直线方程）
题
（1） C : y2 2x, F (1 ,0) ，准线方程： x 1
0
x1x2
y1 y2
0
6、中点或对称关系：
7、其他位置关系：
常见关联数形特征--翻译转换
量
8、线段长度或弦长:距离公式或弦长公式
值
9、三角形(或四边形)面积：
S
1 2 ldl
1 2
m|
x1
x2
|
1 2
mn sin
关
系
10、量值关系：平方关系、倒数关系、倍值关系等
11、向量关系：向量模或向量的线性关系
m)( k x2
m)
k 2 x1x2
k m( x1
x2 )
m2
3(m2 4k 3 4k 2
2)
由： OAOB
3 2
，所以
x1x2
y1 y2
3 2
，
4(m2 3) 3(m2 4k 2 ) 3 7m2 12k 2 12 3
3 4k 2 3 4k 2
2
3 4k 2
2
又： m2 1 k 2
过点p且垂直于oq的直典型题例关联特征转换非交点法应用题例数学语言转换数形特征转换圆锥曲线概念与基本量关系向量与数量关系转换已知点ab是椭圆的左右顶点f为左焦点点p是椭圆上异于ab的任意一点直线ap与过点b且垂直于x轴的直线交于点m直线bpmn1求证

解析几何专题分析与备考策略课件-2025届高三数学一轮复习


客观题直线与圆的考查
2021 年高考新Ⅰ卷
●研究命题考查意图---知道为什么考(一核)
11.已知点 P 在圆 x 52 y 52 16 上,点 A4,0 、 B0, 2 ,则（ ）
【课标要求】
能够掌握平面解析几 何解决问题的基本过程:
根据具体问题情境的 特点建立平面直角坐标系;
根据几何问题和图形 的特点，用代数语言把几 何问题转化成为代数问题;
根据对几何问题(图形) 的分析，探索解决问题的 思路，运用代数方法得到 结论，给出代数结论合理 的几何解释，解决几何问 题.
【学业要求】
2020（山东）
2021新Ⅰ
2022新Ⅰ
2023新Ⅰ
1
2
3
近三年以中难为主
单4 选5
椭圆的定义与基本不等式
椭圆的性质离心率
6
直线与圆、三角变换
7
8
9 曲线的方程
多 10 选 11
直线与圆的位置关系 抛物线与直线（与函数综合）
12
13 抛物线与直线
填 14 空 15
抛物线的方程
圆与圆关系性质
16
椭圆的性质定义
一、新高考Ⅰ卷考查情况统计分析 考察题型一般以“三小一大”为主，分值27分.
单选 多选 填空 解答
全国新高考Ⅰ卷知识点明细
2020年
2021年
2022年
9
5
11
11
13
14
14、16
22
21
21
2023年 5、6
16 22
明确考题与考点
综合性，每个题目考查多个知识点
高考试题考情分析 客观题位置
1.能够掌握平面解析几何解决问题的基本过程 ①根据具体问题情境的特点，建立平面直角坐标系; ②根据几何问题和图形的特点，用代数语言把几何问题 转化成为代数问题； ③根据对几何问题(图形)的分析，探索解决问题的思路; ④运用代数方法得到结论; ⑤给出代数结论合理的几何解释，解决几何问题. 2.能够根据不同的情境，建立平面直线的方程，建立椭 圆、抛物线、双曲线的标准方程，能够运用代数的方法 研究上述曲线之间的基本关系，能够运用平面解析几何 的思想解决一些简单的实际问题. 解析几何研究的问题: ①根据条件求曲线的方程:②根据曲线方程研究性质.

2019年全国高考数学解析几何部分试题分析和复习建议(共28张PPT)


| MF1 | exM
a

2 3
xM
+6=8
，所以
xM
3 ，所以 M 的坐标为 (3,
15) .
21．（理）已知曲线 C：y= x2 ，D 为直线 y= 1 上的动点，过 D 作 C 的两条切线，切点分
2
2
别为 A，B.
（1）证明：直线 AB 过定点：
（2）若以 E(0， 5 )为圆心的圆与直线 AB 相切，且切点为线段 AB 的中点，求四边形 2
⋯⋯①
由 0 ，可得 k2 2kt 1 0 ⋯⋯②
于是 k1 k2 2t ， k1k2 1，
将②代入①得，
A(k1
,
k12 2
)
，
B(k2
,
k22 2
)
，
所以 kAB

k1 k2 2
t
.
故直线 AB 的方程为 y k1 k2 x 1 ，即直线 AB 过定点 (0, 1 ) .
因此，四边形 ADBE 的面积为 3 或 4 2 .
法二：由（1）得 | x1 x2 | (x1 x2 )2 4x1x2 4t2 4 ，
把 x t 代入 y tx 1 得， y t2 1 .
2
2
则四边形 ADBE 的面积
S

SABD
SABE

1 2
由 EM AB ，得 t t(t 2 2) 0 ，得 t 0 或 t2 1，
故四边形 ADBE 的面积为 3 或 4 2 .
法三：设 AB 的中点为 G，则G
������1+������2 , ������1+������2 ,������������ =
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（二）解答题部分 1.2011年高考试题展示
（1）山东卷
本题主要考查四棱台中的结构特征、余弦定理、线线垂直与 线面平行的垂直，以及空间想象能力与逻辑推理能力.
本题主要考查空间几何体的结构特征、空间线 面平行的证明与二面角的求解，以及空间想象 能力与逻辑推理能力.
本题涉及到空间组合体的体积求解.
（2）新课标
本题主要考查四棱锥的结构特征以及空间中线线垂直的证 明以及棱锥高的求解.
本题主要考查四棱锥的结构特征以及线线垂直的证明与二面角 的求解.
文理使用同一个锥体作为载体.
（3）全国卷
本题主要考查四棱锥中的线面垂直证明以及线面角的求解.
（4）上海卷
本题主要考查正四棱柱的结构特征以及线面角、二面角的求解、 点到面的距离与棱柱中的基本运算.
本题主要考查正四棱柱的结构特征以及异面直线所成角与几何 体体积的求解.
2.2007-2010四年高考试题统计
2.2007-2011四年高考试题统计
3.高考试题研究及命题趋势分析
[1]山东卷 从近几年高考试题来看，几何体按照柱体和锥体交替出现 的规律，但近几年的高考试题中，台体与不规则几何体成 为命题的载体；文科以空间线面平行与垂直的证明、锥体 体积的求解为命题重点；理科第1问均为空间线面关系的 证明——多为线面平行的证明，第2问命题的热点是二面 角的求解，并且根据几何体的结构特征很容易建立空间直 角坐标系，将二面角的求解转化为空间向量的有关运算.
备考建议
1. 研究“两纲一题一材”即考纲、大纲与高考试题以 及新教材,把握好复习的方向. 2.夯基础,抓落实，促规范
基础知识、基本技能、基本方法、基础练习要到位, 立体几何的基本概念、公理、定理是基础;解题步骤要 规范;注重通性通法, 在日常教学中要将落实进行到底. 3.注重数学方法，加强学法指导
命题的趋势与预测： （1）命题的载体逐步趋向不规则几何体，有意识地加强对 空间几何体结构特征的认识和空间想象能力的考查； （2）几何载体也趋向文理有别； （3）在空间线面关系的证明过程中渗透空间几何体中的一 些基本运算； （4）试题的位置在19题左右摆动； （5）注意几何体中的一些运算在其它问题中的渗透，如 2011年山东卷中的应用题就是以几何体体积的计算为背景， 考查函数建模以及导数在实际问题中的应用. 预计2012年的山东高考命题中，总体上试题的难度基本保持 不变，命题的几何载体可能为不规则的几何体（或组合体）， 文科仍会坚持以空间线面关系的推理证明、几何体的体积求 解为主；理科坚持以空间线面关系的推理证明与二面角的求 解为主.
（2）新课标试卷分析： 2007年有两道客观题，一道考查三视图与几何体的求解，一 道考查柱体、锥体、球的组合体体积； 2008年有两道客观题，文理均不同，一道题目基本相同，考 查球内接六棱柱以及球的体积；一道文理不同的试题，其中 文科考查线面平行与垂直的判断，理科考查几何体与三视图 有关最值； 2009年有两道客观题，一道通过三视图求棱锥的全面积，文 理相同；一道是在正方体中文理关于线面关系、几何体体积 等不同命题的判断； 2010年有两道客观题，两道试题均不同，一道考查球的组合 体以及球的表面积计算；一道考查简单几何体三视图的了解.
本题主要考查几何体的结构特征和三视图的识别.A
（2）新课标全国卷（理6文8）在一个 几何体的三视图中，正视图和俯视图 如右图所示，则相应的俯视图可以为
本题主要考查三视图的识别以及彼此之间的关
系.D
23
本题主要考查球内接四棱锥及其体积求解. 3
本题主要考查球内接圆锥及其体积的计算.
（3）全国卷
本题主要考查二面角中的基本计算以及点到面的距离求解.C 本题主要考查二面角中的基本计算.C 本题考查球得截面的性质以及二面角的应用.B
（3）全国卷
本题主要考查正方体中二面角的求解. 本题主要考查正方体中异面直线所成角的求解.
（3）上海卷
本题主要考查圆锥的侧面积与体积的计算. 本题主要考查圆锥的三视图及其侧面积的计算.
2.2007——2010四年高考试题统计（客观题部分）
2.2007——2010四年高考试题统计（客观题部分）
<2>新课标卷
试卷多以锥体为载体考查空间线面关系的逻辑 推理以及空间角与距离的求解，只有2008年的 高考试题以正方体为载体；并且文理几何体载 体也基本相同，只有2009年的试题中文理几何 体的载体不同.试题多为两问：（1）问均为空 间线面关系的证明，文、理科均以垂直关系的 证明为命题的重点；（2）问文科差别明显， 文科以几何体（多为锥体）体积的求解为命题 重点；而理科线面角而二面角的求解平分天下.
转化、化归的思想贯穿立体几何的始终，是处理立
体几何问题的基本思想．另外还要注意提高识图、理 解图、应用图的能力，解题时应多画、多看、多想， 这样才能提高空间想象能力和解决问题的能力． 4.合理建立坐标系，突出向量方法
2011年高考试题分析及备考建议
立体几何与解析几何部分
高密教科院
立体几何部分
（一）客观题部分
1.2011年山东卷、全国课标卷、全国卷、上海卷客观题展示
（1） 山东卷（文、理11）下图是长和宽分别相 等的两个矩形．给定下列三个命题： ①存在三棱柱，其正(主)视图、俯视图如下图； ②存在四棱柱，其正(主)视图、俯视图如下图； ③存在圆柱，其正(主)视图、俯视图如下图． 其中真命题的个数是 (A)3 (B)2 (C)1 (D)0
ቤተ መጻሕፍቲ ባይዱ.高考命题研究及命题趋势分析
（1）山东近五年来立体几何客观题的考查，每年都有所变化： 2007年1道选择题，主要考查简单几何体的三视图的识别； 2008年1道选择题，主要考查球与圆柱组合体的三视图及其表面 积的求解； 2009年2道选择题，一道考查棱锥、圆柱的组合体的三视图与体 积的求解；一道考查线面垂直与充要条件的判断相结合； 2010年1道选择题，主要考查空间线面位置关系判定与性质. 命题的趋势与预测：试题的难度逐步降低，几何体的结构特征与 三视图的识别是命题的热点，空间线面关系的判断往往与充要条 件的判断相结合. 预计2012年的山东高考命题中，立体几何的客观题仍然只有一道， 命题的重点应为简单几何体的三视图与几何体的表面积、体积相 结合.