2016全国大学生数学建模竞赛培训(MATLAB)
- 格式:ppt
- 大小:2.34 MB
- 文档页数:102

全国大学生数学建模竞赛颁发MATLAB创新奖
近日,第18 届全国大学生数学建模竞赛于天津举行颁奖大会,对本次竞赛的优秀组织及参赛队伍进行了肯定和鼓励。
大会同时宣布,通过对全国一等奖获奖名单的甄选,组委会向本科组的中南大学队(魏太云、詹德坚、刘诗琴)和专科组的江西应用技术职业学院队(朱诗馨、叶骏、承姿辛)颁发
MATLAB 创新奖,以表彰这两组队伍在比赛过程中的创新性。
这也是该竞赛
在全国范围内首次创立并颁发该奖项。
中南大学队针对的问题是“眼科病床的合理安排”,旨在通过数学建模来帮助解决某眼科医院住院部的病床合理安排问题,以提高对医院资源的有效利用。
江西应用技术职业学院队则选择了“卫星和飞船的跟踪监控”题目,利用模型来
分析卫星或飞船的测控情况并解决测控站数目、测控范围等方面的问题。
医院就医排队是大家都非常熟悉的现象,无论患者是就诊、划价,还是取药等,往往需要排队,因此如何合理利用医院资源非常重要。
而卫星和飞船作为国民经济和国防建设中的重要支柱,对它们的发射和运行过程进行测控也是航天系统的一个重要组成部分。
由此可见,小到关注民生的住院问题,大到国家安防的航天领域,都离不开数学建模的应用。
这两组队伍在竞赛过程中不仅表现出了扎实的技术知识和良好的团队合作精神,而且充分体现了他们的创新思维,这也是他们之所以能获得MATLAB 创新奖的原因。
众所周知,近半个多世纪以来, 随着计算机技术的迅速发展,数学建模正逐渐从纯竞赛和科研领域转向应用领域,并以空前的广度和深度向国防、航空航天、金融、生物、医学、环境、地质等行业渗透,因此,能够运用数学知识解决复杂跨学科问题的复合型人才已经成为企业优先考虑的培养对象。
而另一方。
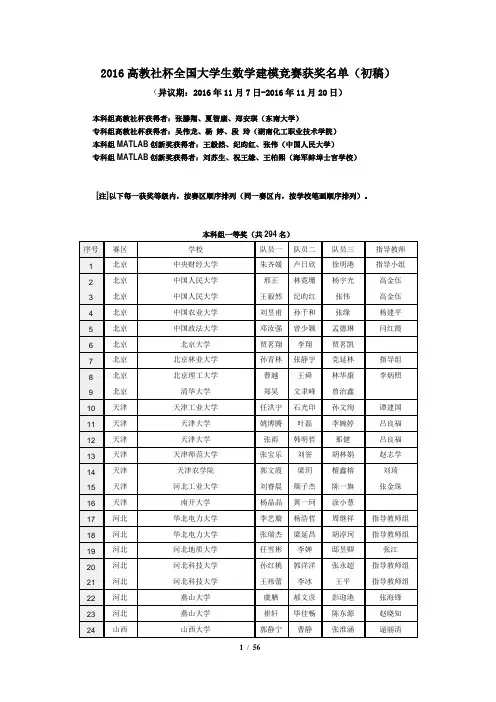
2016高教社杯全国大学生数学建模竞赛获奖名单(初稿)(异议期:2016年11月7日-2016年11月20日)
本科组高教社杯获得者:张滕翔、夏智康、郑安琪(东南大学)
专科组高教社杯获得者:吴伟龙、杨婷、段玲(湖南化工职业技术学院)
本科组MATLAB创新奖获得者:王毅然、纪昀红、张伟(中国人民大学)
专科组MATLAB创新奖获得者:刘苏生、祝王缘、王柏熙(海军蚌埠士官学校)
[注]以下每一获奖等级内,按赛区顺序排列(同一赛区内,按学校笔画顺序排列)。
本科组一等奖(共294名)
本科组二等奖(共1621名)
曹小
专科组一等奖(共60名)。
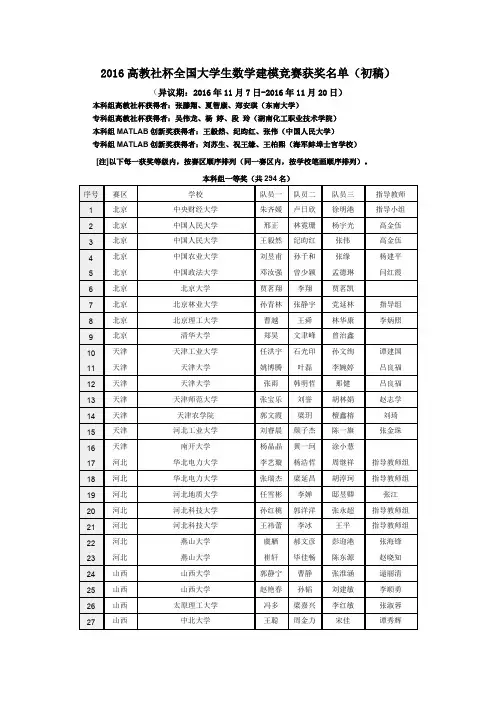
2016高教社杯全国大学生数学建模竞赛获奖名单(初稿)(异议期:2016年11月7日-2016年11月20日)
本科组高教社杯获得者:张滕翔、夏智康、郑安琪(东南大学)
专科组高教社杯获得者:吴伟龙、杨婷、段玲(湖南化工职业技术学院)
本科组MATLAB创新奖获得者:王毅然、纪昀红、张伟(中国人民大学)
专科组MATLAB创新奖获得者:刘苏生、祝王缘、王柏熙(海军蚌埠士官学校)
[注]以下每一获奖等级内,按赛区顺序排列(同一赛区内,按学校笔画顺序排列)。
本科组一等奖(共294名)
本科组二等奖(共1621名)
曹小
专科组一等奖(共60名)。




电池剩余放电时间预测摘要铅酸电池的剩余放电时间是电池性能指标中的一个重要参数,对电池的输出性能和使用寿命有着至关重要的影响。
但是在生活中不免遇到电池用完了却没有备用电池的情况,而且电池的使用时间在我们生活中与我们息息相关,有时候这会给我们的生活造成很大的困扰。
本文就是对电池剩余电量和放电时间的矛盾进行讨论得出一个相对准确的电池剩余放电时间预测的一个模型的建立。
针对问题一:电池的剩余放电量这一问题。
首先,根据题目我们得知铅酸电池在放电过程中电流时恒定的,并且铅酸电池的额定保护电压是9V ,我们根据{附件一}给出的数据进行分析,然后利用MATLAB 软件进行图像拟合,得到一个电压与时间的放电曲线图,并且,根据MATLAB 软件拟合得出的图像,经过figure 对图像的精确处理,最终得出初等函数来表示各放电曲线。
又根据平均相对误差定义得出:平均相对误差(MRE 是预测误差相对值的平均值,其计算公式为:)'|i i |1j j j j MRE n i -=∑根据公式和附件一中给出的数据按照比例筛选出231组数据【附件二】,并对数据进行处理,我们分别求出各放电曲线的平均相对误差。
并且根据测得电压都为9.8V 时,根据模型得出电池剩余放电时间分别是多少。
针对问题二:根据数据拟合的曲线图像得出三种情况进行讨论。
用初等函数表示A20-A100的放电曲线,并根据放电曲线的平均相对误差。
然后分别求出它们剩余放电时间。
然后我们利用求平均数的方法大概绘制出55A 的曲线图。
针对问题三:根据附件2中的数据,利用Excel 表格数据整理得出图形【附件三】,分析并计算得出模型1、模型2,通过优化得出模型3。
由于同一电池在不同衰减状态下,在同一电流强度情况下从充满电开始放电,时间随电压不断变化,所以我们从电压方面进行具体分析。
一.问题重述铅酸电池作为电源被广泛用于工业、军事、日常生活中。
在铅酸电池以恒定电流强度放电过程中,电压随放电时间单调下降,直到额定的最低保护电压(Um )。




用方格因子影响模型探究小区开放对道路通行的影响摘要目前我国人口增长,各种大型小区增多,各小区家庭拥有小汽车量也在增多,根据我国的道路交通设计和城市规划设计,我国的道路交通存在着严重问题,所以对交通的通行能力有着较大需求,本题将要分析的是,如果常规的封闭性小区开放,那周边道路通行会出现怎样的变化。
关于第一问,本文选取五个交通参数,道路通行能力、道路网的饱和度、车道交通流量比、车辆的延误时间、饱和流量;可以由各个指标来衡量小区开放以后对周围道路的交通状况的影响。
关于第二问,先将城市交通道路网格化,再建立方形小区内点对之间的最优路径寻模型,通过分析交通网格化下的封闭性小区开放之后,小区内的各个点对之间的各个路径中,最优路径是否存在,同时可以计算得出小区的面积及位置对点对间交通便捷度影响因子的影响,通过因子分析法来计算并寻找最优路径,从而判断周边道路的交通状态,是否会因为小区的开放而得到缓解。
关于第三问,分析其开放前后小区对周边道路的交通通行带来的影响;从参考资料中选取一个城市小区,通过对小区结构以及道路结构对其道路通行能力的分析。
同时构建一个方形小区,通过假设其开放前和开放后的各类数据,进行一个辅助比较,通过这两种类型的小区,并应用第一问与第二问中的模型,发现打破一个封闭小区,可以使得周边道路上车辆的通行能力增加,即使得交通状况有所改善。
第四问要求从交通通行的角度提出建议,通过以上三问对开放性小区评价指标、周边道路交通体系、长沙市某具体小区与构建的虚拟小区等的研究结果,向相关部门提出了对小区开放的合理建议。
关键字:小区开放;道路通行能力;最优路径;饱和流量;交通便捷度影响因子一、问题重述近几年,我国经济飞速发展,在GDP上升的同时,封闭型的小区也越来越多,政府、开发商、居民等也越来越多的居住于封闭型小区,同时私家车在我国城市居民家庭中的数量越来越多,逐步普及。
这给各个道路的交通,以及小区周边的道路交通造成了巨大压力,可以说城市道路交通拥堵的问题变得不容忽视。