扫描线种子填充算法

程序代码
PointTemp.x=xleft;PointTemp.y=PointTemp.y-2; //处理下一条扫描线 while(PointTemp.x<xright) { bSpanFill=FALSE; while(pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=BoundaryClr && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=SeedClr) { bSpanFill=TRUE; PointTemp.x++; } if(bSpanFill) { if(PointTemp.x==xright && pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y))!=BoundaryClr && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=SeedClr) PopPoint=PointTemp; else PopPoint.x=PointTemp.x-1;PopPoint.y=PointTemp.y; Push(PopPoint); bSpanFill=FALSE; } while((pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))==BoundaryClr && PointTemp.x<xright) || (pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) ==SeedClr && PointTemp.x<xright)) PointTemp.x++; } }

实验2：多边形区域扫描线填充或种子填充计科102 蓝广森 1007300441一、实验目的通过实验，进一步理解和掌握几种常用多边形填充算法的基本原理掌握多边形区域填充算法的基本过程掌握在C/C++环境下用多边形填充算法编程实现指定多边形的填充。

二、实验内容及要求实现多边形区域扫描线填充的有序边表算法，并将实现的算法应用于任意多边形的填充，要求多边形的顶点由键盘输入或鼠标拾取，填充要准确，不能多填也不能少填。

要求掌握边形区域扫描线填充的有序边表算法的基本原理和算法设计，画出算法实现的程序流程图，使用C或者VC++实现算法，并演示。

三、实验原理种子填充算法又称为边界填充算法。

其基本思想是：从多边形区域的一个内点开始，由内向外用给定的颜色画点直到边界为止。

如果边界是以一种颜色指定的，则种子填充算法可逐个像素地处理直到遇到边界颜色为止。

种子填充算法常用四连通域和八连通域技术进行填充操作。

四向连通填充算法：a）种子像素压入栈中；b）如果栈为空，则转e)；否则转c)；c）弹出一个像素，并将该像素置成填充色；并判断该像素相邻的四连通像素是否为边界色或已经置成多边形的填充色，若不是，则将该像素压入栈；d）转b）；e）结束。

扫描线填充算法的基本过程如下：当给定种子点(x,y)时，首先填充种子点所在扫描线上的位于给定区域的一个区段，然后确定与这一区段相连通的上、下两条扫描线上位于给定区域内的区段，并依次保存下来。

反复这个过程，直到填充结束。

区域填充的扫描线算法可由下列四个步骤实现：(1)初始化：堆栈置空。

将种子点(x,y)入栈。

(2)出栈：若栈空则结束。

否则取栈顶元素(x,y)，以y作为当前扫描线。

(3)填充并确定种子点所在区段：从种子点(x,y)出发，沿当前扫描线向左、右两个方向填充，直到边界。

分别标记区段的左、右端点坐标为xl和xr。

(4)并确定新的种子点：在区间[xl，xr]中检查与当前扫描线y上、下相邻的两条扫描线上的象素。

72 8，9，4，7，9。

/* 4-connected flood-fill*/void FloodFill4(int x,int y,int fillColor,int oldColor){int current;current = GetPixel(x, y);if (current == oldColor){SetPixel(x, y, fillColor);floodFill4(x+1, y, fillColor, oldColor);floodFill4(x-1, y, fillColor, oldColor);floodFill4(x, y+1, fillColor, oldColor);floodFill4(x, y-1, fillColor, oldColor);}}图3-33 四连通泛填充算法的C语言实现图3-34 简单的种子填充算法的填充实例从图3-34（b）可知，某些像素被多次压入堆栈，而且算法所需的堆栈空间较大，堆栈深度也比较深，而且因为每次递归调用只填充一个像素，所以算法的效率也比较低。

如果待填充的区域较大，区域内包含的像素较多，不仅填充速度慢，更重要的是很可能会导致堆栈溢出，这是种子填充算法的致命弱点。

能否利用扫描线的连贯性，每次递归调用填充一行像素，并同时减少压入堆栈的像素数目呢？答案是肯定的，这就是所谓的扫描线种子填充算法。

3.4.6 扫描线种子填充算法扫描线种子填充算法（Scan Line Seed Fill Algorithm）采用使堆栈尺寸极小化即减少压入堆栈的像素数目的方法，就是在任意一段连续的扫描线区段内只取一个像素作为种子像素压入堆栈。

该算法的描述如下。

（1）种子像素入栈。

（2）当栈为非空时，重复执行以下步骤。

①栈顶像素出栈。

②沿扫描线对出栈像素的左右像素进行填充，直到遇到边界像素为止。

③将上述区间内最左、最右像素记为x left和x right。

④在区间[x left, x right]内检查与当前扫描线相邻的上下两条扫描线是否全为边界像素或已填充的像素，若为非边界和未填充，则把每一区间的最右像素x right作为种子像素压入堆栈，重复执行步骤（2）。

2.1 深度递归的种子填充算法
2.2 扫描线种子填充算法
2.1 深度递归的种子填充算法
种子填色又称边界填色(Boundary Filling)。 它的功能是，给出多边形光栅化后的边界位置及边 界色代码oundary_color，以及多边形内的一点(x, y)位置，要求将颜色fill_color填满多边形。
动画演示
扫描线种子填充算法特点
1. 该算法考虑了扫描线上象素的相关性，种子象 素不再代表一个孤立的象素，而是代表一个尚 未填充的区段。 2. 进栈时，只将每个区段选一个象素进栈（每个 区段最右边或最左边的象素），这样解决了堆 栈溢出的问题。 3. 种子出栈时，则填充整个区段。 4. 这样有机的结合：一边对尚未填充象素的登记 （象素进栈），一边进行填充（象素出栈）， 既可以节省堆栈空间，又可以实施快速填充。

3. 已知有一个5边形如下。建立新边表 NET，并写出每一条扫描线经过时活性边 表AET中的数据状态。
X ΔX Ymax
第1项存当前扫描线与边的交点坐标x值； 第2项存从当前扫描线到下一条扫描线间x的增量Dx; 第3项存该边所交的最高扫描线号ymax； 第4项存指向下一条边的指针。
假定当前扫描线与多边形某一条边的交点的x 坐标为x，则下一条扫描线与该边的交点不要重计 算，只要加一个增量△x。(连贯性) 设该边的直线方程为：ax+by+c=0； 若y＝yi，x=x i；则当y = y i+1时， x i+1=xi-b/a 其中ΔX= -b/a为常数， 另外使用增量法计算时，我们需要知道一条边 何时不再与下一条扫描线相交，以便及时把它从 活性边表中删除出去。
建立或调整AET(ActiveEdgeList)；

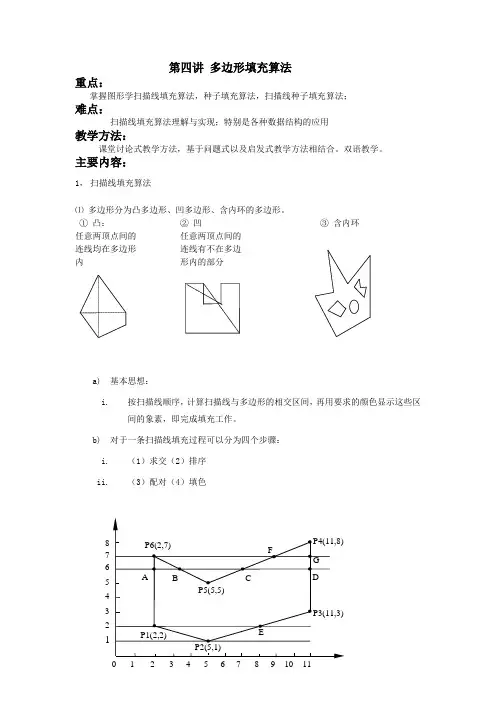
第四讲 多边形填充算法重点：掌握图形学扫描线填充算法，种子填充算法，扫描线种子填充算法；难点：扫描线填充算法理解与实现；特别是各种数据结构的应用教学方法：课堂讨论式教学方法，基于问题式以及启发式教学方法相结合。

双语教学。

主要内容：1， 扫描线填充算法⑴ 多边形分为凸多边形、凹多边形、含内环的多边形。

① 凸： ② 凹③ 含内环 任意两顶点间的 任意两顶点间的连线均在多边形 连线有不在多边内 形内的部分a) 基本思想：i. 按扫描线顺序，计算扫描线与多边形的相交区间，再用要求的颜色显示这些区间的象素，即完成填充工作。

b) 对于一条扫描线填充过程可以分为四个步骤：i.（1）求交（2）排序 ii.（3）配对（4）填色12345678② 步骤· 求交：计算扫描线与多边形各边的交点；· 排序：把所有交点按x 值递增顺序排序；· 配对：12，34，…，交点两两配对；· 填色：把交点对的象素置成多边形颜色，把交点对以外的象素置成背景色。

③ 活性边表算法：处理每一条扫描线时，仅计算和它相交的多边形的边· 活性边：当前扫描线与多边形相交的边；· 活性边表：存放扫描线与活性边交点(按X 递增顺序)的一张链表；8节点：第1项存当前扫描线与边的交点坐标x 值；第2项存从当前扫描线到下一条扫描线间x 的增量∆x ；第3项存边所交的扫描线的y max④ 算法· 增量法：令当前扫描线与多边形某一条边的交点的x 坐标为x ，则下一条扫描线与该边的交点不要重计算，只要加一个增量。

该边的直线方程为：ax+by+c=0；若y ＝y i ，x=x i ；则当y = y i+1时，x a b y c x b ai i i i ++=-⋅-=-111(); 其中∆x b a=- 为常数， · 算法过程polyfill (polygon, color)int color;多边形定义 polygondef ;{ for (各条扫描线i ){ 初始化新边表头指针NET [i]；把y min = i 的边放进边表NET [i]; }y = 最低扫描线号；初始化活性边表AET 为空；for (各条扫描线i ){ 把新边表NET [i] 中的边结点用插入排序法插入AET表，使之按x坐标递增顺序排列；遍历AET表，把配对交点区间(左闭右开)上的象素(x, y)，用drawpixel (x, y, color) 改写象素颜色值；遍历AET表，把y max= i 的结点从AET表中删除，并把y max > i 结点的x值递增 x；若允许多边形的边自相交，则用冒泡排序法对AET表重新排序；}} /* polyfill */⑤问题及其求解问题1：扫描线与多边形顶点相交，交点的取舍。

• 1、扫描线填充 • 算法基本过程：给定种子点，首先填充种子 点所在扫描线上给定的一个区段，然后确定与这 一区段相连通的上、下两条扫描线上位于该区段 内是否存在需要填充的新区段，如果存在，就填 充并依次保存下来。反复这个过程，直到填充结 束。
• 2、种子填充算法又称为边界填充算法 • P396
•
在压栈的过程中，每有一个数据压入堆 栈，就放在和前一个单元相连的后面一个 单元中，堆栈指示器中的地址自动加1。读 取这些数据时，按照堆栈指示器中的地址 读取数据，堆栈指示器中的地址数自动减 1。 这个过程叫做“弹出pop”。如此就实现了 后进先出的原则。
• 漫水法：是对内定义区域进行填充的算法， 它的基本方法：首先在区域内测试一点(x,y) 的象素值，看其是否具有原始给定的值， 也即决定该点是否在区域内且未被填充过， 如果是，则改变其颜色或亮度，然后再在 其四个或八个方向上扩展，继续测试，通 过递归调用，实现四连通式或八连通式的 区域填充。
堆栈(Stack)的几点介绍： 1、堆栈都是一种数据项按序排列的数据 结构，只能在一端(称为栈顶(top))对数据项进 行插入和删除。要点：堆：顺序随意；栈：后 进先出(Last-In/First-Out)。堆和栈是两个不同 的概念。堆（heap）上分配的内存，系统不 释放，而且是动态分配的。栈（stack）上分 配的内存系统会自动释放，它是静态分配的。 运行时栈叫堆栈。栈的分配是从内存的高地址 域的过程中不关心区 域的形状，而是通过获得区域内部的任何一个像 素，并以这个像素为种子，不断扩大填充的面积， 最终覆盖整个填充区域。这个算法的关键是连通 像素的搜索和边界的判断。
• (1)连通像素的搜索：P397 • (2)边界的判断：P398
• 堆栈

7
9 9
9
对边界和内点表示的八连通区域的填充，只要将上述算法的对四 个像素点填充改为八个像素点即可。 四连通区域种子填充算法的缺点是有时不能通过狭窄区域区域， 因而不能填满多边形。八连通算法的缺点是有时会填出多边形的 边界。由于填不满比涂出更容易补救，因此四连通算法比八连通 算法用得更多。
（3）扫描线种子填充算法
（2）内点表示的四连通区域种子填充算法
基本思想：从多边形内部任一点（像素）出发，按照“右 上左下”的顺序判断相邻像素，若是区域内的像素，则对 其填充，并重复上述过程，直至所有像素填充完毕。 可以使用栈结构来实现该算法，种子像素入栈，档栈非空， 重复执行下面操作： 1）栈顶像素出栈； 2）将出栈像素置成多边形填充的颜色；
基本思想：从多边形内部任一点（像素）出发，按照 “右上左下”的顺序判断相邻像素，若不是边界像素 且没被填充过，则对其填充，并重复上述过程，直至 所有像素填充完毕。 可以使用栈结构来实现该算法，种子像素入栈，档栈 非空，重复执行下面操作： 1）栈顶像素出栈； 2）将出栈像素置成多边形填充的颜色； 3）按“右上左下”的顺序检查与出栈像素相邻的四个 像素，若其中某个像素不在边界上且未置成多边形色， 则把该像素入栈。
扫描线算法分析（举例分析）
基本思想：在任意不间断的区间中只取一个像素（不 间断区间指一条扫描线上的一组相邻元素），填充当 前扫描线上的该段区间，然后确定与这一段相邻的上 下两条扫描线位于区域内的区段，并依次把它们保存 起来，反复进行这个过程，指导所有保存的每个区段 都填充完毕。
（3）扫描线种子填充算法
种子像素入栈,当栈非空时，重复以下步骤： (1)栈顶像素出栈 (2)沿扫描线对出栈像素的左右像素进行填充， 直到遇到边界像素为止 (3)将上述区间内最左、最右像素记为xl 和xr (4)在区间[xl ,xr]中检查与当前扫描线相邻的上 下两条扫描线是否全为边界像素、或已填充 的像素，若为非边界、未填充的像素，则把 每一区间的最右像素取为种子像素入栈

实验二4-10一、实验题目扫描线种子填充算法是通过扫描线来填充多边形内的水平像素段，处理每条扫描线时仅需将其最右端像素入栈，可以有效提高填充效率。

请使用MFC编程填充图4-60所示的空心体汉字（四连通），填充效果如图4-61所示。

二、实验思想扫描线种子填充算法：先将种子像素入栈，种子像素为栈底像素，如果栈不为空，执行如下4步操作。

（1）栈顶像素出栈。

（2）沿扫描线对出栈像素的左右像素进行填充，直至遇到边界像素为止。

即每出栈一个像素，就对区域内包含该像素的整个连续区间进行填充。

（3）同时记录该区间，将区间最左端像素记为x left，最右端像素记为x right。

（4）在区间〔x left，x right〕中检查与当前扫描线相邻的上下两条扫描线的有关像素是否全为边界像素或已填充像素，若存在非边界且未填充的像素，则把未填充区间的最右端像素取作种子像素入栈。

三、实验代码void CTestView::OnLButtonDown(UINT nFlags, CPoint point)//左键按下函数{// TODO: Add your message handler code here and/or call defaultSeed=point;//选择种子位置CharFill();//进行填充CView::OnLButtonDown(nFlags, point);}void CTestView::CharFill()//文字填充函数{CRect Rect;GetClientRect(&Rect);CClientDC dc(this);COLORREF BoundColor;//边界色int Width=Rect.right-Rect.left;int Hight=Rect.bottom-Rect.top ;int Flag;int x0,y0,x,y;CPoint Point;std::vector<CPoint> FillBuffle;//定义CPoint类型的数组序列对象FillBuffle.reserve(10);//定义数组序列的大小FillBuffle.push_back(CPoint(Seed)); //把种子结点压入数组序列BoundColor=RGB(0,0,0);//定义边界色为黑色while(!FillBuffle.empty())//如果数组序列非空{Point=FillBuffle.front();//弹出数组序列头元素x=Point.x;y=Point.y;FillBuffle.erase(FillBuffle.begin());//清除数组序列内的元素dc.SetPixel(Point,Fillcolor);//绘制像素//判断像素的位置是否在图形内部x0=x+1;//右方判断while(dc.GetPixel(x0,y)!=BoundColor&&dc.GetPixel(x0,y)!=Fillcolor) {x0=x0+1;if(x0>=Width)//到达屏幕最右端{MessageBox("种子超出范围","警告");RedrawWindow();return;}}y0=y+1;//下方判断while(dc.GetPixel(x,y0)!=BoundColor&&dc.GetPixel(x,y0)!=Fillcolor) {y0=y0+1;if(y0>=Hight)//到达屏幕最下端{MessageBox("种子超出范围","警告");RedrawWindow();return;}}RightPoint.x=x0;//右边界内的左邻点x0=x-1;while(dc.GetPixel(x0,y)!=Fillcolor&&dc.GetPixel(x0,y)!=BoundColor){dc.SetPixel(x0,y,Fillcolor);x0=x0-1;if(x0<=0)//到达屏幕最左端{MessageBox("种子超出范围","警告");RedrawWindow();return;}}y0=y-1;while(dc.GetPixel(x,y0)!=BoundColor&&dc.GetPixel(x,y0)!=Fillcolor){y0=y0-1;if(y0<=0)//到达屏幕最上端{MessageBox("种子超出范围","警告");RedrawWindow();return;}}LeftPoint.x=x0+1;//左边界内的右邻点x0=LeftPoint.x;y=y+1;//下一条扫描线while(x0<RightPoint.x){Flag=0;while((dc.GetPixel(x0,y)!=Fillcolor)&&(dc.GetPixel(x0,y)!=BoundColor)) {if(Flag==0)Flag=1;x0++ ;}if(Flag==1){if((x0==RightPoint.x)&&(dc.GetPixel(x0,y)!=Fillcolor)&&(dc.GetPixel(x0,y)!=BoundColor))FillBuffle.push_back(CPoint(x0,y));//进入数组序列else{FillBuffle.push_back(CPoint(x0-1,y));}Flag=0;}PointNext.x=x0;while(((dc.GetPixel(x0,y)==Fillcolor)&&(x0<RightPoint.x))||((dc.GetPixel(x0,y)==BoundColor) &&(x0<RightPoint.x))){x0 ++;}}x0=LeftPoint.x;y=y-2;while(x0<RightPoint.x){Flag=0;while((dc.GetPixel(x0,y)!=Fillcolor)&&(dc.GetPixel(x0,y)!=BoundColor)&&(x0<RightPoint.x)) {if(Flag==0)Flag=1;x0++ ;}if(Flag==1){if((x0==RightPoint.x)&&(dc.GetPixel(x0,y)!=Fillcolor)&&(dc.GetPixel(x0,y)!=BoundColor))FillBuffle.push_back(CPoint(x0,y));else{FillBuffle.push_back(CPoint(x0-1,y));}Flag=0;}PointNext.x=x0;while((dc.GetPixel(x0,y)==Fillcolor&&x0<RightPoint.x)||(dc.GetPixel(x0,y)==BoundColor&&x 0<RightPoint.x)){x0++;}}}FillBuffle.clear();return;}void CTestView::OnMENUFill(){// TODO: Add your command handler code hereRedrawWindow();MessageBox("请在空心字体内部单击鼠标左键!","提示");}四、实验结果截图。

计算机图形学——区域填充的扫描线算法一．实验名称：区域填充的扫描线算法二．实验目的：1、理解区域填充扫描线算法的原理；2、实现区域填充的扫描线算法并测试；三．算法原理：算法基本思想: 首先填充种子点所在扫描线上位于区域内的区段，然后确定与该区段相邻的上下两条扫描线上位于区域内的区段，并依次将各区段的起始位置保存, 这些区段分别被用区域边界色显示的像素点所包围。

随后,逐步取出一开始点并重复上述过程，直到所保存各区段都填充完毕为止。

借助于栈结构，区域填充的扫描线算法之步骤如下：Step 1. 初始化种子点栈：置种子点栈为空栈，并将给定的种子点入栈；Step 2. 出栈：若种子点栈为空，算法结束；否则，取栈顶元素(x，y)为种子点；Step 3. 区段填充：从种子点(x, y) 开始沿纵坐标为y 的当前扫描线向左右两个方向逐像素点进行填色，其颜色值置为newcolor 直至到达区域边界。

分别以xl 和xr 表示该填充区段两端点的横坐标；Step 4. 新种子点入栈: 分别确定当前扫描线上、下相邻的两条扫描线上位于区段[xl, xr] 内的区域内的区段。

若这些区段内的像素点颜色值为newolor ,则转至Step 2；否则以区段的右端点为种子点入种子点栈，再转至Step 2。

四．原程序代码：/*****************************************//*4-ScanLineFill 区域填充的扫描线算法实现*//*****************************************/#include <stdio.h>#include <conio.h>#include <graphics.h>#include <malloc.h>#define Stack_Size 100 //栈的大小常量//定义结构体,记录种子点typedef struct{int x;int y;}Seed;//定义顺序栈(种子点)typedef struct{Seed Point[Stack_Size];int top;}SeqStack;//初始化栈操作void InitStack(SeqStack *&S){S=(SeqStack *)malloc(sizeof(SeqStack));S->top=-1;}//种子点栈置空；void setstackempty (SeqStack *S){S->top==-1;}//种子点栈状态检测函数int isstackempty (SeqStack *S){if(S->top==-1)return true; //空栈返回trueelsereturn false; //非空栈返回false}//种子点入栈；int stackpush (SeqStack *&S,Seed point){if(S->top==Stack_Size-1)//栈已满，返回false return false;S->top++;//栈未满，栈顶元素加1S->Point[S->top]= point;return true;}//取栈顶元素；int stackpop (SeqStack *&S,Seed &point){if(S->top==-1)//栈为空，返回falsereturn false;point=S->Point[S->top];S->top --;//栈未空，top减1return true;}//画圆void CirclePoints (int xc, int yc, int x, int y, int Color) {putpixel (xc + x, yc + y, Color);putpixel (xc + x, yc - y, Color);putpixel (xc - x, yc + y, Color);putpixel (xc - x, yc - y, Color);putpixel (xc + y, yc + x, Color);putpixel (xc + y, yc - x, Color);putpixel (xc - y, yc + x, Color);putpixel (xc - y, yc - x, Color); }//中点画圆算法void MidpointCircle(int radius, int Color) {int x, y;float d;x=0;y=radius;d=5.0/4-radius;CirclePoints(250,250,x,y,Color);while(x<y){if (d<0){d+=x*2.0+3;}else{d+=(x-y)*2.0+5;y--;}x++;CirclePoints(250,250,x,y,Color);}}//四连通扫描线算法void ScanLineFill4(int x, int y, int oldcolor, int newcolor) {int xl, xr, i;bool SpanNeedFill;Seed pt;//种子点SeqStack *S;//定义顺序栈InitStack(S);//定义了栈之后必须把栈先初始化setstackempty(S);//种子点栈置空；pt.x = x;pt.y = y;stackpush (S,pt); // 种子点(x, y)入栈while (!isstackempty(S)){stackpop (S,pt);//取种子点y = pt.y;x = pt.x;while (getpixel (x,y)==oldcolor) {// 从种子点开始向右填充putpixel (x, y, newcolor);x++;}xr = x -1;x = pt.x -1;while (getpixel (x,y)==oldcolor) { // 从种子点开始向左填充putpixel (x, y, newcolor);x--;}xl = x + 1;x = xl;y = y +1; // 处理上面一条扫描线while (x < xr){SpanNeedFill = false;while (getpixel (x, y)==oldcolor){SpanNeedFill = true;x++ ;} // 待填充区段搜索完毕if (SpanNeedFill){// 将右端点作为种子点入栈pt.x = x - 1;pt.y = y;stackpush (S,pt);SpanNeedFill = false;} //继续向右检查以防遗漏while ((getpixel (x, y)!=oldcolor) && (x< xr)) x++;} //上一条扫描线上检查完毕x = xl;y=y-2; // 处理下面一条扫描线while (x < xr){SpanNeedFill = false;while (getpixel (x, y)==oldcolor){SpanNeedFill=true;x++ ;}if (SpanNeedFill){pt.x= x - 1;pt.y = y;stackpush (S,pt);SpanNeedFill=false;}while ((getpixel (x, y)!=oldcolor) && (x < xr))x++;}}}//主函数检测void main(){int radius,color;int x,y;//种子点int oldcolor,newcolor;//原色与填充色//输入参数值printf("input radius and color:\n");//画圆参数scanf("%d,%d",&radius,&color);printf("input x and y:\n"); //读入内点scanf("%d,%d", &x, &y);printf("input oldcolor and newcolor:\n"); //读入原色与填充色scanf("%d,%d", &oldcolor, &newcolor);int gdriver = DETECT,gmode;initgraph(&gdriver, &gmode, "c:\\tc");// 用背景色清空屏幕cleardevice();// 设置绘图色为红色setcolor(RED);MidpointCircle(radius,color);//用中点画圆算法画圆rectangle(150, 150, 350, 350);//再画一个矩形区域ScanLineFill4 (x,y,oldcolor,newcolor);//扫描线区域填充getch();closegraph();}五．运行结果与讨论：测试结果1：测试结果2：六．实验分析与讨论：1.通过借助栈这一数据结构，完成了区域填充的扫描线算法的实现，并利用以前所学的画圆等算法，进行综合运用，在此基础上进行扩充，设计多种图案，进行扫描线填充算法的检测，都得到了理想的结果，体现了算法的有效性；2.栈的数据结构给种子点的操作带来了极大的方便，为算法的实现提供了便利，同时还提高了算法的复用性和可靠性；3.此扫描线填充算法能够对多种图案进行填充，展现了算法的实用性。

该算法具有运算速度快、对图形的适应性强、 填充结果重复性好等优点；它从根本上克服了多 边形填充法对区域形状有一定限制，种子填充法 要求知道区域内一点（填充胚）以及对区域内像 素点进行重复判断等弊端；而且该算法适应于任 何一种可以准确描绘出边界曲线的区域填充处理。
3、基于曲线积分的区域填充算法
• 算法的实现： ➢对一个区域进行轮廓跟踪，求出区域的边
• 改进算法的基本思想是：每找到一个新的内部
区段时,不仅将新区段的y值(yn)和左右列值xnl， xnr压入堆栈，而且同时把当前区段的y值和左右 列值xl,xr也压入堆栈，以保存和传递有关的信息。
3、基于曲线积分的区域填充算法
基于曲线积分的区域填充算法是邓国强，孙 景鳌等（2001）提出的一种以格林公式求区域面 积为基本原理进行区域填充的特殊算法。
1、递归种子填充算法
递归种子填充算法，又称边界填色算 法。
算法的原理是：让单个像元作为填充 胚，在给定的区域范围内，通过某种方法 进行蔓延，最终填充满整个多边形区域。 为了实现填充胚的蔓延，可采用四邻法或 八邻法进行填充。
2、扫描线种子填充算法
（1）扫描线种子填充算法
扫描线种子填充算法的对象是一个个扫描 线段。扫描线段是指区域内同值相邻像素 在水平方向的组合，它的两端以具有边界 值的像素为边界，即一段扫描线段的中间 只有同一种像素。
（2）计算多边形面积
4、区域填充算法在地图制图中的应用
（2）计算多边形面积
Sa
24
1 5 2
1 13 33 2
Sb
30
1 2
5
1 2
17
41
ScΒιβλιοθήκη 1031 213
1 2
17

在扫描线段的填充 ， 并记 下该 线段 左 右 边界 。再 在 这 个边 界 确 定 的 Ｘ范 围 内 ， 在 已填 充的 扫 描 线段 相 邻 的 上 、 下 扫 描 线 中搜 寻 新 的 种子 ， 若有 新 种 子 则 对 其 所 在 扫描 线段 填 充 。 这 种 搜 寻 种 子 的 方 式 能 确 保各 个相 邻 支路 都 被 搜 索到 。 通过“ 递推” 和“ 回推” 能 实现 复
区 间 。这 种 填 充 算 法 需 要 解 决 交 点 取 舍 和边 界 象 素 取 舍 问题 ， 对 于 非 直 线 围 成 的 边 界 用 这 种 填 充 算 法 处 理 起 来 十分 困难 ， 而 对 直 线 围 成 的 边 界 虽 然 可 采 用 活 性 边 表 来 提 高处 理 效 率 。 但 对 各种表的维护和排序使存储空间开销太大 ； 边 缘 填 充 的 基 本 思
方 向搜 索 下 一 象 素 ， 这将把太多的象素压人堆栈 ， 故效率不高 ， 存 储 空 间 开 销 还是 太 大 。 改 进 的种 子 填 充 法 称 扫 描线 种 子 填 充
发， 循环 读取右邻点 颜色码 ， 每 读 取 一 个 右 邻 点 颜 色 码 都 与 边
界 色 码 比较 ， 若 不 同就 将 该 点 刷 新 为 填充 色 。当 读 到 边界 色码 ，
ｖ ０ ． ５ Ｎ ｏ ． １
娌斜铷 右
教 育 教 学１
扫描 线种 子填 充算法 的解析
申小颂
（ 成 都 信 息 工 程 学 院 控 制 工 程 学 院 四川 成 都 摘 ６ １ ０ ２ ２ ５ ） 要： 扫 描 线 种子 填 充 算 法 效 率 较 高 、 占用存 储 空 间较 少。 编程时 ， 可 由初 始种 子 出发 ， 分 别 向 左右 两个 方 向 循 环 读 点 实 现种 子所

{push(x–1,y);右端点进栈
span-need–fill:=false;} while(getpixel(FB,x,y)=B-color or getpixel(FB,x,y)=N-color)and x<xright do {x:=x+1} } ; *在上一条扫描上检查完* y:=y–2; *在扫描线y–1上从左向右地检查位于区间 [xletft, xright]上的象素，其方法与在扫描线
算法
while stack–not–empty do {pop(x,y)；*从堆栈中取一种子象素* savex:=x: *保存横坐标x的值* while getpixel (FB, x, y), <> B–color do {setpixel (FB, x, y, N–color); x:=x+1} xright:=x–1 *保存线段的右端点* while getpixel (FB,x,y)<>N–color and getpixel (FB,x,y), <> B–color do {span–need–fill:=true; x:=x+1;} if span–need–fill then
x:=savex–1; {*向种子的左边填充*}
while getpixel (FB, x, y) <> B–color do { setpixel (FB, x, y, N–color); x:=x–1}
xleft:=x+1 *保存线段的左端点*
x:=xleft; y:=y+1; while x<=xright do {span–need–fill:=false;
y+1上检查的情况完全一样，故略去详情*

扫描线填充种子填充算法（原创完整版）// 计算机图形学View.cpp : implementation of the CMyView class//// 种子填充和扫描线填充算法// Author:: codeants_for_sdau2012// Date::2014/10/24#include "stdafx.h"#include "计算机图形学.h"#include "计算机图形学Doc.h"#include "计算机图形学View.h"#include "DDA.h"#include "afxtempl.h"#include#include#include#include "debug1.h"#include "xyz_dialog.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endifusing namespace std;/////////////////////////////////////////////////////////////////// //////////// CMyViewIMPLEMENT_DYNCREATE(CMyView, CView)BEGIN_MESSAGE_MAP(CMyView, CView)//{{AFX_MSG_MAP(CMyView)ON_COMMAND(ID_MENUITEM32771, OnDDA)ON_COMMAND(ID_MENUITEM32772, OnBrem)ON_COMMAND(ID_MENUITEM32773, OnSqureBrush)ON_COMMAND(ID_MENUITEM32774, Onseek1)ON_COMMAND(ID_MENUITEM32775, OnSeekin8)ON_COMMAND(ID_MENUITEM32776, OnAETLine)//}}AFX_MSG_MAP// Standard printing commandsON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, CView::OnFilePrint) ON_COMMAND(ID_FILE_PRINT_PREVIEW,CView::OnFilePrintPreview) END_MESSAGE_MAP()/////////////////////////////////////////////////////////////////// //////////// CMyView construction/destructionCMyView::CMyView(){// TODO: add construction code here}CMyView::~CMyView(){}BOOL CMyView::PreCreateWindow(CREATESTRUCT& cs){// TODO: Modify the Window class or styles here by modifying// the CREATESTRUCT csreturn CView::PreCreateWindow(cs);}/////////////////////////////////////////////////////////////////// //////////// CMyView drawingvoid CMyView::OnDraw(CDC* pDC){CMyDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data here}/////////////////////////////////////////////////////////////////// //////////// CMyView printingBOOL CMyView::OnPreparePrinting(CPrintInfo* pInfo){// default preparationreturn DoPreparePrinting(pInfo);}void CMyView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) {// TODO: add extra initialization before printing}void CMyView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) {// TODO: add cleanup after printing}/////////////////////////////////////////////////////////////////// //////////// CMyView diagnostics#ifdef _DEBUGvoid CMyView::AssertValid() constCView::AssertValid();}void CMyView::Dump(CDumpContext& dc) const{CView::Dump(dc);}CMyDoc* CMyView::GetDocument() // non-debug version is inline{ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CMyDo c)));return (CMyDoc*)m_pDocument;}#endif //_DEBUG/////////////////////////////////////////////////////////////////// //////////// CMyView message handlersvoid swap(int& xt,int& yt){int tmp=xt;xt=yt;yt=tmp;}void DDAxt(int x0,int y0,int x1,int y1,int color,CDC* pDC){int x;float dx,dy,k;dx=x1-x0;dy=y1-y0;if(dx==0)if(y1<y0)< bdsfid="172" p=""></y0)<>swap(y1,y0);for(int y=y0;y<y1;y++)< bdsfid="175" p=""></y1;y++)<> {pDC->SetPixel(x1,y,color);}return;}k=dy/dx; double y=y0;if(x0>x1){swap(x0,x1);swap(y0,y1);}for(x=x0;x<=x1;x++){pDC->SetPixel(x,int (y+0.5), color);y=y+k;}}int x0,y0,x1,y1;void CMyView::OnDDA(){DDA s1;//debug1 d1;s1.DoModal();//Invalidate();//UpdateData(true);x0=s1.m_x0;y0=s1.m_y0;x1=s1.m_x1;y1=s1.m_y1;//UpdateData(false);//s1.EndDialog(3);CDC* pDC;pDC=GetDC();CMyDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);DDAxt(x0,y0,x1,y1,RGB(255,0,255),pDC);}void Brem(int x0,int y0,int x1,int y1,int color,CDC* pDC) { double xt,yt,k,b;double dx,dy,d0,dt1,dt2;if(x0>x1){swap(x0,x1);swap(y0,y1);}dx=x1-x0,dy=y1-y0;if(x1==x0){if(y1<y0)< bdsfid="225" p=""></y0)<>swap(y1,y0);for(int y=y0;y<y1;y++)< bdsfid="228" p=""></y1;y++)<> {pDC->SetPixel(x1,y,color);}return;}k=(y1-y0)/(x1-x0);b=(x1*y0-x0*y1)/(x1-x0);if(k<=1&&k>=0){d0=dx-2*dy;dt1=2*dx-2*dy;dt2=-2*dy;int y=y0;for(int x=x0;x<=x1;x++){if(d0<0){y++;d0+=dt1;}else d0+=dt2;pDC->SetPixel(x,y,color);}}else if(k>1){if(y1<y0)< bdsfid="256" p=""></y0)<> {swap(x1,x0);swap(y1,y0);dx=-dx;dy=-dy;}d0=dx-2*dy;dt1=2*dy-2*dx;dt2=-2*dx;int x=x0;for(int y=y0;y<=y1;y++){if(d0<0){x++;d0+=dt1;}else d0+=dt2;pDC->SetPixel(x,y,color);}}else if(k<0&&k>=-1){if(x1<x0)< bdsfid="281" p=""></x0)<> {swap(x1,x0);swap(y1,y0);dx=-dx;dy=-dy;}d0=-dx;dt1=-2*dx-2*dy;dt2=-2*dy;int y=y0;for(int x=x0;x<=x1;x++){if(d0>=0){y--;d0+=dt1;}else d0+=dt2;pDC->SetPixel(x,y,color);}}else if(k<-1){if(y1<y0)< bdsfid="306" p=""></y0)<> {swap(x1,x0);swap(y1,y0);dx=-dx;dy=-dy;}d0=-dy;dt1=-2*dy-2*dx;dt2=-2*dx;int x=x0;for(int y=y0;y<=y1;x++){if(d0>=0){x--;d0+=dt1;}else d0+=dt2;pDC->SetPixel(x,y,color);}}}void CMyView::OnBrem(){DDA s1;//debug1 d1;s1.DoModal();//Invalidate();//UpdateData(true);x0=s1.m_x0;y0=s1.m_y0;x1=s1.m_x1;y1=s1.m_y1;//UpdateData(false);//s1.EndDialog(3);CDC* pDC;pDC=GetDC();CMyDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);Brem(x0,y0,x1,y1,RGB(255,0,255),pDC);}void squr(int x0,int y0,int x1,int y1,int color,CDC* pDC) { pDC->SetPixel(x0,y0,color);pDC->SetPixel(x0+1,y0,color);pDC->SetPixel(x0+1,y0+1,color);pDC->SetPixel(x0+1,y0-1,color);pDC->SetPixel(x0,y0+1,color);pDC->SetPixel(x0,y0-1,color);pDC->SetPixel(x0-1,y0,color);pDC->SetPixel(x0-1,y0+1,color);pDC->SetPixel(x0-1,y0-1,color);pDC->SetPixel(x1,y1,color);pDC->SetPixel(x1+1,y1,color);pDC->SetPixel(x1+1,y1+1,color);pDC->SetPixel(x1+1,y1-1,color);pDC->SetPixel(x1,y1+1,color);pDC->SetPixel(x1,y1-1,color);pDC->SetPixel(x1-1,y1,color);pDC->SetPixel(x1-1,y1+1,color);pDC->SetPixel(x1-1,y1-1,color);}void CMyView::OnSqureBrush(){DDA s1;s1.DoModal();//Invalidate();//UpdateData(true);x0=s1.m_x0;y0=s1.m_y0;x1=s1.m_x1;y1=s1.m_y1;//UpdateData(false);//s1.EndDialog(3);CDC* pDC;pDC=GetDC();CMyDoc* pDoc = GetDocument(); ASSERT_V ALID(pDoc);Brem(x0,y0,x1,y1,RGB(255,0,255),pDC); Brem(x0,y0,101,1001,RGB(255,0,255),pDC); //squr(x0,y0,x1,y1,RGB(255,0,255),pDC);}void seekIn(int x,int y,int color,CDC* pDC)//4方向的填充{ CArray my1;//CArray *first,*rear;my1.Add(CPoint(x,y));pDC->SetPixel(x,y,color);//first=&my1.ElementAt(0);//int first=0,rear=1;while(my1.GetSize()!=0){CPoint p=my1.GetAt(0);my1.RemoveAt(0);CPoint tmp=CPoint(p.x+1,p.y);if(pDC->GetPixel(tmp)!=color){pDC->SetPixel(p.x+1,p.y,color);my1.Add(tmp);}tmp=CPoint(p.x-1,p.y);if(pDC->GetPixel(tmp)!=color){pDC->SetPixel(p.x-1,p.y,color);my1.Add(tmp);}tmp=CPoint(p.x,p.y+1);if(pDC->GetPixel(tmp)!=color){pDC->SetPixel(p.x,p.y+1,color);my1.Add(tmp);}tmp=CPoint(p.x,p.y-1);if(pDC->GetPixel(tmp)!=color){pDC->SetPixel(p.x,p.y-1,color);my1.Add(tmp);}}}void seekIn8(int x,int y,int color,CDC* pDC)//8方向的填充{ CArray my1;//CArray *first,*rear;my1.Add(CPoint(x,y));pDC->SetPixel(x,y,color);//first=&my1.ElementAt(0);//int first=0,rear=1;while(my1.GetSize()!=0){CPoint p=my1.GetAt(0);my1.RemoveAt(0);CPoint tmp=CPoint(p.x+1,p.y);if(pDC->GetPixel(tmp)!=color){pDC->SetPixel(p.x+1,p.y,color);my1.Add(tmp);}tmp=CPoint(p.x-1,p.y);if(pDC->GetPixel(tmp)!=color){pDC->SetPixel(p.x-1,p.y,color);my1.Add(tmp);tmp=CPoint(p.x,p.y+1);if(pDC->GetPixel(tmp)!=color) {pDC->SetPixel(p.x,p.y+1,color); my1.Add(tmp);}tmp=CPoint(p.x,p.y-1);if(pDC->GetPixel(tmp)!=color) {pDC->SetPixel(p.x,p.y-1,color); my1.Add(tmp);}tmp=CPoint(p.x+1,p.y+1);if(pDC->GetPixel(tmp)!=color) {pDC->SetPixel(p.x+1,p.y+1,color); my1.Add(tmp);}tmp=CPoint(p.x-1,p.y+1);if(pDC->GetPixel(tmp)!=color) {pDC->SetPixel(p.x-1,p.y+1,color); my1.Add(tmp);}tmp=CPoint(p.x-1,p.y-1);if(pDC->GetPixel(tmp)!=color) {pDC->SetPixel(p.x-1,p.y-1,color); my1.Add(tmp);tmp=CPoint(p.x+1,p.y-1);if(pDC->GetPixel(tmp)!=color){pDC->SetPixel(p.x+1,p.y-1,color);my1.Add(tmp);}}}void CMyView::Onseek1()//四方向的种子填充算法{ CDC* pDC;pDC=GetDC();CMyDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);CPoint p[4];p[0]=CPoint(20,40);p[1]=CPoint(20,400);p[2]=CPoint(200,400);p[3]=CPoint(200,40);int color=RGB(255,0,255);pDC->MoveTo(p[0]);for(int i=1;i<=3;i++){pDC->LineT o(p[i]);}pDC->LineT o(p[0]);color=pDC->GetPixel(p[1]);seekIn(110,220,color,pDC);}void CMyView::OnSeekin8() //8方向的种子填充算法{CDC* pDC;pDC=GetDC();CMyDoc* pDoc = GetDocument(); ASSERT_V ALID(pDoc);CPoint p[4];p[0]=CPoint(320,40);p[1]=CPoint(320,400);p[2]=CPoint(500,400);p[3]=CPoint(500,40);int color=RGB(255,0,255);pDC->MoveTo(p[0]);for(int i=1;i<=3;i++){pDC->LineT o(p[i]);}pDC->LineT o(p[0]);color=pDC->GetPixel(p[1]);seekIn8(410,220,color,pDC);}//扫描线填充struct edge//edge信息{double xi;double dx;int ymax;bool operator <(edge& S)const{return xi<s.xi;< bdsfid="539" p=""></s.xi;<> }};void initLineNewedge(vector< list >& ve,vector& py,int ymin,int ymax)//初始化边参数{edge e;int sz=py.size();for(int i=0;i<sz;i++)< bdsfid="549" p=""></sz;i++)<>{CPoint& ps=py[i];CPoint& pe=py[(i+1)%sz];CPoint& pee=py[(i+2)%sz];CPoint& pss=py[(i-1+sz)%sz];if(pe.y!=ps.y){e.dx=(double)(pe.x-ps.x)/(double)(pe.y-ps.y);if(pe.y>ps.y){e.xi=ps.x;if(pee.y>=pe.y) e.ymax=pe.y-1;else e.ymax=pe.y;ve[ps.y-ymin].push_front(e);}else{e.xi=pe.x;if(pss.y>=ps.y) e.ymax=ps.y-1;else e.ymax=ps.y;ve[pe.y-ymin].push_front(e);}}}void insertNetListT oAet(list& st,list& aet)//插入活动边{for(list::iterator it=st.begin();it!=st.end();it++)aet.push_front((*it));}void fillScannLine(list& st,int y,int color,CDC* pDC)//填充{CPen pen;pen.CreatePen(PS_SOLID,2,RGB(255,0,255));CPen* pOldPen=pDC->SelectObject(&pen);int sz=st.size();for(list::iterator it=st.begin();it!=st.end();++it){pDC->MoveTo(CPoint((*it).xi,y));++it;pDC->LineT o(CPoint((*it).xi,y));}pDC->SelectObject(pOldPen);}void RemoveNonActiveLine(list& st,int y)//删除非活动边{for(list::iterator it=st.begin();it!=st.end();){if((*it).ymax==y)it=st.erase(it);else it++;}}void UpdateAetEdgeInfo(edge& e)e.xi += e.dx;}void updateAndResortAet(list& st)//更新活动边和对活动边进行排序{for(list::iterator it=st.begin();it!=st.end();it++){(*it).xi+=(*it).dx;}st.sort();}void hzLine(vector& py,CDC* pDC){int sz=py.size();CPen newpen;newpen.CreatePen(PS_SOLID,1,RGB(255,0,255));CPen* pOldPen=pDC->SelectObject(&newpen);for(int i=1;i<sz;i++)< bdsfid="631" p=""></sz;i++)<>{if(py[i].y==py[i-1].y){pDC->MoveTo(CPoint(py[i-1].x,py[i-1].y));pDC->LineT o(CPoint(py[i].x,py[i].y));}}if(py[sz-1].y==py[0].y){pDC->MoveTo(CPoint(py[0].x,py[0].y));pDC->LineT o(CPoint(py[sz-1].x,py[sz-1].y));}pDC->SelectObject(pOldPen);}void CMyView::OnAETLine(){vector py;py.clear();int ymax=-1000001,ymin=1000001;/*xyz_dialog xz[6];for(int i=0;i<6;i++){xz[i].DoModal();UpdateData(true);if(ymaxelse if(ymin>xz[i].m_y) ymin=xz[i].m_y; py.push_back(CPoint(xz[i].m_x,xz[i].m_y)); UpdateData(false);}*/CPoint p[6];p[0]=CPoint(200,40);p[1]=CPoint(200,300);p[2]=CPoint(350,170);p[3]=CPoint(400,170);p[4]=CPoint(500,300);p[5]=CPoint(500,40);ymin=40;ymax=300;for(int i=0;i<6;i++){py.push_back(p[i]);}vector< list > ve(ymax-ymin+1);CDC* pDC;pDC=GetDC();CMyDoc* pDoc = GetDocument(); ASSERT_V ALID(pDoc); initLineNewedge(ve,py,ymin,ymax); hzLine(py,pDC);list aet;int color=RGB(255,0,255);//AfxMessageBox("hello world!"); for(int y=ymin;y<=ymax;y++) {insertNetListToAet(ve[y-ymin],aet); fillScannLine(aet,y,color,pDC); RemoveNonActiveLine(aet,y); updateAndResortAet(aet);}}。

二、扫描线种子填充算法实现
借助于堆栈，上述算法实现步骤如下：
1、初始化堆栈。 2、种子压入堆栈。 3、while（堆栈非空） { (1)从堆栈弹出种子象素。 (2)如果种子象素尚未填充，则：
a.求出种子区段：xleft、xright; b.填充整个区段。 c.检查相邻的上扫描线的xleft≤x≤xright区间内， 是否存在需要填充的新区段，如果存在的话， 则把每个新区段在xleft≤x≤xright范围内的最 右边的象素，作为新的种子象素依次压入堆栈。 d.检查相邻的下扫描线的xleft≤x≤xright区间内， 是否存在需要填充的新区段，如果存在的话， 则把每个新区段在 xleft≤x≤xright范围内的 最右边的象素，作为新的种子象素依次压入堆 栈。 }
扫描线种子填充算法步骤 (1)种子象素入栈。 (2)栈非空时象素出栈，否则结束。 (3)对出栈象素及左、右两边象素填充，直到遇边界XL、XR。 (4)在(XL ，XR) 内查相临的上、下两条扫描线是否为边界或已填充, 如不是，则将每区间的最右边的象素入栈。回到(2)。
练习： 用扫描线种子填充算法，写出图中顺序进栈的种子坐标及 所需最大栈空间
2、国标码 我国除了采用ASCII码外，还制定了汉字编 码的国家标准字符集:中华人民共和国国家标准 信息交换编码，代号为“GB2312－80”。该字符 集共收录常用汉字6763个，图形符号682个。 它规定所有汉字和图形符号组成一个94×94 的矩阵，在此方阵中，每一行称为“区”，用区 码来标识；每一列称为“位”，用位码来标识， 一个符号由一个区码和一个位码共同标识。 区码和位码分别需要7个二进制位，同样， 为了方便，各采用一个字节表示。所以在计算机 中，汉字（符号）国标码占用两个字节。

区域填充算法区域填充算法
下面将介绍两种常见的区域填充算法：扫描线填充算法和种子填充算法。

1. 扫描线填充算法（Scanline Fill Algorithm）：
-扫描线填充算法基于扫描线的原理，从图像的上方向下扫描，对每条扫描线上的像素进行填充。

-算法流程如下：
-选择一个初始扫描线，例如选择图像的最上面一条扫描线；
-遍历该扫描线上的每一个像素，判断是否需要填充该像素；
-如果需要填充，则向区域内部延伸扫描线，同时判断该扫描线上的相邻像素是否需要填充；
-一直延伸扫描线，直到整个区域被填充完毕。

-扫描线填充算法的优点是简单、易于实现，但是算法的效率较低，在处理大尺寸区域时耗时较长。

2. 种子填充算法（Seed Fill Algorithm）：
-种子填充算法基于种子点的概念，选择一个起始点作为种子点，然后根据预设的填充规则进行填充。

-算法流程如下：
-选择一个起始点作为种子点，将该点填充上颜色；
-判断该种子点的相邻像素是否需要填充，如果需要则将其填充；
-一直延伸填充，直到整个区域被填充完毕。

-种子填充算法的优点是效率较高，能够处理较大的区域，但是需要选择合适的填充规则，否则可能会导致填充区域不准确或者出现漏填的情况。

以上两种区域填充算法在实际应用中会根据具体的场景和需求选择合适的算法进行使用。

在实际实现时，还需要考虑一些特殊情况，如图像边界处理、扫描顺序等，以确保算法的正确性和效率。

任意多边形区域的快速填充算法一、前言任意多边形区域的快速填充算法是计算机图形学中的一个重要问题，其应用广泛，例如在计算机游戏、数字地图等领域中都有广泛的应用。

本文将介绍几种常见的任意多边形区域的快速填充算法，包括扫描线算法、边界填充算法、种子填充算法等。

二、扫描线算法扫描线算法是一种基于扫描线原理的填充算法，其基本思想是将区域划分为若干个水平方向上的扫描线，然后在每条扫描线上找到交点，并根据交点进行填充。

具体步骤如下：1. 将多边形顶点按照纵坐标从小到大排序；2. 从最小纵坐标开始，依次向上扫描每条水平方向上的线段；3. 对于每条水平方向上的线段，找到与之相交的多边形边界，并记录下所有交点；4. 根据相邻两个交点之间是否为奇数个来确定是否需要进行填充。

三、边界填充算法边界填充算法也是一种常见的任意多边形区域的快速填充算法，其基本思想是通过递归调用来进行填充。

具体步骤如下：1. 对于每个多边形边界上的像素点，将其标记为“边界点”；2. 从任意一个未填充的内部像素点开始，向四周搜索，如果遇到“边界点”则停止搜索，并将搜索路径上的所有像素点标记为已填充；3. 重复步骤2直到所有内部像素点都被填充。

四、种子填充算法种子填充算法也是一种常见的任意多边形区域的快速填充算法，其基本思想是通过找到一个内部像素点作为“种子”，然后向四周扩散进行填充。

具体步骤如下：1. 随机选择一个内部像素点作为“种子”，并将其标记为已填充；2. 向四周搜索，如果遇到未被标记为已填充的像素，则将其标记为已填充，并加入到待处理列表中；3. 重复步骤2直到待处理列表为空。

五、总结以上介绍了几种常见的任意多边形区域的快速填充算法，每种算法都有其特定的优缺点，选择合适的算法需要根据具体的应用场景进行考虑。

在实际应用中，还需要考虑算法的效率、稳定性、可扩展性等方面的问题。