matlab 酵母培养物的离散阻滞增长模型

matlab 杂质扩散系数程序在MATLAB中，可以使用Fick's second law来模拟杂质的扩散过程。

以下是一个简单的MATLAB程序，用于计算杂质在一维空间中的扩散系数。

matlab.% 定义参数。

D = 1; % 扩散系数。

L = 10; % 空间长度。

t = 5; % 时间。

N = 100; % 离散点数量。

dx = L/N; % 离散步长。

dt = 0.01; % 时间步长。

% 初始化浓度分布。

C = zeros(N,1);C(1) = 1; % 初始浓度。

C_new = zeros(N,1);% 进行扩散计算。

for k = 1:t/dt.for i = 2:N-1。

C_new(i) = C(i) + Ddt/dx^2(C(i+1)-2C(i)+C(i-1)); end.C = C_new;end.% 可视化结果。

x = 0:dx:L-dx;plot(x,C);xlabel('Position');ylabel('Concentration');title('Diffusion of Impurity');这个简单的程序通过离散化空间和时间来模拟杂质的扩散过程。

程序首先定义了扩散系数D、空间长度L、时间t、离散点数量N等参数。

然后初始化了浓度分布，并通过Fick's second law进行迭代计算，最后通过MATLAB的绘图函数可视化了扩散过程的结果。

当然，实际的杂质扩散模拟可能涉及到更复杂的情况，比如多维空间、非均匀材料等，这时候需要更复杂的模型和算法来进行模拟。

希望这个简单的程序能够帮助你入门MATLAB中的杂质扩散模拟。

1. 引言遗传算法是一种模拟自然选择与遗传机制的优化算法，被广泛应用于离散变量优化问题的求解。

在Matlab软件中，有专门的工具箱可以支持遗传算法的实现与应用，极大地方便了工程技术人员进行离散变量优化问题的研究与应用。

本文将介绍Matlab遗传算法工具箱在离散变量优化算例中的应用，并通过具体案例来展示其实际求解效果。

2. Matlab遗传算法工具箱介绍Matlab遗传算法工具箱是Matlab软件的一个重要工具箱，它提供了丰富的遗传算法函数和工具，方便用户进行遗传算法的实现和应用。

在离散变量优化问题的求解中，用户可以利用工具箱提供的函数对问题进行建模、参数设置、运行算法等操作，从而快速高效地求解问题。

3. 离散变量优化算例为了更好地展示Matlab遗传算法工具箱在离散变量优化中的应用效果，我们选取了一个经典的离散变量优化问题作为算例，具体问题描述如下：设有一组零件需要进行装配，零件的形状和尺寸有多种选择。

每种零件的装配工艺和成本不同，需要选择最佳的零件组合方案来满足装配要求并使总成本最低。

假设可供选择的零件种类有n种，每种零件有m个备选方案，且装配每种零件的成本已知。

问应选择哪些零件及其具体方案才能使得总装配成本最低？4. Matlab遗传算法工具箱的应用为了利用Matlab遗传算法工具箱求解上述离散变量优化问题，我们可以按照以下步骤进行操作：1) 利用Matlab的数据处理工具，将零件的备选方案数据以矩阵的形式导入Matlab环境；2) 利用工具箱提供的函数对遗传算法的参数进行设置，例如选择交叉方式、变异方式、群体大小、迭代次数等；3) 利用工具箱提供的函数对离散变量优化问题进行编码和解码，以便算法能够对离散变量进行操作；4) 利用工具箱提供的函数编写适应度函数，用于评价每个个体的适应度；5) 利用工具箱提供的主函数运行遗传算法，获取最优解及其对应的总装配成本。

5. 案例求解结果分析通过上述步骤，我们在Matlab环境中成功应用遗传算法工具箱求解了离散变量优化问题。

习 题 11. 请编写绘制以下图形的MA TLAB 命令，并展示绘得的图形.(1) 221x y +=、224x y +=分别是椭圆2241x y +=的内切圆和外切圆. (2) 指数函数x y e =和对数函数ln y x =的图像关于直线y=x 对称. (3) 黎曼函数1, (0)(0,1)0 , (0,1), 0,1q x p q q x y x x x =>∈⎧=⎨∈=⎩当为既约分数且当为无理数且或者 的图像（要求分母q 的最大值由键盘输入）.3. 两个人玩双骰子游戏，一个人掷骰子，另一个人打赌掷骰子者不能掷出所需点数，输赢的规则如下：如果第一次掷出3或11点，打赌者赢；如果第一次掷出2、7或12点，打赌者输；如果第一次掷出4、5、6、8、9或10点，记住这个点数，继续掷骰子，如果不能在掷出7点之前再次掷出该点数，则打赌者赢. 请模拟双骰子游戏，要求写出算法和程序，估计打赌者赢的概率. 你能从理论上计算出打赌者赢的精确概率吗？请问随着试验次数的增加，这些概率收敛吗？4. 根据表1.14的数据，完成下列数据拟合问题：(1) 如果用指数增长模型0()0()e r t t x t x -=模拟美国人口从1790年至2000年的变化过程，请用MATLAB统计工具箱的函数nlinfit 计算指数增长模型的以下三个数据拟合问题：(i) 取定0x =3.9，0t =1790，拟合待定参数r ；(ii) 取定0t =1790，拟合待定参数0x 和r ； (iii) 拟合待定参数0t 、0x 和r .要求写出程序，给出拟合参数和误差平方和的计算结果，并展示误差平方和最小的拟合效果图.(2) 通过变量替换，可以将属于非线性模型的指数增长模型转化成线性模型，并用MA TLAB 函数polyfit 进行计算，请说明转化成线性模型的详细过程，然后写出程序，给出拟合参数和误差平方和的计算结果，并展示拟合效果图.(3) 请分析指数增长模型非线性拟合和线性化拟合的结果有何区别？原因是什么？(4) 如果用阻滞增长模型00()00()()er t t N x x t x N x --=+-模拟美国人口从1790年至2000年的变化过程，请用MA TLAB 统计工具箱的函数nlinfit 计算阻滞增长模型的以下三个数据拟合问题：(i) 取定0x =3.9，0t =1790，拟合待定参数r 和N ；(ii) 取定0t =1790，拟合待定参数0x 、r 和N ； (iii) 拟合待定参数0t 、0x 、r 和N .要求写出程序，给出拟合参数和误差平方和的计算结果，并展示误差平方和最小的拟合效果图.表1.14 美国人口统计数据(百万人)人口 3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 年份1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2000 人口76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4 281.4习题 21. 继续考虑第2.2节“汽车刹车距离”案例，请问“两秒准则”和“一车长度准则”一样吗？“两秒准则”是否足够安全？对于安全车距，你有没有更好的建议？4. 继续考虑第2.3节“生猪出售时机”案例，假设在第t 天的生猪出售的市场价格（元/公斤）为2()(0)p t p gt ht =-+ (2.4.1) 其中h 为价格的平稳率，取h =0.0002. 其它模型假设和参数取值保持不变.(1) 试比较(2.4.1)式与(2.3.1)式，解释新的假设和原来的假设的区别与联系. (2) 在新的假设下求解最佳出售时机和多赚的纯利润.(3) 做灵敏度分析，分别考虑h 对最佳出售时机和多赚的纯利润的影响. (4) 讨论模型关于价格假设的强健性.5. 继续考虑第2.3节“生猪出售时机”案例，假设在第t 天的生猪体重（公斤）为()000()mtm w w w t w w w e α-=+- (2.4.2) 其中0(0)90w w ==（公斤），270m w =（公斤），其它模型假设和参数取值保持不变.(1) 试比较(2.4.2)式与(2.3.2)式，解释新的假设和原来的假设的区别与联系（提示：说明当α (α>0)取何值时，在t =0时可以保持(0)1w r '==；说明当t 增大时，猪的体重会如何变化）.(2) 在新的假设下求解最佳出售时机和多赚的纯利润.(3) 参数m w 代表猪长成时的最终重量，对m w 做灵敏度分析，分别考虑m w 对最佳出售时机和多赚的纯利润的影响.(4) 讨论模型关于生猪体重假设的强健性.习 题 34. 某成功人士向学院捐献20万元设立优秀本科生奖学金，学院领导打算将这笔捐款以整存整取一年定期的形式存入银行，第二年一到期就支取，取出一部分作为当年的奖学金，剩下的继续以整存整取一年定期的形式存入银行……请你研究这个问题，并向学院领导写一份报告.5. 有一位老人60岁时将养老金10万元以整存零取方式（指本金一次存入，分次支取本金的一种储蓄）存入，从第一个月开始每月支取1000元，银行每月初按月利率0.3%把上月结余额孳生的利息自动存入养老金. 请你计算老人多少岁时将把养老金用完？如果想用到80岁，问60岁时应存入多少钱？10. 继续考虑第3.4.3小节“人口预报”案例，用前差公式计算美国人口的年增长率，假设人口年增长率是人口数量的二次函数，重新建模、求解和分析.习题 41. 请估算第4.1.6小节“排污量的估计”案例中氨氮污染物的排放量.2. 继续考虑第4.1.7小节“饮酒驾车”案例，大李在喝了3瓶啤酒后多长时间内驾车就会违反新的国家标准？分别在以下两种情况下回答：(1) 酒是在很短时间内喝的；(2) 酒是在较长一段时间（比如2小时）内喝的.3. 继续考虑第3.4.2小节“酵母培养物的增长”案例，建立微分方程模型，模拟酵母培养物的增长.习题 62. 13名儿童参加了一项睡眠时间（分钟）与年龄（岁）关系的调查，表6.18中的睡眠时间是根据连续3天记录的每天睡眠时间的平均值得到的. 请建立和求解回归模型，解释得到的结果，给出10岁儿童的平均睡眠时间及预测区间.3. 水的沸点与大气压强有密切关系，表6.19中包含了17次试验中所测得的水的沸点（华氏温度）和大气压强（水银英寸），请建立回归模型估计沸点和压强之间的关系，并给出当沸点为201.5F 时压强的预测值及预测区间.习 题 71. 对于不允许缺货的确定性静态库存模型，做灵敏度分析，讨论参数1p 、2p 和r 的微小变化对最优订货策略的影响.2. 某配件厂为装配线生产若干种部件. 每次轮换生产不同的部件时，因更换设备要付生产准备费（与生产数量无关）. 同一部件的产量大于需求时，因积压资金、占用仓库要付库存费. 今已知某一部件的日需求量100件，生产准备费5000元，库存费每日每件1元. 如果生产能力远大于需求，并且不允许出现缺货，请制定最优生产计划.3. 某商场把销售所剩的空纸皮箱压缩并打成包准备回收，每天能产生5包，在商场后院存放的费用是每包每天10元. 另一家公司负责将这些纸包运送到回收站，要收取固定费用1000元租装卸车，外加运输费每包100元. 请制定运送纸包到回收站的最优策略.6. 继续考虑例7.2.1，约束条件保持不变，将每吨内、外墙涂料的利润分别修改为5千元和4千元，请分别用图解法和单纯形法求解.。

基于matlab求解对流弥散衰减方程文章标题：基于Matlab求解对流弥散衰减方程概述：在科学研究、工程设计和环境监测等领域，对流弥散衰减方程是一个常用的数学模型。

它描述了物质在流体中的输运过程，并考虑了对流、弥散和衰减等因素。

本文将介绍如何使用Matlab软件来求解对流弥散衰减方程，并探讨其应用和优化方法。

在阅读本文之前，建议读者对微分方程、数值解法和Matlab编程有基本的了解。

一、对流弥散衰减方程的数学表达式对流弥散衰减方程描述了物质浓度或其它相关物理量随时间和空间的变化规律。

一般形式的对流弥散衰减方程可以表示为：\[\frac{{\partial C}}{{\partial t}} = D\frac{{\partial^2 C}}{{\partialx^2}} - v\frac{{\partial C}}{{\partial x}} - kC\]其中，\(C\)表示物质浓度，\(t\)表示时间，\(x\)表示空间位置，\(D\)表示弥散系数，\(v\)表示流速，\(k\)表示衰减系数。

该方程描述了物质浓度随时间和空间的变化，分别受到弥散、对流和衰减的影响。

二、使用Matlab求解对流弥散衰减方程的步骤1. 建立数值模型在使用Matlab求解对流弥散衰减方程之前，首先要建立数值模型。

根据实际问题确定边界条件、初值条件和方程的参数。

2. 离散化方程由于对流弥散衰减方程是一个偏微分方程，需要将其离散化为差分方程。

可以使用有限差分方法或有限元方法进行离散化。

3. 制定求解策略根据离散化的差分方程，选择合适的数值解法进行求解。

常用的数值解法包括显式方法、隐式方法和Crank-Nicolson方法等。

4. 编写Matlab程序根据求解策略，编写Matlab程序来求解对流弥散衰减方程。

利用Matlab的矩阵运算和数值计算函数，可以快速实现数值求解。

5. 求解方程并分析结果使用编写好的Matlab程序，对对流弥散衰减方程进行数值求解，并得到数值解。

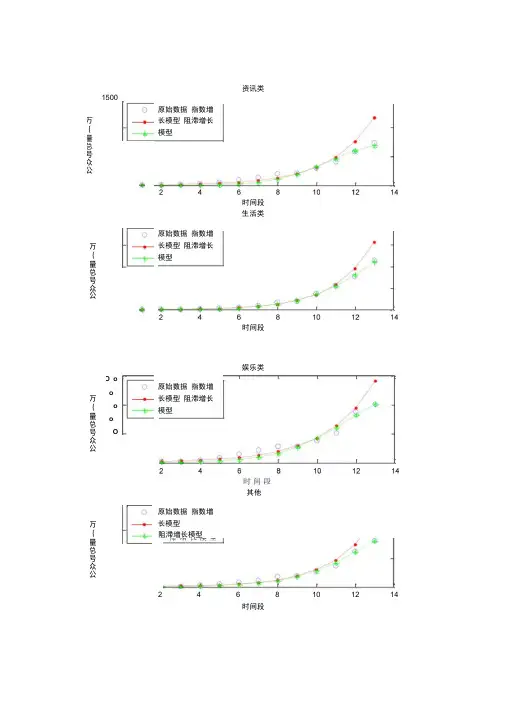
资讯类时间段原始数据指数增长模型阻滞增长模型1500万{量总号众公生活类时间段原始数据指数增长模型阻滞增长模型万{量总号众公娱乐类原始数据指数增长模型阻滞增长模型其他ooOooO321阻滞增长模型2 4 6810 12 14时间段原始数据指数增长模型万{量总号众公万{量总号众公代码：t=1:13;x=[,,,,,,,,,,,,];c=[,,,,,,,,,,,,];d=[,,,,,,,,,,,,];e=[,,,,,,,,,,,,]; %指数增长模型y=log(x);cc=log(c);dd=log(d);ee=log(e);a=polyfit(t,y,1);h= polyfit(t,cc,1); i= polyfit(t,dd,1); k= polyfit(t,ee,1); r=a(1); r2=h(1);r3=i(1);r4=k(1);x0=exp(a(2)); x1=x0*exp(r*t);c0=exp(h(2));c1=c0*exp(r2*t);d0=exp(i(2));d1=d0*exp(r3*t);e0=exp(k(2));e1=e0*exp(r4*t);%阻滞增长模型f=@(a,t) a(1)./(1+(a(1)/x(1)-1)*exp(-a(2)*(t-t(1))));f=@(h,t) h(1)./(1+(h(1)/c(1)-1)*exp(-h(2)*(t-t(1))));f=@(i,t) i(1)./(1+(i(1)/d(1)-1)*exp(-i(2)*(t-t(1))));f=@(k,t) k(1)./(1+(k(1)/e(1)-1)*exp(-k(2)*(t-t(1))));a=lsqcurvefit(f,[800 1],t,x);h=lsqcurvefit(f,[800 1],t,c);i=lsqcurvefit(f,[800 1],t,d);k=lsqcurvefit(f,[800 1],t,e);figure(1);subplot(2,1,1);plot(t,x,'o',t,x1,'r:.');x2=f(a,t);plot(t,x,'o',t,x1,'r:.',t,x2,'g*--')legend(' 原始数据',' 指数增长模型',' 阻滞增长模型',2) xlabel 时间段ylabel 公众号总量(万)title(' 资讯类');figure(1)subplot(2,1,2);plot(t,c,'o',t,c1,'r:.');c2=f(h,t);plot(t,c,'o',t,c1,'r:.',t,c2,'g*--')legend(' 原始数据',' 指数增长模型',' 阻滞增长模型',2) xlabel 时间段ylabel 公众号总量(万)title(' 生活类');figure(2) subplot(2,1,1);plot(t,d,'o',t,d1,'r:.');d2=f(i,t);plot(t,d,'o',t,d1,'r:.',t,d2,'g*--')legend(' 原始数据',' 指数增长模型',' 阻滞增长模型',2)xlabel 时间段ylabel 公众号总量(万)title(' 娱乐类');figure(2)subplot(2,1,2);plot(t,e,'o',t,e1,'r:.');e2=f(k,t);plot(t,e,'o',t,e1,'r:.',t,e2,'g*--')legend(' 原始数据',' 指数增长模型',' 阻滞增长模型',2) xlabel 时间段ylabel 公众号总量(万)title(' 其他');(jeneral model;cf_ (st) = Ml/ (l-HjO*erp (-teO* 1)))'with 9&9S conf i den 匚E bounds);龙254 (11. 73, 4497)164 (66. 7L 26L 1) 0. 1S2 (lO. 1411, 0-2228)ell =General model;elf _(K ) = 8.1/ (1+bl *B3tp (-kl* (x —1)))Coefficient 3■ (with 9&W confidence bourids)al =1FS. 1 (129.鸟 1S6.4) bl = 47. 52 (12. 53, 62.36) kl 二0.2451(0.1779, 0.3143)k(x 1)Coefficient saO =bO -kO =General mode1:c2f_ bt) = a2/ (l+b2*exp (-k2* Cx~ l)i )95% confidence bounds):(45.75, 1577)(356-3, 986^7)(Q. 190^ 0.2724)General mode1:c3f _(x) = aS/(l+b3*exp(j k3+(x_ i)))Coftff icierrt r (urith 95飯conf idtriee bounds):a3 = 1365(-5500, 82旳)b3 =301. 5(-971. 157E)=0.166(0.08979, 0.2423)c4f_ =General model:c4f_ Cx)=a4/ (l+"b4*exp (-k4w (K T j ) jCoefficients (vilh95馬tcunds):制= 2.459&+06(-2. 293^+10, 2.294&<10)b4 二9. S88e+D5(-9.. 22e-H)9, 9. 222e-tO9)k4 =0. 174(0. 1157, D. 2314)各个领域公众号对比图资讯类生活类C?f00700600500400300200T—4^5程序代码：x=[1:2:26]';------ 公众号总量娱乐类其他类Coefficient s (応th a2 =811.4b2 = 6710. 2313b=[,,,,,,,,,,,,]';c=[,,,,,,,,,,,,]';d=[,,,,,,,,,,,,]';e=[,,,,,,,,,,,,]';st_ = [500 30 ];ft_ = fittype('a0/(1+b0*exp(-k0*(x-1)))',...'dependent',{'y'},'independent',{'x'},...'coefficients',{'a0', 'b0','k0'});cf_ = fit(x,y,ft_,'Startpoint',st_)plot(cf_,'fit',;hold on,plot(x,y,'ro') f1t_ = fittype('a1/(1+b1*exp(-k1*(x-1)))',...'dependent',{'b'},'independent',{'x'},...'coefficients',{'a1', 'b1','k1'});c1f_ = fit(x,b,f1t_,'Startpoint',st_)plot(c1f_,'fit',;hold on,plot(x,b,'g*') f2t_ = fittype('a2/(1+b2*exp(-k2*(x-1)))',...'dependent',{'c'},'independent',{'x'},...'coefficients',{'a2', 'b2','k2'});c2f_ = fit(x,c,f2t_,'Startpoint',st_)plot(c2f_,'fit',;hold on,plot(x,c,'b+') f3t_ = fittype('a3/(1+b3*exp(-k3*(x-1)))',...'dependent',{'d'},'independent',{'x'},...'coefficients',{'a3', 'b3','k3'});c3f_ = fit(x,d,f3t_,'Startpoint',st_)plot(c3f_,'fit',;hold on,plot(x,d,'*') f4t_ = fittype('a4/(1+b4*exp(-k4*(x-1)))',...'dependent',{'e'},'independent',{'x'},...'coefficients',{'a4', 'b4','k4'}); c4f_ = fit(x,e,f4t_,'Startpoint',st_)plot(c4f_,'fit',;hold on,plot(x,e,'yo')。

MATLAB朴素贝叶斯模型参数一、介绍朴素贝叶斯模型是一种基于贝叶斯定理和特征条件独立假设的分类器，它在实际应用中有着广泛的用途，包括文本分类、垃圾邮件过滤、情感分析等领域。

在MATLAB中，我们可以通过调整朴素贝叶斯模型的参数来优化分类效果。

本文将介绍MATLAB中朴素贝叶斯模型的参数及其调整方法。

二、朴素贝叶斯模型参数在MATLAB中，朴素贝叶斯模型的参数包括平滑参数（smoothing）、先验概率（prior）、类条件概率模型（distribution）、特征选择（varnames）等。

下面将对这些参数逐一进行介绍。

1. 平滑参数（smoothing）平滑参数用于避免零概率，常用的平滑方法包括拉普拉斯平滑（Laplace）、里奇平滑（Ridge）、加一平滑（Add-one）等。

在MATLAB中，可以通过设定'FitMethod'参数来选择不同的平滑方法。

2. 先验概率（prior）先验概率是指在没有任何信息的情况下，各个类别的概率。

在朴素贝叶斯模型中，先验概率可以通过'Prior'参数进行调整。

在实际应用中，我们可以通过对数据集进行分析，来估计各个类别的先验概率。

3. 类条件概率模型（distribution）类条件概率模型用于描述不同类别下特征的条件概率分布。

在MATLAB中，可以通过设置'Distribution'参数来选择不同的概率分布模型，包括正态分布（normal）、多项式分布（mn）、卡方分布（kernel）等。

4. 特征选择（varnames）特征选择指的是选择参与分类的特征。

在MATLAB中，可以通过设置'PredictorNames'参数来选择不同的特征。

三、调整参数的方法在MATLAB中，可以使用朴素贝叶斯模型拟合数据，并通过交叉验证等方法来评估模型性能。

根据评估结果，我们可以调整模型的参数来优化分类效果。

阻滞增长模型（Logistic Growth Model）是一个常见的数学模型，用于描述在有限资源情况下一个种群的增长模式。

在 MATLAB 中，阻滞增长模型可以用如下代码实现：
matlab复制代码
% 定义参数
r = 1; % 增长率
K = 100; % 环境容量
y0 = 10; % 初始种群数量
% 定义时间跨度
tspan = [050];
% 定义阻滞增长模型
logistic = @(t, y) r*y*(1 - y/K);
% 使用 MATLAB 的 ODE45 解决常微分方程
[t, y] = ode45(logistic, tspan, y0);
% 画图
plot(t, y, '-');
xlabel('Time');
ylabel('Population');
title('Logistic Growth Model');
这段代码首先定义了阻滞增长模型的参数：增长率 r、环境容量 K 和初始种群数量 y0。

然后，它定义了时间跨度 tspan 和阻滞增长模型函数 logistic。

最后，它使用 MATLAB 的 ode45 函数来解决常微分方程，并使用 plot 函数画出了结果。